CONVERGENCE OF THE CRANK-NICOLSON/NEWTON SCHEME FOR NONLINEAR PARABOLIC PROBLEM∗
Xinlong FENG(冯新龙)College of Mathematics and System Sciences,Xinjiang University,Urumqi 830046,ChinaE-mail:fxlmath@xju.edu.cnYinnian HE(何银年)Center for Computational Geosciences;School of Mathematics and Statistics,Xi’an Jiaotong University,Xi’an 710049,ChinaE-mail:heyn@mail.xjtu.edu.cn
CONVERGENCE OF THE CRANK-NICOLSON/NEWTON SCHEME FOR NONLINEAR PARABOLIC PROBLEM∗
Xinlong FENG(冯新龙)
College of Mathematics and System Sciences,Xinjiang University,Urumqi 830046,China
E-mail:fxlmath@xju.edu.cn
Yinnian HE(何银年)
Center for Computational Geosciences;School of Mathematics and Statistics,Xi’an Jiaotong University,Xi’an 710049,China
E-mail:heyn@mail.xjtu.edu.cn
AbstractIn this paper,the Crank-Nicolson/Newton scheme for solving numerically secondorder nonlinear parabolic problem is proposed.The standard Galerkin finite element method based on P2conforming elements is used to the spatial discretization of the problem and the Crank-Nicolson/Newton scheme is applied to the time discretization of the resulted finite element equations.Moreover,assuming the appropriate regularity of the exact solution and the finite element solution,we obtain optimal error estimates of the fully discrete Crank-Nicolson/Newton scheme of nonlinear parabolic problem.Finally,numerical experiments are presented to show the e ffi cient performance of the proposed scheme.
Key wordsnonlinear parabolic problem;Crank-Nicolson scheme;Newton method; finite element method;optimal error estimate
2010 MR Subject Classi fi cation65N30;76M10
∗Received October 21,2014;revised March 11,2015.This work is in part supported by the Distinguished Young Scholars Fund of Xinjiang Province(2013711010),NCET-13-0988 and the NSF of China(11271313,11271298,61163027,and 11362021).
1 Introduction
In this paper,we aim to present a fully discrete Crank-Nicolson/Newton scheme for secondorder nonlinear parabolic problem.It is well-known that the Crank-Nicolson scheme is an e ffi cient scheme for solving linear and nonlinear parabolic problems since it has a second order accuracy of time step size k,see Thomée[23]and Thomée,Xu and Zhang[24]for linear parabolic problem,Douglas and Dupont[9],and Rodenkirchen[21]for the nonstationary Stokes problem and Heywood and Rannarcher[16]for the time-dependent Navier-Stokes problem.However,the Crank-Nicolson scheme will result the system of nonlinear equations when it is used to solve the nonlinear parabolic problem.To overcome this difficulty,many linearized Crank-Nicolson schemes which are of the second-order accuracy are considered,for example,see Baker[2],Heywood and Rannarcher[16],He[13]and Labovsky et al.[18]for the Crank-Nicolson extrapolation scheme or the stabilized Crank-Nicolson extrapolation scheme of the Navier-Stokes problem,Marion and Temam[19],Tone[25],Johnston and Liu[17]and He and Sun[14]for the Crank-Nicolson/Adams-Bashforth scheme of the Navier-Stokes problem.
Moreover,the Newton method or its modi fied methods,e.g.,the inexact Newton method and the quasi-Newton methods are some classical linearized algorithms for solving the system of nonlinear equations which were considered by Dembo,Eisenstat and Steihaug in[6]and Dennis and Moré in[7,8].These methods are attractive because it converges rapidly from any sufficiently good initial data.Hence,the Newton method is also used to find the finite element approximate solution of nonlinear elliptic PDEs.For the finite element solution of the mildly nonlinear elliptic PDEs,the Newton method was considered by many authors such as Douglas and Dupont in[10],Bank and Rose in[3]and Xu in[27].Also,the two-level method based on the Newton method for the general nonlinear elliptic PDEs was considered by Xu in[28].Recently,the Newton method was used to solve the 2D steady Navier-Stokes equations by He and Li in[15].And the two-level multiscale finite element methods with the simple and Newton schemes also was presented respectively for the steady Navier-Stokes problem by Wen et al.in[26].
Hence,in this paper we shall consider a new linearized Crank-Nicolson scheme which combines the Crank-Nicolson scheme with the Newton method for solving the nonlinear finite element equation related to the nonlinear parabolic problem.Here the spatial discretization of the nonlinear parabolic problem is based on the P2conforming elements;and time discretization of the nonlinear finite element equation is made by the Crank-Nicolson/Newton scheme.Finally,the convergence rate of the fully discrete Crank-Nicolson/Newton scheme are provided to justify the e ffi ciency of these algorithms,where the L2-convergence rate of the error is of third order in mesh size h and second order in time step size.
This paper is organized as follows.In Section 2 the finite element approximation of the linear parabolic problem is considered and the error estimates in mesh size h of the semi-discrete fi nite element solution are given.In Section 3 the finite element approximation of the nonlinear parabolic problem is considered and optimal error estimates in mesh h of the semi-discrete finite element solution are given.In Section 4 the fully discrete Crank-Nicolson/Newton scheme of the nonlinear parabolic problem are designed and optimal error estimates of the fully discrete finite element solution are provided.In Section 5 numerical experiments are conducted to observe the convergence and stability behavior of the proposed scheme.
2 Finite Element Method for the Linear Parabolic Problem
In this section,we shall consider some results of finite element discretizations for secondorder linear parabolic problem.These results are useful for the further analysis of nonlinear parabolic problem.

Let Ω be a convex domain in plane.For m≥0 and p≥1,we introduce the standard Sobolev space Wm,p(Ω)with a norm‖·‖m,pand a semi-norm|·|m,pgiven byFor p=2,we denote Hm(Ω)=Wm,2(Ω)andThe space X′=W−1,2(Ω)is the dual space of X.Also,we denote the scalar product and norm on L2(Ω)=W0,2(Ω)or L2(Ω)2=(W0,2(Ω))2by(·,·)and‖·‖0,2.For some detail case of the Sobolev spaces,the reader can refer to Adams[1].
Let α=α(x),β=β(x)and γ=γ(x)(with the ranges in R2×2,R2and R1,respectively)
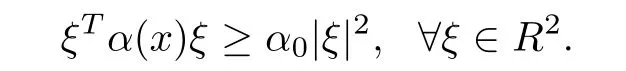
We shall study a linear parabolic problem firstly

with

Our basic assumption is that the nonsymmetric linear operatoris an isomorphism for all t∈[0,T].A simple sufficient condition for this assumption to be satis fied is thatAn application of the open-mapping theorem yields
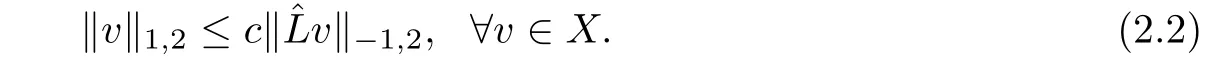
Throughout this paper,we shall use the letters C or c(with or without subscripts)to denote a general positive constant depending on the coeffi cients of the differential operator we study and the domain Ω,which can take the different value at its different occurrences.For the convenience,we shall often use a notation φ(t)to denote a function φ(x,t)in space variable x and time variable t in this paper.
Corresponding to the linear operator,we de fi ne a bilinear form,for u,v∈X,as

Now,we consider the following boundary value problem:given f∈H−1(Ω)and find u(t)∈X for all t∈(0,T]such that

with u(0)=u0(x).
We shall recall the following well-known regularity result(see Grisvard[12]).

where cqis a positive constant,depending on q,the coeffi cients ofand the domain Ω.
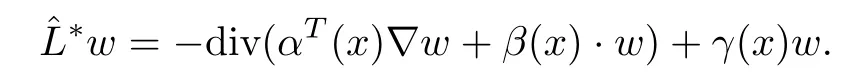
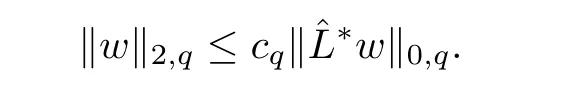
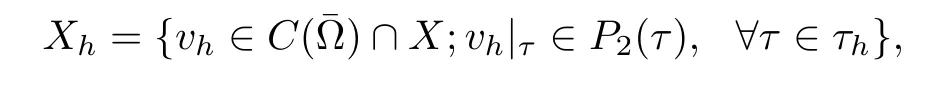
where P2(τ)is the space of polynomial of degree not greater than 2.It is well-known[5]that Xhsatisfies the following approximate property:

for all v∈Wk,p∩X with 2≤k≤3 and 1≤p≤q≤∞.Also,the following inverse inequalities in Xh

hold(see[5]).
It follows from the construction of Xhthat the standard finite element approximation of(2.3)is to find uh(t)∈Xhsuch that for all t∈(0,T],
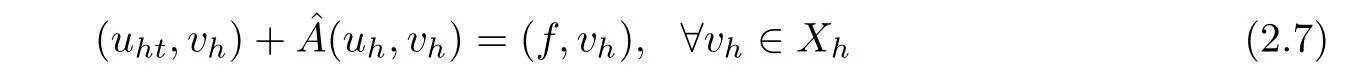
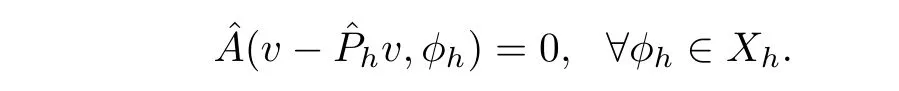
It is well known[20,28]that
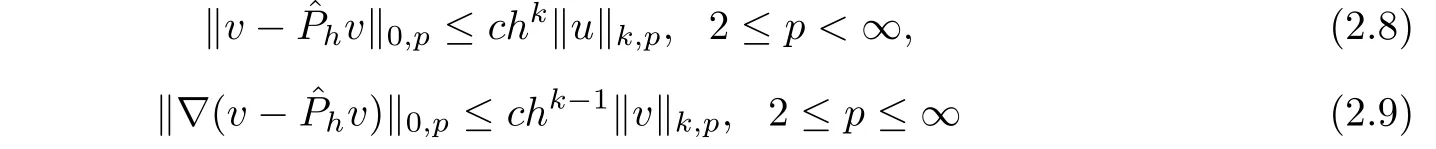
for all v∈Wk,p(Ω)and 2≤k≤3.
Moreover,by(2.5),(2.8)-(2.9)and the duality argument,we can deduce the following negative norm estimate of v−hv:
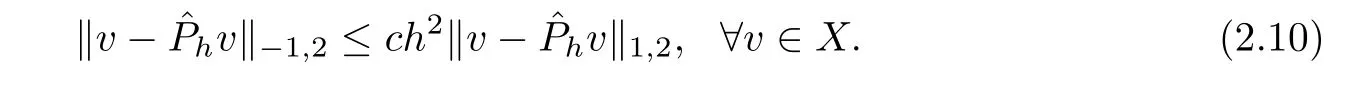
To see above estimate,we can consider an auxiliary problem:find w∈X such that

By the well-known regularity estimates(cf.[11]):

Thus,
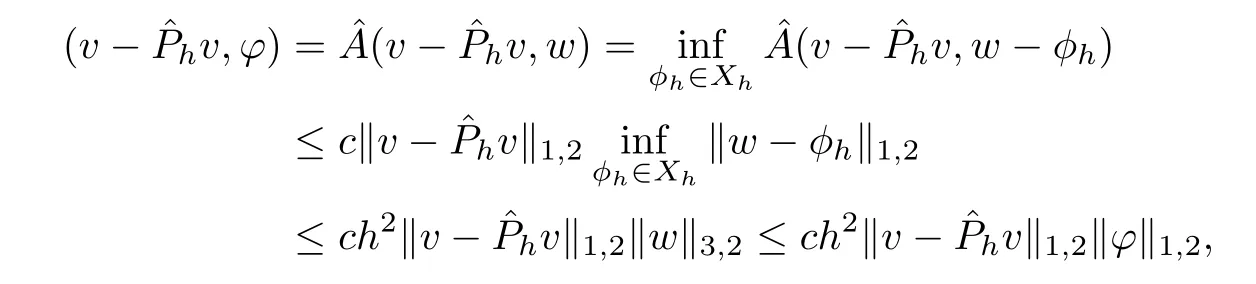
(2.10)then follows.
Moreover,by the assumption ofand the Poincare inequality
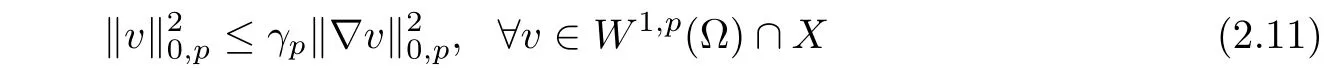
for the Poincare constant γp,we have that there exist three constants c0,c1and c2such that

and
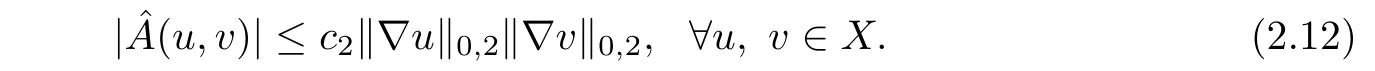
For the first inequality of(2.12),the reader can refer to Schatz[22]for some details.
Also,we need the following Gronwall lemma[4].
Lemma 2.2Let x(t),y(t)and g(t)be three nonnegative functions for t≥t0and C0is a nonnegative constant such that

Then there holds
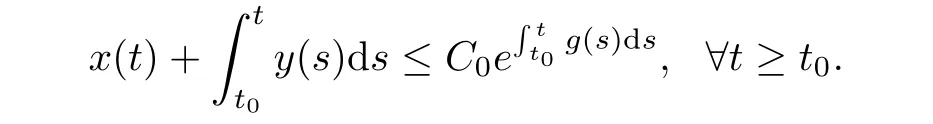
For the convenience,we shall often use u(t)and uh(t)to denote u(x,t)and uh(x,t)in this paper.
With the above statements,we can deduce the following error estimates for the finite element solution uhto the projection solution
Lemma 2.3If h is sufficiently small and ut∈L2(0,T;W2,2(Ω)∩X),then


In particular,taking vh=e∈Xhin(2.12)and using(2.13)and the Young inequality,we obtain

Integrating(2.14)from 0 to t and using(2.8),(2.10)and Lemma 2.2,the proof of Lemma 2.3 is completed.
Combining Lemma 2.3 with(2.8),we obtain the following error bounds of uhto u.
Theorem 2.4Assume that u and uhare the solutions of(2.3)and(2.7),respectively,and u satisfies
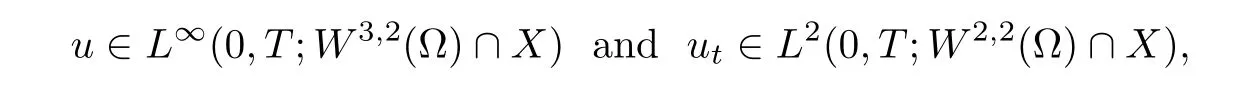
then

3 Finite Element Method for the Nonlinear Parabolic Problem
This section is to discuss the finite element method for the nonlinear parabolic problem.We consider the second-order quasi-linear parabolic problem

with


The linearized operator L at w(namely,the Fréchet derivative of L at w)is then given by
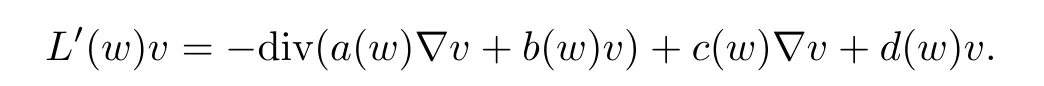
Our basic assumptions are,first of all,for the solution of(3.1),
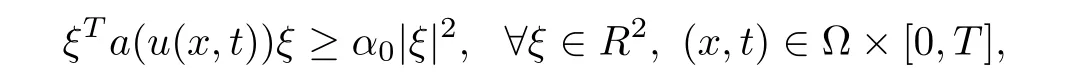
and,second,L′(u(·,t)):X→X′is an isomorphism for all t∈[0,T].
Setting
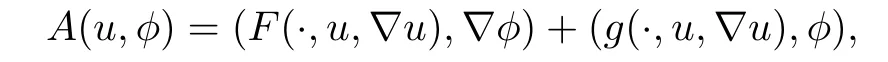
then the solution u(t)∈X of(3.1)satisfies that for all t∈(0,T],

with u(0)=u0(x).The standard finite element approximation of(3.1)is to finduh(t)∈Xhsuch that for all t∈(0,T],
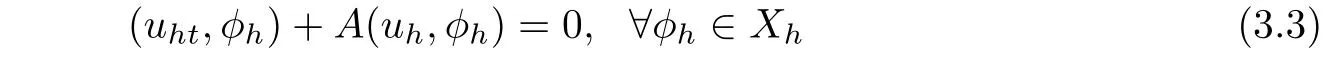
with uh(0)=hu0(x),hereh:X→Xhis de fined by

Introducing the bilinear form(induced by L′(w))

and noting the assumption of L′(u(·,t))and using the Poincare inequality,we have
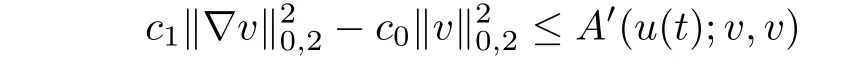
and

for all t∈[0,T].
Also,we have the following results(see[28]).
Lemma 3.1For any v,w,φ∈X,

here the remainder R satisfies,with e=v−w,1p+1q=1,p,q≥1,
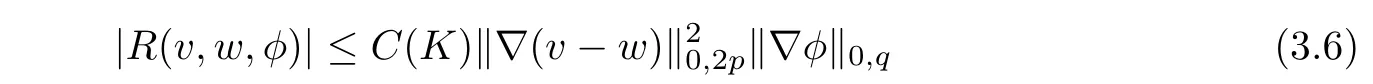
for any given K>0 and the functions v and w satisfying

where
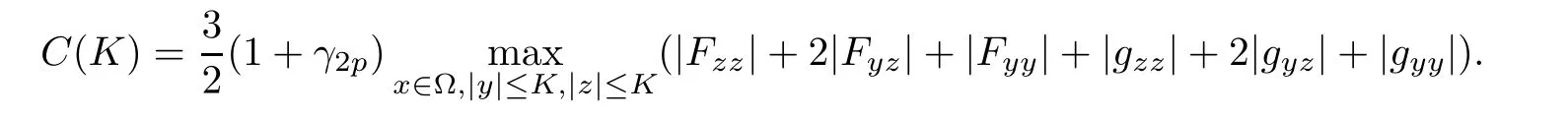
Now,we recall some error estimates for the finite element approximation uh.
Theorem 3.2Assume that u(t)∈X and uh(t)∈Xhare the solutions of(3.2)and(3.3),respectively,and

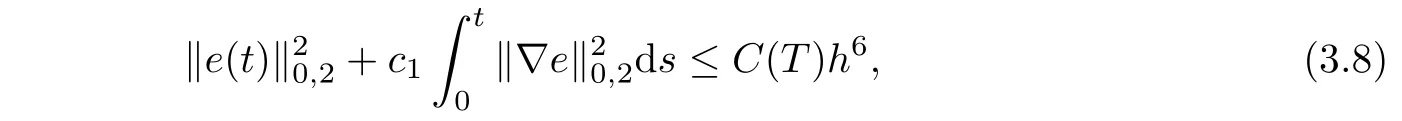

for the sufficiently small h such that

for some constant c4>0.
ProofWe assume that u and uhare the solutions of(3.2)and(3.3),respectively.Inspired by Lemma 2.3 to the error estimate for the finite element approximation of the linear parabolic problem,we give a guess that e=uh−hu satisfies(3.8).We shall give an explicit form of C(T).It follows from(2.6),(2.9)and(3.8)that if h is sufficiently small,then


where


In particular,taking φh=e∈Xhin(3.12)and using(3.4),(3.13)and the Young inequality,we obtain


Combining these estimates with(3.14)yields
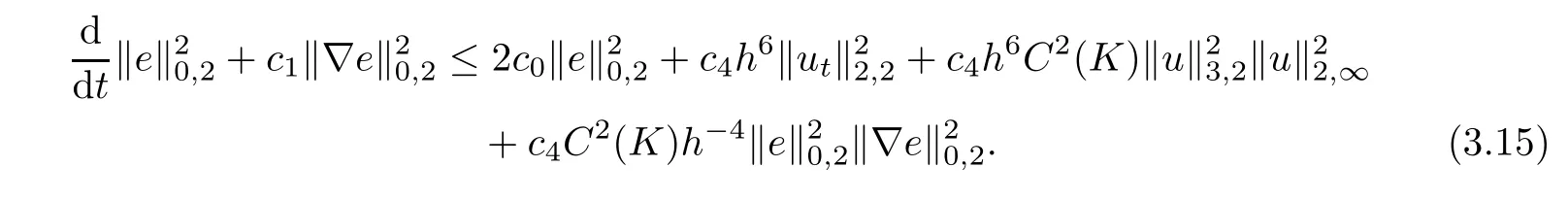
Integrating(3.15)from 0 to t and using Lemma 2.2,we obtain

In(3.16),we assume that h is su ffi cient small which satisfies(3.10).Then we deduce from(3.16)that C(T)satisfies(3.9).The proof ends.
Combining Lemma 3.2 with(2.8),we obtain the following error bounds of uhto u.
Theorem 3.3Under the assumptions of Lemma 3.2,the errors u−uhandsatisfy the following bound

4 Crank-Nicolson/Newton Scheme for Nonlinear Problem
In this section,we shall present the fully discrete Crank-Nicolson/Newton scheme based on the P2finite element for the nonlinear parabolic problem.
For a given integer number N,we setare the approximations ofrespectively,and using the Newton approximate of the nonlinear termwe obtain the following linearized equation:Then,we apply the Crank-Nicolson scheme to discrete the above Newton equation by approximatingThis results the following fully discrete numerical scheme.
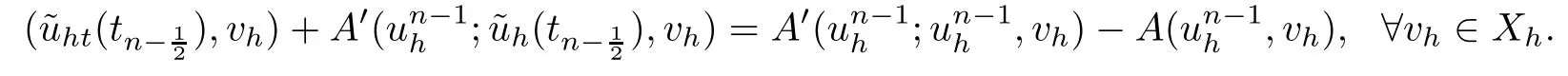
Crank-Nicolson/Newton SchemeDe fi ne the discrete solution sequence{unh}⊂Xhsuch that
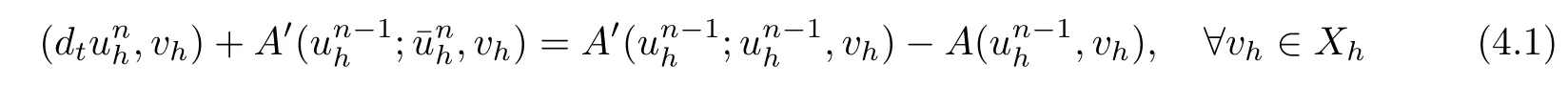
Here and after,we need to estimate A′(v;φ,ψ)−A′(w;φ,ψ)for all v,w∈W1,∝with ‖v‖1,∝≤K,‖w‖1,∝≤K and φ,ψ∈X.
Note that
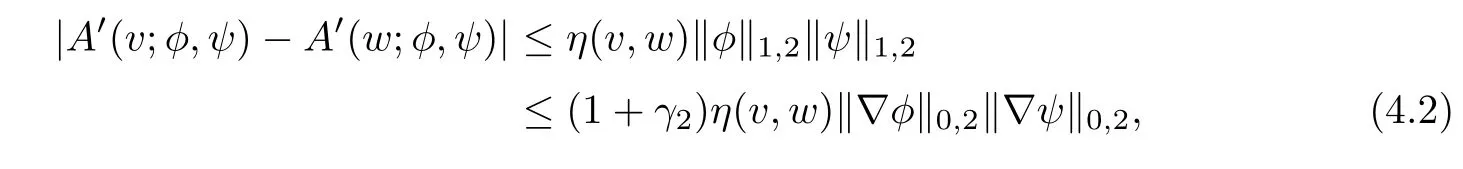
where
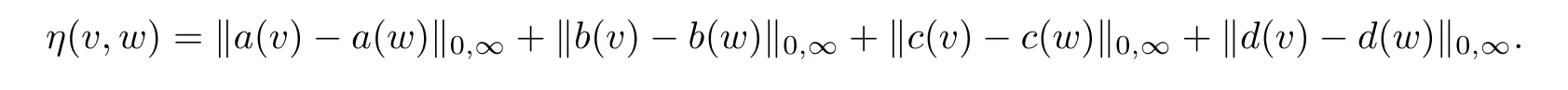
Setting

a straightforward calculation shows that
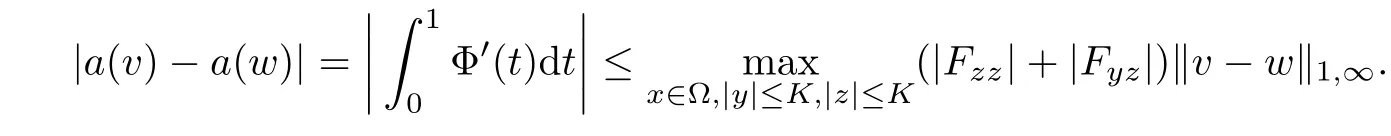
Similarly,we have

Combining these estimates with(4.2)and using(2.11)yields
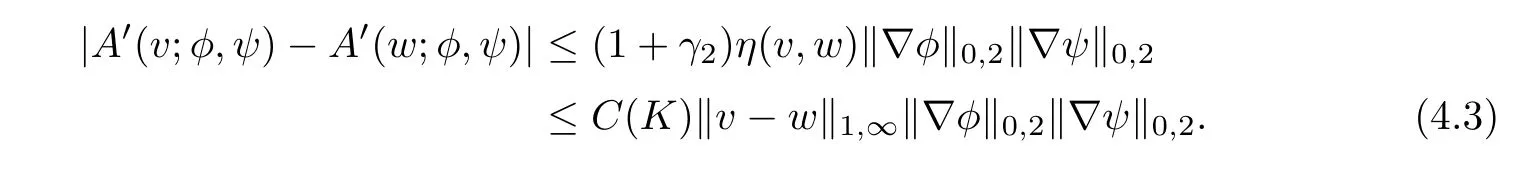
Also,we need the following discrete Gronwall lemma[16].
Lemma 4.1Let an,bnand dnare nonnegative numbers for n≥0 and C0is a nonnegative constant such that
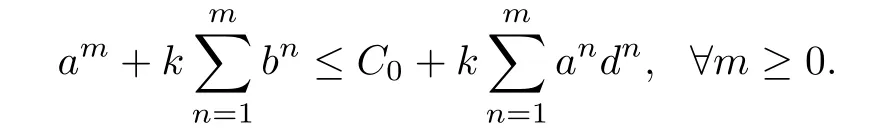
If dnk<1 for all n≥1,then there holds
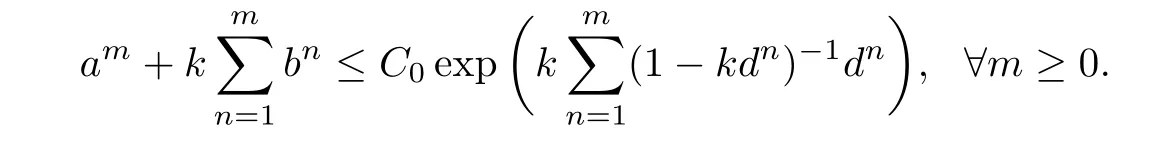
Lemma 4.2Assume that h and k is sufficiently small,u is the solution of(3.2)satisfying the assumption of Lemma 3.2 and uhis the solution of(3.3)satisfying
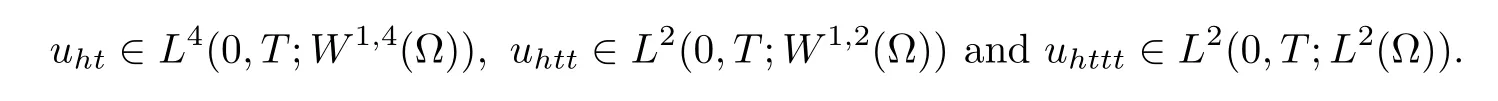
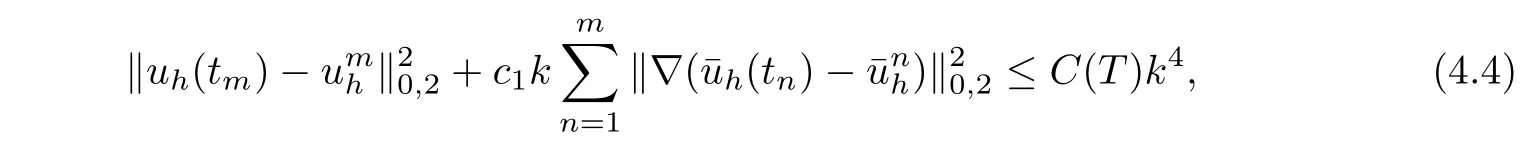
where

and
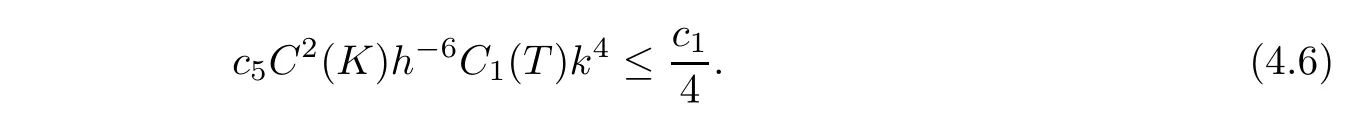
ProofNow,we shall prove(4.4)by the induction method.First,(4.4)is true for m=0.Assume that(4.4)is true for m=J−1.We need to prove(4.4)for m=J.It follows from the induction assumption and(4.6)that

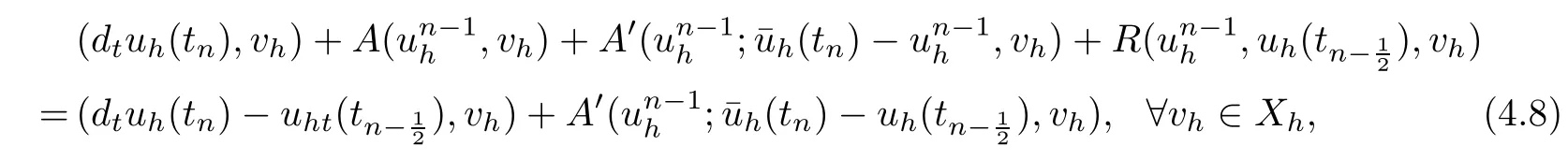
where
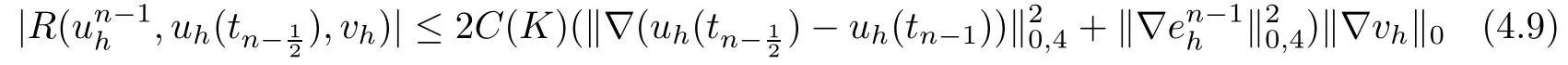
for all vh∈Xh.
It follows from(4.1)and(4.8)that

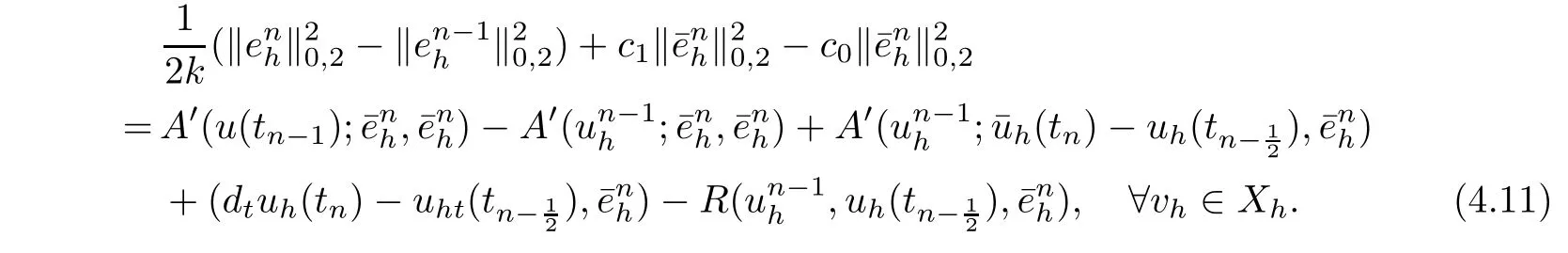
For the convenience,we denoteUsing(3.4),(4.3)and the induction assumption,we have that for sufficiently h and k,
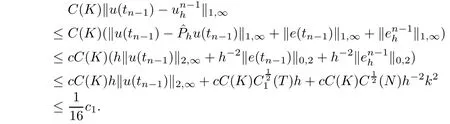
For the first two terms of the right hand side of(4.11),we have

For the third term of the right hand side of(4.11),we have
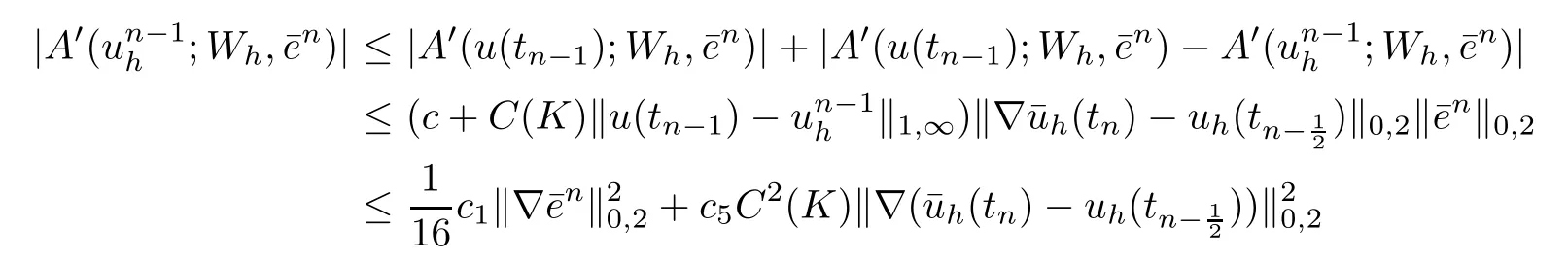
and

For the fourth term of the right hand side of(4.11),we have
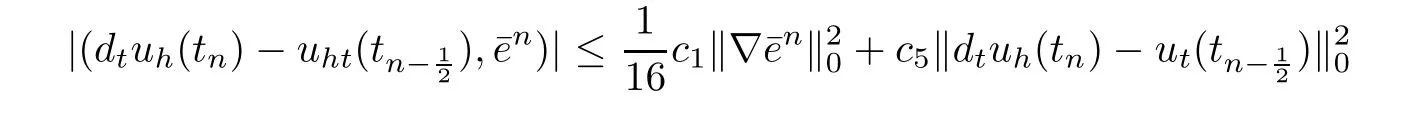
and

For the last term of the right hand side of(4.11),we also have

and
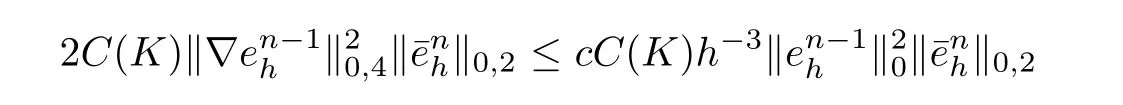

Combining these estimates with(4.11)and using(4.6)gives
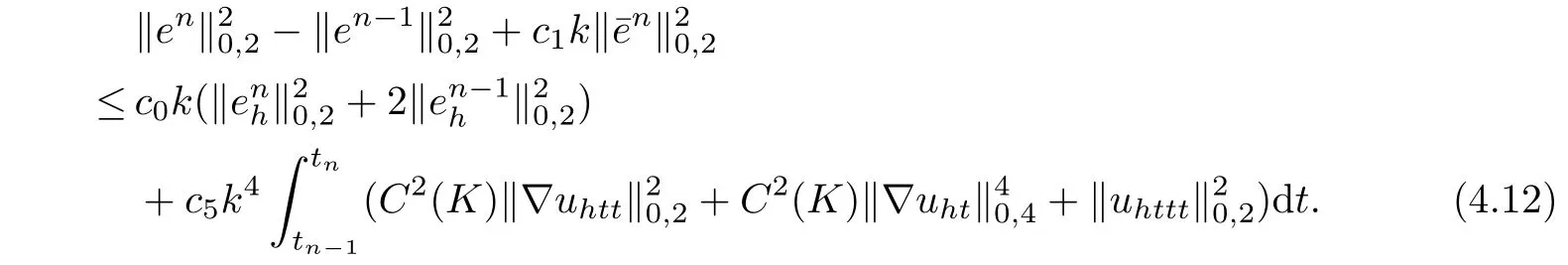
Summing(4.12)from n=1 to n=J,we obtain

Apply Lemma 4.2 to(4.13)with


The induction is completed and Lemma 4.2 is proven.
Note that combining Lemma 4.2 with Theorem 3.3 yields the following error estimate results.
Theorem 4.3Under the assumptions of Lemma 4.2,u andsatisfy the following error estimate
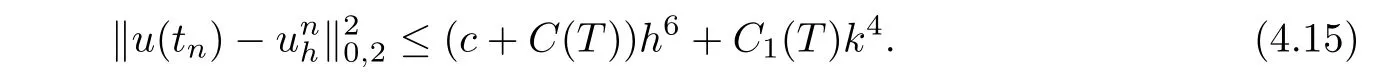
Moreover,we can also prove the existence and uniqueness of the solution sequenceif h and k is sufficiently small.Note that(4.1)can be rewritten into the following form:
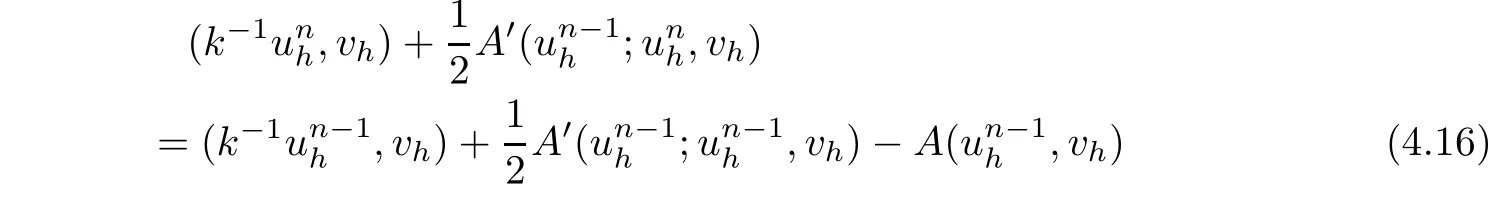
for all vh∈Xh.For a givenwe can prove that the bilinear form
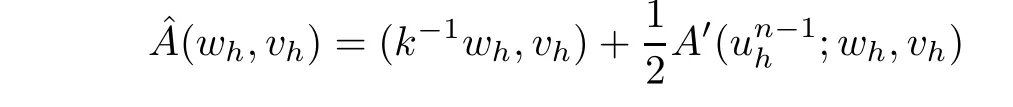
on Xh×Xhis continuous and elliptic.In fact,the previous estimates in the proof of Lemma 4.2,we have

for sufficiently small h and k.Hence,by(3.4)and(4.3),we have
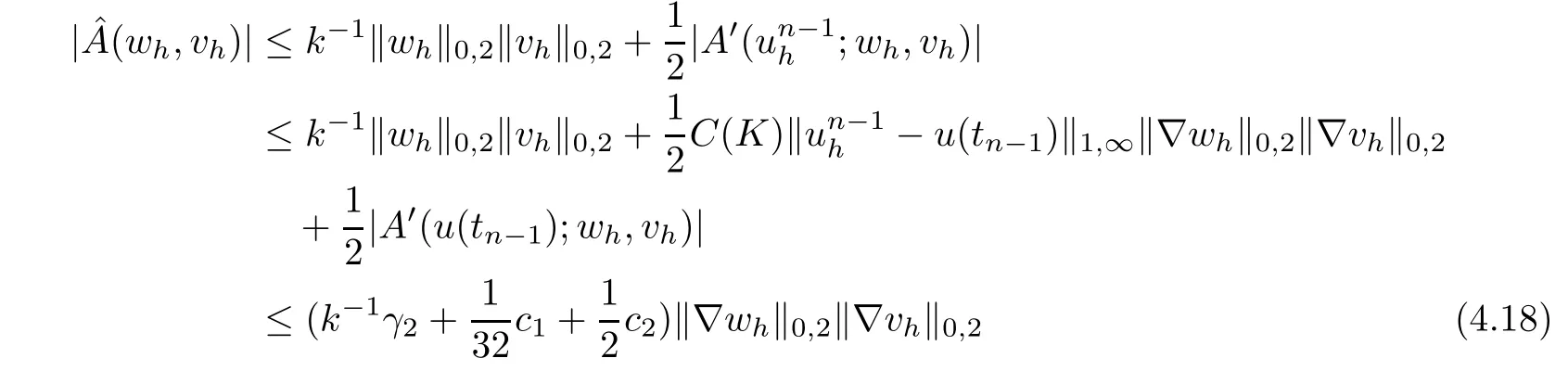
and

5 Numerical Results
In this section,we present some numerical experiments aimed at highlighting the practical performance of new scheme introduced in this paper for the numerical approximation of nonlinear parabolic equations.
5.1Example 1
For simplicity,we let Ω be the square domain[0,1]×[0,1]and consider the case where F(x,u,∇u)=u2∇u.The function g(x,u,∇u)is such that the equation has an analytical solution u(x,y,t)=sin(πx)sin(πy)exp(−t).
Using the de finition of bilinear forms,we have

and

here we use P2conforming element for spatial discretization.We consider the uniform time step k=10−5for time discretization.The time step is sufficiently small so that the spatial error dominates the computation;thus we can neglect the in fl uence of the time step size.The convergence history of the proposed scheme is listed in Table 1,which illustrate the convergenceand stability of the fully discrete scheme at T=0.1.We can see that the convergence rates are optimal.
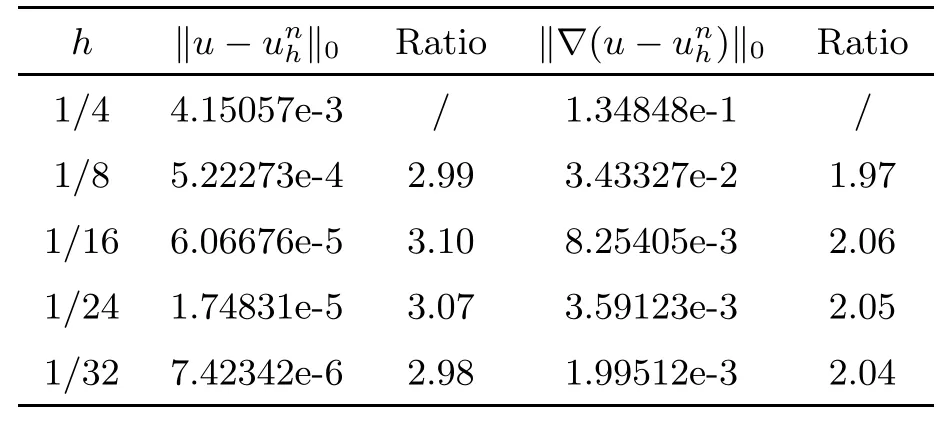
Table 1 Numerical results for spatial discretization of Example 1
5.2Example 2
Now we turn our attention to the application of new scheme to the solution of the Allen-Cahn equation with a homogeneous Dirichlet boundary condition on the unit square.The Allen-Cahn equation can be rewritten as

where the unknown function u represents an order parameter,and the nonlinear term g(u)=(u−u3)2is obtained from the standard double-well free energy potential with∈measuring the interface thickness.Here we choose∈=0.1 and take as initial condition
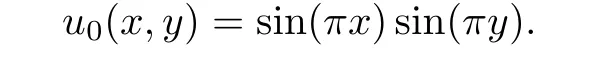
Similarly,using the de finition of bilinear forms,we have

and

In order to test the numerical accuracy,we take the numerical solution obtained using new second-order scheme with h=1/50 and k=1.0e−5 as the exact solution at T=0.1.The L2-error is shown in Table 2.It is clearly observed that the new scheme gives second-order accuracy in time.

Table 2 Numerical results for different time steps of Example 2
AcknowledgementsThe authors also thank Dr.Dongwei Gui(Cele National Station of Observation&Research for Desert-Grassland Ecosystem in Xinjiang)for his support and encouragement in this work.
References
[1]Adams R A.Sobolev Space.New York:Academic Press,1975
[2]Baker G A.Galerkin approximations for the Navier-Stokes equations.Technical Report,1976
[3]Bank R E,Rose D J.Analysis of a multilevel interative method for nonlinear finite element equations.Math Comput,1982,39:453-465
[4]Cannon J R,Ewing R E,He Y N,Lin Y P.A modi fied nonlinear Galerkin method for the viscoelastic fl uid motion equations.Inter J Eng Sci,1999,37:1643-1662
[5]Ciarlet P.The Finite Element Method for Elliptic Problems.New York:North-Holland,1978
[6]Dembo R S,Eisenstat S C,Steihaug T.Inexact Newton methods.SIAM J Numer Anal,1982,19:400-408
[7]Dennis Jr J E,Moré Jorge J.Quasi-Newton methods.Numer Math,1968,11:324-330
[8]Dennis Jr J E,Moré Jorge J.A characterization of superlinear convergence and its application to quasi-Newton methods.Math Comput,1974,28:549-560
[9]Douglas Jr J,Dupont T.Galerkin methods for parabolic equations.SIAM J Numer Anal,1970,7:575-626
[10]Douglas Jr J,Dupont T.A Galerkin method for a nonlinear Dirichlet problem.Math Comput,1975,29:689-696
[11]Gilbarg D,Trudinger N.Elliptic Partial Di ff erential Equations of Second Order.New York:Springer-Verlag,1983
[12]Grisvard P.Elliptic Problem in Nonsmooth Domains.Boston,MA:Pitman,1985
[13]He Y N.Two-level method based on finite element and Crank-Nicolson extrapolation for the time-dependent Navier-Stokes equations.SIAM J Numer Anal,2003,41:1263-1285
[14]He Y N,Sun W W.Stability and convergence of the Crank-Nicolson/Adams-Bashforth scheme for the time-dependent Navier-Stokes equations.SIAM J Numer Anal,2007,45(2):837-869
[15]He Y N,Li J.Convergence of three iterative methods based on the finite element discretization for the stationary Navier-Stokes equations.Comput.Methods Appl Mech Engrg,2009,198:1351-1359
[16]Heywood J G,Rannacher R.Finite-element approximations of the nonstationary Navier-Stokes problem,Part IV:Error estimates for second-order time discretization.SIAM J Numer Anal,1990,27:353-384
[17]Johnston H,Liu J G.Accurate,stable and e ffi cient Navier-Stokes slovers based on explicit treatment of the pressure term.J Comput Phys,2004,199:221-259
[18]Labovsky A,Layton W J,Manica C C,Neda M,Rebholz L G.The stabilized extrapolated trapezoidal finite element method for the Navier-Stokes equations.Comput Methods Appl Mech Engrg,2009,198:958-974
[19]Marion M,Temam R.Navier-Stokes Equations:Theory and Approximation.Handb.Numer.Anal.VI,Amsterdam:North-Holland,1998:503-688
[20]Rannacher R,Scott R.Some optimal error estimates for piecewise linear finite element approximation,Math Comput,1982,38:437-445
[21]Rodenkirchen J.Maximum L2-convergence rates of the Crank-Nicolson scheme to the Stokes initial value problem.SIAM J Numer Anal,2007,45:484-499
[22]Schartz A.An observation concerning Ritz-Galerkin methods with inde finite bilinear forms.Math Comput,1974,28:959-962
[23]Thomée V.Galerkin Finite Element Methods for Parabolic Problems.Berlin:Springer-Verlag,1997
[24]Thomée V,Xu J C,Zhang N Y.Superconvergence of gradient in piecewise linear finite element approximation to a parabolic problem.SIAM J Numer Anal,1989,26:553-573
[25]Tone F.Error analysis for a second scheme for the Navier-Stokes equations.Appl Numer Math,2004,50:93-119
[26]Wen J,He Y N,Wang X M,Huo M H.Two-level multiscale finite element methods for the steady Navier-Stokes problem.Acta Math Sci,2014,34B(3):960-972
[27]Xu J C.A novel two-grid method for semilinear elliptic equations.SIAM J Sci Comput 1994,15:231-237[28]Xu J C.Two-grid discretization techniques for linear and nonlinear PDEs.SIAM J Numer Anal,1996,33:1759-1777
 Acta Mathematica Scientia(English Series)2016年1期
Acta Mathematica Scientia(English Series)2016年1期
- Acta Mathematica Scientia(English Series)的其它文章
- SOME STABILITY RESULTS FOR TIMOSHENKO SYSTEMS WITH COOPERATIVE FRICTIONAL AND INFINITE-MEMORY DAMPINGS IN THE DISPLACEMENT∗
- STABILITY OF VISCOUS SHOCK WAVES FOR THE ONE-DIMENSIONAL COMPRESSIBLE NAVIER-STOKES E QUATIONS WITH DENSITY-DEPENDENT VISCOSITY∗
- STABILITY ANALYSIS OF A COMPUTER VIRUS PROPAGATION MODEL WITH ANTIDOTE IN VULNERABLE SYSTEM∗
- STABILITY OF A PREDATOR-PREY SYSTEM WITH PREY TAXIS IN A GENERAL CLASS OF FUNCTIONAL RESPONSES∗
- NONSMOOTH CRITICAL POINT THEOREMS AND ITS APPLICATIONS TO QUASILINEAR SCHRÖDINGER EQUATIONS∗
- NORMAL FAMILIES OF MEROMORPHIC FUNCTIONS WITH SHARED VALUES∗
