Calculation of propellant gas pressure by simple extended corresponding state principle
Bin XU*,San-jiu YING,Xin LIAO
School of Chemistry Engineering,Nanjing University of Science and Technology,Nanjing 210094,Jiangsu,China
Calculation of propellant gas pressure by simple extended corresponding state principle
Bin XU*,San-jiu YING,Xin LIAO
School of Chemistry Engineering,Nanjing University of Science and Technology,Nanjing 210094,Jiangsu,China
The virial equation can well describe gas state at high temperature and pressure,but the diff i culties in virial coeff i cient calculation limit the use of virial equation.Simple extended corresponding state principle (SE-CSP)is introduced in virial equation.Based on a corresponding state equation,including three characteristic parameters,an extended parameter is introduced to describe the second virial coeff i cient expressions of main products of propellant gas.The modif i ed SE-CSP second virial coeff i cient expression was extrapolated based on the virial coeff i cients experimental temperature,and the second virial coeff i cients obtained are in good agreement with the experimental data at a low temperature and the theoretical values at high temperature.The maximum pressure in the closed bomb test was calculated with modif i ed SE-CSP virial coeff i cient expressions with the calculated error of less than 2%,and the error was smaller than the result calculated with the reported values under the same calculation conditions.The modif i ed SE-CSP virial coeff i cient expression provides a convenient and eff i cient method for practical virial coeff i cient calculation without resorting to complicated molecular model design and integral calculation.
Virial coeff i cient;Simple extended corresponding state principle;High temperature;Pressure;Propellant gas
1.Introduction
The equation of state is a basic equation of interior ballistics,and the accuracy of the equation has an effect on the veracity of ballistic calculation results [1].The Nobel-Abel equation,truncated virial equation and Haar-Shenker equation have been applied successively to describe the propellant gas at high temperature and pressure [2-4].Among those equations,the virial equation is more satisfactory in describing the state of propellant gas at high temperature and pressure.But the diff i culty in acquiring the virial coeff i cient value greatly restrains the application of the virial equation.Various methods have been used to calculate the virial coeff i cients to obtain the empirical or semiempirical equations of state,such as statistic mechanics and molecular model,intermolecular interaction,equation of state for elementary gas,reciprocal space computation,neural network prediction,and other ways [4-11],whereas the diff i-culty in calculating the virial coeff i cients still exists especially in integration.
Correspondingstateprinciple (CSP)iswidelyusedinengineeringdesignandf l uidcharacteristicsprediction.Differentpuregases have a common feature,which is that their compressibility factors are nearly the same when they reach their critical points.For this common feature,when the critical pressure and the critical temperature of a gas are known,theP-V-Tcharacteristics of this pure gas could be calculated approximately without the complex integral calculation of virial coeff i cient.But the error due to the approximate calculation will accumulate with the increase in temperature and pressure.The accumulated error should not be neglected in predicting the virial coeff i cients of gas at high temperature and pressure.Therefore,the virial coeff i cients calculated by the approximation way could not be used in calculating the propellant gas at high temperature and pressure directly.Based on CSP,the main work of this paper is to introduce an extended corresponding state amendment to the virial coeff i cient expressions of the main components in propellant gas,which makes simple extended corresponding state principle (SE-CSP)available to describe the state of propellant gas at high temperature and pressure.
2.Calculation principle of virial coeff i cients
2.1.Virial equation
The virial equation was proposed by Kammerlingh-Onnes in 1901,which could be described by the reciprocal of volume power as

whereZis compressive factor;BandCare the second and the third virial coeff i cients,respectively,which only depend on temperature.
Generally,the accuracy ofZcalculation with the f i rst three terms in Eq.(1)is suff i cient [12].
The propellant gas is a mixture of several elementary gases. The second and the third virial coeff i cients of the elementary main component gases computed by using the Kay rule meet the requirement of engineering calculation accuracy.

2.2.Simple extended corresponding state principle(SE-CSP)
In CSP,if different substances have the same relative pressurePr(the ratio of pressurePand critical pressurePc)and the same relative temperatureTr(the ratio of temperatureTand critical temperatureTc),they are in a corresponding state,and their physical properties have the simple corresponding relationships.
Since this relationship with two parameters is only appropriate for simple molecules,Pitzer et al. [13]and Xiang[14]introduced acentric factorωand empirical parameterθsuccessively to amend the critical comparison factorZc,withθ= (Zc-0.291)2.The amendments make CSP f i t for describing various properties of all kinds of molecule [13,14].
After introducing parametersωandθ,CSP becomes SE-CSP,which could be expressed as

2.3.Calculation of virial coeff i cients for propellant gas
The modif i ed expressions forBr(0)(Tr)andBr(1)(Tr)in Eq.(4)are shown in Ref. [15]

Some studies have shown that the estimate accuracy ofBin Eq. (4)is satisfactory forTr<0.75,whereas the estimate accuracy becomes more and more weak with the increase inTr.The temperature range of propellant gas greatly exceedsTr=0.75. Therefore,SE-CSP like Eq. (4)should be revised before it is used to calculate the virial coeff i cients of propellant gas.
The main components of propellant gas are N2,H2,CO,H2O and CO2.Due to the good agreement between experimental data [16]and the calculated data by the second virial coeff i cient equation of CO2proposed in Ref. [17]and the precise second virial coeff i cient equation of H2O proposed in Ref. [18],only the amended expressions for CO,H2and N2are required by f i tting their experimental data [16].The expressions obtained are

3.Applied results and analysis
The second virial coeff i cients of CO,H2and N2calculated by the revised SE-CSP expression were compared with their experimental data and other calculated values from different theories.The comparative results are shown in Figs.1-3,respectively.It can be seen obviously that the values calculated by the revised SE-CSP expression have satisfactory accuracy and are in good agreement with the experimental data [16]at low temperature,and also agree well with the calculated values in Ref. [5,6]at high temperature.
When the virial coeff i cients of propellant gas at high temperature and pressure are calculated,the second virial coeff icients of CO,H2and N2can be obtained by Eqs.(4)~ (6);the second virial coeff i cients of H2O and CO2can be obtained by Eq.(7)[17]and Eq.(8)[18];the third virial coeff i cients of the f i ve elementary gases can be obtained by Eqs. (9)~ (10)and Table 1 [19].
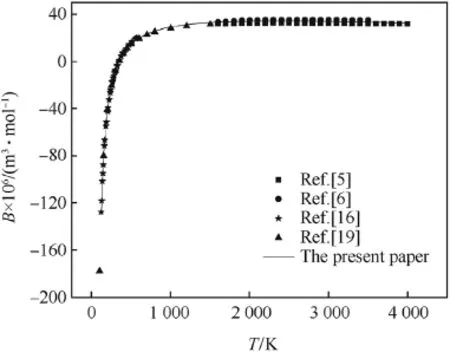
Fig.1.The second virial coeff i cients of CO.
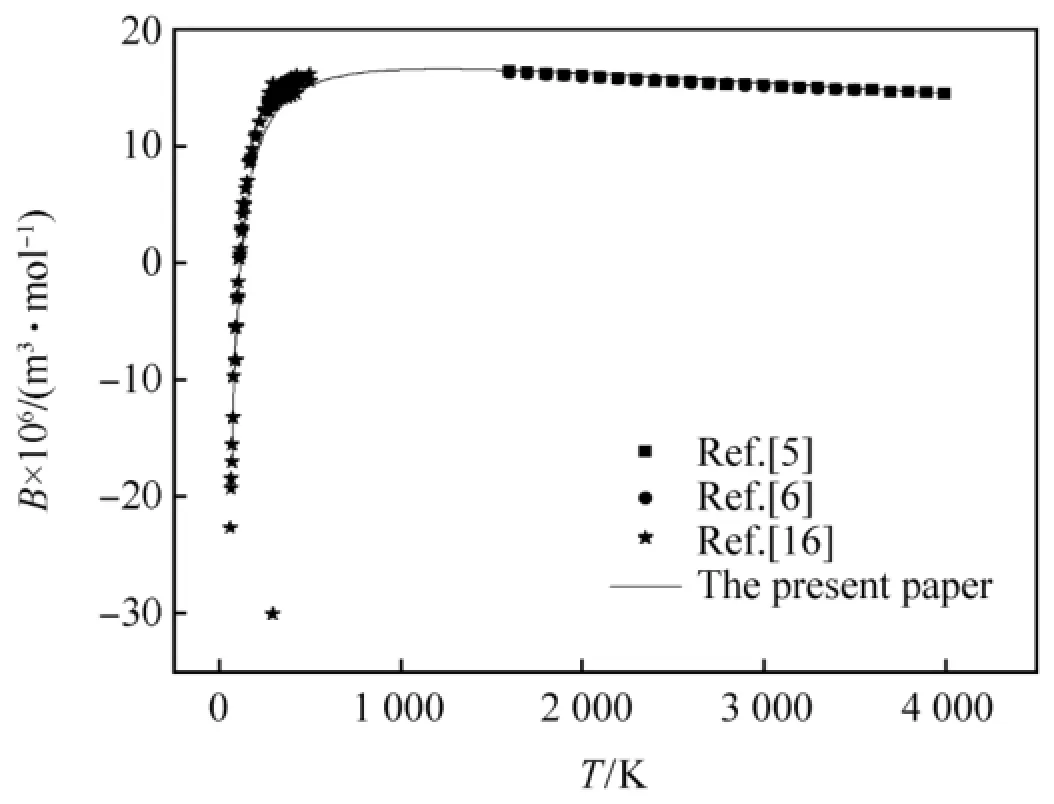
Fig.2.The second virial coeff i cients of H2.

Fig.3.The second virial coeff i cients of N2.

Table 1aij.

Although an error will be brought by using the revised third virial coeff i cient CSP equations to calculate in the third virial coeff i cient at a higher temperature,the effect of extrapolation error on the maximum pressure of the propellant gas could be ignored at such a high temperature.The second and the third virial coeff i cients of the propellant gas can be obtained by calculating the second and the third virial coeff i cients of the main component elementary gases according to Eqs.(2)~ (3),and approximately taking other small component gases as ideal gases of whichBandCare zero.Then the comparative factorZof propellant gas can be calculated.Finally,the maximum pressure of the propellant gas can be calculated by the equationpV=nZRT.
Table 2 lists the maximum pressures of closed bomb tests of a gun propellant,whose formula is C24.86H32.27O33.46N9.54,under different loading conditions.The maximum pressures calculated by different theoretical virial coeff i cients calculation methods are also listed in Table 2.These theoretical virial coeff i cients calculation methods include the revised SE-CSP virial coeff i cient expression proposed in this article,the function of a simplif i ed intermolecular force model[5]and a polarity modif i ed function based on Lennard-Jones (6-12)potential function [6].The calculations are completed under the sameconditions,such as gas composition,content of elementary component gas,explosive temperature,and other component gasses as ideal gasses except the main component gasses and so on.The experimental results in Table 2 were corrected with heat loss,and the inf l uence of ignition powder on pressure was eliminated.

Table 2Comparison of closed bomb test results and calculation results under different loading conditions.
From Table 2 it can be seen that the maximum pressure values calculated through the revised SE-CSP expression are closer to the experimental results at different loading conditions compared to the values calculated in Refs.[5,6],and the calculated errors from modif i ed SE-CSP are obviously smaller than those from the other methods with the increase in loading density.The comparative results indicate that the revised SE-CSP equation is suitable for maximum pressure calculation of propellant gas at high temperature and pressure,and its calculation accuracy is higher than those in Refs.[5,6].All the pressures calculated by the three methods in Table 2 are lower than the experimental values,and the calculated errors present a slightly increasing trend with the increase in loading density. This phenomenon is probably caused by the approximation calculation,in which the main component gases are taken as real gases,and the small quantity of other dissociated gases are taken as ideal gases.This approximation leads to the result that the calculated value is lower than the experimental data.When the loading density increases,the degree of dissociation grows higher.If the dissociated gases are taken as ideal gasses at that time,the error brought by this approximation grows.But this error is still in the acceptable range in engineering calculation. Therefore,some amendments,such as managing dissociated gas components,could be made to improve the pressure calculation accuracy of propellant gas in calculation.
4.Conclusion
For the limited temperature range of the simple extended corresponding state principle (SE-CSP)and the diff i culty in calculating the virial coeff i cients,the second virial coeff i cient SE-CSP expressions for the main component gases of propellant gas were amended by f i tting and extrapolating the corresponding experimental data of the gases.The amendment in the present paper makes the SE-CSP expressions suitable for calculating the main component gases of propellant gas at high temperature and pressure.The second virial coeff i cients calculated by the revised SE-CSP expressions are in good agreement with the experimental data at low temperature.Then these revised SE-CSP expressions are extrapolated;the second virial coeff i cients calculated by these extrapolated expressions agree with the values in Refs.[5,6]at high temperature.The extrapolated revised SE-CSP virial expressions were used to calculate the maximum pressure of propellant gas in constant volume. The calculated error presented in the paper is smaller than those in Refs. [5,6],which indicates that the extrapolated revised SE-CSP virial expressions are appropriate for the maximum pressure calculation of propellant gas in constant volume at high temperature and pressure,and have better calculation accuracy.The revised SE-CSP expressions,which avoid establishing the complicated molecular model for virial coeff i cient calculation,provide a simple way to calculate the virial coeff icient of propellant gas at high temperature and pressure,and have practical signif i cance in theoretical calculation.
[1]Yuhua Y.Research on State Equation and Its Application of Propellant Gas in High Pressure[D].Nanjing:Nanjing University of Science and Technology;1988 [in Chinese].
[2]Xishen X,Wanji Z.Theoretical guidance on practical state equation. Beijing:Science Press;1986 [in Chinese].
[3]Krier H,Summerf i ed M,editors.Interior ballistics of guns.Beijing:National Defense Industry Press;1985 [in Chinese].
[4]Freedman E.BLAKE-A thermodynamics code based on TIGER:Users guide and manual.Technical report,1982,ARBRL-TR-02411.
[5]Interior ballistics [Corner J,wrote,Tingyu B,Wenjian Q,trans.].Beijing:National Defence Industry Press;1983 [in Chinese].
[6]Volk F,Bothelt H.Application of the virial equation of state in calculating interior ballistics quantities.Propell Explos Pyrot 1976;1:7-14.
[7]Powell EG,Wilmet G,Haar L,Klein M.Equation of state and thermodynamic data for interior ballistics calculations.Progress in astronautics and aeronautics,vol.66.AIAA;1979.p.325-48.
[8]Costantino M,Ornellas D.The experimental high pressure equation of state of a very fast burning gun propellant.JANNAF Combustion Mtg,Laurel.Maryland;1984.
[9]Bonneville R.Asymptotic expression of the virial coeff i cients for hard sphere systems.Fluid Phase Equilib 2015;397:111-16.
[10]Mamedov BA,Somuncu E.Analytical treatment of second virial coeff i cient over Lennard-Jones(2n-n)potential and its application to molecular systems.J Mol Struct 2014;1068:164-9.
[11]Oreški S.Comparison of neural network and empirical methods for prediction of second virial coeff i cients for gases.Proc Eng 2012;42:303-12.
[12]Zeshan W,Weidong H,Fuming X.Design principles and technology of charge.Beijing:Beijing University of Science and Technology Press;2006 [in Chinese].
[13]Pitzer KS,Curl RF Jr.The volumetric and thermodynamic properties of f l uids.III.Empirical equation for the second virial coeff i cient.JAm Chem Soc 1957;79:2369-70.
[14]Hongwei X.Physical and chemical properties of heat f l uid:principles and applications of corresponding states.Beijing:Science Press;2003 [in Chinese].
[15]Long M,Yuanyuan D,Lei L.Correlations for second and third virial coeff i cients of pure f l uids.Fluid Phase Equilib 2004;226:109-20.
[16]Dymond JH,Marsh KN,Wilhoit RC,et al.Virial coeff i cients of pure gases.Springer-Verlag Berlin Heidelberg;2002.
[17]Harvey AH,Lemmon EW.Correlation for the second virial coeff i cient of water.J Phys Chem Ref Data 2004;33(1):369-76.
[18]Vukalovich MP,Altunin VV,Timoshenko NI.The thermodynamic properties of carbon dioxide at temperatures of 0-1000°C and pressures up to 100 bar.Translated from Atom Energy 1963;15(3):210-14
[19]Liu DX,Xiang HW.Corresponding-states correlation and prediction of third coeff i cients for a wide range of substances.Int J Thermophys 2003;24(6):1667-80.
[20]Sevast′yanov RM,Chernyavskaya RA.Virial coeff i cients of carbon monoxide,ethylene,and propylene at temperatures up to 1500 K.J Eng Phys 1990;57(4):1181-3. (Translated from Inzhenerno-Fizicheskii Zhurnal 1989;57(4):590-3).
[21]Sevast′yanov RM,Chernyavskaya RA.Virial coeff i cients of nitrogen,oxygen,and air at temperatures from 75 to 2500 K.J Eng Phys 1986;51(1):851-4. (Translated from Inzhenerno-Fizicheskii Zhurnal 1986;51(1):121-4).
Received 11 September 2015;revised 16 December 2015;accepted 17 December 2015 Available online 8 January 2016
Peer review under responsibility of China Ordnance Society.
*Corresponding author.Tel.:+8613605171926.
E-mail address:windieed@126.com (B.XU).
http://dx.doi.org/10.1016/j.dt.2015.12.005
2214-9147/© 2016 China Ordnance Society.Production and hosting by Elsevier B.V.All rights reserved.
© 2016 China Ordnance Society.Production and hosting by Elsevier B.V.All rights reserved.
- Defence Technology的其它文章
- The ballistic performance of the bombard Mons Meg
- Innovative boron nitride-doped propellants
- Application of transient burning rate model of solid propellant in electrothermal-chemical launch simulation
- 3D numerical simulation and analysis of railgun gouging mechanism
- Mechanism of plasma ignition in electrothermal-chemical launcher

