基于最大裂缝宽度的钢筋混凝土楼板可靠度分析

王立宪，杨万辉，狄生奎，项长生

(兰州理工大学甘肃省土木工程防灾减灾重点实验室，兰州 730050)

基于最大裂缝宽度的钢筋混凝土楼板可靠度分析

王立宪，杨万辉，狄生奎，项长生

(兰州理工大学甘肃省土木工程防灾减灾重点实验室，兰州 730050)

根据一次二阶矩中的验算点法可靠度理论，基于最大裂缝宽度指标中钢筋混凝土构件极限状态下的功能函数，分析了各随机变量的分布类型，利用MATLAB编程实现可靠指标验算。通过计算实例分析了各随机变量对最大裂缝宽度可靠指标灵敏性的影响，数值结果表明:混凝土保护层厚度、楼板有效高度、混凝土轴心抗拉强度以及荷载效应比对可靠指标及灵敏度有不同的影响，本文结论可为钢筋混凝土板式构件的设计提供相关理论依据与指导。

可靠度;灵敏度;最大裂缝宽度;钢筋混凝土楼板

近年来，板式结构坍塌事故频繁出现，造成了巨大的人员伤亡和经济损失。重大土木工程结构的安全失效问题逐渐引起人们的广泛关注，对结构的安全状态评估进而成为专家学者研究的热门领域。史志华等［1］基于一次二阶矩法，对钢筋混凝土构件在正常使用极限状态下的可靠指标进行验算，达到了预期的效果;Val D V等［2］提出了锈蚀钢筋混凝土板式桥梁的可靠度评估方法，建立了荷载模型、钢筋锈蚀模型和非线性有限元结构模型，根据一次二阶矩法对可靠度指标进行估计;蒋伟等［3］分析了钢管混凝土拱面外稳定的可靠度与灵敏度，发现混凝土强度的灵敏度随外荷载的增大而增大，随弹性模量的增大而减小;焦美菊等［4］基于最大裂缝宽度，对钢筋混凝土桥梁进行了可靠度分析，结果表明可靠指标基本满足设计要求。目前，国内外对于板式构件在正常使用极限状态下的安全评估研究较少，但以概率度量为理论基础的结构可靠度相关理论发展较为成熟，充分考虑了影响结构的诸多不确定性因素。因此，本文以板式结构构件的最大裂缝宽度指标作为考察结构可靠度评估对象，首先根据规范对板式受弯构件进行最大裂缝宽度分析，再确定各变量的分布类型，最后利用基于验算点法的可靠度计算方法结合具体的实例对钢筋混凝土楼板进行了最大裂缝宽度可靠指标计算，并对其灵敏性进行了分析。

1 最大裂缝可靠度分析

1.1 结构可靠度

根据《建筑结构可靠度设计统一标准》(GB 50068—2001)［5］规定，结构可靠性的定义为:在规定的时间内、规定的条件下，结构完成预定功能的概率，它包括三方面的内容，即安全性、适用性、耐久性。结构的安全性一般基于承载力极限状态设计，而适用性与耐久性则是基于正常使用极限状态设计考虑。

当结构的极限状态方程由若干变量综合而成的荷载作用效应以及结构对外荷载的抗力两方面表示时，结构的极限状态方程可表达为

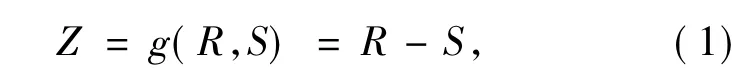
式中:R为结构或构件的抗力，S为荷载作用效应。

我国现行标准《混凝土结构设计规范》(GB 50010—2010)［6］对裂缝宽度有一定要求，当构件裂缝宽度过大时，会严重影响建筑的适用性。由此，可对正常使用极限状态控制设计的混凝土结构构件进行可靠度分析。

在正常使用状态下由裂缝宽度控制的混凝土受弯构件中的最大裂缝宽度按下式计算

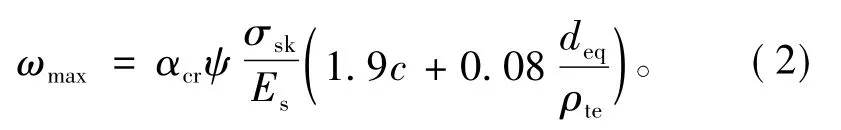
式中:αcr为构件受力特征系数，对于受弯和偏心受压的混凝土构件取1.9;ψ为受拉钢筋应变不均匀系数;σsk为按荷载标准组合计算的钢筋混凝土构件纵向受拉钢筋应力;Es为钢筋弹性模量;c为混凝土保护层厚度;ρte为纵向受拉钢筋的配筋率;Ate为有效受拉混凝土截面面积;As为受拉区纵向钢筋截面面积;deq为受拉区纵向钢筋的等效直径。

对于正常使用极限状态，将规范规定的裂缝宽度限值作为结构构件对外荷载的抗力。依据《混凝土结构设计规范》(GB 50010—2010)规定，在Ⅰ类和Ⅱ类环境下，钢筋混凝土构件的最大裂缝宽度不得超过0.3 mm。

1.2 极限状态方程

在最大裂缝宽度的可靠度分析中，认为构件的抗力为0.2 mm，而作用的效应为混凝土构件在实际荷载作用下产生的最大裂缝宽度。采用《混凝土结构设计规范》(GB 50010—2010)中规定的计算公式得到的计算值，并引入计算模式不确定系数γ加以修正，则可建立基于最大裂缝宽度的钢筋混凝土构件正常使用极限状态方程［7－8］

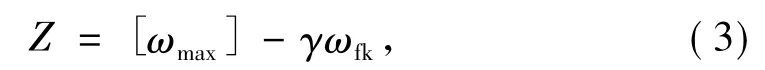
式中:γ为构件裂缝宽度计算模式不确定系数。综合以上各式，可得极限状态方程为

2 基于验算点法的可靠指标计算

目前，可靠度理论发展已较为成熟。常用的可靠度计算方法有蒙特卡洛(Monte Carlo)方法、响应面法、随机有限元法、一次二阶矩法、二次二阶矩法及高次高阶矩方法。根据《建筑结构可靠度设计统一标准》(GB 50068—2001)，钢筋混凝土楼板所受恒荷载及其几何参数基本服从正态分布，其所受各类活荷载则服从极值Ⅰ型分布。根据已有结构荷载的分布类型及其已知条件综合考虑，宜采用一次二阶矩当中的验算点法作为可靠指标的计算方法［9－10］。

在使用基于一次二阶矩中的验算点法进行结构可靠度计算时，可靠指标β的几何意义为:在标准正态坐标系中，坐标原点到极限状态曲面的距离，垂足即为验算点。将非线性功能函数在验算点处展开，并取一次项［4］

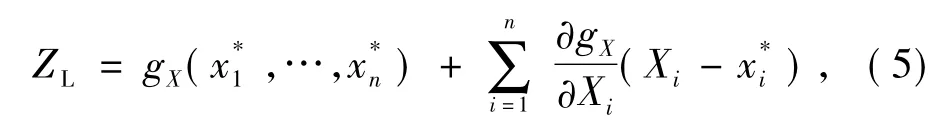
则其平均值与方差分别为

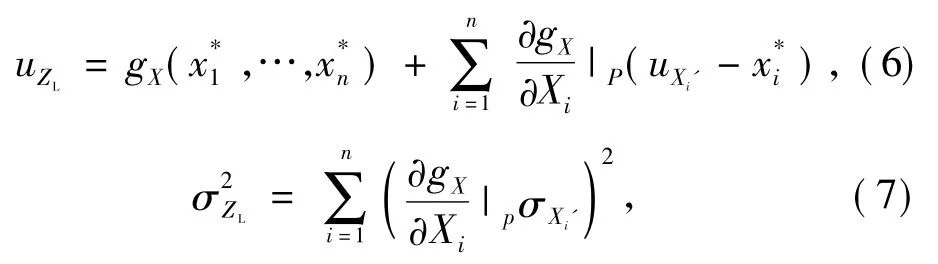
则可靠指标为

由式(8)可知，可靠指标β为验算点的坐标值函数，因为此验算点的坐标值未知，所以需要补充其他条件。而验算点与可靠指标有以下关系:

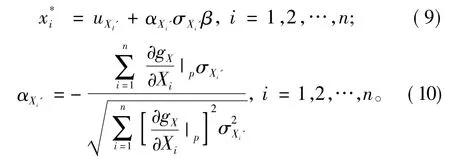
其中，αXi'为随机变量灵敏度系数。可靠指标β由式(5)～(10)组成的非线性方程组迭代计算可得，其迭代步骤具体为:①选定初始验算点，一般取x*(0)= (ux1，ux2，…，uxn);②由式(6)、(7)计算均值uX和方差σX;③由式(8)计算可靠指标β;④由式(10)计算αXi'(i =1，2，…，n);⑤由式(10)计算新的验算点为规定的允许误差，则停止迭代，所求β即为要求的可靠指标;否则，取x*(1)=x*(0)，转第②步继续迭代。

3 算例及可靠指标分析

3.1 算例1

某现浇简支单向板，板厚为150 mm，计算跨度为2.7 m，承受恒荷载标准值gk=0.8 kN/m2(不包括板自重)，活荷载标准值qk=2.5 kN/m2，采用混凝土强度等级为C30，HPB300级钢筋。钢筋混凝土自重为25 kN/m3，不考虑受压钢筋作用。

3.2 算例2

具体参数同算例1，楼板结构形式为双向板，采用双向板计算方法，考查基于裂缝宽度的各随机变量可靠度。根据文献 ［10］查得各随机变量的统计参数见表1。

表1 各随机变量统计参数表Table 1 Statistical parameters of random variables

用MATLAB软件基于一次二阶矩法编程进行可靠指标计算，经过多次迭代最终满足精度要求，得到不同变量变化时与可靠指标β的关系图。图1～图4分别表示在不同混凝土保护层厚度c、楼板有效高度h、混凝土抗拉强度ftk以及不同荷载效应比下的钢筋混凝土双向板与单向板可靠指标β之间的关系曲线。

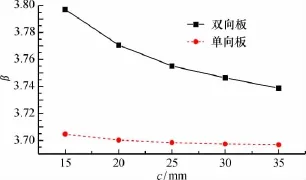
图1 混凝土保护层厚度c与可靠指标β关系Fig.1 Relationship between thickness c of concrete protection and reliability indexβ

图2 楼板有效高度h与可靠指标β关系Fig.2 Relationship between effective height h of floors and reliability indexβ

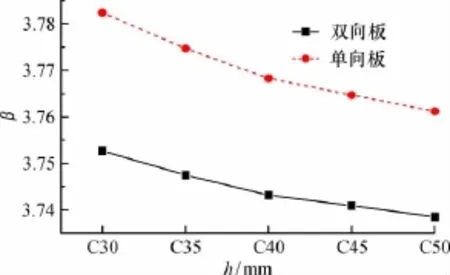
图3 混凝土抗拉强度ftk与可靠指标β关系Fig.3 Relationship between tensile strength ftkof concrete and reliability indexβ

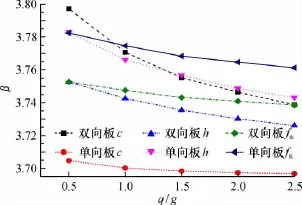
图4 荷载效应比q/g与可靠指标β关系Fig.4 Relationship between load effect ratio q/g and reliability indexβ

由图1可知，其他变量一定时，相同保护层厚度的双向板可靠指标高出单向板可靠指标约5%。由图2和图3可知，相同楼板有效厚度h和混凝土抗拉强度ftk的单向板可靠指标高出双向板可靠指标约3%。从图4中可以看出，其他变量一定时，随着荷载效应比q/g的增大，双向板保护层厚度的增大使可靠指标下降的程度较其他随机变量更为明显，其可靠指标高出同等条件下单向板的5%～10%。同等楼板有效高度h和混凝土强度ftk情况下，单向板可靠指标高出双向板约4%。

3.3 可靠指标灵敏性分析

可靠度对于随机参数灵敏性分析是结构可靠性研究的一个重要方面，为了分析不同随机变量参数对可靠指标的影响程度，通过改变楼板的保护层厚度c、有效高度h、混凝土抗拉强度ftk等参数，得到了计算模式不确定性系数γ、恒荷载作用g、活荷载作用q对可靠指标的灵敏度系数α，具体结果见表2。

由计算结果可知，在不同的保护层厚度c、楼板有效高度h以及混凝土抗拉强度ftk下，双向板与单向板的计算模式不确定性系数γ、恒荷载效应g、活荷载效应q的灵敏度基本保持一致，没有明显差异。不确定性系数γ的灵敏性基本保持在0.984 1～0.999 8，恒荷载作用 g基本保持在0.004 3～0.038 4，活荷载作用 q基本保持在0.019 5～0.173 5。不确定性系数γ的灵敏性远远高于恒荷载作用g与活荷载作用q。由此可知，不确定性系数对可靠指标的灵敏性最大，在计算过程中应予以考虑。

表2 随机变量灵敏度参数Table 2 Random variable parameter sensitivity

图5 荷载效应比q/g与灵敏度数α关系Fig.5 Relationship between load effect ratio q/g andα

图5表明在不同的荷载比q/g下，保护层厚度c、楼板有效高度h以及混凝土抗拉强度ftk的灵敏程度有所不同。计算结果表明，随着荷载效应比的增大，双向板与单向板的保护层厚度的灵敏性逐渐降低:荷载比q/g在0.5～1.5，保护等厚度c的灵敏度表现平缓;在1.5～2.0时，双向板c的灵敏度急剧下降。恒荷载效应约为2倍的活荷载效应时，保护层厚度对双向板与单向板的灵敏度出现跳跃，表现出较为明显的差异;楼板有效高度h、混凝土抗拉强度ftk对双向板与单向板的灵敏度在q/g为1.5～2.5范围时无明显差异，基本一致。

4 结论

通过对最大裂缝控制的钢筋混凝土楼板在正常使用极限状态下的可靠度与灵敏度分析，得出以下结论:

(1)从影响钢筋混凝土楼板可靠度的众多因素中发现，在其他变量一定的情况下，同等保护层厚度的双向板可靠指标高出单向板可靠指标约5%，同等楼板有效厚度h和混凝土抗拉强度ftk的单向板可靠指标高出双向板可靠指标约3%。

(2)在不同的保护层厚度c、楼板有效高度h以及混凝土抗拉强度ftk下，双向板与单向板的计算模式不确定性系数γ、恒荷载效应g、活荷载效应q的灵敏度基本保持一致，没有明显差异。

(3)恒荷载效应约为2倍的活荷载效应时，保护层厚度对双向板与单向板的灵敏度有明显差异，而楼板有效高度h、混凝土抗拉强度ftk对双向板与单向板的灵敏度在q/g为1.5～2.5时无明显差异，基本一致。

［1］史志华，胡德炘，陈基发，等．钢筋混凝土结构构件正常使用极限状态可靠度的研究［J］．建筑科学，2000，16 (6):4－11．

［2］Val D V，Stewart M G，Melchers R E．Effect of reinforcement corrosion on reliability of highway bridges［J］．Engineering Structures，1998，20(11):1010－1019．

［3］蒋伟，吕大刚．钢管混凝土拱面稳定的可靠度与灵敏度分析［J］．哈尔滨工业大学学报，2012，44(12):8－12．

［4］焦美菊，孙利民．基于最大裂缝宽度的钢筋混凝土桥梁可靠度分析［J］．工程力学，2010，27(S1):245－249．

［5］GB 50068—2001，建筑结构可靠度设计统一标准［S］．

［6］GB 50010—2010，混凝土结构设计规范［S］．

［7］赵羽习，金伟良．正常使用极限状态下的混凝土结构构件可靠度的分析方法［J］．浙江大学学报:工学版，2002，36(6):674－679．

［8］杨伟军，赵传智．土木工程结构可靠度理论与设计［M］．北京:人民交通出版社，1999:73－78．

［9］Gayton N，Bourient JM，Lemaire M.CQ2RS:A new statistical approach to the response surfacemethod for reliability analysis［J］．Structural Safety，2003，25(1):99－121．

［10］贡金鑫，魏巍巍．工程结构可靠性设计原理［M］．北京:机械工业出版社，2007．

Reliability analysis of reinforced concrete slabs based on themaximum crack w idth

WANG Li-xian，YANGWan-hui，DISheng-kui，XIANG Chang-sheng
(Key Laboratory of Disaster Prevention and Mitigation in Civil Engineering of Gansu Province，Lanzhou University of Technology，Lanzhou 730050，China)

In this paper，the distribution of each random variable in reinforced concrete members under the maximum crack width index is analyzed based on specification of function limit state．According to the checking pointmethod of the reliability theory，reliability index is calculated by MATLAB program．The random variable of the reliability index is studied to discuss the sensitivity of themaximum crack width index，through specific examples．The results show that the thickness of concrete cover，floor height，concrete axial tensile strength and load effect on the reliability index have different effects on reliability index and sensitivity．The result can provide theoretical basis and suggestion for the design of reinforced concrete slabs．

reliability;sensitivity;themaximum crack width;reinforced concrete floor

TU375.2;TU311.2

:A

2015－07－07

国家自然科学基金项目 (51608245);甘肃省科技计划项目 (148RJZA012)

王立宪 (1977—)，男，博士研究生，讲师，研究方向:结构健康监测，wanglxian@lut.cn。

王立宪，杨万辉，狄生奎，等．基于最大裂缝宽度的钢筋混凝土楼板可靠度分析［J］．桂林理工大学学报，2016，36(4):721－725．

1674－9057(2016)04－0721－05

10.3969/j．issn.1674－9057.2016.04.012