遗传算法优化刀具角度对加工变形控制的研究*

于　金，高彦梁

(沈阳航空航天大学 机电工程学院，沈阳　110136)



遗传算法优化刀具角度对加工变形控制的研究*

于金，高彦梁

(沈阳航空航天大学 机电工程学院，沈阳110136)

摘要：针对航空钛合金薄壁件的铣削变形问题，采用钛合金专用铣刀对该零件进行模拟加工(ABAQUS软件)和实际加工，验证了有限元分析模型的有效性的同时得出关键路径的平均变形量；借助遗传算法以铣削力预测模型为目标函数，对铣刀几何角度进行优化，得到理论最优刀具几何角度γ=6°、α=16°、β=44°,采用最优几何角度的铣刀模拟加工工件获得的平均变形量更小。结果表明，遗传算法在优化铣刀角度方面是一种有效的方法，依据此方法能够制定出较为合理的刀具几何角度组合以控制薄壁件的加工变形。

关键词：薄壁件；有限元；遗传算法；刀具角度；加工变形

0引言

钛合金材质的薄壁零件在铣削加工中极易发生变形，影响被加工对象的最终加工质量及精度。应用有限元分析技术研究和解决航空薄壁件加工变形问题已成为当前研究的热点和重要手段之一。目前许多学者利用有限元分析方法对薄壁件的加工变形进行了大量的研究。S. Ratchev[1]等在建立了柔性力学模型的基础上成功实现了对低刚度薄壁件加工变形预测的有限元模拟分析；高翔[2]等人采用遗传算法对薄壁件夹具布局和加紧力进行同步优化，使得因装夹不当引起的加工变形降低，提高了加工精度。这些研究仅限于在典型零件及在未知工况的情况下进行研究分析，没有具体的针对实际零件进行具体分析。

胡权威，乔丽红[3]等人针对薄壁件刚性差、易产生加工变形等问题，提出一种有限元正交优势分析方法,用以优化铣削参数,减小铣削产生的零件变形；郭魂、左敦稳[4]等人对在铣削力和初始残余应力场作用下的薄壁件分析计算，研究加工参数对加工变形的影响规律。这些研究仅考虑了铣削工艺参数的影响，忽略了铣削刀具的几何参数。

本文主要针对航空发动机内部的薄壁件进行研究。采用钛合金专用铣刀建立了加工变形的有限元模型，并设计验证性试验证明有限元分析模型的有效性。借助遗传算法的全局寻优能力，以铣削力预测模型为目标函数，对铣刀几何角度进行优化分析，得到理论最优刀具几何角度，与专用铣刀获得的最优结果比较分析，得出遗传算法在优选刀具角度方面的优越性。该方法为合理的选用铣刀以控制薄壁件加工变形提供了有效途径，且能够应用在其他机切加工刀具的设计上。

1薄壁件加工变形有限元仿真关键技术

1.1建立三维铣削有限元模型

零件和刀具装配情况如图1所示,Path-X和Path-Y为测量薄壁件加工变形的关键测量线。零件属于某型号飞机发动机薄壁件，工件材料为钛合金TC4，航空薄壁件的内腔由两个薄壁、底部及后部结构组成，两侧薄壁厚度2mm。验证性实验加工过程中采用钛合金专用铣刀前角γ=10°、后角α=15°、螺旋角β=40°的四齿直柄立铣刀，刀具直径d=10mm，材料为硬质合金YG8[5]。

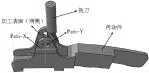
图1　铣刀与零件装配示意图

1.2材料本构模型

在金属切削领域用于描述材料本构关系的理论模型为Johnson-Cook模型。该模型的表达式如式(1)所示[6]。

(1)

表1　TC4材料的Johnson-Cook模型参数

1.3铣削加工中切屑的形成准则

目前很多研究表明钛合金加工过程中材料的破坏遵循Johnson-Cook动态失效模型，当破坏值大于1时，断裂破坏随之发生[8]。材料破坏的相关参数满足关系式(2)。

(2)

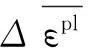
(3)

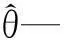
表2　TC4的Johnson-Cook剪切失效模型参数

2实验验证

为了验证有限元分析结果的正确性及合理性，本文采用钛合金专用铣刀对薄壁件进行实际切削和模拟加工。实验所采用的机床为XKA714C数控铣床，铣削模拟过程的等效塑性应力分布云图和加工现场如图2和图3所示。切削结束零件应力稳定后用三坐标测量仪对零件关键路径上点的变形进行选点测量。将试验所测得的X路径和Y路径上各点的变形量数据与模拟值进行比较，得到曲线图如图4a和图4b所示，无论是模拟值的变形大小和变形趋势与实验值都有较好的吻合度从而验证了模拟结果的正确性，模拟切削得到Path-X路径平均变形量为δx1=0.0216mm，Path-Y路径平均变形量为δy1=0.0115mm。

图2　等效塑性应力分布云图

图3　加工现场

图4　Path-X和Path-Y路径仿真值与实验值比较

3遗传算法对刀具角度的优化

遗传算法模拟了自然进化的过程，通过分辨染色体结构中的特征基因来确定适应能力强的染色体，以此来达到设定的目标[9]。

3.1优化目标的建立

本文研究的问题是薄壁件铣削加工铣刀角度优化的问题，所以问题的参数集问题为：薄壁件铣削加工变形量最小时，所选取的铣刀前角γ、后角α和螺旋角β的组合。由于薄壁件产生加工变形的主要因素是切削力，因此优化铣刀角度的过程中要以控制加工过程中工件的铣削力最小为目标函数以控制零件的变形。

已知刀具前角的影响系数计算公式为：

(4)

式中：C——常数[10-11]。

由于除了角度以外的其他参数都是相同的，故设为常数，则切削力关于前角、后角和螺旋角的公式为：

(5)

式中：C1、C2、C3、C4、C5—常数[12]。

上式可化简为：

F=k1(k2-γ)k3αk4βk5

(6)

式中：k1、k2、k3、k4、k5—常数。

两边同时取对数得：

lnF=lnk1+k3ln(k2-γ)+k4lnα+k5lnβ=

(7)

由泰勒公式得：

(n=1,2,3,…)

(8)

(9)

(10)

设y=lnF，x1=lnk1，x2=lnk2，x3=k3，x4=k4，x5=k5

则由(7)式得：

(11)

式(11)为评价群体优劣的目标函数。

3.2约束条件

根据铣削力、刀具角度和机床功率的要求，优化目标的主要约束条件有[13]：

铣削力约束：

(12)

式中：F—主切削力；Fmax—最大主切削力；C—系数，取决于被加工材料和切削条件；m、n、p—ap、f、v的指数；K—切削力修正系数。

刀具角度约束：

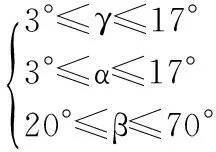
(13)

机床功率约束：

(14)

式中：η—机床效率；Pmax—机床最大功率。

3.3遗传算法求解

在MATLAB中通过应用GATOOL遗传算法工具箱设置个体的数量为N=80，最大遗传代数为M=100，交叉概率Pc=0.4，变异概率Pm=0.08。编写MATLAB代码，运行程序，经过71次迭代最终获得在最小切削力下所对应的变量值即刀具角度。各铣刀角度过程的收敛情况如图5所示，其中横坐标是进化代数，纵坐标为目标函数值(适值)，即关键面上路径Path-X的所有个体切削力的值。可由图看出，随着遗传算法优化的不断进行，工件材料铣削力不断降低。最终在进化代数到71代时迭代终止，获得铣刀各角度的最优结果为：前角γ=6°、后角α=16°、螺旋角β=44°。以此铣刀角度进行模拟铣削加工，得到的平均变形值为δx2=0.0141mm<δx1，δy2=0.0092mm<δy1，优于钛合金专用铣刀所得的结果。

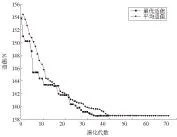
图5　遗传算法迭代结果

4结论

(1)本文针对典型的航空发动机薄壁件的加工变形进行分析，运用有限元和实际加工相结合的方法，验证了有限元模型的有效性。其中，分离准则和本构模型等有限元关键技术的正确选取都对模型的准确性具有重要意义。

(2)借助 MATLAB 遗传算法工具箱，编写相应的遗传算法程序，以刀具前角、后角、螺旋角作为设计变量，切削力最小为目标函数。建立薄壁件铣削加工铣刀角度优化模型，遗传算法优化所得铣刀各角度的最优结果为前角γ=6°、后角α=16°、螺旋角β=44°。铣削加工获得的变形量为δx2=0.0141mm，δy2=0.0092mm，优于专用钛合金铣刀所得结果。证明这是合理的改善最优几何角度组合以控制薄壁件加工变形的方法。

[参考文献]

[1] Ratchev S,Liu S,Huang W,et al. A flexible force model for the end milling of low-rigidity parts[J]. Journal of Materials Processing Technology,2004, 153-154: 134-138.

[2] 高翔，张连文，王勇.薄壁零件装夹方案设计与优化[J].组合机床与自动化加工技术,2009(6):9-12.

[3] 胡权威,乔丽红,张洪伟.薄壁结构件铣削参数有限元正交优势分析及优化[J].机械工程学报，2013,49(21):176-184.

[4] 郭魂，左敦稳，刘远伟,等.航空腔型薄壁件铣削变形的预测[J].吉林大学学报(工学版),2008,38(1):84-88.

[5] 邵军杰.钛合金专用铣刀参数化设计及其试验研究[D].上海:上海交通大学，2009.

[6] Johnson G R,Cook W H.A constitutive model and data for metals subjected to large strains ,high strain rates and high temperature[C].Proceedings of the 7th International Symposium on Ballistics.Netherlands:1983:541-547.

[7] Akbari Mousavi S A A,Shahab A R,Mastoori M.Computational study of Ti-6Al-4V flow behaviors during the twist extrusion process[J]. Materials and Design,2007,29 :1316-1329.

[8] 丁子昀, 左敦稳, 郭魂,等. 多点装夹方案对多框体铣削变形影响的有限元分析[J].南京航空航天大学学报,2009,41(5):639-643.

[9] 吴玲，左健民，王保升,等.基于遗传算法的铣削参数优化[J].组合机床与自动化加工技术，2014(4):23-25.

[10] Saglam Haci,Unsacar Faruk,Yaldiz Suleyman.Investigation of the effect of rake angle and approaching angle on main cutting force and tool tip temperature[J].International Journal of Machine Tools & Manufacture , 2006, 46:132-141.

[11] Fromentin Guillaume，Poulachon Gerard. Geometrical analysis of thread milling-part1:Evaluation of tool angles[J].Int J Adv Manuf Technol, 2010,49:73-80.

[12] 潘永志,艾兴,唐志涛,等. 基于切削力预测模型的刀具几何参数和切削参数优化[J]. 中国机械工程，2008,19(4):428-431.

[13] 刘伟，王太勇.基于Pareto遗传算法的切削用量优化[J].农业机械学报，2011,42(2):220-234.

(编辑李秀敏)

Study on GA Optimize Tool Angels to Control Milling Deformation

YU Jin,GAO Yan-liang

(School of Mechatronic Engineering，Shenyang Aerospace University，Shenyang 110136，China)

Abstract：In view of the machining deformation of thin-walled parts,the paper adopts the special milling cutter for titanium alloy to carry on simulating machining(ABAQUS software) and actual machining,by comparing with the results,the validity of the finite element method is verified and gets the average deformation of the critical path;Genetic algorithm was introduced for optimization analysis because of its excellent global optimization ability,and regarded the milling force prediction model as the objective function, the optimal combination is γ=6°,α=16°,β=44°.After experimental verification:the optimal milling cutter angels obtained by genetic algorithm can make the average deformation less in the process of machining.The results show that genetic algorithm is an efficient method suitable for optimum tool angels.

Key words：thin-walled parts；finite element analysis；genetic algorithm；milling cutter angle；machining deformation

中图分类号：TH164；TG54

文献标识码：A

作者简介：于金(1961—)，男，辽宁大连人，沈阳航空航天大学教授，硕士，研究方向为数控加工、机电一体化技术，(E-mail)yujin@sau.edu.cn。

*基金项目：辽宁省自然科学基金(2014024006)

收稿日期：2015-05-05

文章编号：1001-2265(2016)03-0141-03

DOI:10.13462/j.cnki.mmtamt.2016.03.039