基于自适应进化相关向量机的城市需水量预测模型研究

徐继红

(新疆塔里木河流域管理局， 新疆 库尔勒　841000)



基于自适应进化相关向量机的城市需水量预测模型研究

徐继红

(新疆塔里木河流域管理局， 新疆 库尔勒841000)

【摘要】为改进城市需水量预测模型，将相关向量机与差分进化优化算法进行融合及改进，提出基于自适应进化相关向量机的需水量预测模型。以新疆阿克苏市为例，建立基于自适应进化相关向量机的城市需水量预测模型，并与多元线性回归、BP神经网络、支持向量机算法在精度与可靠性方面进行对比分析。结果表明:新模型预测精度大约是上述其他方法的2倍以上； 测试数据的实际需水量均在自适应进化相关向量机估计的95%置信度的置信区间内，并且由后验差比、小误差概率判定模型等级属于“好”级别。

【关键词】城市需水量； 预测； 自适应进化； 相关向量机

随着城市对水资源需求的日益提高，对城市需水量进行科学的分析和预测是满足城市发展需求、保证水资源可持续利用的前提。因此，如何构建城市需水量与其驱动力之间复杂的函数模型、预测需水量变化成为当今水资源规划利用的热点问题。当前，传统需水量预测模型主要包括线性回归模型、时间序列分析、灰色理论等[1-2]。但这些模型未充分综合考虑社会、自然与经济等复杂影响因素对需水量变化的影响，导致拟合精度不高。随着神经网络及元胞自动机等人工智能算法的提出，人工智能、机器学习(如SVM)等方法的应用，预测精度较传统方法有较大提高。但这些方法重点集中在预测精度提高方面，对算法稀疏化及预测结果的不确定性分析很少，研究稀疏化和具有概率意义的城市需水量预测模型对提高模型精度及结果可靠性具有重要意义。

相关向量机[3- 4]是一种贝叶斯框架下的稀疏概率模型，该算法在具有稀疏性的同时可获得预测结果的不确定性信息，且算法待定参数少，核函数不受Mercer条件限制。这在解决诸多模式识别和回归估计的实际问题中取得了良好效果，但在城市需水量预测方面未见相关研究。因此，本文将该算法应用于需水量预测，并将全局搜索能力强、鲁棒性好与收敛速度快的自适应差分进化算法[5]与相关向量机结合，优化相关向量机待定参数，提出基于自适应进化相关向量机的城市需水量预测模型。以新疆阿克苏市需水量预测为例，分析基于自适应进化相关向量机的预测模型建立过程，并与多种需水量预测方法进行对比分析，证明本文方法在模型精度、可靠性及稀疏性方面的优点，以期为相关向量机进一步研究应用提供参考。

1自适应进化相关向量机模型

本文利用自适应差分进化算法自适应确定相关向量机待定参数，提出自适应进化相关向量机模型(self-adaptive differential evolution-relevance vector machine，SADE-RVM)，以提高模型预测精度。

1.1自适应差分进化算法构建

差分进化算法(differential evolution，DE)是一种基于实数编码的群体智能理论的优化算法，算法原理类似于遗传算法[6]。通过群体内个体间的合作与竞争产生的群体智能指导优化搜索，因此该算法有更好的全局搜索能力、鲁棒性与收敛速度。该算法通过对种群中的个体进行变异、交叉、选择操作，获得最优个体，确定最优值。鉴于算法的缩比因子F和交叉概率Cr参数对算法影响较大，本文构建F与Cr参数自适应的DE算法(self-adaptive differential evolution，SADE)[7]，算法工作原理如下：

a.变异操作。对n代m个体vm(n)进行变异操作，在种群数量范围内随机选取不同r1、r2、r3号vr1(n)、vr2(n)、vr3(n)按照式(1)进行变异操作，产生n+1代个体vm(n+1)。

(1)

b.交叉操作。对个体vm(n)与个体vm(n+1)的d的维数按照式(2)进行交叉，产生个体um(n+1)。Cr为交叉概率，k为在1与最大维数之间随机产生的整数，保证至少有一维数进行交叉。

(2)

c.选择操作。以适应度大小为个体优劣判定依据，对个体vm(n)与um(n+1)进行选择，优选个体加入下一代种群。

针对F、Cr参数对算法性能影响较大这一问题，依据当前个体适应与最大、最小适应度之间关系采取策略式(3)、式(4)对参数进行自适应调整，提高算法可靠性。

(3)

(4)

式中Fmax、Fmin——最大、最小缩比因子；

Crmax、Crmin——最大、最小交叉概率；

fmax(n)、fmin(n)——n代最大、最小适应度；

fm——m个体适应度。

1.2模型构建

根据SADE与RVM算法特点，以留一交叉验证法建立SADE算法的适应度函数[8]，自适应确定RVM模型最优参数，提出SADE-RVM模型，减少人为参数确定不当对RVM算法性能的不利影响。

1.3模型精度评价方法

为对模型精度进行合理评价，选取3种预测模型进行对比分析。建立定量与定性的模型精度评价指标，对自适应进化向量机模型精度做出科学、合理的评价。

a.对比模型的建立。选取多元线性回归、BP神经网络、最小二乘支持向量机作为对比模型，分别建立预测模型，以Matlab编程实现，具体建模过程如下：ⓐ多元线性回归模型(multivariate linear regression，MLR)：以影响需水量变化的7种因素为模型输入、城市需水量为模型输出，以regress函数求解模型参数，建立多元线性回归预测模型；ⓑBP神经网络：以影响需水量变化的7种因素为模型输入、需水量为模型输出，1个隐含层、6个神经元，传递函数包括{‘logsig’，‘tansig’}，以trainlm函数为训练函数，建立基于BP神经网络的预测模型；ⓒ最小二乘支持向量机(least squares support vector machine，LS-SVM)：以影响需水量变化的7种因素为模型输入、需水量为模型输出，选择径向基核函数作为算法核函数，以网格搜索法通过多次试算，确定最小二乘支持向量机的2个参数，建立预测模型。

b.模型精度评价方法。选取平均绝对误差(mean absolute error，MAE)、平均相对误差(mean relative error， MRE)、均方根误差(root mean square error，RMSE)3个精度指标评价各模型精度优劣。

根据后验差比C及小误差概率P[9]对需水量变化预测模型精度进行等级划分，对各预测模型进行定性评价，具体见表1。

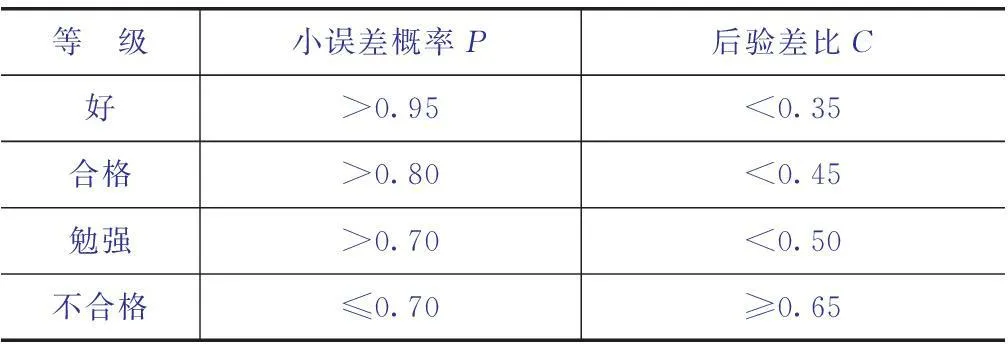
表1　城市需水量预测模型精度等级划分

2模型应用

本文以新疆阿克苏市城市需水量变化为例，建立自适应进化预测模型。

2.1建模数据源

城市需水量变化受社会、自然、经济等方面的多种因素影响，通过参考《阿克苏市统计年鉴》[10-11]，收集该市1990—2005年城市需水量(y)及其影响因素数据(见表2)。由于各变量单位不同，对建模精度有较大影响。因此，需对原始数据进行归一化处理后才可用于模型建立。表2中，x1为GDP(万元)，x2为人均GDP(元),x3为固定资产投资(万元)，x4为工业个数(个)，x5为城市人口(万人)，x6为供水总量(万m3)，x7为人均日生活用水量(L/d)，y为城市需水量(万m3)。

表2　阿克苏市1990—2005年需水量及其影响因子

2.2预测模型构建

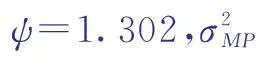
2.3结果评价

将测试数据集输入预测模型，预测2001—2005年需水量，同时建立95%置信度的置信区间[12]。为评价自适应进化相关向量机对需水量预测的精度，基于多元线性回归、BP算法、LS-SVM建立需水量预测模型。各模型预测结果见表3。

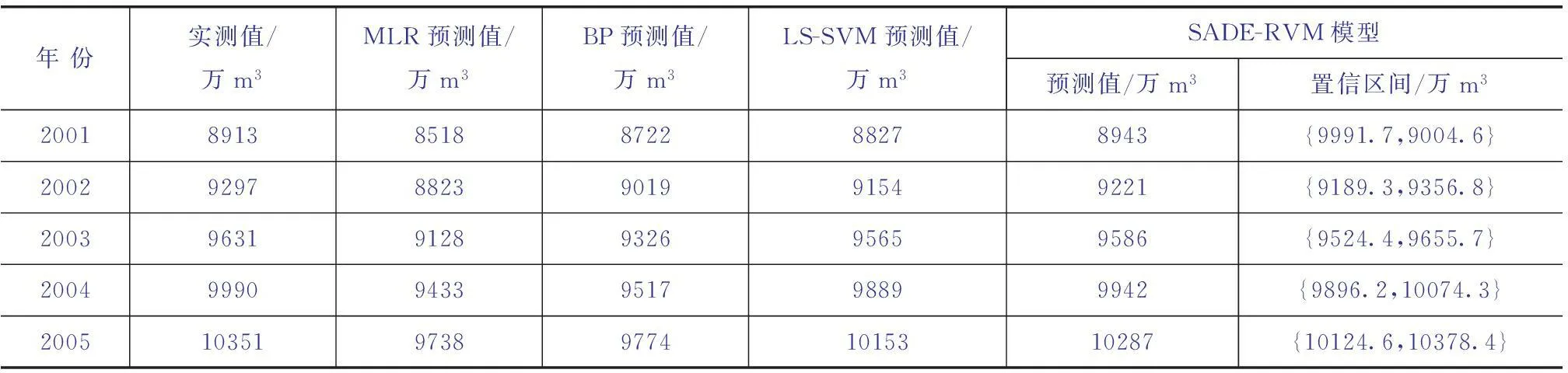
表3　需水量预测值和实测值

基于以上数据，计算各预测模型的MAE、MRE、RMSE、后验差比C、小误差概率P、模型等级等评价指标，具体结果见表4。

表4　预测模型评价指标

表3表明：2001—2005年需水量实际值均在自适应进化相关向量机估计的95%置信度区间内，证实预测结果可靠。由表4可知：自适应进化相关向量机各项精度指标表现最优，模型等级属于“好”，证实本文提出的新方法具有很高的预测精度。建立自适应进化相关向量机的城市需水量预测模型时，11组训练数据中只有3组为相关向量最终参与预测模型构建，有效简化了模型复杂度，具有很高的稀疏性。基于以上分析数据，自适应进化相关向量机的预测方法计算精度高、可靠性强。

3结论

a.本文提出的自适应进化相关向量机模型有效地解决了核函数参数确定问题，自适应优化核函数参数，可降低由于参数不当对模型精度的影响。

b.由MAE、MRE、RMSE数据可知：对于城市需水量预测，自适应进化相关向量机的精度大约是LS-SVM方法的2倍、BP网络的7倍、多元线

性回归的10倍。因此，自适应进化相关向量机对城市需水量预测有很高精度。

c.城市需水量实际值均在自适应进化相关向量机估计的置信区间内，定量地证实模型具有很强的可靠性。通过后验差比、小误差概率分析，自适应进化相关向量机对需水量预测结果等级属于“好”，定性地证实该模型具有很好的预测效果。

参考文献

[1]宓永宁,陈默,张茹.灰色拓扑法在大伙房水库总氮预测中的应用[J].水利建设与管理,2009(3):72-73.

[2]江智健.清华水电站直供电片区电力需求预测及其启示[J].中国水能及电气化,2013(10):45- 49.

[3]Tipping M E.Sparse bayesian learning and the relevance vector machine[J]. Journal of Machine Learning Research 2001,1(3):211-244.

[4]Bishop C M,Tipping M E.Variational relevance vector machine[C]//The 16th Conf on Uncertainty in Artificial Intelligence.USA:Morgan Kaufmann,2000.

[5]Storn R,Price K.Differential evolution:A simple and efficient beuristic for global optimization over continuous spaces[J].Journal of Global Optimization,1997,11(4):341-359.

[6]Price K,Storn R,Lampinen J.Differential evolution:A practical approach to global optimization[M].Berlin Heidelberg:Springer,2005.

[7]孙昌跃,刘德顺,段凯.基于差分进化算法的钻头波阻辨识研究[J].煤炭学报,2012,37(2)：350-355.

[8]刘学艺,李平,郜传厚.极限学习机的快速留一交叉验证算法[J].上海交通大学学报,2011,45(8)：1140-1146.

[9]陈怀录,冯东海.土地利用规划耕地预测方法对比研究——以甘肃省临夏市为例[J].西北师范大学学报：自然科学版,2011,47(1)：99-104.

[10]阿克苏地区统计局.阿克苏统计年鉴[Z].1990-2002.

[11]阿克苏地区行署办公室,阿克苏地区统计局.阿克苏统计年鉴[Z].2003-2005.

[12]Wang F F,Zhang Y R.Relevance vector machine technique for the inverse scattering problem[J].Chinese Physics B,2012,21(5):19-24.

Research on urban water demand forecast model based on adaptive evolution relevance vector machine

XU Jihong

(XinjiangTarimRiverBasinAdministration,Korla841000,China)

Abstract：The relevance vector machine and differential evolution optimization algorithm are converged and improved in order to improve urban water demand forecast model. Water demand forecast model based on adaptive evolution relevance vector machine is proposed. Aksu in Xinjiang is adopted as an example. Urban water demand forecast model based on adaptive evolution relevance vector machine is established. It is comparatively analyzed with multiple linear regression, BP neural network and support vector machine algorithm in terms of accuracy and reliability. The results show that new model forecast accuracy is about more than 2 times compared with other above-mentioned methods. Actual water demand of test day is in the confidence level of 95% confidence estimated by adaptive evolution relevance vector machine. It is determined that the model level belongs to ‘good’ level through posteriori difference ratio and small error probability.

Key words：urban water demand; forecast; adaptive evolution; relevance vector machine

中图分类号：TV214

文献标志码：A

文章编号：1005- 4774(2016)01-0045-04

DOI:10.16616/j.cnki.10-1326/TV.2016.01.013