高铁场景下基于LOS径的多普勒频偏估计研究

宋腾辉 谈振辉

【摘要】 高速移动场景下，用户与基站之间的相对速度非常高，这会产生较大的多普勒频偏，引起OFDM系统子载波正交性。本文研究了Moose算法，并在此基础上结合高铁信道特征提出一种新的基于LOS径的多普勒频偏估计方法，仿真结果显示估计性能较原方法有明显的改善。

【关键词】 OFDM Moose 多普勒频偏估计 高铁 LOS

一、引言

近年来高速铁路的发展非常迅速，考虑到高铁通信的复杂性，国际铁路联盟明确将LTE-R应用到高铁通信中。LTE系统下行链路采用OFDM技术，高速移动场景下多普勒频移会使OFDM子载波间的正交性受到破坏，恶化接收端的误码性能。

本文研究高铁场景下的OFDM多普勒频偏估计技术，具有较高的实用价值。

二、Moose多普勒频偏估计算法

Moose算法由P.Moose[1]首度提出，它是一种基于最大似然估计进行频偏估计的算法。设经过IFFT之后的OFDM块可以表示为如下：

P.Moose在假定系统已经完成了精准的符号定时同步的情况下，连续发送两个完全相同的OFDM符号来进行估计。其符号结构如下所示：

如图1所示，在一个循环前缀CP后面跟着两个完全相同的符号序列，长度为N，记为A，这两个A序列就是算法中用来进行频偏估计的序列，而两个序列中间没有插入循环前缀。接收机接收到的2N点序列可以表示为：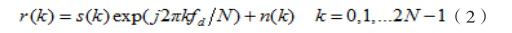

其中，fd为归一化多普勒频偏。

Y1n和Y2n表示受高斯噪声影响的接收信号，则多普勒频偏估计值如下所示：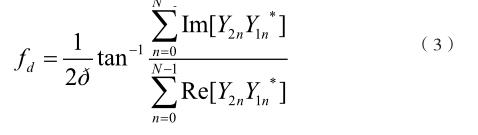

三、高铁多径时变信道建模

莱斯分布为视距路径分量很大且幅度已知，同时还存在大量独立路径，因此高铁信道模型在一般情况下属于莱斯衰落信道模型。因此高铁信道可以用莱斯信道建模，如下式所示[2]：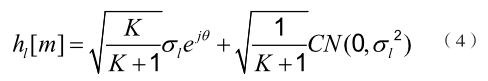

其中第一项表示以均匀相位θ到达的直射路径，第二项表示大量与θ相互独立的反射路径和散射路径总和。参数K为莱斯因子，是视距路径能量与散射路径能量之比，K越大，信道的确定性就越强，当K选取∞时，散射径足够小以至可以忽略，可以表示只有直射径的情况。

在本文高铁多径信道中，采用直射径与散射径分开加频偏的模型，其中直射径的频偏模型如式5所示：

从式5和6中可以看出多普勒频移在直射径中表现为直接频偏及产生时变信道，在散射径中则没有直接频偏的影响，仅体现在产生时变信道上。

四、基于LOS径的多普勒频偏估计算法

高铁场景下，信道中直射径较强，散射径较弱，接收信号以直射径传播的信号为主，因此可以考虑忽略散射径，直接使用直射径接收的信号做频偏估计。该方法不仅可以大大降低复杂度，而且在散射径较强的情况下，排除了散射径的干扰，也提高了系统的估计性能。

使用LOS径做接收的主要步骤如下图2所示：

首先使用接收信号做信道估计，求得信道响应。

其次从估计的信道响应中提取LOS径。将信道响应写为各径分离的形式：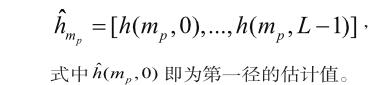

最后通过估计出的LOS径，求出LOS径上的接收信号，采用该信号做频偏估计。

在本文中假设已做完信道估计，即信道响应已知。信号经过信道后为LOS和散射径叠加的结果，在信道响应已知的情况下，采用总的接收信号减去散射径下接收到的信号作为LOS径接收的信号。

五、仿真实现

在本文的仿真中，多径信道选取一条强直射径与五条散射径。多径衰落系数为[0.0dB、-0.1dB、-9.0 dB、-10.0 dB、-15.0 dB、-20.0 dB]。

选取OFDM符号长度N=512，循环前缀长度L=32，子载波间隔Δf=15KHz，则采样频率为TS=1/（n*Δf）。多普勒频偏设置为fd=600Hz。

选取SNR从-10dB到15dB，K因子分别取6、8、10、20、∞。RUNS选取1000次以平滑曲线，降低随机性。Moose算法基于LOS径的仿真结果与原估计方法的比较如图3所示：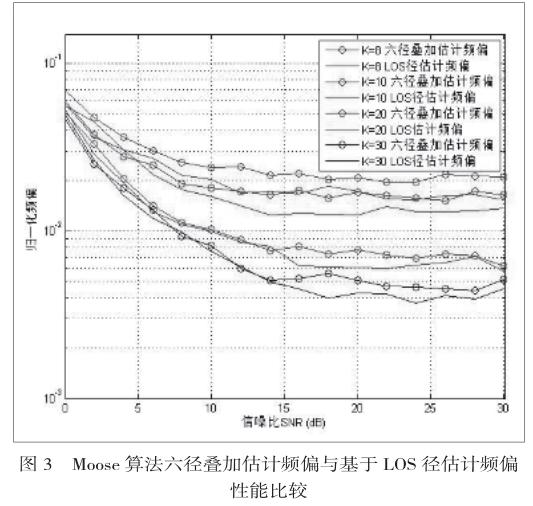

从图3可以看出，使用LOS径的估计误差要小于原方法的估计误差。在所取信噪比区间内，低信噪比下使用LOS径做频偏估计的性能与原方法估计频偏的性能在同K因子下两曲线相近，随着信噪比的增加，使用LOS做估计的性能要明显好于原方法的性能。而理论上，使用LOS径做估计减去了散射径的影响，性能应该好于六径叠加的情况，因此仿真结果与理论结果相符。而且在K因子较小的时候，LOS径的性能改善更明显，正是因为K因子较小时散射径相对较强，这时除去了较强的散射径只是用直射径做估计，性能改善更明显。

六、总结

结合高铁场景，本文研究了一种多普勒频偏估计算法-Moose算法，考虑到高铁信道一般具有较强的直射径，本文基于此提出了基于LOS径进行估计的方法，即忽略散射径只使用直射径接收的信号对频偏进行估计，仿真结果显示估计误差小于原方法，估计性能得到改善。

参 考 文 献

[1] Moose P H. A technique for orthogonal frequency division multiplexing frequency offset correction[J]. IEEE Transactions on Communications， 1994， 42（10）：2908-2914.

[2] David Tse，Pramod Viswanath. 李锵，周进.无线通信基础[M].北京：人民邮电出版社，2007：26-27.