孤网发电机调速系统参数定量调整理论分析

李 飞，肖仕武，王 琮，肖小清，郑李坤

孤网发电机调速系统参数定量调整理论分析

李 飞1，肖仕武1，王 琮1，肖小清2，郑李坤2

(1.华北电力大学新能源电力系统国家重点实验室, 北京102206；2.广东电网公司电力科学研究院，广东 广州 510800)

为了分析调速系统对孤网一次调频频率响应的影响，合理调整其工作模式及参数，以孤网一次调频的频率响应特性作为研究对象，提出了一次调频评价指标。在此基础上，利用根轨迹及主导极点分析法从理论上分析了调速系统中调差系数、参与一次调频的机组比例、油动机时间常数及发电机惯性时间常数各线性环节对孤网调频性能的影响。并以孤网静态频率特性为出发点，分析了死区、调频上下限及OPC动作定值等非线性环节对调频性能的影响，提出了相应参数定量调整的方法，为孤网调速系统参数调整提供了理论依据。

孤网；一次调频；根轨迹；死区；超速保护；定量

0 引言

近年来，随着“建设坚强智能电网”概念的提出，我国电力系统呈现出“大电网、大电厂、大机组、高压输电和高度自动化智能控制”现状[1]。然而，国内仍然存在着不少孤网，其形成原因主要有以下三点：(1)联络线严重故障、极端天气或地质灾害的发生以及人为操作失误导致的与大电网的解列；(2)由于经济性等原因，拥有自备电厂的高耗能企业主动选择脱离大电网独立运行[2]；(3)主要由新能源等分布式电源构成的微电网[3-4]。

孤网运行方式相对于大型互联电网不同，负荷扰动会对孤网频率产生很大影响。文献[5-7]通过仿真实验及运行经验，指出了孤网与大电网的不同及运行需要注意的问题，定性地分析了孤网调速系统对孤网稳定的影响；文献[8-10]从汽轮机电液调速系统出发，提出改善其硬件和软件的以适应孤网运行。

总结以上文献可见：现有的研究偏向于定性分析及仿真试验，未能通过理论分析，得出适用范围广、理论性强的结论，同时没有明确指出如何修改孤网中调速器死区、一次调频限幅及OPC等定值。

本文以孤立电网一次调频原理为出发点，推导出了孤网频率响应特性传递函数。在此基础上，采用自动控制理论中的根轨迹分析法及针对高阶系统的主导极点分析法分析了参与一次调频的机组比例、调速器中的调差系数、油动机时间常数及发电机惯性时间常数对一次调频的影响。另外对非线性环节，如调速器死区、一次调频上下限和OPC(Over speed Protect Controller)保护定值对频率响应的影响进行了理论分析，同时给出了整定算式。

1 孤网频率响应传递函数的推导

调速系统主要是由调速器、发电机组(发电机与原动机)和电网环节组成。孤网没有联络线与外界联系，是一个孤立系统，对于孤立电网自身来说，其本身电气联系紧密，各节点的频率变化基本相同，因而可将其等效为单机模型进行分析。图1为其传递函数框图。

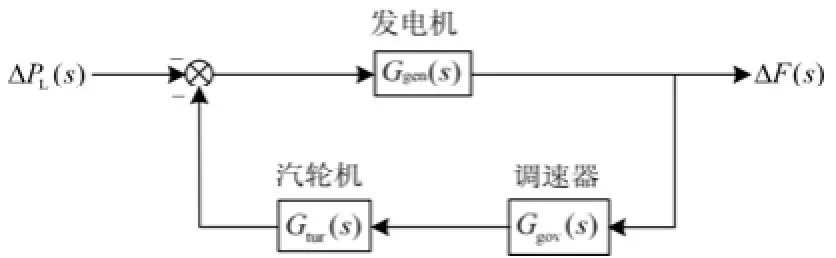
图1 孤立系统调频数学模型Fig. 1 Frequency mathematical model of isolated system

由图1可以求得孤网一次调频闭环传递函数如式(1)所示。

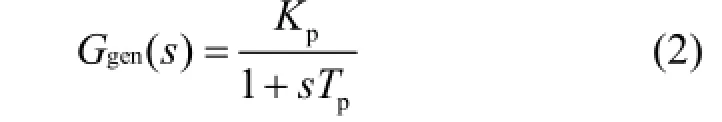
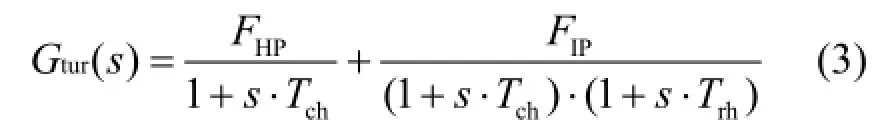
式中：chT 、rhT 分别为汽轮机蒸汽时间常数、再热时间常数；HPF 、IPF分别为高、中压缸功率分配系数；当研究经汽轮机环节的频率或功率动态响应时，低压连通管容积的影响可以忽略[12]。

调速器为调速系统工作的核心组成部分，其主要由三部分组成，速度/负载控制环节、OPC环节和执行机构，其数学模型如图2所示(简化了OPC环节)。

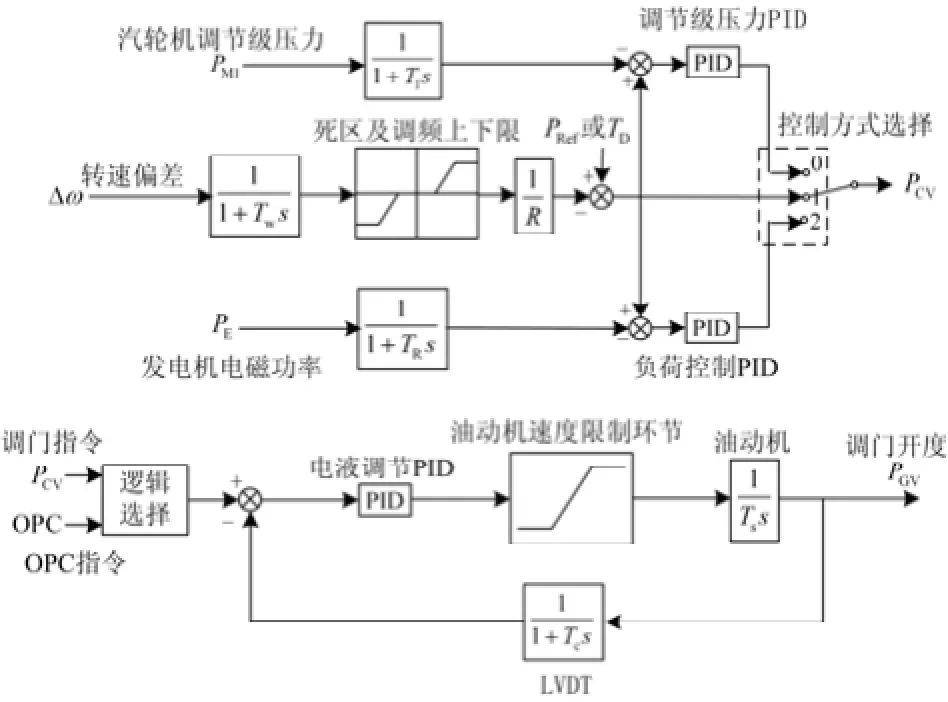
图2 调速器数学模型Fig. 2 Model of governor

图2 中上图为速度/负载控制环节，通常有3种控制方式可选择，机组和大电网并列运行时通常选择控制方式 2，即功频闭环调节。然而该控制方式不利于孤网运行，其原因是由于电磁功率的突变性和发电机转速惯性变化的矛盾，在该控制方式下，调速器会发生功率反调现象[13]，反调现象会恶化孤网频率。因而孤网运行时，采用控制方式1更合适，即转速闭环调节。

将式(2)~式(4)代入式(1)即可得出的孤网频率响应频域表达式。同时可知：频率响应与阶跃型的有功扰动量LPD (标幺值)成正比例关系，若将互联大电网看做是一个容量很大的“孤网”，则在相同有名值的有功扰动下，大电网中的LPD 将远小于孤网中的LPD 。这即是孤网频率稳定问题远比大电网严重的原因。

对于 ()F sD 的静态特性，由终值定理可知

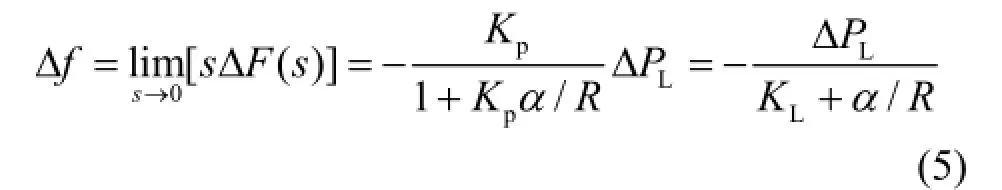
对于 ()F sD 的动态特性，由于式(1)是一个高阶多参数的表达式，难以写出其时域解析式。下文将采用根轨迹法及主导极点法分析其特性。

2 一次调频性能评价指标及分析方法

2.1 一次调频频率响应的评价指标

评价控制系统的性能从对其要求着手，即系统调节的快速性、稳定性、准确性。快速性评价指标为上升时间tr和调节时间ts，稳定性评价指标为超调量s %，准确性指标则以稳态偏差小为目标。tr、ts、s %的定义可参见文献[14]。二阶系统的性能指标tr、ts、s %由其极点位置唯一确定，其在s平面上的等值线簇如图3所示。

图3 二阶系统等tr、ts、线簇Fig. 3 Second order system contour map of tr, ts,s%

孤网一次调频频率响应普遍具有如图4所示的形式。为了评价其性能特性，以被广泛采用的控制系统性能指标为基础，取以下四个值作为调频特性衡量指标：

2) 暂态频率偏差最大值maxfD ：频率扰动过程中最大偏差值，与相对应。

3) 上升时间1t：从扰动开始到频率偏差最大所需的时间，与控制系统中的tr相对应。

4) 调整时间2t：从扰动开始到频率稳定所需的时间，与控制系统中的ts相对应。

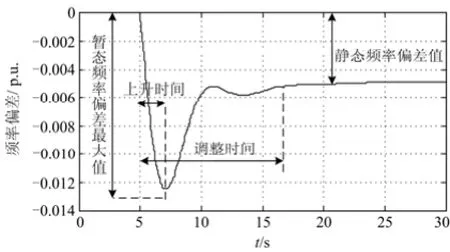
图4 一次调频频率响应曲线Fig. 4 Response curves of primary frequency regulation

2.2 根轨迹法与主导极点法

高阶系统暂态相应曲线的特点是：由一些大振荡曲线叠加上一些小振荡曲线。曲线的类型，取决于闭环极点的类型，离虚轴越近的部分，对应的分量的作用就越明显。如果存在一对共轭复数极点，它们离虚轴最近，并且其留数的模也最大，那么高阶系统的暂态相应可以用该共轭复数所决定的二阶系统来近似代替。这样的一对极点，称为闭环主导极点[14]。

对于一个具有可调参数K的闭环系统来说，如果其开环传递函数具有式(6)的形式，那么就可以利用归纳形成的绘制规则迅速准确地确定根轨迹的大致走向，即闭环极点的分布轨迹。利用这些极点的分布趋势可以迅速简洁地确定该可调参数K对系统性能的影响[14]。

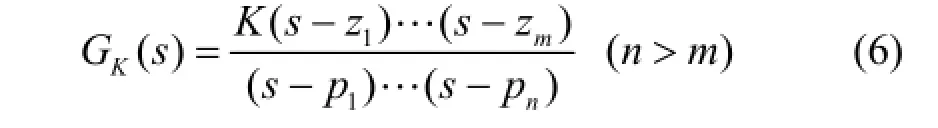
据上述理论，分析调速器线性参数对调频特性具体实施步骤如下：

(1) 选取式(2)~式(4)中的某一参数为可调参数，记作K，其余参数赋值，列写出式(1)的特征方程。

(2) 将步骤(1)中的闭环传递函数的特征方程及可调参数K整理为的形式。

(3) 设 q( s)最高次项为 sn，p ( s)最高次项为 sm，若n m> ，则构建如式(6)所示的开环传递函数，否则取 1/c K= 作为可调参数构建开环传递函数。

(4) 以步骤(3)中构建的开环传递函数绘制根轨迹，结合图3分析参数对频率响应性能的影响。

3 调速器线性参数对调频性能影响分析

式(2)~式(4)中的各项参数中调差系数R，参与一次调频的机组比例a以及调速器电液执行机构PID参数值可以自由调整。其余参数由设备本身的性能或负荷特性确定。广东某电厂的发电机组及其调速系统参数测试报告如表1所示。

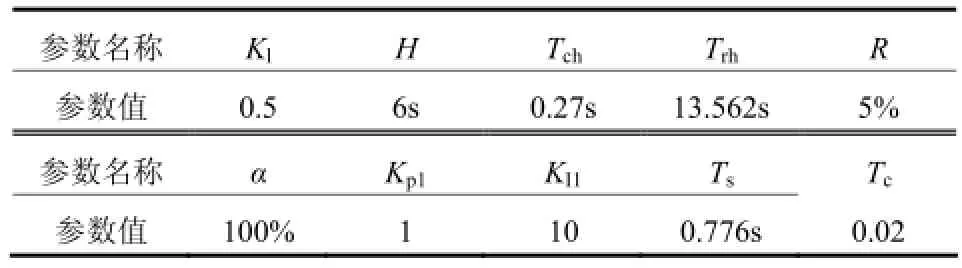
表1 调速系统参数值Table 1 Parameter values of speed control system

1) 各参数对静态频率偏差的影响。由式(5)可知，静态频率偏差 fD 与有功扰动量LPD 成正比，与成反比，且只与这四个参数相关。由于KL值很小，故在相同扰动量的情形下，是静态频率偏差的决定性因素。

2) 各参数对动态特性的影响。选取调差系数为可调参数，由本文 2.2中所述步骤，构建开环传递函数。令，得开环传递函数如下：

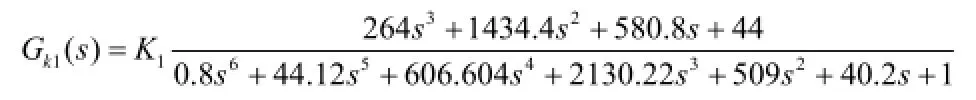
利用Matlab数学工具绘制以1K为可调参量的根轨迹如图5所示，图中箭头方向表示了1K取值由小到大时的根轨迹变化情况。

图5 为可调参数时的根轨迹Fig. 5 Root locus in setting of

图中：Gain即为1K值；Pole为1K值为Gain时的系统主导极点值；Damping为阻尼系数；Overshoot (%)为超调量s%。

同理取油动机时间常数sT和发电机时间常数H为可调参数，记，分别构建开环传递函数并绘制根轨迹如图6、图7。

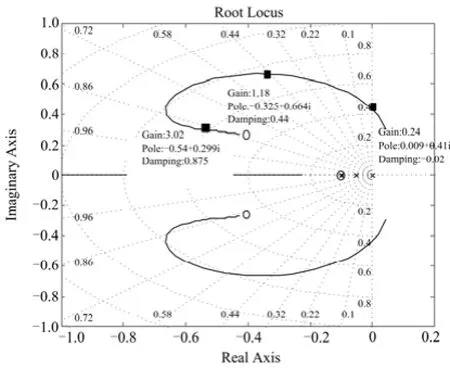
图6 s1/T为可调参数时的根轨迹Fig. 6 Root Locus in setting of s1/T

图7 1/H为可调参数时的根轨迹Fig. 7 Root locus in setting of 1/H

图5 、图6、图7三张根轨迹图中标出的靠左两点给出了相应参数的常见取值范围，与虚轴的交点为临界稳定时相应的参数值。结合等值线簇图3及表征静态频率的式(5)，可得出如表2所述结论。

表2 调速系统各参数对调频性能的影响Table 2 Impact of parameters on frequency performance

4 非线性环节对调频性能影响分析

如图8所示 Pe和分别为考虑和不考虑死区及调频上下限时的电源一次调频静态频率特性曲线，负荷静态频率特性曲线为0P，功率突增及后的曲线为1P和2P，其分别于 Pe相交于拐点处。由式(5)知电源和负荷的静态曲线的斜率绝对值分别为和LK ，LK 值很小。图中各标幺值50Hz及对应功率值为基准值。

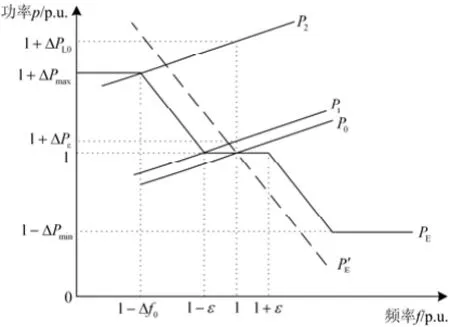
图8 静态频率特性曲线Fig. 8 Static frequency characteristic curves

4.1 非线性环节对调频性能的影响分析

1) 非线性环节对静态频率偏差的影响。

由图8可推导出在负荷突变量为LPD 时，考虑非线性环节作用下的静态频率偏差公式为

式中

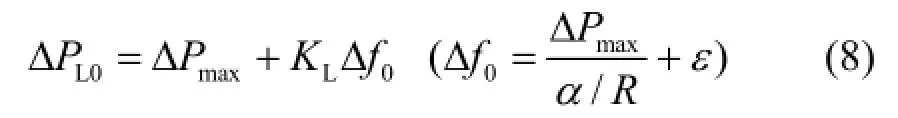
2) 非线性环节对动态特性的影响。

分析可知在孤网频率进入死区或超过一次调频上下限时，调速器会保持原动机出力不变，此时孤网频率完全依靠负荷自身的功频特性维持稳定。即死区值越大频率动态特性越差；上下限设置过小时，也会过小，小扰动下即可能有导致频率偏差急剧增大，以致稳控或频率保护装置动作，甚至可能导致系统频率崩溃[15]。

4.2 孤网中非线性环节参数定量调整理论分析

1) 死区参数的调整

由式(7)可知，死区值越大，静态频率偏差越大，动态特性越差。然而死区值并非越小越好，死区值设置过小会导致调速器的频繁动作，影响调速器寿命。由图8可推得该式给出了在死区作用下，不会导致调速器动作的最大有功突变值。死区参数值可依据该式，按照躲过孤网中最频繁的有功扰动进行整定。

2) 调频上下限的调整

一次调频上下限值设置目的是为了保证锅炉运行安全稳定，对于联网运行的机组，该值设置的较为保守。无法充分发挥锅炉的蓄热能力，不利于大扰动下孤网的频率稳定。由式(7)及图8知，时工作点为系统频率稳定临界点。考虑N-1原则，取L0PD 为孤网内的一台机组或一台负荷的功率值，由式(8)算出相应的一次调频上下限值，对该值进行校验，若满足锅炉安全稳定要求，即取该值；否则取其可能的最大值。

3) OPC保护定值的调整

为保护汽轮机组的运行安全，一般规定其转速不得超过规定转速的110%~112%，大电网中机组的OPC保护定值一般取为103%，当达到该整定值后，OPC会快速自动关闭汽门，转速下降到一定值后，OPC会再次重新打开汽门。因而，OPC动作后将会数次开合汽门，这时其便成为了网络中的“扰动源”，由于孤网没有外部功率支援，对其整体频率稳定不利[16]。孤网中OPC保护定值可按下述原则修改：

(1) 各个不同机组的OPC保护定值应当错开或采用一定的延时进行配合，避免发生所有机组OPC保护同时动作的情形。

(2) OPC保护动作的定值应当躲过L0PD 有功扰动下孤网的最高暂态频率值。该值可由实验实测或仿真计算得到。

5 结论

本文首先提出了一种分析调速器各线性环节对孤网调频特性影响的理论方法，其次分析了各非线性环节对孤网稳定的影响，提出了定量调整方法。为长期孤网运行的企业在调速系统参数调整优化提供了理论依据。这里简要总结如下：

(1) 孤网调速器应当选择转速闭环控制方式。(2) 孤网中的所有机组均应当参与一次调频，且建议调差系数选为4%，油动机性能要好。

(3) 死区、调频上下限、OPC保护定值等都应当根据孤网的实际情况进行相应调整。

[1] 张健铭, 毕天姝, 刘辉, 等. 孤网运行与频率稳定研究综述[J]. 电力系统保护与控制, 2011, 39(11): 149-154.

ZHANG Jianming, BI Tianshu, LIU Hui, et al. Review of frequency stability for isolated power system[J]. Power System Protection and Control, 2011, 39(11): 149-154.

[2] 王玉, 许和平, 王怀明, 等. 电解铝重载孤网紧急控制优化方法[J]. 电力系统自动化, 2014, 38(21): 121-126.

WANG Yu, XU Heping, WANG Huaiming, et al. Emergency control optimization measures for isolated power grid with heavy load of electrolytic aluminum[J]. Automation of Electric Power Systems, 2014, 38(21): 121-126.

[3] 张祥宇, 王慧, 樊世通, 等. 风电海水淡化孤立微电网运行与控制[J]. 电力系统保护与控制, 2015, 43(4): 25-31.

ZHANG Xiangyu, WANG Hui, FAN Shitong, et al. Operation and control of isolated microgrid with wind turbines and seawater desalination equipments[J]. Power System Protection and Control, 2015, 43(4): 25-31.

[4] 孟建辉, 石新春, 王毅, 等. 改善微电网频率稳定性的分布式逆变电源控制策略[J]. 电工技术学报, 2015, 30(4): 70-79.

MENG Jianhui, SHI Xinchun, WANG Yi, et al. Control strategy of DER inverter for improving frequency stability of microgrid[J]. Transactions of China Electrotechnical Society, 2015, 30(4): 70-79.

[5] 叶健忠, 邹俊雄, 龙霏, 等. 地区电网火电机组孤网运行频率控制策略研究[J]. 电力系统保护与控制, 2012, 40(7): 123-128.

YE Jianzhong, ZOU Junya, LONG Fei, et al. Research on frequency control strategy for isolated grid operation of thermal power unit in regional power network[J]. Power System Protection and Control, 2012, 40(7): 123-128.

[6] 黄际元, 李欣然, 曹一家, 等. 考虑储能参与快速调频动作时机与深度的容量配置方法[J]. 电工技术学报, 2015, 30(12): 454-464.

HUANG Jiyuan, LI Xinran, CAO Yijia, et al. Capacity allocation of energy storage system considering its action moment and output depth in rapid frequency regulation[J]. Transactions of China Electrotechnical Society, 2015, 30(12): 454-464.

[7] 孔繁镍, 李啸骢, 吴杰康, 等. 具有多性能指标的水轮机调速器非线性设计[J]. 电工技术学报, 2014, 29(4): 229-236.

KONG Fannie, LI Xiaocong, WU Jiekang, et al. Multiindex nonlinear controller design for hydro turbine speed governor[J]. Transactions of China Electrotechnical Society, 2014, 29(4): 229-236.

[8] 张静. DEH系统孤网运行控制系技术解决方案[J]. 热力透平, 2009, 38(1): 65-67.

ZHANG Jing. Solution for DEH system in isolated network running[J]. Thermal Turbine, 2009, 38(1): 65-67.

[9] 李俊. 火电厂单机带孤网运行的控制策略[J]. 中国电力, 2008, 41(11): 51-54.

LI Jun. Control strategy of single power unit with isolated operation in thermal power plant[J]. Electric Power, 2008, 41(11): 51-54.

[10] 周志平, 孙新良, 付晨鹏, 等. 电力系统孤网运行动态特性试验[J]. 电网技术, 2008, 32(2): 78-81.

ZHOU Zhiping, SUN Xinliang, FU Chenpeng, et al. Insular power system dynamic characteristic examination research[J]. Power System Technology, 2008, 32(2): 78-81.

[11] 杨冠城. 电力系统自动装置原理[M]. 4版. 北京: 中国电力出版社, 2007: 140-145.

[12] 于达仁, 毛志伟, 徐基豫. 汽轮发电机组的一次调频动态特性[J]. 中国电机工程学报, 1996, 16(4): 221-225.

YU Daren, MAO Zhiwei, XU Jiyu. Dynamic characteristics of primary frequency modulation turbine generation unit[J]. Proceedings of the CSEE, 1996, 16(2): 221-225.

[13] 张健铭. 小地区孤网频率稳定控制研究[D]. 北京: 华北电力大学, 2011.

[14] 孙扬声. 自动控制理论[M]. 4版. 北京: 中国电力出版社, 2007: 78-83, 189-192.

[15] 滕予非, 张华, 汤凡, 等. 偏远地区小电网与主网解列后高频高压风险及抑制策略[J]. 电力系统保护与控制, 2015, 43(1): 129-136.

TENG Yufei, ZHANG Hua, TANG Fan, et al. Overfrequency and over voltage risk of isolated small power grid in remote area and its suppression strategy[J]. Power System Protection and Control, 2015, 43(1): 129-136.

[16] 陈兴华. 基于安全自动装置控制的火电机组改进超速保护[J]. 电力系统保护与控制, 2015, 43(1): 150-154.

CHEN Xinghua. Improved OPC by automatic-security device[J]. Power System Protection and Control, 2015, 43(1): 150-154.

(编辑 张爱琴)

Analysis on quantitative parameter adjustment of speed governor in isolated power grid

LI Fei1, XIAO Shiwu1, WANG Cong1, XIAO Xiaoqing2, ZHENG Likun2
(1. State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources, North China Electric Power University, Beijing 102206, China; 2. Electric Power Research Institute of Guangdong Grid, Guangzhou 510800, China)

In order to analyze the impacts that speed governor system has on the primary frequency regulation in isolated power grid, based on the frequency response characteristic, evaluation index for primary frequency regulation is proposed. And the influence on the primary frequency regulation by governor static difference coefficient, the ratio of generator participating in primary frequency regulation, the generator inertia time constant, and the governor time constant is analyzed by using root locus and predominant pole. The function of dead band, first frequency modulation limit and OPC (over-speed protection control) is argued. Meanwhile, based on static frequency characteristic curves, and methods for quantitative parameter adjustment are proposed. This work is supported by National Key Basic Research Program of China (973 Program) (No. 2012CB215200).

isolated power grid; primary frequency regulation; root locus; dead band; OPC; quantitative

2015-11-04；

2016-01-27

李 飞(1991-) ，男，通信作者，硕士研究生，主要研究方向为电力系统运行分析与控制；E-mail: 1045278574@ qq.com

肖仕武(1974-)，男，博士，副教授，主要研究方向为电力系统运行分析与控制、电力系统故障分析与继电保护；E-mail: xiaoshiwu@263.net

王 琮(1989-)，女，硕士，主要研究方向为电力系统运行分析与控制。

10.7667/PSPC151940

国家重点基础研究发展计划项目(973项目) (2012CB215200)