基于罗德里格矩阵的空间坐标转换

韩梦泽，李克昭

(1.河南理工大学 测绘与国土信息工程学院，河南 焦作 454003；2.商丘工学院 土木工程学院，河南 商丘 476000)



基于罗德里格矩阵的空间坐标转换

韩梦泽1,2，李克昭1

(1.河南理工大学 测绘与国土信息工程学院，河南 焦作 454003；2.商丘工学院 土木工程学院，河南 商丘 476000)

摘要：三维坐标转换一直是测量领域的一个重要内容。针对现有算法普遍存在的不适用大旋角转换、计算繁杂等缺点，从旋转矩阵的表达方式入手，提出了一种基于罗德里格矩阵的三维坐标转换方法。算例分析表明,文中方法无需线性化，计算简便，且能适用大旋角转换。

关键词：坐标转换；旋转参数；罗德里格矩阵

不同空间直角坐标系之间的坐标转换一直是测绘领域的一个重要内容，国内外很多学者在这方面做了大量研究[1-5]。空间坐标转换的实质是用公共点的2套坐标和非公共点的1套坐标推估非公共点的另1套坐标。坐标转换过程通常分2步，先由公共点坐标解算转换参数，再由转换参数转换非公共点。转换参数通常分为旋转、平移和尺度参数，其中旋转参数的确定是坐标转换的核心。传统的三维坐标转换模型是用3个旋转角作为旋转参数，建立的模型是非线性的，常需要用泰勒级数展开的方法将模型线性化，计算比较繁杂[6-8]。在小角度旋转情况下，可对旋转矩阵作近似处理，得到线性模型，如常用的布尔莎模型[9]。针对大旋角的坐标转换问题，陈义提出了一种用9个方向余弦参数作为旋转参数的解算模型，虽然能适用大旋角转换，但参数个数达到了13个[10]。游为直接从三维直角坐标转换的非线性方程出发，根据最优化问题的极值条件，采用基于同伦连续思想的Li-Yorke算法求解7个转换参数，虽然能适用大旋角转换，但计算较复杂[11]。针对这些情况，本文提出了一种用罗德里格矩阵表示旋转矩阵的坐标转换方法，仅有3个旋转参数，计算过程无需线性化，且能适用大旋角转换。

1空间坐标转换的数学模型

设A点在空间直角坐标系o-uvw和o-xyz中的坐标分别为(u,v,w)和(x,y,z);a1,a2,a3为轴u与轴x,y,z间夹角的余弦;b1,b2,b3为轴v与轴x,y,z间夹角的余弦;c1,c2,c3为轴w与轴x,y,z间夹角的余弦;λ为尺度参数;(Δx,Δy,Δz)为平移参数，则有如下关系：

(1)

方向余弦矩阵通常由绕3个坐标轴顺次旋转的欧拉角φ,ω,κ表示，这时需要求取的转换参数为λ,φ,ω,κ,Δx,Δy,Δz。

2基于罗德里格矩阵的三维坐标转换模型

2.1罗德里格矩阵

罗德里格矩阵可由反对称矩阵构建，引入一个具有3个独立元素的反对称矩阵

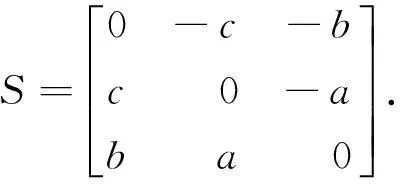
则R=(I+S)(I-S)-1是个正交矩阵，其中I是3阶单位阵。

将R展开为

(3)

这个正交矩阵就是罗德里格矩阵。

2.2转换参数的求解

用罗德里格矩阵表示方向余弦矩阵时，需要求取的转换参数为λ,a,b,c,Δx,Δy,Δz。参数解算过程可分3步，先求尺度参数，再求旋转参数，最后求平移参数。尺度参数可由2个公共点在不同坐标系下的距离之比算出，其表达式为

(4)

公共点较多时，可求出各点间多个距离比，再取平均值。

在解算旋转参数a,b,c时，可以先消去平移参数，将2个公共点的坐标代入式(1)，求差得

(5)

上式两端同时左乘(I-S)得

(6)

由R=(I+S)(I-S)-1知(I-S)R=(I+S)，将其代入式(6)得

(7)

将I和S代入，整理得

(8)

式中:u21=u2-u1，v21=v2-v1，w21=w2-w1，x21=x2-x1，y21=y2-y1，z21=z2-z1。

这个方程组左边的系数矩阵为奇异阵，3个方程里仅有2个独立，需要至少2个这样的方程组才能解算出a,b,c，也就是至少需要3个公共点。当有n个公共点时，可列出(n-1)个形如上式的方程组，共有3(n-1)个方程，其总误差方程为

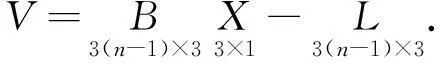
式中:

按最小二乘法间接平差原理求解未知数

(10)

计算出a,b,c后，即可求出旋转矩阵，然后按下式求解平移参数：

(11)

3算例分析

为验证上文算法的适用性，现用一组模拟数据进行计算分析。空间坐标转换的核心是确定旋转参数，尺度参数和平移参数的求取是很简单的，为了更简明的验证本文的算法，这里将尺度参数设为1，将3个平移参数都设为0。目标坐标系与原坐标系间坐标轴按Y轴、X轴、Z轴的顺序旋转，旋转角度依次为2°、4°和6°，则旋转矩阵为

设3个点在原坐标系中的坐标分别为(5,8,15)、(10,10,10)、(20,30,40)，则由旋转矩阵可计算出其在目标坐标系下的坐标为(3.591 0,7.411 8,15.689 8)、(8.519 6,10.266 2,11.046 4)、(15.274 1,29.058 2,42.688 7)。由这3个点的2套坐标，用上文的算法计算出的罗德里格参数a,b,c分别为0.034 0、0.019 3、0.053 0，罗德里格矩阵为

可见，R2与R1相差极小，仅有3个方向余弦值不同，且都是相差0.000 1。需要指出的是，用MATLAB计算数值，默认的显示精度是到小数点后4位，当显示精度设置为更高时，R2与R1的差值会更小。

上面的算例是小角度旋转的情况，为了更好地验证本文算法的适用性，现再模拟一组大角度旋转下的数据。坐标轴的旋转顺序不变，旋转角度依次为20°、40°和60°，则旋转矩阵为

设3个点在原坐标系中的坐标分别为(5,8,15)、(10,10,10)、(20,30,40)，则由旋转矩阵计算出的其在目标坐标系下的坐标为(-9.922 5,-3.260 6,14.314 7)、(-9.062 7,4.036 5,14.197 7)、(-32.602 7,-0.952 6,42.850 4)。由这3个点的2套坐标，用上文的算法计算出的罗德里格参数a,b,c分别为0.272 3、0.401 3、0.666 2，旋转矩阵为

可见，R4与R3相差极小，仅有2个方向余弦值不同，且都是相差0.000 1。由以上算例分析可知，本文的模型是正确的，可用于小角度和大角度旋转的坐标转换，且转换精度很高。

4结束语

本文从旋转矩阵的表达方式入手，用罗德里格矩阵表示方向余弦矩阵，推导了基于罗德里格矩阵的三维坐标转换模型。与常规的坐标转换模型相比，该模型用代数运算替代了三角运算，无需对旋转参数线性化，模型简单，计算简便，可用于大旋角的坐标转换，且具有很高的转换精度。

参考文献：

[1]王解先,王军,陆彩萍.WGS-84与北京54坐标的转换问题[J].大地测量与地球动力学,2003,23(3):70-73.

[2]田桂娥,宋利杰,尹利文.地方坐标系与CGCS2000坐标系转换方法的研究[J].测绘工程,2014,23(8):66-69.

[3]李博峰,沈云中,李微晓.无缝三维基准转换模型[J].中国科学:地球科学,2012,42(7):1047-1054.

[4]刘毅,岳建平,卢银宏,等.补偿最小二乘法在大地坐标转换中的应用[J].测绘工程,2012,21(5):80-82.

[5]段鹏硕,刘根友,龚有亮,等.空间坐标系变换的函数梯度描述方法[J].测绘学报,2014,43(10):1005-1012.

[6]张卡,张道俊,盛业华,等.三维坐标转换的两种方法及其比较研究[J].数学的实践与认识,2008,38(23):121-128.

[7]许文学,王保丰,羊远新,等.坐标系转换参数初值快速计算的新方法[J].测绘工程,2010,19(4):4-7.

[8]潘国荣,周跃寅.两种坐标系转换计算方法的比较[J].大地测量与地球动力学,2011,31(3):58-62.

[9]鲍建宽,李永利,李秀海.大地坐标转换模型及其应用[J].测绘工程,2013,22(3):56-60.

[10] 陈义,沈云中,刘大杰.适用于大旋转角的三维基准转换的一种简便模型[J].武汉大学学报(信息科学版),2004,29(12):1101-1105.

[11] 游为,范东明,黄瑞金.适用于任意旋转角的三维直角坐标转换方法[J].测绘科学,2009,34(5):154-155.

[责任编辑：刘文霞]

Spatial coordinate transformation based on Rodrigues matrix

HAN Mengze1,2,LI Kezhao1

(1.School of Surveying and Land Information Engineering,Henan Polytechnic University,Jiaozuo 454003,China；2.College of Civil Engineering,Shangqiu Institute of Technology,Shangqiu 476000,China)

Abstract：The three-dimensional coordinate transformation has always been an important content in the field of surveying and mapping.The existing algorithms are usually difficult to calculate or can’t adapt to big angle rotation transformation.The transformation model based on Lodrigues matrix was deducted.Numerical examples show that the method is feasible and simple,which needn’t linearization and can adapt to big angle rotation transformation.

Key words：coordinate transformation；rotation parameters；Rodrigues matrix

中图分类号：P226+.3

文献标识码：A

文章编号：1006-7949(2016)04-0025-03

作者简介：韩梦泽(1988-)，男，硕士.

基金项目：国家自然科学基金资助项目(41272373，41202245)

收稿日期：2015-01-03