一类半向量二层规划问题乐观最优解的求解方法

王思, 吕一兵　(长江大学信息与数学学院,湖北 荆州 434023)



一类半向量二层规划问题乐观最优解的求解方法

王思, 吕一兵(长江大学信息与数学学院,湖北 荆州 434023)

[摘要]研究了上层为分式规划、下层为线性多目标规划的一类半向量二层规划问题乐观最优解的求解方法。利用对偶理论, 先将半向量二层规划问题转化为相应的单层优化问题, 同时取下层问题的对偶间隙与上层目标函数分母的比值作为罚项, 构造了该类半向量二层规划问题的罚问题, 最后基于罚问题的相关性质设计了一种求解算法。数值试验表明, 所设计的算法是可行的。

[关键词]半向量二层规划；线性分式；罚函数；乐观最优解

二层规划包含上下2层, 上层和下层都有各自的目标函数和约束条件, 其中上层是以下层决策变量为参数, 而下层又受制于上层决策变量的复合优化问题[1]。由于二层规划能够恰当的描述实际问题中存在的层次关系, 因此被广泛的应用于非平衡经济市场竞争、资源分配、交通网络、环境保护以及工程设计[2～5]等问题，其相关理论也受到越来越多的国内外学者的关注[6，7]。二层规划的数学模型可以表述为:

(1)

其中, x∈Rn；y∈Rm；F:Rn×Rm→R；H：Rn×Rm→Rk；h:Rn×Rm→Rr。

当上层是一个标量优化问题, 下层是一个向量优化问题时, 相应的二层规划被称为半向量二层规划问题。Bonnel和Morgan[8]分析了下层为凸向量优化时解的最优性必要条件,并给出了求解这类问题的一种精确罚函数方法。 Zheng和Wan[9]设计了包含2个不同罚因子的精确罚函数方法来求解半向量二层规划问题, 然而, 由于算法中包含2个罚参数,求解时的计算量较大。任爱红和王宇平[10]针对这类问题, 先将其转化为单层优化问题, 同时提出了转化问题的偏静态条件定义, 并在此基础上构造了半向量二层规划的精确罚问题。吕一兵和万仲平[11]针对线性半向量二层规划问题, 将其转化为有限个线性规划问题, 并得到了这类问题的全局最优解。

受上述文献的启发, 笔者将考虑上层为线性分式单目标, 下层为线性多目标的一类半向量二层规划问题：首先, 利用对偶规划理论, 给出下层问题的对偶间隙； 然后, 考虑对偶间隙与上层目标函数分母的比值作为罚项, 构造了这类半向量二层规划问题的罚问题, 最后基于罚问题的相关性质设计了一种求解算法。

1模型及定义

考虑如下半向量二层规划问题, 其具体数学模型表述如下：

(1)

其中， M(x)为如下线性多目标规划问题：

(2)

的弱有效解集； x∈Rn；y∈Rm；a1,a2∈Rn；b1,b2∈Rm；C∈Rl×m；A∈Rp×n；B∈Rp×m；b∈Rp,X={x|x≥0}。

定义1集合S1={(x,y)|Ax+By≤b,y∈M(x)}表示问题(1)的可行域。若点(x,y)∈S1,则称(x,y)为问题(1)的可行解。

定义2(x*,y*)∈S1为问题(1)的全局最优解, 如果对于任意的(x,y)∈S1, 有F(x*,y*)≤F(x,y)。

注1在问题(1)中, 由于下层为多目标规划问题, 因此, 对于给定的上层决策变量,下层问题的最优解一般是不唯一的． 对于下层有不唯一最优解的二层规划问题, 其最优解的定义一般采用乐观最优解或悲观最优解[12]。笔者考虑采用乐观最优解的定义。

在下面的研究中，假设如下条件成立：

(A1)约束域S={(x,y)|Ax+By≤b,x≥0,y≥0}以及集合X均为非空紧集。

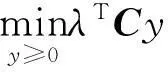
s.t.Ax+By≤b

问题(1)可转化为：

(3)

利用线性规划的对偶理论, 得到问题(3)的下层对偶问题为：

(4)

其中， ϖ∈Rp(行向量)为对偶变量。

记W={ϖ|-ϖB≤λTC, ϖ≥0}, 对偶间隙π(x,y,λ,ϖ)=λTCy+ϖb-ϖAx，关于问题(1)和问题(3)最优解的关系, 有以下结果。

定理1假设条件(A1)成立,(x*,y*,λ*)为问题(3)的最优解, 当且仅当存在ϖ*∈W, 使得(x*,y*,λ*,ϖ*)为如下问题：

(5)

的最优解, 同时(x*,y*)为问题(1)的最优解。

证明由对偶理论可知, 一定存在ϖ*∈W, 使得ϖ*为问题(5)的最优解。对于固定的(x*,λ*)且满足λTCy+ϖb-ϖAx=0, 则y*为下层问题的最优解, 故(x*,y*)也是问题(1)的最优解。

2主要结果

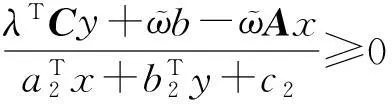
(6)

其中,μ∈R+是罚参数；(x,y,λ,ϖ)∈S×U。

关于问题(5)和问题(6)最优解之间的关系, 有下面的结果。

引理1若(xμ,yμ,λμ,ϖμ)是问题(6)的最优解, 并且它也是问题(5)的可行解, 则它也是问题(5)的最优解。

对于给定的(λ，ϖ)∈U及μ∈R+, 定义：

有以下定理成立。

定理2假设条件(A1)成立, 则问题：

的最优解(λ*,ϖ*)一定在其多面体的极点处取得。

证明首先证明φμ(λ,ϖ)是凹函数。取集合U中任意2点(λ1,ϖ1),(λ2,ϖ2)，η∈(0,1), 则有：

φμ(η(λ1,ϖ1)+(1-η)(λ2,ϖ2))

=ηφμ(λ1,ϖ1)+(1-η)φμ(λ2,ϖ2)

故φμ(λ,ϖ)为凹函数。又由于集合U为多面体, 则在多面体约束条件下的极小化凹函数,其最优解一定在U的极点处取得。

定理3假设条件(A1)成立, 则问题(6)的最优解(x*,y*,λ*, ϖ*)∈SE×UE。

证明若(x*,y*)为问题(1)的最优解, 则一定存在(λ*,ϖ*)∈U, 使得：

又由于(xμ,yμ,λμ,ϖμ)是问题(6)的最优解, 则有：

即：

3算法设计

根据上述性质, 笔者设计一种求解问题(6)的算法，算法描述如下：

步1选取初始值μ>0及δ>0。

步2利用线性规划技术求得多面体U的所有顶点, 记为UE={u1,u2,…,ut}, 令i=1。

步3求解下面的问题P(λi,ϖi)：

(7)

求得最优解为(xi,yi)。

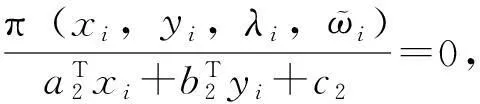
注2该算法需要求出下层对偶问题可行域多面体U的全部顶点, 即UE, 这是算法实现的关键点之一, 求解多面体顶点方法可参考文献[16]。

定理6上述算法所得到的解为问题(1)的最优解。

证明由定理1以及引理1, 定理6显然成立。

4数值试验

为了说明上述算法的可行性, 考虑以下线性分式半向量二层规划问题[14]：

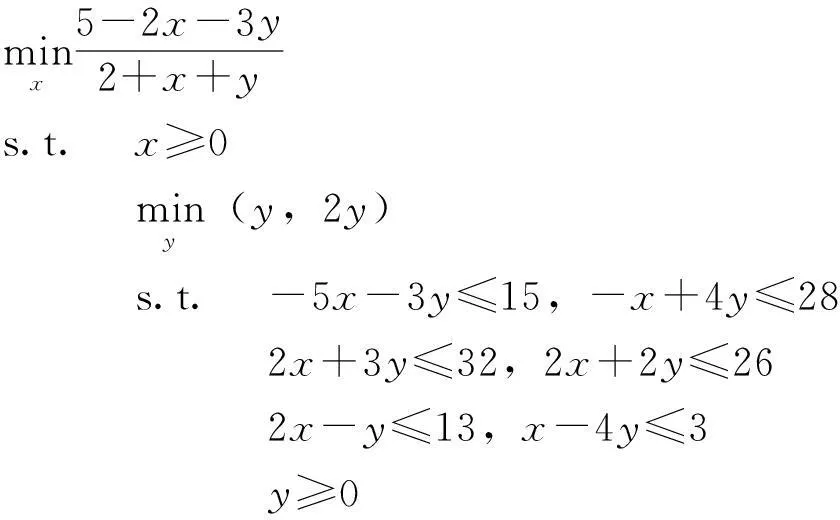
(8)

图1表示原问题(8)的约束域和可行域, 当上层固定一个决策变量x, 下层问题y的取值如虚线所示。

上述算例中下层问题的对偶问题为：

则：

U={(λ,ϖ)∈R2+6|λ1+λ2=1,3ϖ1-4ϖ2-3ϖ3-2ϖ4+ϖ5+4ϖ6≤λ1+2λ2,λ≥0,ϖ≥0}

其顶点为:

(λ2,ϖ2)=(1,0,0,0,0,0,1,0)

表1　不同顶点所对应的最优解

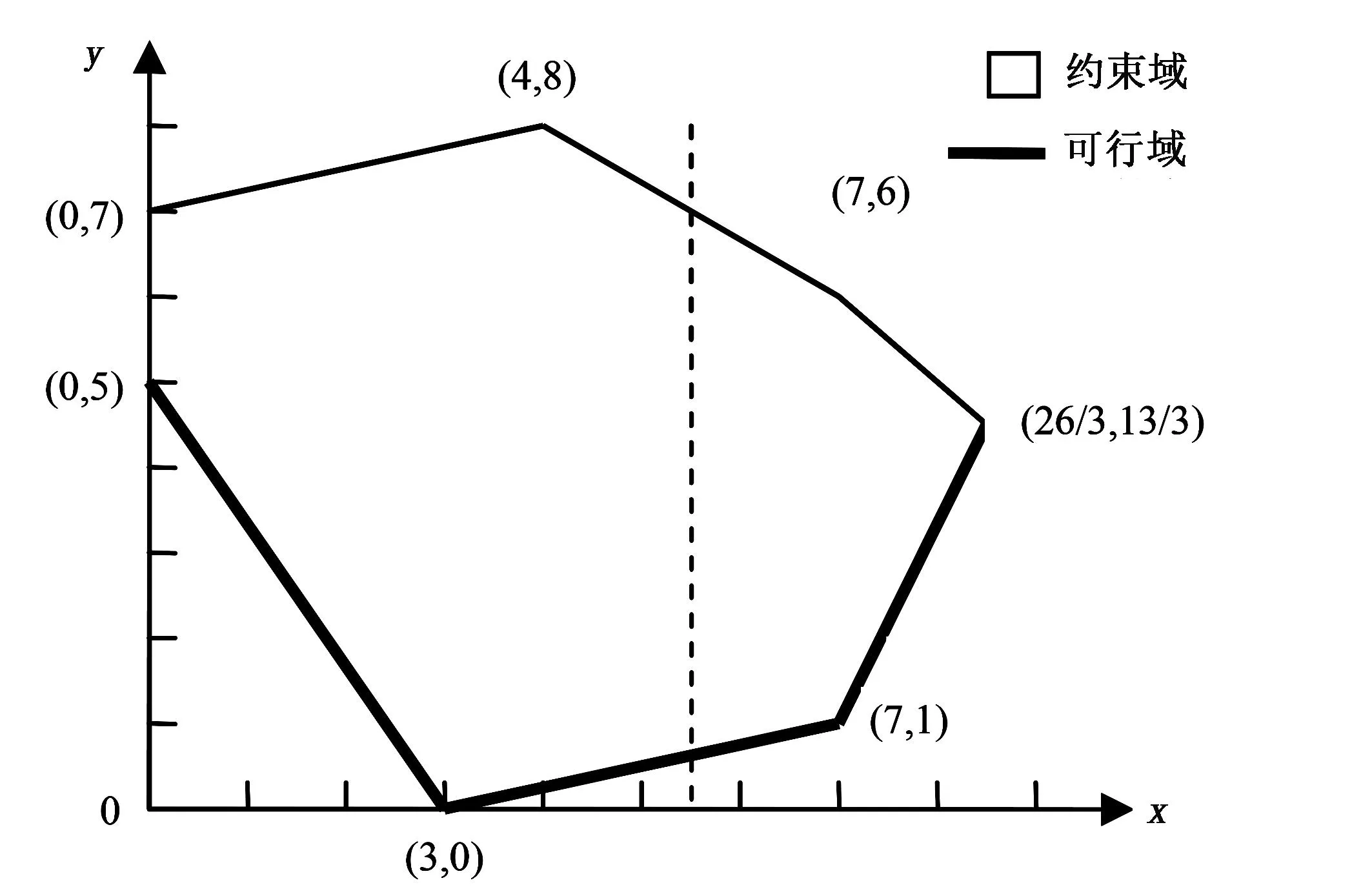
图1　原问题(8)的约束域和可行域

5结语

研究了一类线性分式半向量二层规划问题乐观最优解的求解方法, 利用对偶理论,将其转化为单层优化问题, 同时取下层问题的对偶间隙与上层目标函数分母的比值作为罚项, 构造了线性分式半向量二层规划的罚问题, 基于罚问题的相关性质设计了一种求解算法。数值结果表明, 所设计的算法是可行的。值得说明的是, 由于分式半向量二层规划是个比较复杂的问题, 笔者只讨论了上层为线性分式的情况, 进一步将针对上层为非线性分式讨论其最优解的取值情况。

[参考文献]

[1]滕春贤,李智慧. 二层规划的理论与应用[M].北京: 科学出版社,2002.

[2]GaoZiyou,SunHuijun,ZhangHaozhi.Agloballyconvergentalgorithmfortransportationcontinuousnetworkdesignproblem[J].OptimizationandEngineering,2007,8(3): 241～257.

[3]ErhanErkut,FatmaGzara.Solvingthehazmattransportnetworkdesignproblem[J].ComputersOperationsResearch,2007,35: 2234～2247.

[4]吕一兵,万仲平,胡铁松.水资源优化配置的双层规划模型系统工程理论与实践[J].2009,29(6):115～120.

[5]刘娟娟,范炳全,祝炳发. 双层规划在城市交通污染控制中的一个应用[J]. 管理工程学报,2005(4):87～90.

[6]王广民,万仲平,王先甲. 二(双)层规划综述 [J].数学进展,2007,36: 513～529.

[7]ColsonB,MarcotteP,SavardG.Anoverviewofbileveloptimization[J].AnnalsofoperationsResearchannals,2007,153(1): 235～256.

[8]BonnelH,MorganJ.Semivectorialbileveloptimizationproblem:Penaltyapproach[J].JournalofOptimizationTheoryandApplications,2006,31(3): 365～382.

[9]ZhengY,WanZ.Asolutionmethodforsemivectorialbilevelprogrammingproblemviapenaltymethod[J].JournalofAppliedMathematicsandComputing, 2011,37: 207～219.

[10]任爱红,王宇平. 求解半向量双层规划问题的精确罚函数法 [J].系统工程理论与研究,2014,34(4): 910～916.

[11]吕一兵,万仲平. 线性半向量二层规划问题的全局优化方法 [J].运筹学学报,2015,19(2): 29～36.

[12]DempeS.Foundationsofbilevelprogramming[M].London:KluwerAcademicPublishers,2002.

[13]LvY,WanZ.Asolutionmethodfortheoptimisticlinearsemiveetorialbileveloptimizationproblem[J].JournalofInequalitiesandApplications,2014: 164.

[14]PedroCerbuna.Apenaltymethodforsolvingbilevellinearfractional/linearprogrammingproblems[J].Asia-PacificJournalofOperationalResearch,2004,207～224.

[15]BazaraaMS,SheraliHD，ShettyCM.NonlinearProgramming:TheoryandAlgorithms[M].2nded.NewYork:JohnWileyandSons,1993.

[16]MatheissRH,RubinDS.Asurveyandcomparisonofmethodsforfindingallverticesofconvexpolyhedralsets[J].MathernaticsofOperations,1980,5(2): 167～185.

[编辑]张涛

[文献标志码]A

[文章编号]1673-1409(2016)01-0001-06

[中图分类号]O224

[作者简介]王思(1990-)，女，硕士生，现主要从事最优化理论与算法方面的研究工作。[通信作者]吕一兵(1979-)，男，博士，副教授，现主要从事最优化理论与算法方面的教学与研究工作；E-mail:lvyibing_2001@sohu.com。

[基金项目]国家自然科学基金项目(11201039)。

[收稿日期]2015-10-15

[引著格式]王思, 吕一兵.一类半向量二层规划问题乐观最优解的求解方法[J].长江大学学报(自科版)，2016,13(1)：1～6.