一种基于图像单应性矩阵的投影仪标定方法

李宝顺，顾春霞，包亚萍，李义丰

（南京工业大学电子与信息工程学院，江苏南京 211816）



一种基于图像单应性矩阵的投影仪标定方法

李宝顺，顾春霞，包亚萍，李义丰

（南京工业大学电子与信息工程学院，江苏南京 211816）

摘 要：投影仪标定是计算机视觉的关键技术之一，针对实际应用中摄像机和投影仪相对位置关系，提出一种基于摄像机和投影仪图像单应性矩阵的投影仪标定方法.对捕获的图像进行背景差分、特征点提取等操作得到投影图像和摄像机图像之间的单应性矩阵，进而获得投影仪参数矩阵，完成投影仪标定.经实验论证，该方法操作简单，反投影像素误差在0.3到1个像素之间，证明了该方法的有效性.

关键词：投影仪标定；相对位置关系；特征点提取；单应性矩阵；反投影误差

对投影仪进行标定获取投影仪内外参数是光栅投影研究领域关键技术之一［1-2］.传统的投影仪标定方法将投影仪标定视为摄像机标定逆过程，该类方法先对摄像机进行标定，然后利用标定好的摄像机获取投影图像特征点的坐标对投影仪进行标定，该类方法操作简单，但需要利用标定好的摄像机获取投影图像特征点坐标，因而在投影仪标定过程中不可避免引入摄像机标定的误差［1］，使其标定精度降低，难于应用于精度要求高的场合.近年来有学者采用投射一定规律的结构光［3-7］来标定投影仪，该类方法核心思想是投影一定规律的结构光到投影平面上，利用结构光的已知信息对投影仪进行标定，该方法精确度可较高，但其精度受图像特征点的提取影响，可使该类方法可靠性降低.针对上述问题，作者提出一种基于摄像机和投影仪图像单应性矩阵的投影仪标定方法，利用投影仪和摄像机之间的位置关系，得到摄像机图像与投影仪图像之间的确定关系，构建由伪随机编码构建的投影图像.该图像的特征点容易获取，有效地标定了投影仪，提高了投影仪标定的精度.

1　投影仪标定原理

摄像机和投影仪相互之间位置固定，投影仪图像与摄像机图像之间存在确定关系.摄像机投影仪系统如图1所示.

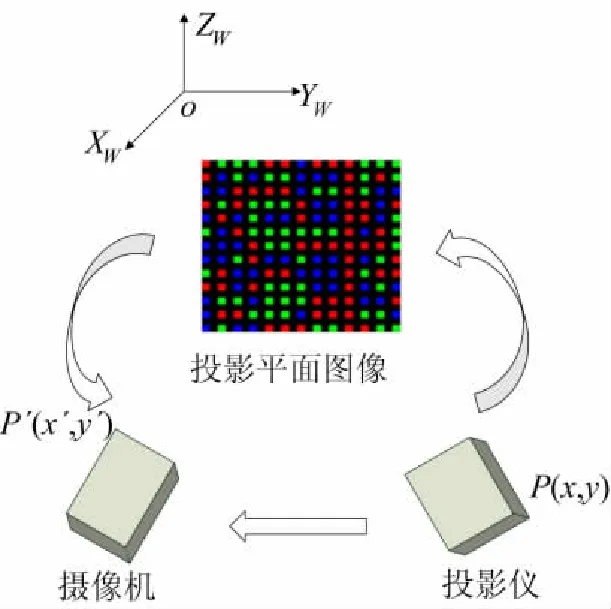
图1　摄像机投影仪系统Fig.1　Diagram of camera-projector system

1.1 投影仪单应性矩阵获取

小孔成像原理为公认的摄像机成像模型，其光学模型为针孔模型.投影仪的功能与摄像机相反而光学结构相同，故摄像机和投影仪均采用针孔模型.摄像机投影仪系统模型如图2所示.

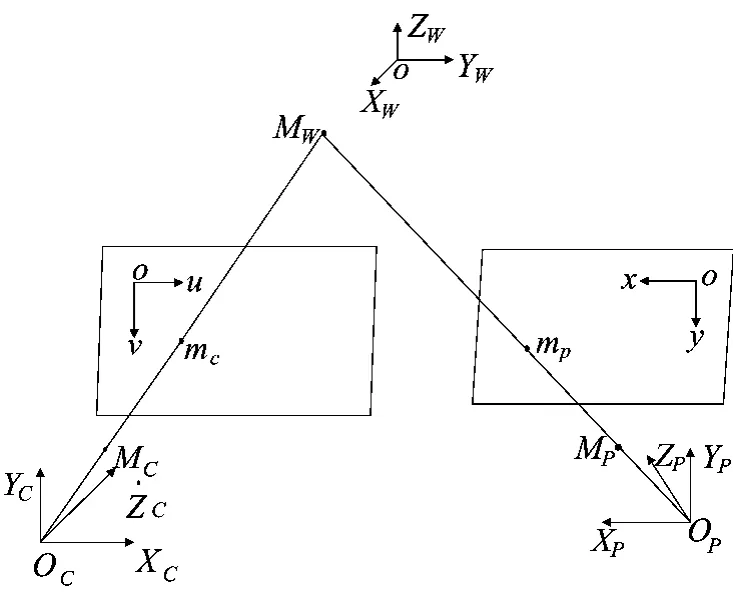
图2　摄像机投影仪系统成像模型Fig.2　Camera-projector system imaging model

图2中，世界坐标系为XWYWZW，投影仪坐标系为XPYPZP，摄像机坐标为XcYcZc，以摄像机为列描述成像模型，空间某点世界坐标为MW（X，Y，Z），齐次坐标表示为M～W＝［X，Y，Z，1］，它在摄像机图像平面上成像为点mc（u，v），记它的齐次坐标为m～c＝［u，v，1］，则空间点世界坐标到图像像素点坐标的齐次变换关系为

记Hc＝Ac［Rctc］，sc为比例因子，Rc和tc分别为世界坐标系相对于摄像机坐标系的旋转矩阵和平移矢量，Ac为摄像机内部参数矩阵，可表示为

投影仪和摄像机光学模型一致，则投影仪图像像素点坐标和空间点世界坐标之间有以下的齐次变换关系式

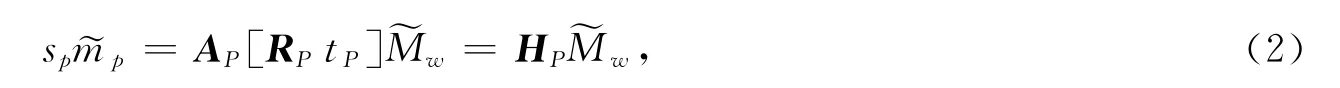
其中：HP＝AP［RPtP］，sP为比例因子，AP为投影仪内部参数矩阵，RP和tP分别为世界坐标系相对于投影仪坐标系的旋转矩阵和平移矢量，且αP＝f／dx，βP＝f／dy，f为投影仪焦距，dx为单位像素在水平的物理长度，dy为单位像素在垂直方向的物理长度，（x0，y0）为主点坐标，s2为水平单位像素和垂直单位像素的倾斜因子.HP是可逆的，由式（2）变换可得

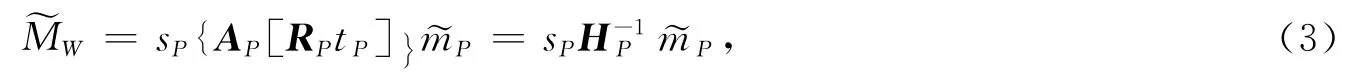
将式（3）代入式（1），则摄像机图像像素点坐标和投影仪图像像素点坐标之间的转换关系如下式所示

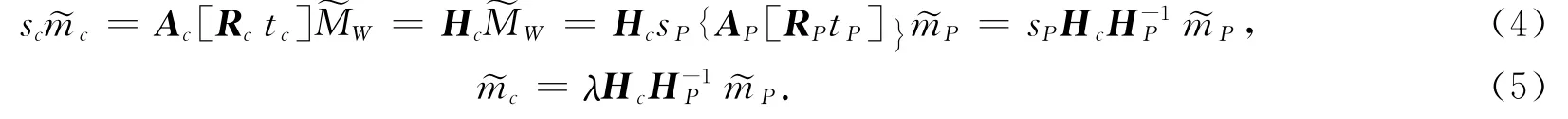
将HcH-1P记为H，Hc和H-1P都为3×3的矩阵，由矩阵性质可知H也为3×3矩阵，式（5）可以转换为下式

H矩阵即为投影仪图像和摄像机图像之间的单应性矩阵，则

分解HP可得到投影仪的内参和外参.

1.2 H矩阵求解

式（6）的H矩阵即投影仪图像和摄像机图像之间的单应性矩阵，把H表示为，由式（6）可得m～c和Hm～P是共线的，则

而

故（8）式可转化为下式

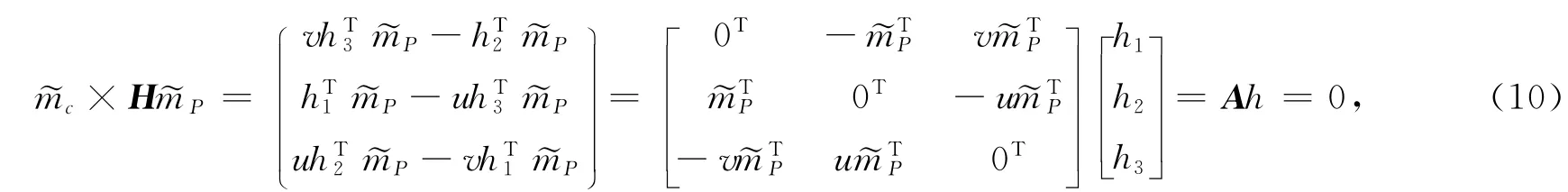
式（10）中有两个方程是线性相关的，取其中两行将式（10）化为

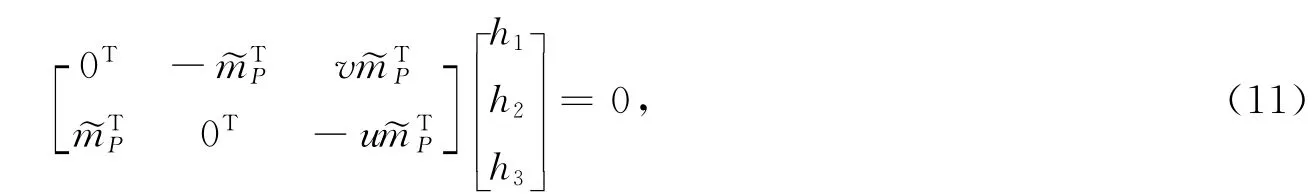
若n对对应点，则可以得到n对类似（11）的方程，对其进行整理可得到以下方程组

令h33＝1，h的自由度为8，每对对应点可以得到2个方程，可将4个点的坐标对代入式（12）求得H.

2　投影仪标定方法

对投影仪进行标定，需得到投影图像特征点的坐标来确定投影仪和摄像机的单应性矩阵.投影由伪随机编码生成色块图案，该图像色块变化具有唯一性，容易识别，可以方便得到图像特征点坐标.

2.1 伪随机编码投影图案

投影图案采用伪随机编码［8-9］产生投影模板.伪随机编码是一个预先确定并可重复实现的序列，产生的序列可表示成伪随机阵列的形式.它有良好的窗口特性，用伪随机编码对投影仪图像进行编码，可保证窗口获得的每个色块区域都是唯一的，可以容易判断该色块区域在整个投影图像中的位置及识别特征点.

伪随机编码采用离散方形编码［10］，方形编码每个色块都有4个角点，较别的编码图像有更多的特征点，且每个色块都是独立的，方便特征点位置的确定.

论文采用q＝3，k1＝3，k2＝3的伪随机序列，该伪随机序列的周期为n＝qm-1＝19 682，本原多项式为x9＋x7＋x2＋x＋1，检测窗口大小为3×3，该序列足以产生投影仪标定图像所需的色块，选取其中一部分子阵列作为投影模板，记选取的阵列的3种基元分为0，1，ξ，指定0为绿色，1为红色，ξ为蓝色.每一个矩阵元素设置为20×20像素的正方形，每个正方形之间的间距设置为20像素.因为黑色容易和其他颜色区分，设置背景色为黑色，得到伪随机编码的投影图案如图3所示.

图3　伪随机编码投影图案Fig.3　Pseudo-random coding projection pattern

2.2 图像背景差分和色块颜色判断

摄像机捕获到的图像因为周围环境噪声、投影面可能存在纹路之类的影响，对色块中心坐标提取有一定干扰，需要在提取中心坐标前，对捕获的图像进行处理，减小不必要的干扰.在投影伪随机编码图案前，投影一副全黑的图像，作为背景差分的背景图案.将投影图像和背景图像分离开，可以降低外部因素对投影图像的影响.经过背景差分后的图像记为I′（u，v）（R，G，B），处理后的图像可由下式表示

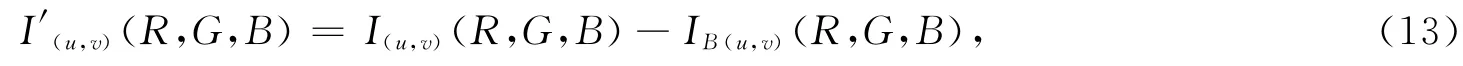
其中：I（u，v）（R，G，B）表示捕获到的图像，IB（u，v）（R，G，B）表示捕获的背景图像，（u，v）表示图像上点的坐标.

由于实际捕获的图像会产生一定的颜色失真，会对色块颜色的判断产生影响.在实验时需设置每种颜色的阈值来判断色块颜色，减少颜色失真对色块坐标提取产生的影响.设置红、绿、蓝色3种颜色的阈值分别为（Rr，Grh，Brh），（Rgh，Gg，Bgh），（Rbh，Gbh，Bb），则提取到的色块颜色判断式为下式

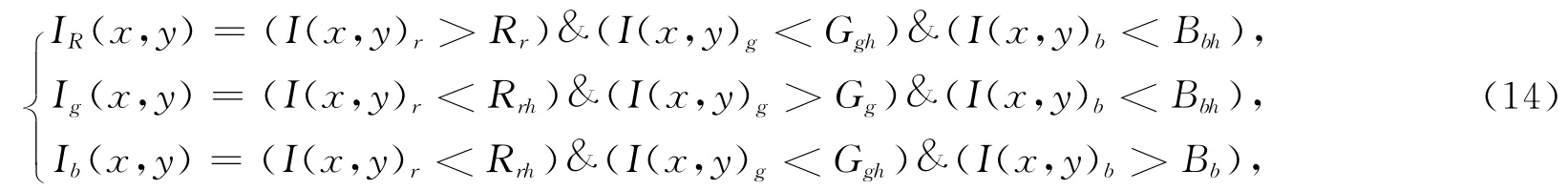
其中：I（x，y）r，I（x，y）b，I（x，y）g表示颜色块中的红、蓝、绿的颜色分量；IR（x，y），Ig（x，y），Ib（x，y）表示色块的颜色分别为红、绿、蓝.

2.3 色块中心坐标提取

实验采用色块中心作为图像的特征点，每一个色块的4个角点的横坐标和纵坐标的平均值即为色块的中心坐标.

对色块的中心坐标进行提取前，需选择要利用的摄像机图像色块区域，再对采用的色块区域进行颜色解码得到编码序列.再利用伪随机编码的特性得到投影模板上变化一致的区域，该区域即为摄像机图案选择的同一色块区域.最后分别提取选择出来的投影图像区域和摄像机图像区域中每一个色块的中心坐标，经过计算得到投影图像和摄像机图像的映射关系.

2.4 算法实现步骤

步骤1 投影仪依次投射全黑图像I1和由伪随机编码的图像I2；

步骤2 摄像机捕获分别捕获图像I′1和I′2，图像I′1为图像I′2的差分背景；

步骤3 图像I′2经过背景差分后得到I＝I′2-I′1；

步骤4 选定I图像中需要用的色块区域S，并对S中的色块解码；

步骤5 根据图像I中色块区域S解码得到的结果找寻到投影仪图像同一区域；

步骤6 提取摄像机图像I和投影仪图像选定的色块区域的色块中心坐标；

步骤7 根据图像I和投影图像提取的色块中心坐标完成单应性矩阵H求解；

步骤8 最后利用摄像机图像和投影仪图像之间的单应性矩阵H和已知的摄像机参数矩阵HC，得到投影仪参数矩阵HP，完成投影仪标定.

3　实 验

该实验由投影仪依次投射出全黑图和伪随机彩色编码图案，同时由摄像机捕获图像，将捕获的图像背景差分，色块区域选择，色块颜色判断与解码、投影图案色块阵列提取、投影图案和摄像机图案选择的区域中每个色块中心坐标提取，求取单应性矩阵等操作，利用传统的方法对摄像机进行标定得到参数矩阵，最后完成投影仪标定.

3.1 实验系统

实验系统如图4所示.使用的投影仪为NEC公司的NP-L51W＋型投影仪，它的分辨率为1 280× 800；摄像机采用MVC5001F-S00型工业摄像机，图像分辨率为2 048×1 024，2.2μm×2.2μm；投影的色块19mm×19mm.

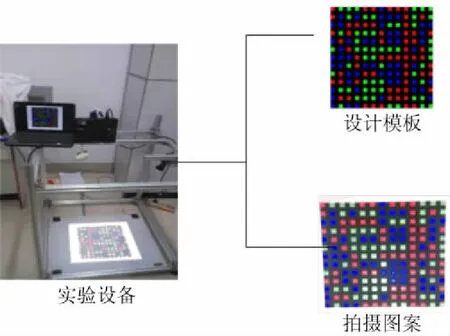
图4　实验系统Fig.4　Experimental system

3.2 实验结果

实验时，投影仪依次投射全黑图像和投影模板图像，利用摄像机捕获每一幅投影图像.对捕获的投影图片进行背景差分和色块角点检测.每个色块有4个角点，将色块4个角点的纵横坐标的平均值作为色块的中心坐标，得到投影图像和摄像机图像之间的单应性矩阵为

对摄像机采用经典的张正友平面模板法进行标定，获取摄像机的参数矩阵.最后利用式（7）的关系，得到投影仪参数矩阵如表1所示.

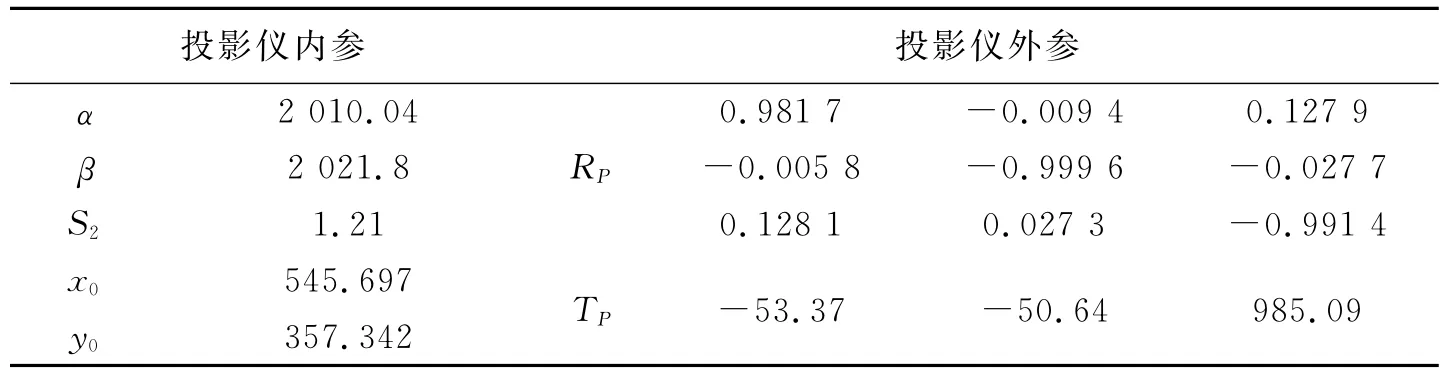
表1　论文投影仪标定方法标定结果Tab.1　Results of the proposed projector calibration method

为验证论文方法有效性，加入传统投影仪标定方法即将投影仪视为逆向的摄像机对投影仪进行标定，得到投影仪参数为表2所示.

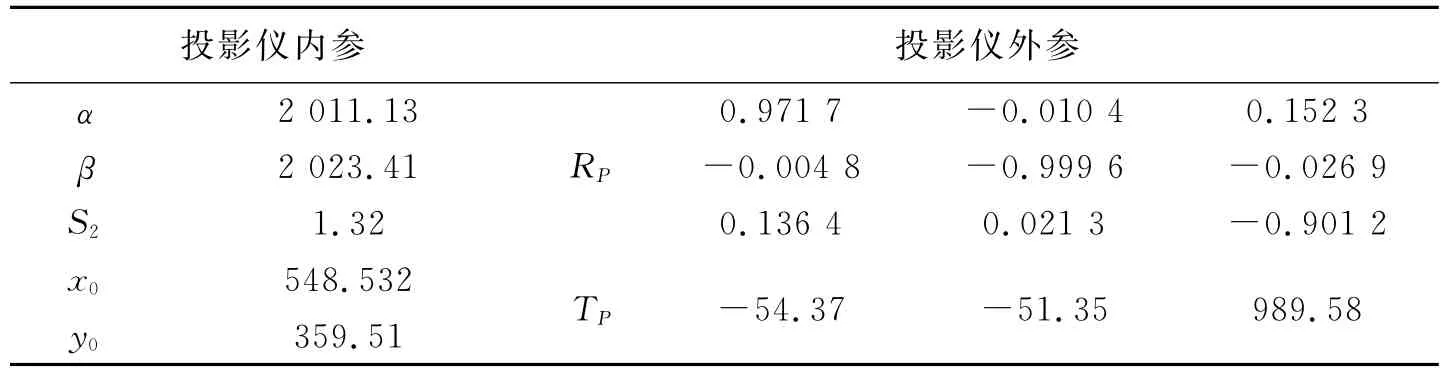
表2　传统投影仪标定结果Tab.2　Results of the traditional projector calibration method

由表1、2可知，两种投影仪标定方法都有效标定出了投影仪的内外参数，主点坐标接近图像中心，α 和β在合理范围内，为评估两种方法的精度，采用常见的反投影误差衡量进行比较，即从投影图像提取到的特征点坐标和按照投影模型得到的坐标比较得到两者间的误差，误差公式为

投影仪标定的误差如图5所示.

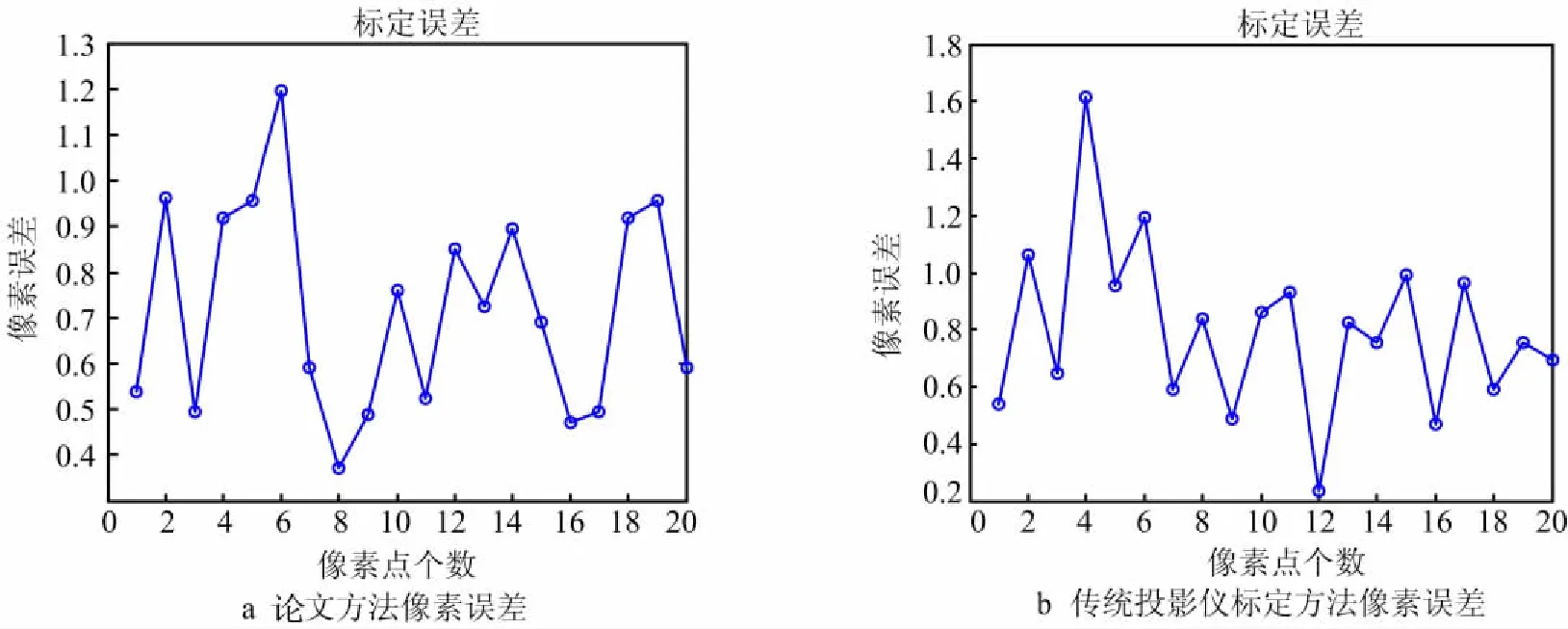
图5　投影仪标定像素误差Fig.5　Pixels error of projector calibration

实验结果表明，论文提出的方法误差在0.3和1个像素内，传统投影仪像素误差在0.5和1.2个像素内，较传统方法有较高的精度，验证了方法的有效性.

4　结束语

基于投影仪和摄像机的相对位置关系，得到投影图案和摄像机图案的确定关系，进而获得投影仪的参数矩阵.相比传统方法，该方法无需利用摄像机来得到投影特征点的坐标，且图像特征点容易被捕获，有一定实用价值.

参考文献：

［1］ GABRIEL F，HURTOS N，MASSICH J.Plane-based calibration of a projector-camera system［J］.VIBOT Master，2008，9（1）：1-12.

［2］ MORENO D，TAUBIN G.Simple，accurate，and robust projector-camera calibration［C］／／IEEE International Conference on 3DImaging Modeling Processing Visualization and Transmission，2012：464-471.

［3］ MARTYNOV I，KAMARAINEN J K，LENSU L.Projector calibration by“inverse camera calibration”［M］. Berlin：Springer Berlin Heidelberg，2011：536-544.

［4］ YAMAZAKI S，MOCHIMARU M，KANADE T.Simultaneous self-calibration of a projector and a camera using structured light［C］／／IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops，2011：60-67.

［5］ 韦争亮，钟约先，袁朝龙，等.单摄像机单投影仪三维测量系统标定技术［J］.清华大学学报（自然科学版），2009 （2）：202-205.

［6］ LIAO J，CAI L.A calibration method for uncoupling projector and camera of a structured light system［C］／／IEEE International Conference on Advanced Intelligent Mechatronics，2008：770-774.

［7］ 陈会，密保秀，高志强.基于畸变规律的三维结构光测量系统标定［J］.光学学报，2013（12）：162-170.

［8］ 傅凌进，徐海松，邹文海.一种投影仪相机系统几何配准的鲁棒算法［J］.中国图象图形学报，2010，15（11）：1664-1669.

［9］ KAZANTSEV A，PETRIU E M.Robust pseudo-random coded colored structured light technique for 3D object model recovery［C］／／IEEE International Workshop on Robotic and Sensors Environments，2008：150-155.

［10］ 廖素引，吴先良，卫敏，等.视觉测量中基于彩色伪随机编码照明模板的设计［J］.安徽大学学报（自然科学版），2011，35（1）：69-73.

（责任编辑 朱夜明）

A calibration method of projector based on the homography between the images

LI Baoshun，GU Chunxia，BAO Yaping，LI Yifeng
（College of Electronics and Information Engineering，Nanjing Tech.University，Nanjing 211816，China）

Abstract：Projector calibration is one of the key technologies in computer vision.This paper presented a calibration method of projector based on the positional relationship between the camera and projector.The method established the relation which was one to one correspondence of pixels between the image of the camera and projector image.The projector calibration was completed when getting homography between the projected image and the camera image by a series of operations to the captured image such as background subtraction，feature points extraction and so on.The method was simple and the experimental results indicated the method was practical，since the back projection error was between 0.3to 1 pixel units.

Key words：projector calibration；relative position；feature points extraction；homography；back projection error

doi：10.3969／j.issn.1000-2162.2016.01.006

作者简介：李宝顺（1974-），男，山东临沭人，南京工业大学讲师，博士.

基金项目：国家自然科学基金资助项目（11104142）

收稿日期：2015-04-16

中图分类号：TP391

文献标志码：A

文章编号：1000-2162（2016）01-0030-07