具有饱和发生率的HIV／AIDS模型的稳定性分析

王　辉，侯文涛，胡志兴，廖福成

（北京科技大学数理学院，北京 100083）



具有饱和发生率的HIV／AIDS模型的稳定性分析

王辉，侯文涛，胡志兴，廖福成

（北京科技大学数理学院，北京 100083）

摘 要：研究一类具有饱和发生率、免疫接种和时滞的HIV／AIDS模型.运用Routh-Hurwitz判据、LaSalle不变集原理、Beretta和Kuang的几何判别准则.首先，研究了系统无病平衡点的局部稳定性和全局稳定性；然后讨论了系统正平衡点的唯一存在性，并研究了正平衡点分别在系统有无时滞时稳定需要满足的充分条件；最后，对所得结果进行了数值模拟.

关键词：饱和发生率；免疫接种；稳定性

艾滋病，即获得性免疫缺陷综合症（AIDS），是由人类免疫缺陷病毒（HIV）感染引起的一种严重免疫缺陷性传染病.近年来，关于HIV／AIDS模型已经被广泛研究［1-13］.如利用自治常微分方程研究了一类包含治疗的阶段性HIV／AIDS模型［1］、具有非线性发生率的HIV／AIDS模型［3］、一类具有脉冲接种的HIV／AIDS模型［3］、一类具有时滞和免疫接种的阶段性HIV／AIDS模型［8］等.笔者根据相关文献建立的数学模型［8］，考虑饱和发生率，建立了一个具有时滞和免疫接种的阶段性HIV／AIDS模型，并研究了模型的平衡点的稳定性.

1　模型的建立

下面研究一类具有饱和发生率和免疫接种的HIV／AIDS时滞模型

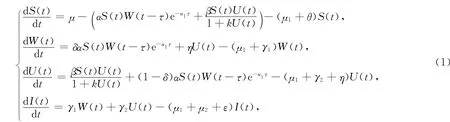
其中：α和β表示有效接触率，其他参数代表的含义均参照文献［8］.

系统（1）的初始条件为

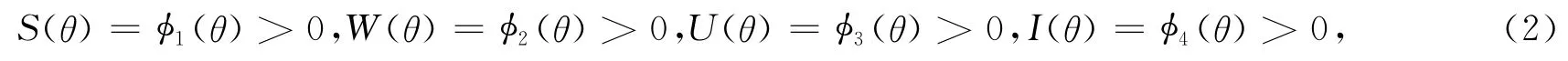
2　平衡点及其稳定性分析

2.1 无病平衡点稳定性分析

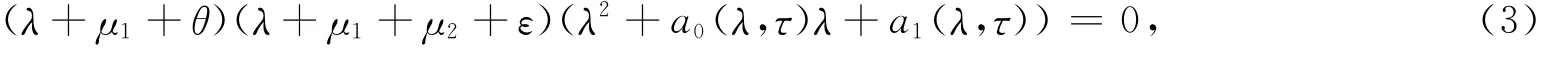
其中

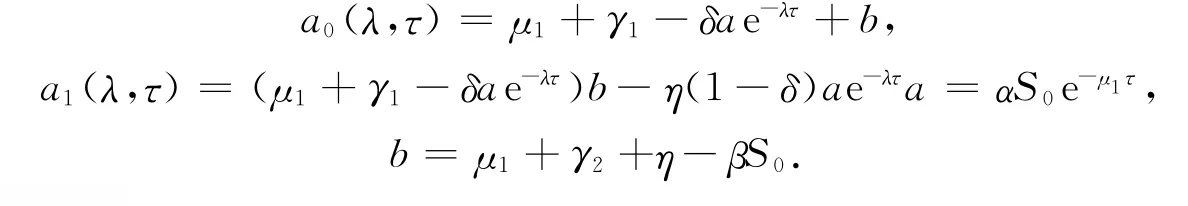
定义基本再生数为

定理1 若R0＜1，则无病平衡点E0对所有的τ≥0是局部渐近稳定的.

证明 显然（3）有两个负根λ1＝-（μ1＋θ），λ2＝-（μ1＋μ2＋ε）.因此无病平衡点E0的稳定性由方程λ2＋a0（λ，τ）λ＋a1（λ，τ）＝0根的情况决定.

首先，当τ＝0时，方程f（λ，τ）＝0变为

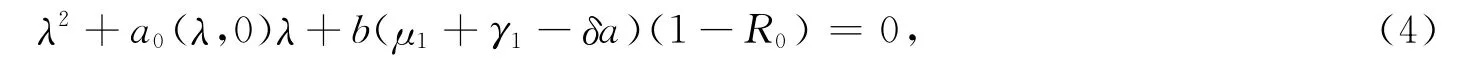
计算可得，当R0＜1时，方程（4）所有系数都为正，且有两个负实部的根.从而平衡点E0在τ＝0时是局部渐近稳定的.

其次，若λ＝iω（ω＞0）是方程f（λ，τ）＝0的纯虚根，分离实部和虚部并且再平方相加得

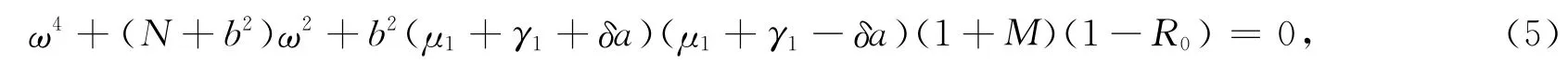
由R0＜1时μ1＋γ1-δa＞0，从而方程（5）中系数都为正.因此方程（5）没有正根.

综合上述可得，若R0＜1，平衡点E0对所有的τ≥0是局部渐近稳定的.

2.2 染病平衡点稳定性分析

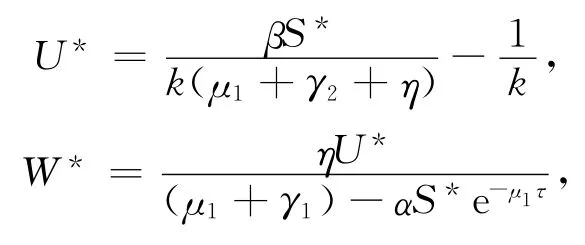
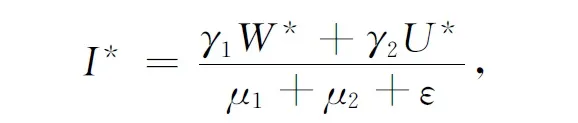
而S＊满足方程.由关于S＊的表达式知，且

定义

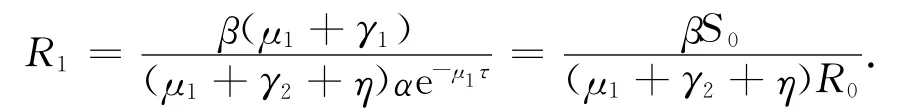
定理2系统存在唯一的染病平衡点E＊＝（S＊，W＊，U＊，I＊）T，并且此时系统满足，1＜R0＜

证明 由W＊，U＊，I＊都是正值可解得

显然R1≤1时，系统不存在正平衡点.因此设R1＞1，若Δ＜0系统显然没有正平衡点；若Δ＞0，则有两个正根设为，.其中

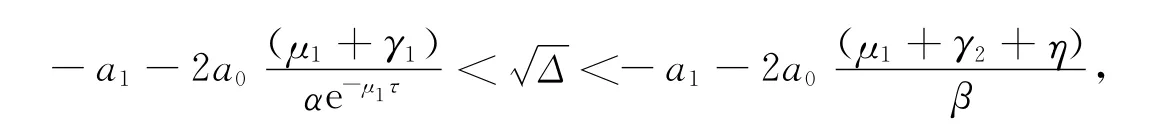
将a0，a1，a2的表达式代入上式计算可证得上式成立.

综合上述，定理2得证.

下面考虑若正平衡点存在时，正平衡点的稳定性.令

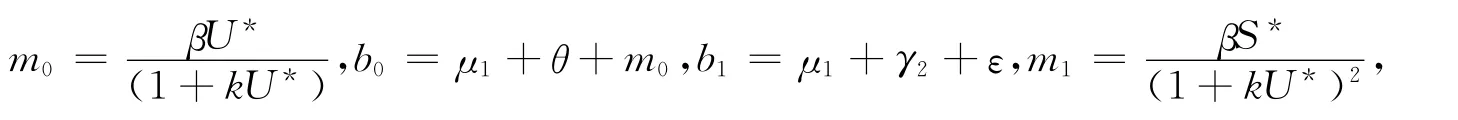
则系统在正平衡点E＊＝（S＊，W＊，U＊，I＊）T处特征方程为

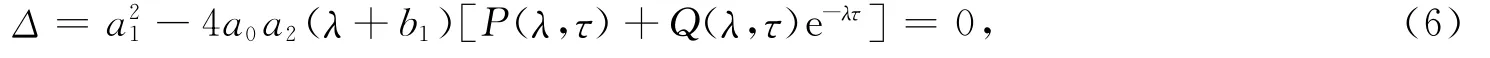
其中

显然特征方程有一根λ＝-b1，因此正平衡点的稳定性由以下方程根的情况决定

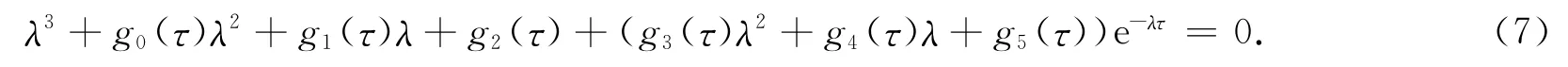
定理3 如果1＜R0＜min｛βS0／（μ1＋γ2＋η），m1μS0／（μ1＋γ1）ηS＊2｝，则当τ＝0时平衡点E＊是局部渐近稳定的.

证明 当τ＝0时，特征方程变为

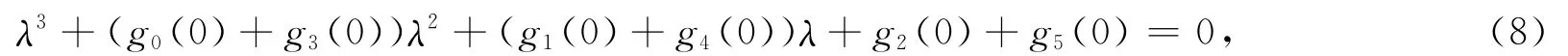
其中：Δ1＝g0（0）＋g3（0），Δ2＝（g0（0）＋g3（0））（g1（0）＋g4（0））-（g2（0）＋g5（0）），Δ3＝（g2（0）＋g5（0））·Δ2.

如果1＜R0＜min｛βS0／（μ1＋γ2＋η），m1μS0／（μ1＋γ1）ηS＊2｝，计算可得Δ1＞0，Δ2＞0和Δ3＞0.由Routh-hurwitz判据知，当τ＝0时平衡点E＊是局部渐近稳定的.

下面探讨方程（7）纯虚根λ＝iω（ω＞0）的存在性.设λ＝iω（ω＞0）是特征方程的一纯虚根，代入特征方程分离实部和虚部可解得

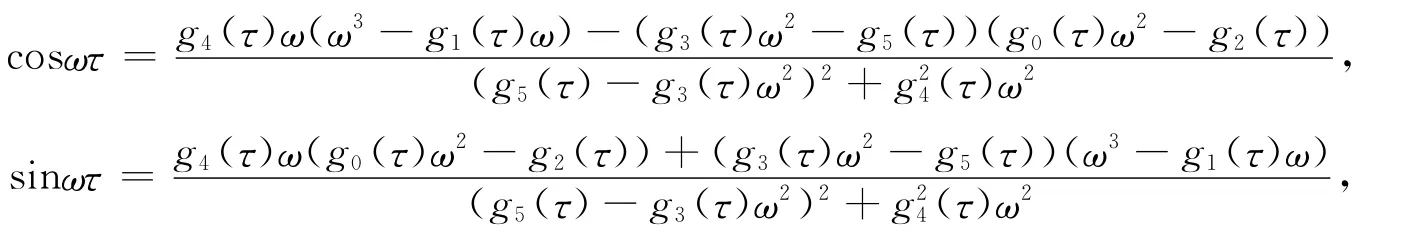
将上面两式两边分别平方，整理相加得

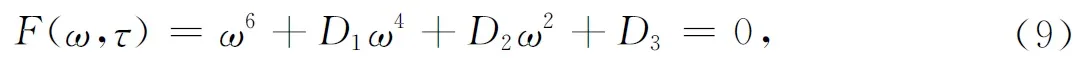
其中

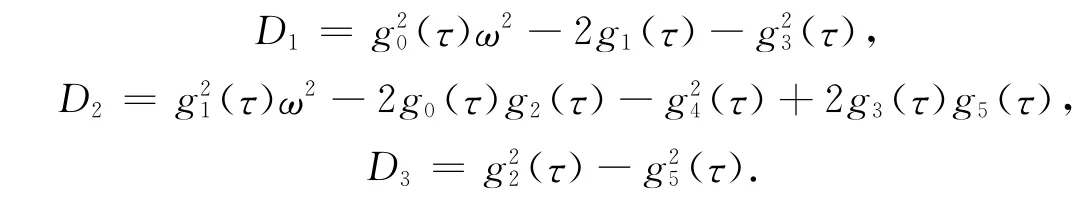
令x＝ω2，则上式变为

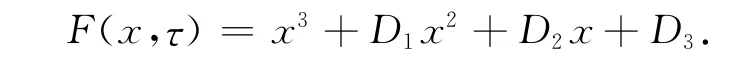
易得

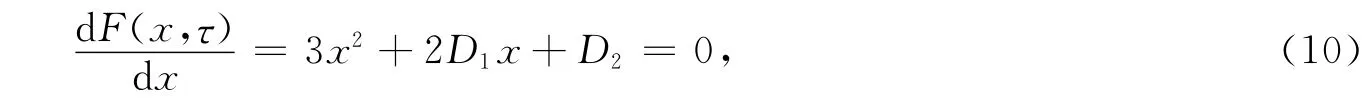
定理4 如果1＜R0＜min｛βS0／（μ1＋γ2＋η），m1μS0／（μ1＋γ1）ηS＊2｝成立，则染病平衡点E＊对所有τ≥0是局部渐近稳定的，如果下列条件之一满足

（1）D3≥0且M≤0

定理5 如果1＜R0＜min｛βS0／（μ1＋γ2＋η），m1μS0／（μ1＋γ1）ηS＊2｝成立，则F（x，τ）＝0至少有一个正根，如果下列条件之一满足（1）D3＜0；（2）D3≥0且

利用文献［10］建立的几何判别准则.不失一般性，设ω（τ）是其任意一个正根.构造集合I＝｛ττ≥0，F（ω，τ）＝0｝有正解，即当τ∈I 的时候，F（ω，τ）＝0有正解ω（τ）；而当τ∈I 的时候，F（ω，τ）＝0没有正解.

对τ∈I，定义一个角θ（τ）∈［0，2π）满足cosωτ和sinωτ表达式.则θ（τ）与ω（τ）τ必须满足如下关系

根据Beretta和Kuang［10］可知：Sn（τ）在I上连续可微，且横截条件为

定理6 假设ω（τ）是F（ω，τ）＝0的定义在I上的连续可微的正解，且对某个n∈N0，在某τ＊∈I 处有Sn（τ＊）＝0，则在当τ＝τ＊时，系统特征方程有一对纯虚根λ＝±ω（τ＊），且如果横截条件δ（τ＊）＞0（＜0），那么随着τ的增加并越过τ＊时，这对纯虚根所对应的根将会从左（右）半平面穿过虚轴进入右（左）半平面.

3　结束语

作者考虑了更接近实际的具有饱和发生率和免疫接种的HIV／AIDS时滞动力学模型.分析得出了模型的基本再生数R0，R0＜1时，无病平衡点是局部渐近稳定的.时，唯一的染病平衡点存在，并且得出了染病平衡点稳定性的充分条件.因此，在实际的疾病预防控制工作中，应该考虑加大HIV／AIDS疫苗接种量，重视利用抗逆转录病毒治疗，控制基本再生数R0在小于1的范围内，从而控制疾病的扩散.可见论文的结论对疾病的预防和控制有理论和实际的指导意义.

参考文献：

［1］ CAI L，LI X，GHOSH M，et al.Stability analysis of an HIV／AIDS epidemic model with treatment［J］. Comput Appl Math，2009，229（1）：313-323.

［2］ MUKANDAVIRE Z，GARIRA W，CHIYAKA C.Asymptotic properties of an HIV／AIDS model with a time delay［J］.Math Anal Appl，2007，330（2）：916-933.

［3］ NARESH R，TRIPATHI A，SHARMA D.A nonlinear AIDS epidemic model with screening and time delay ［J］.Appl Math Comput，2011，217（9）：4416-4426.

［4］ GAO S，CHEN L，NIETO J J.Analysis of a delayed epidemic model with pulse vaccination and saturation incidence［J］.Lancet，2006，24（35）：6037-6045.

［5］ 崔倩倩，张强.一类具有饱和发生率的SIRS传染病模型的全局性分析［J］.四川理工学院学报（自然科学版），2012，25：1173-1549.

［6］ 内藤敏机，原惟行.时滞微分方程-泛函微分方程引论［M］.北京：科学出版社，2002.

［7］ 肖燕妮，周义仓，唐三一.生物数学原理［M］.西安：西安交通大学出版社，2012.

［8］ LIU D D，WANG B.A novel time delay HIV／AIDS model with vaccination ＆antiretroviral therapy and its stability analysis［J］.Applied Mathematical Modelling，2013，37：4608-4625.

［9］ KAJITA E，OKANO J T，BODINE E N，et al.Modelling an outbreak of an emerging pathog-en［J］.Nat Rev Microbiol，2007，5（9）：700-709.

［10］ BERETTA E，KUANG Y.Geometric stability switch criteria in delay differential systems with delay dependent parameters［J］.SIAM J Math Anal，2002，33：1144-1165.

［11］ XU R，MA Z E，WANG Z P.Global stability of a delayed SIRS epidemic model with saturation incidence and temporary immunity［J］.Computers and Mathematics with Applications，2010，59：3211-3221.

［12］ BUNNELL R，OPIO A，MUSINGUZI J，et al.HIV transmission risk behavior among HIV-infected adults in Uganda：results of a nationally representative survey［J］.AIDS，2008，22（5）：617-624.

［13］ VIVIANA S，DAVID D H.HIV-1dynamics in vivo：implications for therapy［J］.Nature Microbiol，2003 （1）：181-190.

（责任编辑 朱夜明）

Stability analysis of the HIV／AIDS model with saturated incidence rate

WANG Hui，HOU Wentao，HU Zhixing，LIAO Fucheng
（College of Mathematics and Physics，Beijing University of Science and Technology，Beijing 100083，China）

Abstract：In this paper，an HIV／AIDS model with saturation incidence，immu-nization and time delay was considered.By using Routh-Hurwitz criterion，LaSalle invariant set principle，Beretta and Kuang geometric criterion，firstly，the local stability and global stability of the disease-free equilibrium point were studied.Then，the existence and uniqueness of the positive equilibrium point was discussed and the sufficient condition for the stability of the positive equilibrium point was researched whether the time delay was in the system or not.Finally，the results obtained by numerical simulation.

Key words：saturated incidence；immunization；stability

doi：10.3969／j.issn.1000-2162.2016.01.004

作者简介：王 辉（1965-），女，山西榆次人，北京科技大学副教授，硕士生导师.

基金项目：国家自然科学基金资助项目（61174209）；北京科技大学冶金工程研究院基础研究基金资助项目（YJ 2012-001）

收稿日期：2015-03-15

中图分类号：O175

文献标志码：A

文章编号：1000-2162（2016）01-0018-05