基于热工及工艺参数的回转窑测温模型应用

邱立运，姚谦礼

（1.湘潭大学信息工程学院，湖南湘潭411105；2.中冶长天国际工程有限责任公司，湖南长沙410007；3.国家烧结球团装备系统工程技术研究中心，湖南长沙410007）

基于热工及工艺参数的回转窑测温模型应用

邱立运1，2，3，姚谦礼1

（1.湘潭大学信息工程学院，湖南湘潭411105；2.中冶长天国际工程有限责任公司，湖南长沙410007；3.国家烧结球团装备系统工程技术研究中心，湖南长沙410007）

工业生产过程中，回转窑的温度直接影响物料的煅烧质量，选择准确、实用的回转窑实时在线测温方法对保证回转窑正常生产有着重要意义。本文提出一种基于热工及工艺参数的回转窑测温数学建模方法，获得窑内温度。并通过在工业现场的大量实验，验证了模型的正确性及可行性。

回转窑；软测量；工艺参数；数学模型

回转窑窑内温度的检测一直被认为是一个难题，现有的各类回转窑窑内温度检测装置，多数存在使用寿命短、价格昂贵、测温点数量有限、测温滞后性大等问题，难以保证稳定、可靠地工作，也很难应用于大型回转窑[1]。因此选择准确、经济、实用的回转窑在线测温方法是保证回转窑正常工作的重要手段之一。

数学建模的测温方法是一种软测量方法，软测量是用易测过程变量与难直接测得的待测过程变量之间的数学关系，通过数学计算和估计，最终获取待测过程变量，广泛应用于各测量领域。现有的数学建模方法有基于过程相似性的模型迁移法[2]、数据驱动建模方法[3-6]、铁矿氧化球团回转窑三维温度场仿真模型[7]等。

回转窑测温的数学建模方法有很多，但从相关的资料看，多数方法基本限于理论、仿真研究阶段。本文介绍的基于热工及工艺参数的回转窑测温数学建模方法，有着简单、可靠、易用的一次检测元件，结合生产工艺参数建立的数学模型，易于操作及通过计算机实现。不仅限于理论研究，在工业现场的实验中也取得了较好的效果。

1 基于热工及工艺参数的回转窑测温数学建模方法

本文用在回转窑表面安装不穿透耐火炉衬的热电偶的方法，测量回转窑耐火炉衬的某一截面处温度、窑表面温度、环境温度等参数，结合实际工艺生产参数，建立回转窑测温的热工数学模型，最终得到回转窑对应炉衬截面处测温位置的内壁温度、回转窑内烟气温度等，从而指导回转窑生产操作。

1.1 一次测温元件及温度信号采集系统结构

回转窑测温的数学建模是否成功与一次测温元件的安装有重要关系。根据工艺及热工要求，从窑壳向内开设Φ3～6温度测量孔，该孔不穿透炉衬耐火材料层，保留100～150 mm。在热电偶安装时，为能更真实地反应窑内温度，要尽可能地缩小测温孔内端部至窑内壁的厚度，以提高耐火材料导热反应速度。

利用普通热电偶检测得到的测温孔内端部温度以及表面热电偶检测到的预留孔附近窑身外壁温度，结合热工计算模型的方法得到回转窑内壁温度。

图1是温度信号采集系统的硬件结构示意图，系统中的信号处理单元由转动信号处理单元和固定接收信号处理单元组成。其中转动信号处理单元采集热电偶和热电阻的信号，通过冷端补偿和线性化处理，得到热电偶的热端温度，然后通过无线通信方式，把热电偶温度信号、电池电压信号、温差发电电压信号和热电偶的状态信号发送给窑附近的固定接收信号处理单元。固定接收信号处理单元接收到转动信号处理单元发送过来的数据，通过Profibus-DP总线把数据发送给主计算机系统。

图1 硬件系统结构示意图

1.2 测温模型建立的基本原理

回转窑作为高温焙烧设备，不可避免地涉及到传热，其传热形式是多样化的。当回转窑结圈（厚度0～δ1m，厚度为0时表示回转窑未结圈）时，回转窑内壁与结圈物料之间主要发生热传导，高温气体与结圈物进行热对流、热辐射，耐火材料与回转窑外表面之间产生热传导，回转窑外表面与空气发生热对流和热辐射。假定回转窑在某一横截面上由五层组成，如图2所示，每层的物质具有各向同性，温度传递从左到右由高向低。在此基础上，建立回转窑测温数学模型。

图2 回转窑内外各物质组成及温度示意图

1.3 测温模型的研究

1.3.1 对流换热系数h的确定

在无限空间中自然对流换热准则方程式可由努赛尔（Nusselt）准则给出，方程式如下：

式中：Num是由平均表面传热系数组成的Nu数；Nu为努赛尔数，表征对流换热强度的准则；Gr为格拉霍夫（Grashof）数；Pr为普朗特（Prandtl）数；C、n根据换热表面的形状与位置、热边界条件以及层流或湍流的不同流态取值，常数；λ为流体导热系数[8]。

式中：g表示重力加速度，取g=9.802 8m/s2；av是流体膨胀系数，对于空气，av=1/T；T为流体的定性温度；ΔT为接触壁面同流体的温差，℃；l为特征尺寸（此处为回转窑外径），m；v表示运动黏性系数，m2/s。

1.3.2 热流密度q的确定

热流密度q是单位时间内通过物体单位横截面积的热量，热流密度在回转窑测温模型中是不可缺少的量。热流密度q的计算方法如下：式中：h1和h2分别表示对流换热系数和辐射换热系数，W/（m2·℃）；Tb为窑表面温度，℃；T∞为环境温度，℃，这两个值均由温度检测元件检测得到；λ表示定性温度下空气导热系数，在53～200℃温度区间内适用，W/（m2·℃）；σ为波尔兹曼常数，5.67×10-8；ε为窑表面的发射率，对于氧化的钢取0.8。

1.3.3 回转窑燃烧产物温度（气氛温度）的计算

根据工况时进入回转窑的各类燃料、空气流量、物料量等计算窑内气氛温度T0，当出现结圈或炉衬剥落时，炉衬无变化时的计算模型不再适用，此时可利用工况时得到T0修正测温模型，并可计算得到结圈物厚度热工计算模型的值，即结圈物厚度。按照窑内物料的化学反应可分为氧化性回转窑和还原性回转窑两种类型来计算燃烧产物温度。本文以还原性回转窑为例，说明回转窑燃烧产物温度的计算方法，氧化性回转窑燃烧产物计算方法与之类似不再赘述。还原性回转窑区域划分如图3所示。

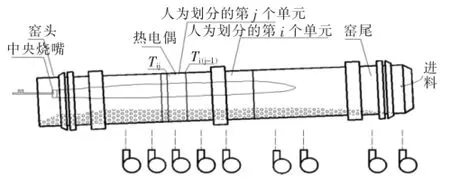
图3 还原性回转窑区域划分示意图

直接还原回转窑第i单元第j段中燃烧后烟气产物温度计算公式如下：式中：ti0为第i单元内燃烧产物的实际计算平均温度，℃；

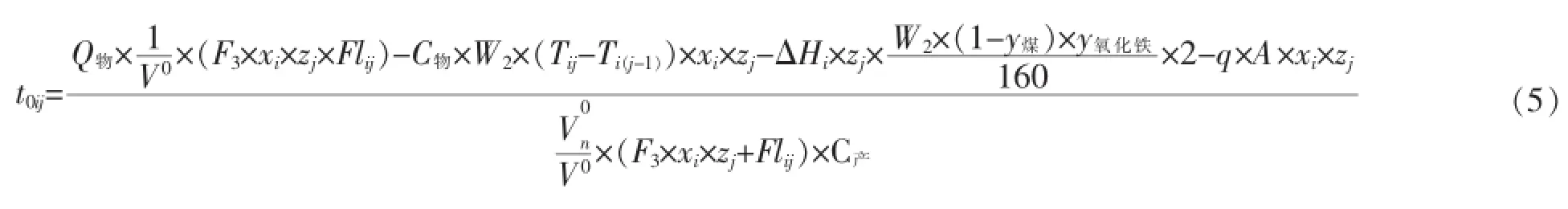
W1为每小时煤的入窑量，kg/h，通过配料秤检测数据得来；

W2为每小时物料的入窑量，kg/h，通过链篦机前物料量数据软测量得来；

C物为入窑物料的比热，kJ/(kg·℃)，通过化验得到；

q为热流密度，W/m2，通过软测量计算得到；

A为窑的总表面积，m2；

C产为烟气定压平均比热，常数，kJ/（m3·℃），查表可得；

tij产为第i单元第j段内燃烧产物的实际计算平均温度，℃；

Ni为第i个分区内二次烧嘴的数量；

V0表示每千克煤粉完全燃烧需要的理论空气量，m3/kg；

V0n表示每千克煤粉完全燃烧所产生的理论烟气量，m3/kg；

xi为各步还原反应所占据的窑长百分比，工况稳定时基本为常量；

zj为第i个分区内按二次风烧嘴划分的第j段占第i分区的百分比，工况稳定时基本为常量；

y煤表示入窑物料中煤粉的质量百分比，基本为常量；

y氧化铁表示入窑物料中混入煤粉之前物料中Fe2O3的含量百分比，基本为常量；

Ti（j-1）为第i单元第j段入口物料温度，℃，同一工况下基本为常量；

Tij为第i单元第j段出口物料温度，℃，同一工况下基本为常量；

ΔHi表示第i步还原反应中1 mol球团矿吸收的热量，J/mol，查表可得；

F1ij为第i分区第j段由二次风烧嘴补充进入窑内的助燃空气量，m3/h，可由检测手段获得。

1.4 窑内温度检测与炉衬厚度变化数学模型

在确定对流换热系数h和热流密度q后，可将炉衬分为无变化、有结圈物和剥落三种情况建立回转窑窑内温度检测的数学模型。

（1）无变化时

当回转窑无结圈时如图4所示，已知耐火材料层厚度为δ2，单位m。由热电偶测温点温度和该点热流密度可以建立回转窑内表面测温数学模型：

式中：T1表示回转窑内表面温度，℃；T3表示热电偶测温点温度，℃；q为热电偶测温点处的热流密度，W/m2；δ2表示耐火材料层厚度；λ2表示耐火材料层导热系数，W/（m·℃），可通过化验得到。

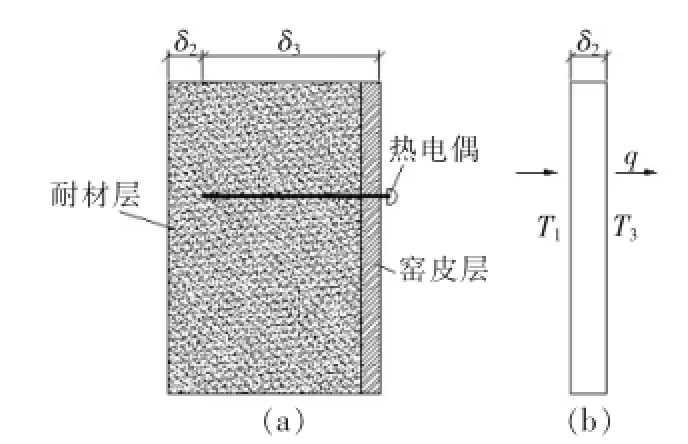
图4 回转窑内表面测温模型（无变化）示意图

根据炉衬无变化时的回转窑内表面温度T1和对应检测点处的气氛温度T0，建立窑内气氛温度与窑内壁温度的对应关系T1=βT0+b，得到β与b的值。当炉衬出现结圈或剥落时，用于修正测温数学模型。

（2）有结圈物

在回转窑内有结圈物时，如果继续使用炉衬无变化时的测温模型会导致测量结果不准确。故使用上述温度修正数学模型获取回转窑内表面温度，并可由此推算出结圈物厚度。设结圈厚度为δ1，单位m，成分稳定，如图5所示。

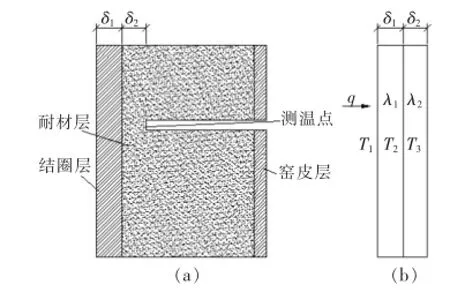
图5 回转窑内表面测温模型（结圈时）示意图

结圈厚度计算的数学模型为：

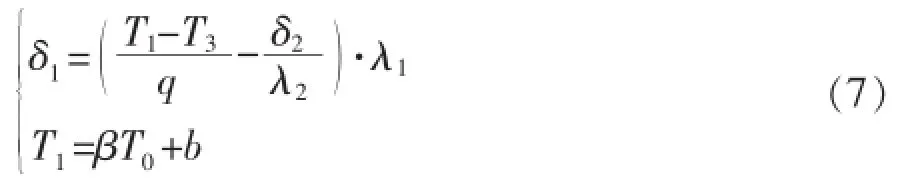
式中：λ1为结圈层导热系数，W/（m·℃）；β、b为常数。其它参数的意义同式（5）。

（3）炉衬剥落

与结圈时同理，炉衬剥落时原测温数学模型不再准确，故由温度修正数学模型计算回转窑内表面温度T1，并计算出剥落物厚度δ′1，单位m。如图6所示。

剥落物厚度计算的数学模型为：

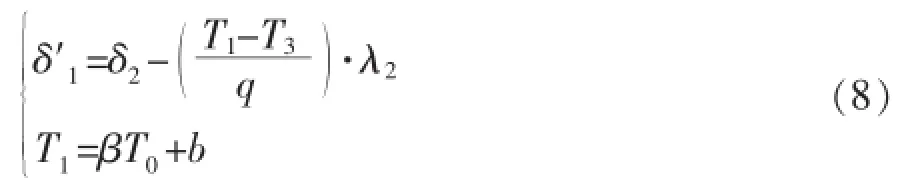
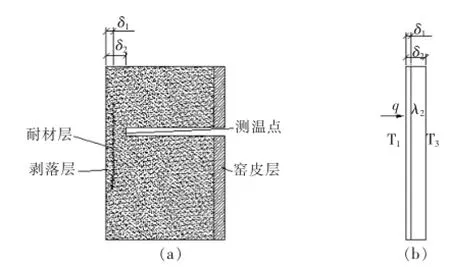
图6 回转窑内表面测温模型（剥落时）示意图

2 测温数学模型准确性验证

（1）采集测温信号

回转窑测温信号采集模块的原理图如图7所示，AD转换器6通道、低功耗、内置仪用运放的16位ADC芯片AD7795，一共4片AD7795，其中2片AD7795采集12路热电偶信号，剩下2片AD7795，用于采集2路热电阻PT100信号和8路热电偶信号。考虑到供电方式为电池供电，故选用低功耗的微控制器MSP430F2618，该芯片有多种低功耗模式，并且在1MHZ主频下，工作电流只有220 uA。参数存储芯片选用93C46，看门狗芯片选择SP706RE，复位电压2.63 V。无线通信模块采用LSD4RF-21717M41，该模块发射功率达到16 dBm，接收灵敏度达到-115 dBm，且通过端口配置，让其工作在低功耗模式下。将采集到的温度信号传输到上位机软件中计算并储存，用于验证模型的准确性。

图7 测温信号采集模块原理图

（2）实验数据分析

以湖南某钢厂的氧化球团回转窑作为实验对象，获取的实验数据如表1所示。

从表1可以看出，热流密度的计算值比较平稳，基本只与试验装置外表面温度相关，且成单调递增函数关系，说明了热流密度模型的正确性、可行性。

表1 实测数据与分析计算数据

通过测温数学模型计算的回转窑内表面温度与对应位置实际检测的温度基本比较平稳，差值率-3.1%～7.4%，在允许范围内，说明了基于热工及工艺参数的回转窑测温数学模型的准确性及可行性。

3 结语

本文提出了一种基于热工及工艺参数的回转窑测温数学模型，并将该测温方法应用于湖南某钢厂的回转窑，通过大量的实验，验证了热流密度模型与测温模型的准确性与可行性，测温误差在允许的误差范围内。本文建立的数学模型可在各类不同规模不同类型的回转窑上使用，回转窑或工艺类型不同时，对热工模型稍作改动即可。

[1]邱立运,姚谦礼.回转窑测温技术现状综述及发展趋势预测[J].工业炉,2014（6）∶16-20.

[2]张立,高宪文,王介生，等.基于模型迁移方法的回转窑煅烧带温度测量[J].东北大学学报,2011,32(2)：175-178.

[3]郜传厚,渐令.复杂高炉炼铁过程的数据驱动建模及预测算法[J].自动化学报,2009,35(6)：725-729.

[4]CAIY.Research on softmeasurementmodeling for industry rotary kiln based on flexible neural network[C]//2012 International Conference on Computer Science and Electronics Engineering. Hangzhou∶IEEE Computer Society,2012.

[5]VAPNIK V N.The Nature of Statistical Learning Theory[M].New York∶Springer-Verlag,2000.

[6]袁平,毛志忠,王福利.基于多支持向量机的软测量模型[J].系统仿真学报,2006,18(6)∶1458-1465.

[7]范晓慧，李俊,陈许玲，等.铁矿氧化球团三维温度场仿真模型[J].中南大学学报,2012，43(8)：2896-2899.

[8]杨世铭,陶文铨.传热学[M].4版.北京：高等教育出版社,2006.

Application of Tem perature M easurement M odel for Rotary Kiln Based on Therm al and Process Param eters

QIU Liyun1,2,3,YAOQianli1
（1.College of Information Engineering,Xiangtan University,Xiangtan 411105,China; 2.Zhongye Changtian International Engineering Co.,Ltd,Changsha 410007,China;3.National Engineering Research Center of Sintering and Pelletizing Equipment System,Changsha 410007,China)

The temperature of rotary kiln will influence the quality of product in the industrial production.So,accurate and real-time temperature of rotary kiln is important to ensure the normal production.A kind ofmathematicalmodel that can gain the rotary kiln temperature and based on thermal and process parameters is presented.Finally,a large of experiments verified the correctness and feasibility of themodel.

rotary kiln;softmeasurement;polytechnic parameters;mathematicalmodel

TH 811

A

1001-6988（2016）05-0053-05

2016-06-23

邱立运（1976—），男，高级工程师，长期从事冶金自动化与检测系统设计及研究工作.