列车脱轨撞击下盾构隧道管片衬砌开裂与接头螺栓动力响应特性研究

晏启祥，李彬嘉，李　彬，徐亚军，耿　萍

(1.西南交通大学 交通隧道工程教育部重点实验室，四川 成都　610031；2.西南交通大学 土木工程学院，四川 成都　610031；3.铁道第三勘察设计院集团有限公司，天津　300000)

盾构隧道为装配式管片衬砌结构，管片主要靠螺栓等接头构件连接，一旦隧道内发生列车脱轨撞击隧道事故，在列车撞击荷载的作用下，盾构隧道管片衬砌会出现损伤和开裂，并可能出现螺栓断裂失效、接缝板破坏、衬砌环垮塌等重大安全事故。有鉴于此，为了掌握盾构隧道在列车撞击荷载作用下的破坏机理，给盾构隧道设计工作者提供防撞设计理论依据，保证盾构隧道的运营安全，急需对列车撞击荷载作用下盾构隧道管片衬砌的开裂破坏过程以及接头螺栓的动力响应特性进行研究。

目前，国内外针对列车脱轨撞击问题研究的主要目的是为列车的耐撞性和吸能设计提供依据。JEONG-Seo Koo等[1]对韩国高速列车开展了列车耐撞性优化设计；房加志等[2]利用有限元法研究了高速列车铝合金材料的耐撞性；David Tyrell等[3]模拟了列车与列车的撞击实验，对列车吸能部件的效能进行了测试；姚松等[4]研究了薄壁结构车辆吸能部件的碰撞特性，为列车的吸能设计提供参考。对于列车撞击荷载作用下被撞结构方面，向俊等[5]通过对高速铁路在无砟轨道桥梁上脱轨的全过程进行数值模拟，开展了防撞结构设计；晏启祥等[6-9]通过建立三维列车撞击有限元模型，获得了不同列车编组、不同撞击速度和撞击角度下列车的近似撞击力荷载时程曲线，分别研究了列车撞击力最大值和撞击时间与列车撞击速度及角度的关系；并对200 km·h-1速度下列车脱轨斜向撞击隧道时，盾构隧道二次衬砌对管片衬砌的防护效果进行了分析。本文在已有列车撞击荷载时程曲线的基础上，着重对盾构隧道的拼装式管片衬砌开裂行为以及接头螺栓的动力响应特性进行研究。

对于管片衬砌开裂这类非线性问题常采用扩展有限元法模拟。自美国西北大学Belytschko[10]于1999年提出求解非连续问题的扩展有限元法以来，其在混凝土开裂模拟方面就得到了广泛应用，如Wells[11]，Mo⊇s[12]和方修君等[13]将黏聚裂纹模型嵌入到扩展有限元法当中对混凝土构件的非线性开裂进行模拟，验证了扩展有限元法在模拟混凝土静态开裂方面的可靠性；J.Réthoré等[14]，Goangseup ZI等[15]采用扩展有限元法模拟了动态裂纹的扩展过程，显示了扩展有限元法在模拟冲击等动态荷载作用下裂纹扩展的可行性。

因此，本文采用扩展有限元法模拟盾构隧道在列车撞击荷载作用下管片衬砌裂缝的分布和扩展过程，分析接头螺栓的动力响应特性，为盾构隧道管片衬砌的防撞安全提供理论依据。

1　衬砌开裂模拟的扩展有限元理论

扩展有限元法是在传统有限元框架下提出的一种用于解决间断问题的方法，如裂纹、孔洞、夹杂等间断问题，它不依靠网格重划分，而是通过在传统有限元中引入非连续的位移模式解决间断问题，其优势是避免了传统有限元法对计算网格的依赖，显著地提高了计算效率[16]。

扩展有限元法最重要的环节就是要构造1个近似函数。其近似函数的构造一般基于单位分解法，其基本思想是任意函数都可以用域内的1组局部函数来表示。扩展有限元法利用形函数构造求解域上的1组单位分解函数，从而在计算区域内位移u(x)的近似解可表述为

(1)

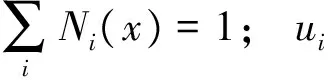
当计算区域内出现裂缝时，位移近似解uh(x)可进一步表示为[17]

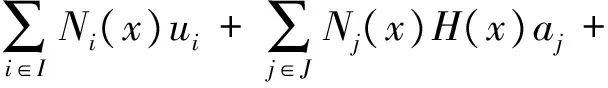
(2)

2　衬砌开裂分析模型

以某水下盾构隧道为研究对象建立盾构隧道管片衬砌非线性开裂三维有限元模型。该隧道围岩主要为砂性土、风化泥质粉砂。隧道管片衬砌内半径为4.67 m，外半径为5.15 m，厚度为0.48 m，幅宽为2.0 m。衬砌环由5块标准块B1—B5(49.09°)、2块邻接块L1—L2(49.09°)和1块封顶块F(16.36°)构成。

盾构隧道管片衬砌开裂分析采用通用有限元软件Abaqus进行。模型的长×宽×高为90 m×60 m×60 m，模型边界采用黏弹性人工边界，用连续分布的并联弹簧—阻尼器系统模拟。为减小工作量并提高计算效率，只对撞击目标环(同时也是研究目标环)以及其前、后2环共3环管片进行通缝拼装式近似建模，对于其他管片环，则基于纵向抗弯刚度等效原则，通过弱化接缝位置混凝土弹性模量的方式近似模拟。由此建立的盾构隧道管片衬砌非线性开裂三维有限元模型如图1所示。

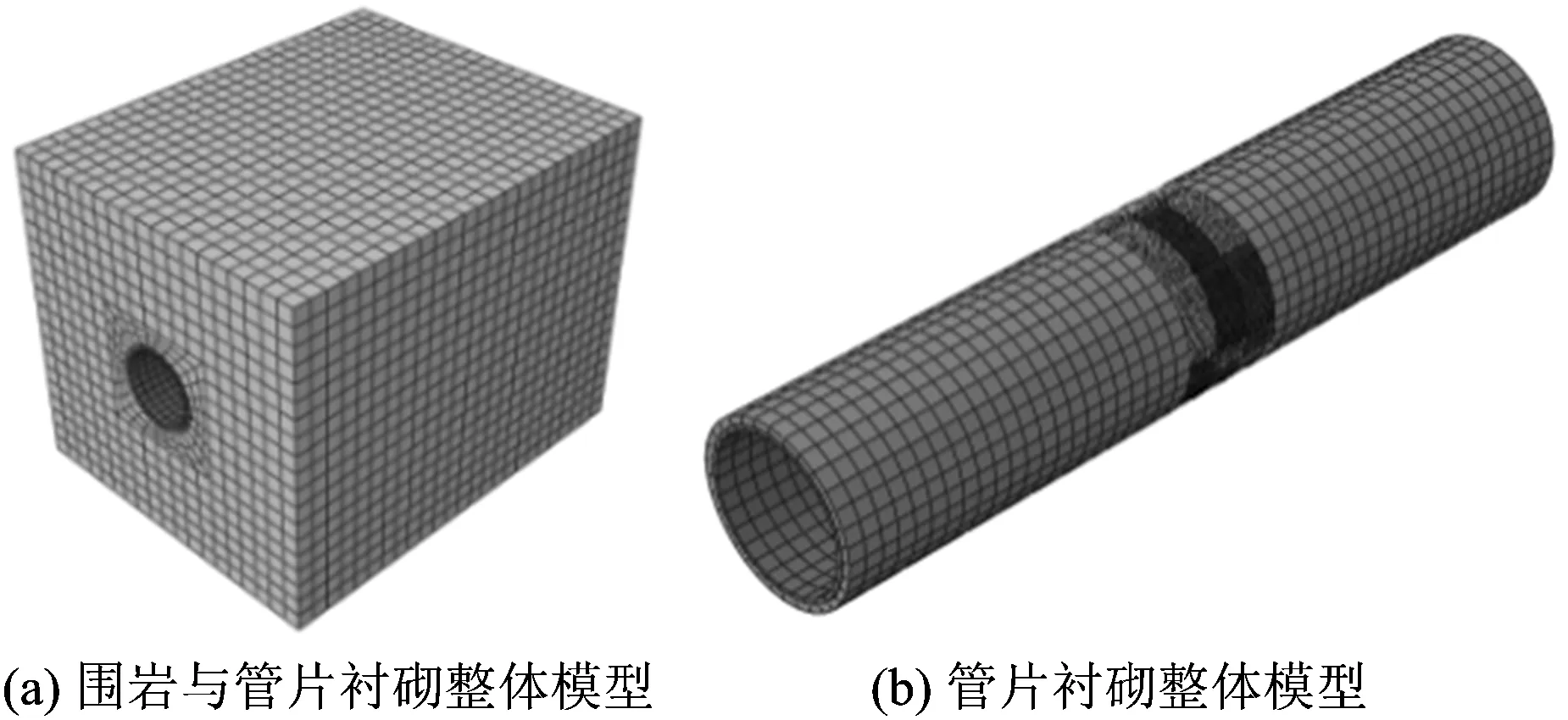
图1　盾构隧道管片衬砌非线性开裂三维有限元模型

图2为3环通缝拼装式管片接触模型的局部示意。管片与管片之间，前后相邻管片衬砌环与目标环之间采用接触面模拟，其中法向为硬接触，切向为库伦摩擦接触，摩擦系数取0.6。接头螺栓嵌入到相邻管片中。而3环管片以及前后衬砌段与围岩之间也采用接触面模拟，但其法向采用惩罚刚度法，切向仍为库伦摩擦接触，摩擦系数取0.8。3环管片与其前后衬砌段的连接采用绑定约束法[18]。

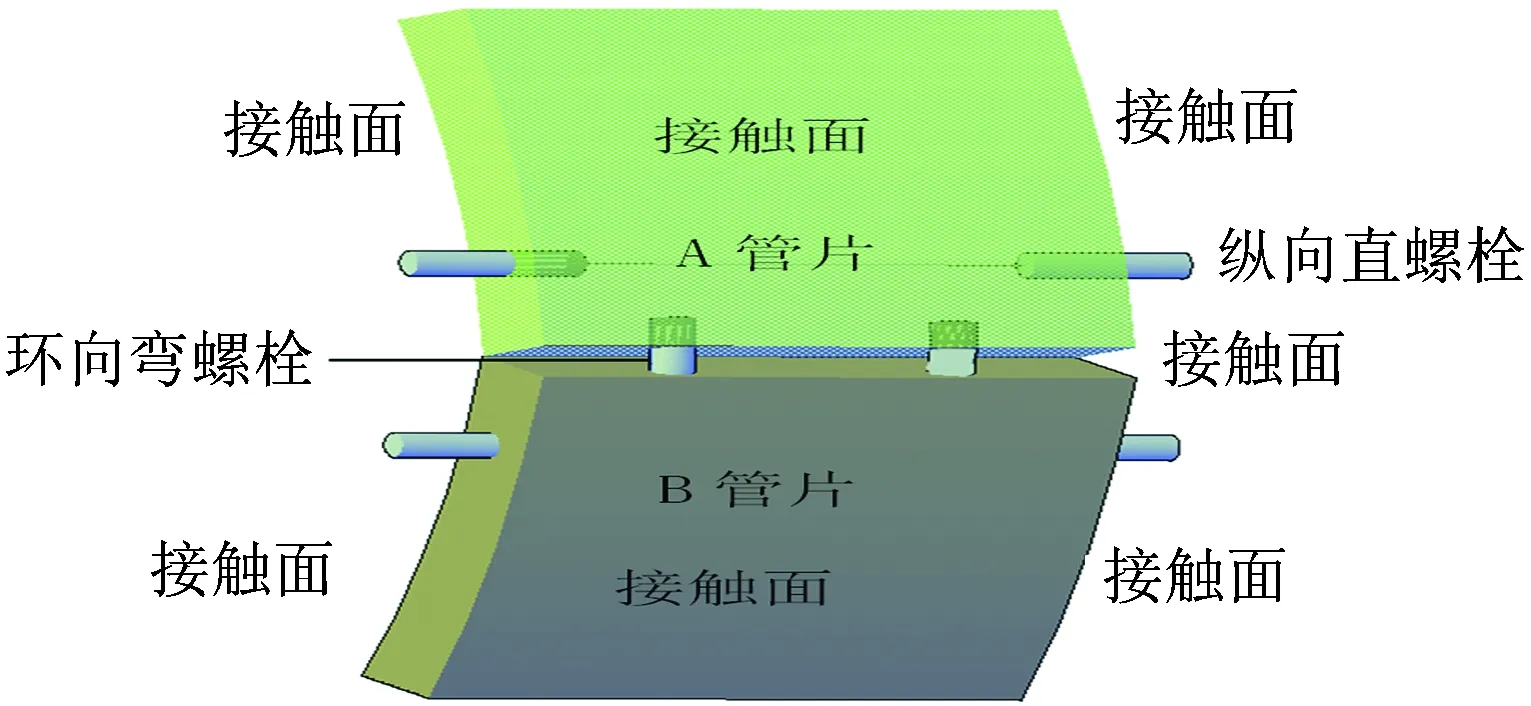
图2　拼装式管片衬砌接触模型局部示意

通过采用这些接触模型可以在较大程度上模拟盾构隧道接头之间以及隧道与围岩之间的接触关系，同时避免了过于精细化建模造成的计算困难。

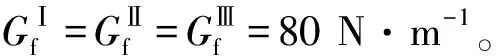
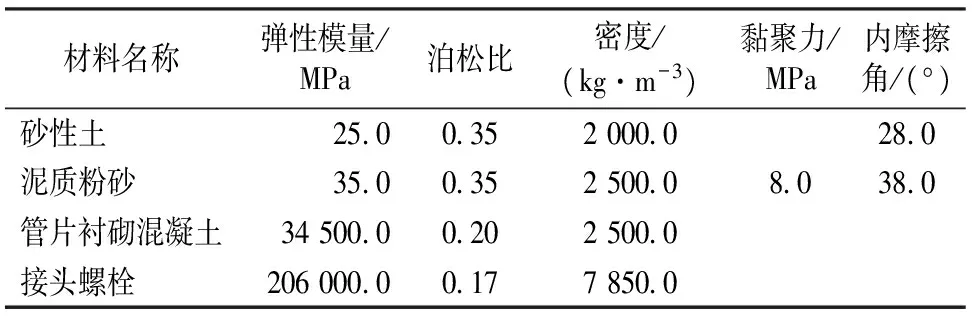
表1　材料参数

目前，列车撞击荷载主要基于列车—刚性墙撞击三维模型通过数值分析方法获得。研究表明，列车斜向撞击荷载主要与列车编组、撞击速度和撞击角度有关[6]。文献[7]给出了列车为8辆编组、运行速度为200 km·h-1、脱轨撞击角度为12.5°的列车撞击力时程曲线，如图3所示，有效撞击时间持续32 ms；本文以1.2 ms为界，将包括峰值所在的前1.2 ms视为荷载峰值阶段，1.2 ms之后视为荷载震荡阶段。将图3中列车斜向撞击力荷载分解为x，y，z这3个方向的分力，并将分力按实际撞击位置和作用范围以平均面力的近似形式施加在管片衬砌内表面。

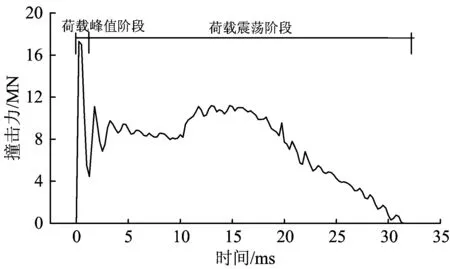
图3　200 km·h-1列车斜向撞击荷载时程曲线

图4为撞击中心区域附近管片衬砌环和接头螺栓的编号图，图中标示出了列车行驶方向、撞击区域中心。为便于讨论，将通缝拼装的管片衬砌环分别编为①，②，③号，其中②号是撞击目标环。J1，J2，J3为拼装管片衬砌环时的3条纵向接缝，撞击区域中心位于封顶块下方的邻接块上，且与J1接缝的距离为1/3邻接块弧长。M1和M2为J2接缝上目标环的2颗环向螺栓，M3和M4为J3接缝上目标环的2颗环向螺栓，L1和L2为目标环封顶块上的前后2颗纵向螺栓，L3和L4为目标环上撞击目标块(邻接块)的前后2颗纵向螺栓。

图4　管片衬砌环和接头螺栓的编号

3　盾构隧道管片衬砌开裂特性

3.1　管片衬砌裂缝分布

在列车撞击荷载作用下，管片衬砌出现开裂的位置主要集中在管片的撞击中心区域，以及J2接缝和J3接缝部位，如图5所示。由于出现在管片撞击中心区域的那条裂缝较长且为管片内外表面贯穿性裂缝，因而将其命名为主裂缝，其对衬砌破坏起主要控制作用；在J2接缝部位有2条裂缝，J3接缝部位有4条裂缝，均出现在接缝面或者紧邻接缝面的管片外侧。

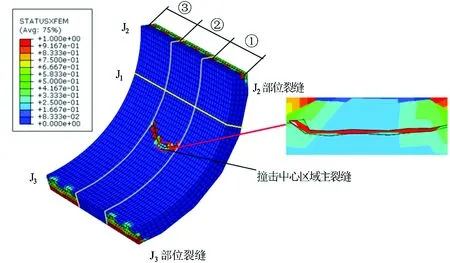
图5　3个重点部位的管片裂缝分布

图6为列车撞击荷载作用下撞击中心区域开裂的过程图。由图6可知：撞击荷载作用1.47×10-2ms后，撞击区域中心的管片衬砌内表面率先出现开裂，随着撞击荷载的持续作用，开裂逐渐斜向上往两侧延展，最终形成管片衬砌内侧的主裂缝；管片衬砌外侧主裂缝率先在0.150 ms时出现在撞击区域中心靠近L3直螺栓部位，进而在撞击中心另一侧出现微裂缝，最终由两侧微裂缝斜向下延伸，形成管片衬砌外侧主裂缝，并与管片衬砌内侧主裂缝形成贯穿性裂缝。利用分析软件的度量功能，可知内侧主裂缝的长度为2.648 m，外侧的长度为2.789 m，外侧比内侧稍长。从内、外侧主裂缝扩展分布情况还可以看出，主裂缝未能向撞击目标环前后两侧的邻近衬砌环进一步扩展，这主要是由于受到衬砌环向接缝的影响。

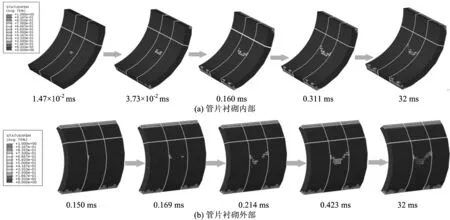
图6　撞击中心区域管片衬砌开裂过程

图7为J2接缝和J3接缝部位裂缝的最终分布情况。由图7可见：接缝部位的裂缝主要分布在接缝面和邻近接缝面的管片衬砌外侧；在J2接缝部位，3个衬砌环的各环接缝面和邻近其管片衬砌外侧的裂缝长度均为2.0 m；在J3接缝部位，其撞击目标环并未出现裂缝，而邻近的前后衬砌环接缝面裂缝长度大致为2.355 m，邻近接缝面管片衬砌外侧裂缝长度大致为2.586 m，这是由于J3接缝部位与中心的相对位置与J2不同，使得受力破坏机理亦有所不同。

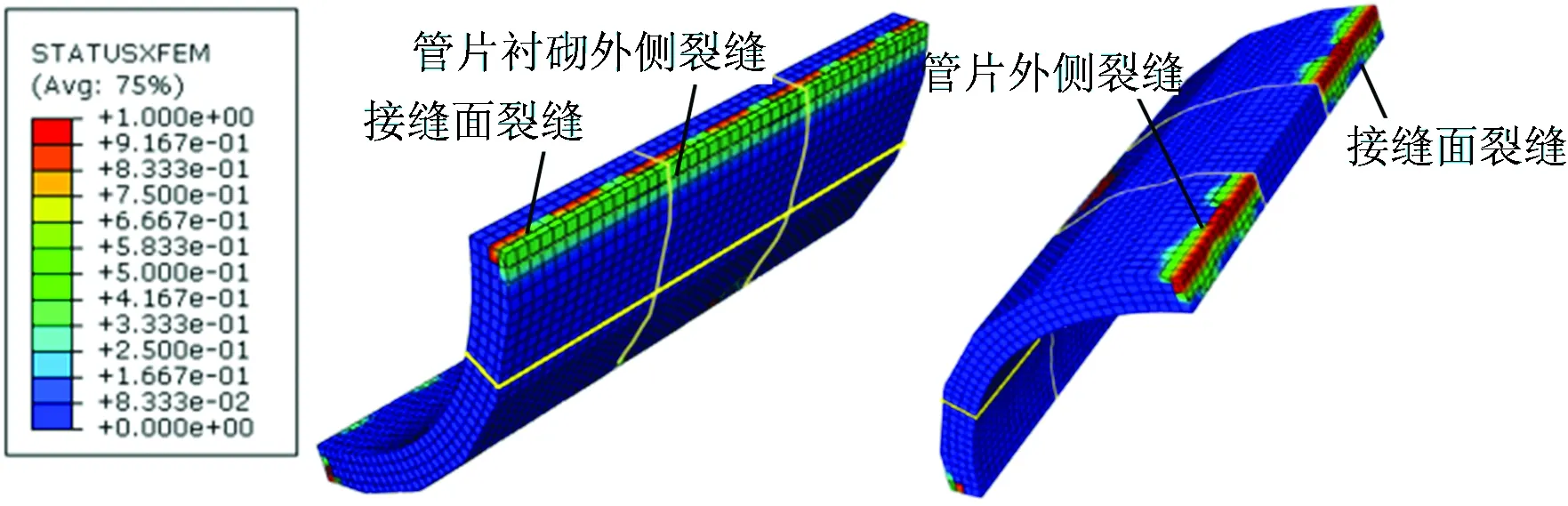
图7　J2接缝和J3接缝部位裂缝的最终分布

3.2　管片衬砌裂缝张开度

沿列车行进方向，在内侧主裂缝依次布置A1—A6数值监测点；在J2接缝部位接缝面裂缝依次布置B1—B3数值监测点，在管片衬砌外侧裂缝依次布置B4—B6数值监测点，B1—B6数值监测点均位于3环管片各环管片纵向接缝中间位置；J3接缝部位裂缝主要集中在衬砌环①和③，且裂缝分布大致相同。选取③号衬砌环的裂缝进行张开度分析，在接缝面裂缝弯螺栓处以及管片中心处依次布置C1—C3数值监测点，在管片衬砌外侧裂缝的相对位置依次布置C4—C6数值监测点。由图6可以看出，主裂缝为不规则曲线裂缝；J2接缝部位裂缝为2条，出现在3环管片上且为直线裂缝；J3接缝部位裂缝为折线裂缝，位于同一侧的各个数值监测点并不在一条直线上。各部位裂缝数值监测点位置如图8所示。

图8　各部位裂缝的数值监测点

图9为管片衬砌内侧主裂缝各数值监测点张开度的时程曲线。由图9可知：距离撞击中心较远的A1，A5，A6数值监测点的峰值张开度出现在荷载震荡阶段，其值较小，随着撞击力的减小和消散，其张开度并未出现较大的变化；距离撞击中心较近的A2，A3，A4数值监测点的峰值张开度也出现在荷载峰值阶段，但其值较大，且随着撞击力的减小和消散而迅速缩小，并在经过一段时间的震荡回升之后闭合，最终其张开度略大于A1，A5，A6数值监测点。

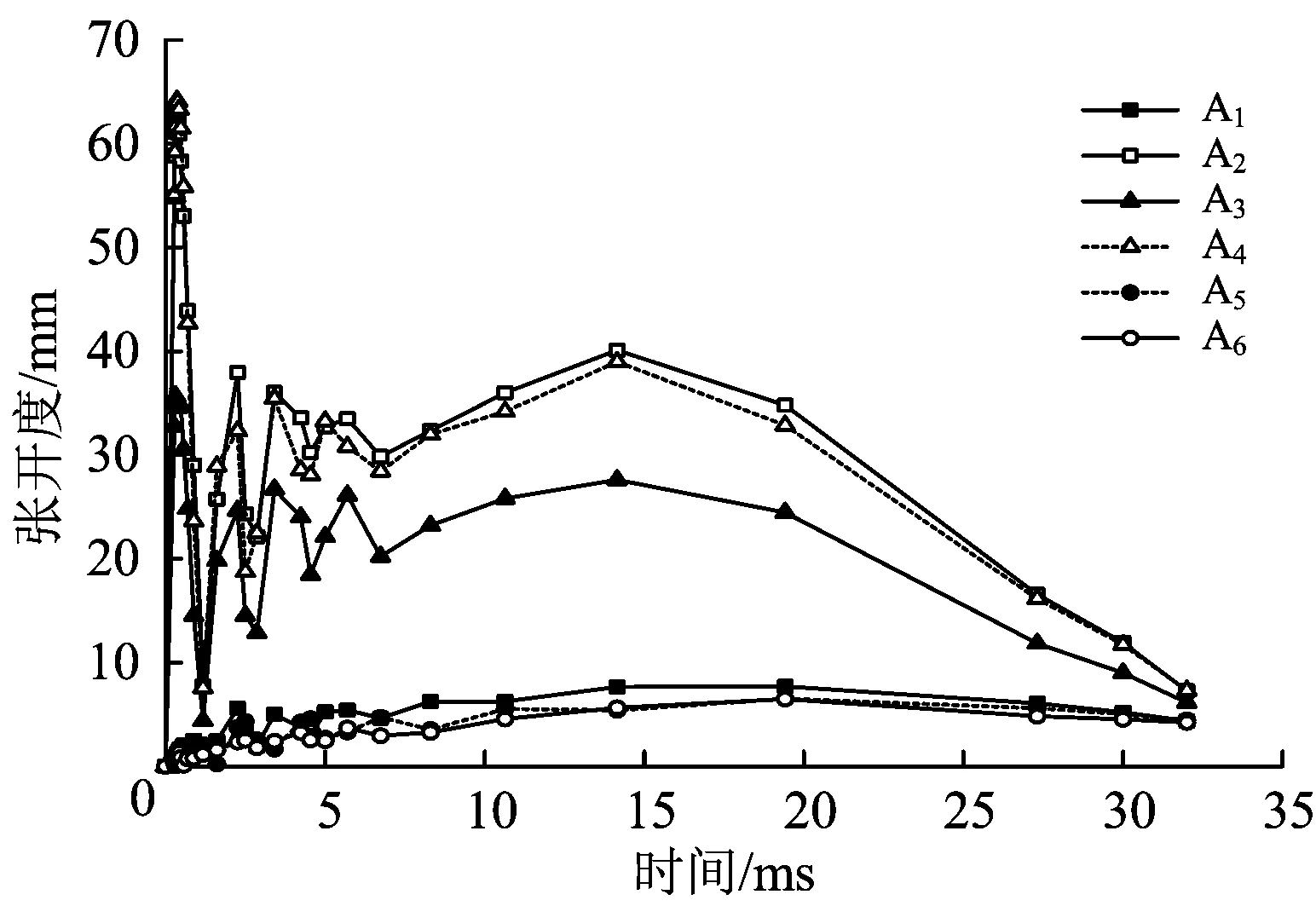
图9　内侧主裂缝各数值监测点的张开度时程曲线

表2为内侧主裂缝各数值监测点的张开度统计表。由表2可知：A2，A3和A4数值监测点的峰值张开度为A1，A5，A6数值监测点的5～10倍，而随着撞击力减小直至消散，其最终张开度仅为A1，A5和A6数值监测点的1～2倍；沿裂缝长度方向的最终张开度分布相对均匀；位于撞击区域中心的A3数值监测点的峰值张开度和最终张开度均小于相邻的A2和A4数值监测点，可能原因是撞击区域中心处管片主要遭受压力而非拉力。

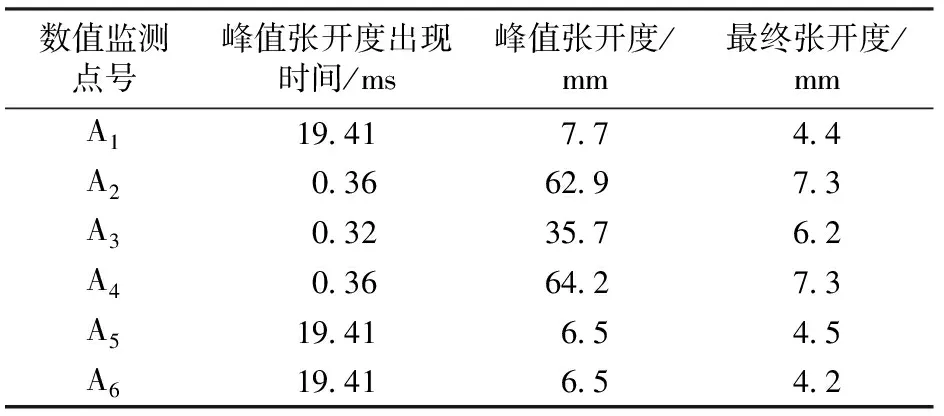
表2　内侧主裂缝各数值监测点张开度统计表

图10为J2接缝和J3接缝部位裂缝各数值监测点张开度的时程曲线。由图10可知：在撞击力的作用下，张开度均逐渐增大并且在荷载作用末段略有下降，峰值张开度均出现在荷载震荡作用阶段，各数值监测点张开度时程曲线整体变化规律差别不大；对于同一部位，邻近接缝面的管片衬砌外侧裂缝张开度均大于接缝面裂缝；且外侧裂缝和接缝面裂缝的张开度较为接近，表明裂缝张开较为均匀；相对J2接缝部位而言，J3接缝部位沿裂缝长度方向张开度分布更加均匀，接缝面裂缝与邻近接缝外表面裂缝张开度之间的差异较J2接缝部位要小。

表3为J2接缝和J3接缝部位各数值监测点的裂缝张开度表。从表3可知：接缝部位裂缝的峰值张开度和最终张开度最大值均出现在衬砌环②的J2接缝部位B5数值监测点处。对比表3与表2可知：撞击中心区域裂缝峰值张开度大于J2接缝和J3接缝部位，但最终张开度最大的裂缝为J2接缝部位临近接缝面的管片衬砌外侧裂缝。

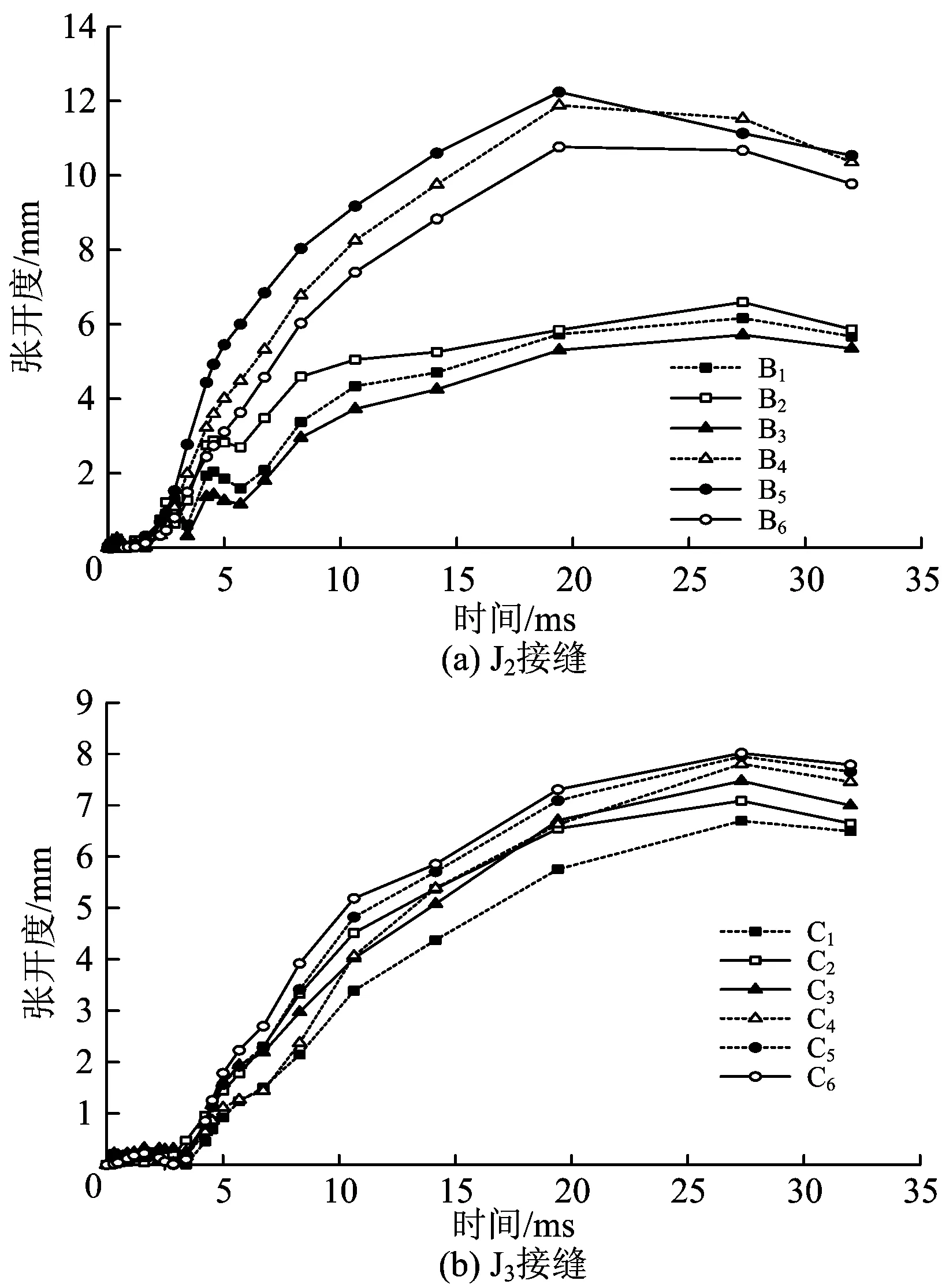
图10　J2和J3接缝部位各数值监测点张开度的时程曲线

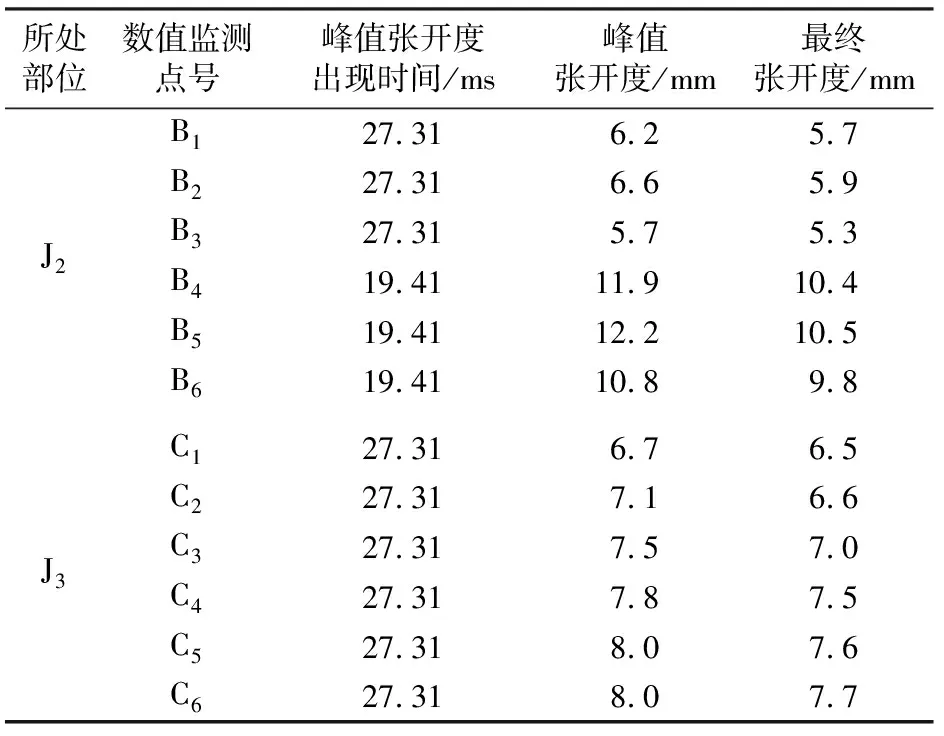
所处部位数值监测点号峰值张开度出现时间/ms峰值张开度/mm最终张开度/mmJ2B127316257B227316659B327315753B41941119104B51941122105B6194110898J3C127316765C227317166C327317570C427317875C527318076C627318077

4　接头螺栓动力响应特性

为分析接头螺栓的动力响应特性，选取②号衬砌环的J2接缝、J3接缝的M1—M4的4个弯螺栓和L1—L4的4个直螺栓进行分析，这8颗螺栓均取螺杆中间截面的中心位置为数值监测点。

图11为管片接头螺栓最大主应力时程曲线。从图11可知：螺栓的最大主应力在荷载峰值阶段表现为明显的震荡现象，在荷载震荡阶段则随着撞击力作用的持续时间呈现先快速增大，达到峰值后缓慢回落，最大主应力峰值出现在荷载震荡阶段，在撞击力作用完成时，螺栓最大主应力仍处于较高的水平；位于同一水平线上的螺栓，处于撞击中心区域后侧的螺栓的最大主应力大于前侧(列车前进方向)的，即J2接缝部位M1螺栓的最大主应力大于M2螺栓的，J3接缝部位M3螺栓的最大主应力大于M4螺栓的，直螺栓中L1螺栓的最大主应力大于L2螺栓的，L3螺栓的最大主应力大于L4螺栓的，这是由列车的斜向撞击作用，所施加的荷载与衬砌表面呈一定的角度所导致的。

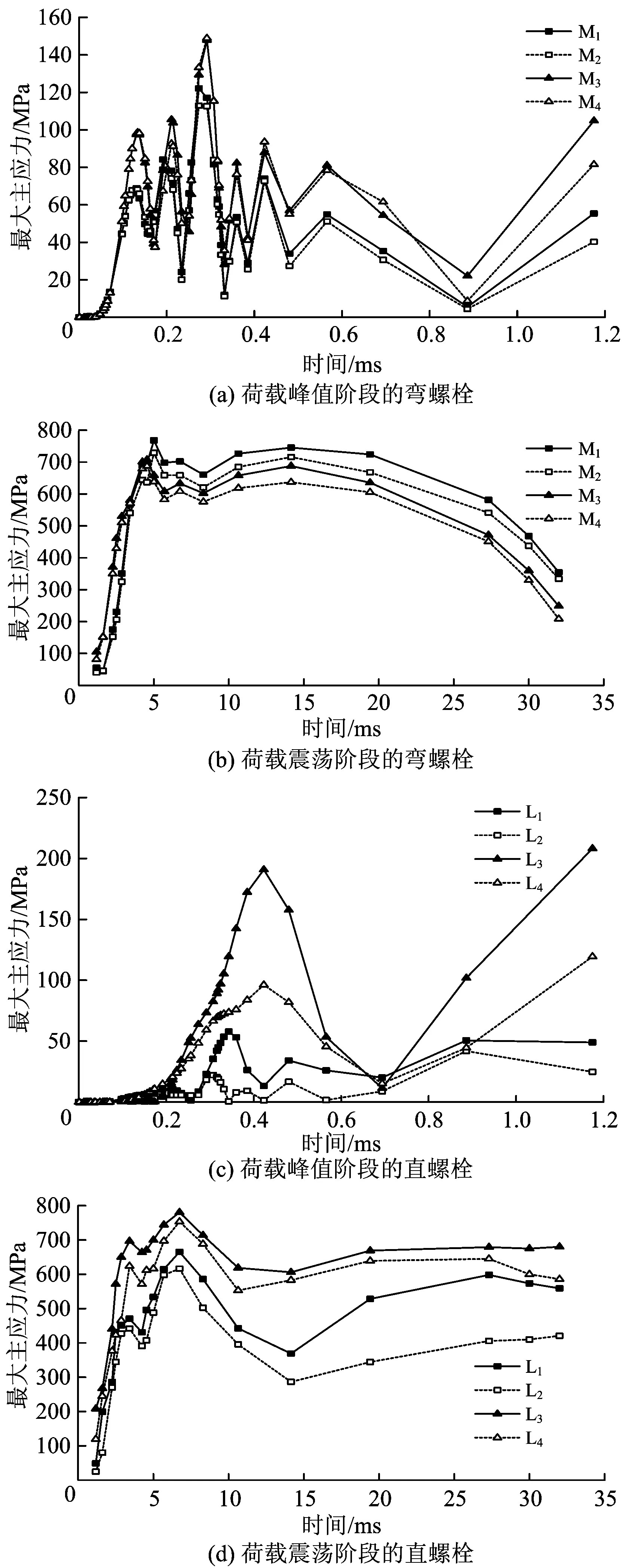
图11　接头螺栓最大主应力时程曲线

图12为接头螺栓振动速度时程曲线。从图12可知：螺栓的峰值振动速度出现在荷载震荡阶段，在达到峰值后逐渐回落，由于列车的斜向撞击作用，位于同一水平线上后侧螺栓的振动速度大于前侧螺栓的；在荷载峰值阶段，J3接缝部位M3和M4弯螺栓的振动速度大于J2接缝部位M1和M2弯螺栓的，而在荷载震荡作用阶段则相反；距离撞击区域中心较近的L3和L4直螺栓的振动速度大于较远处L1和L2直螺栓的。

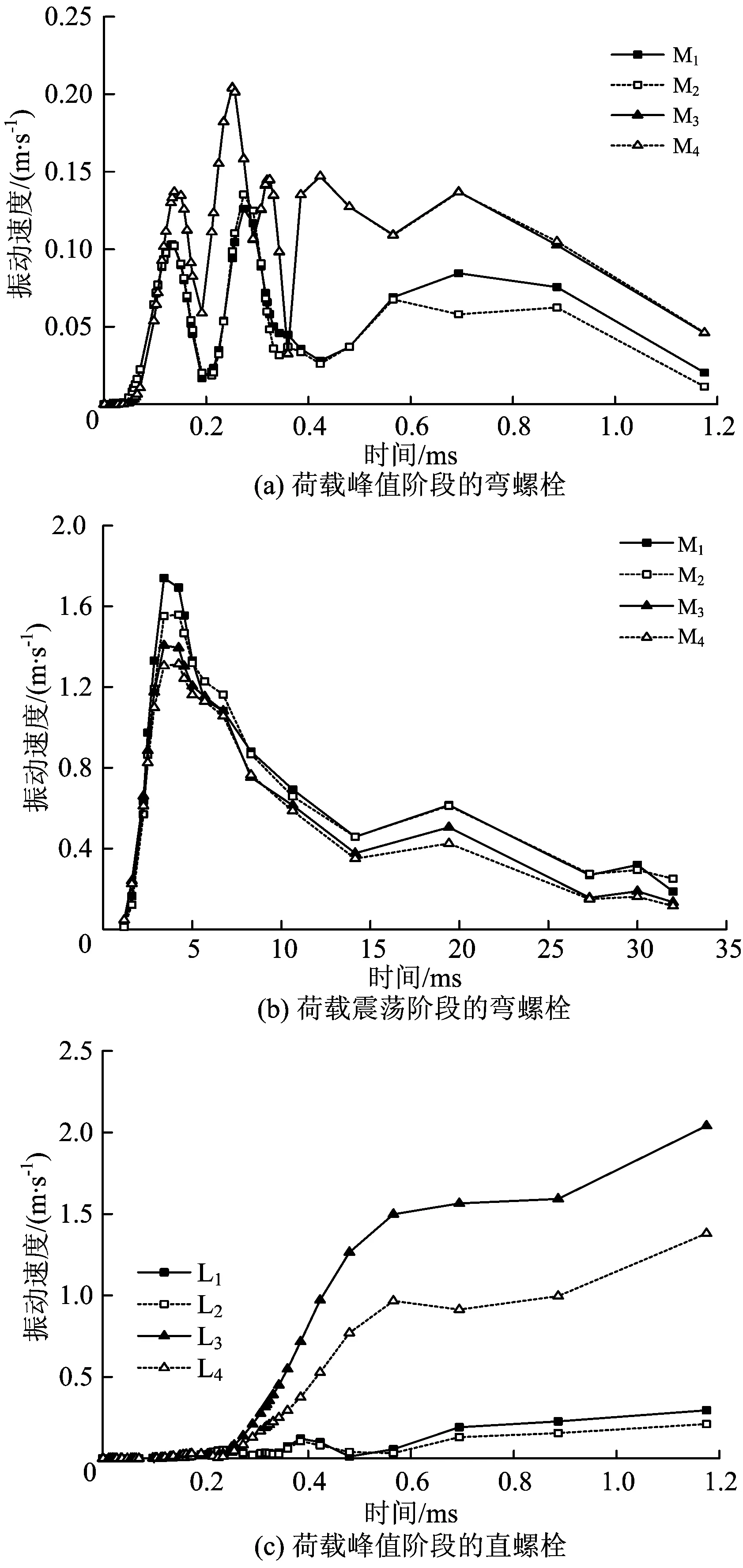
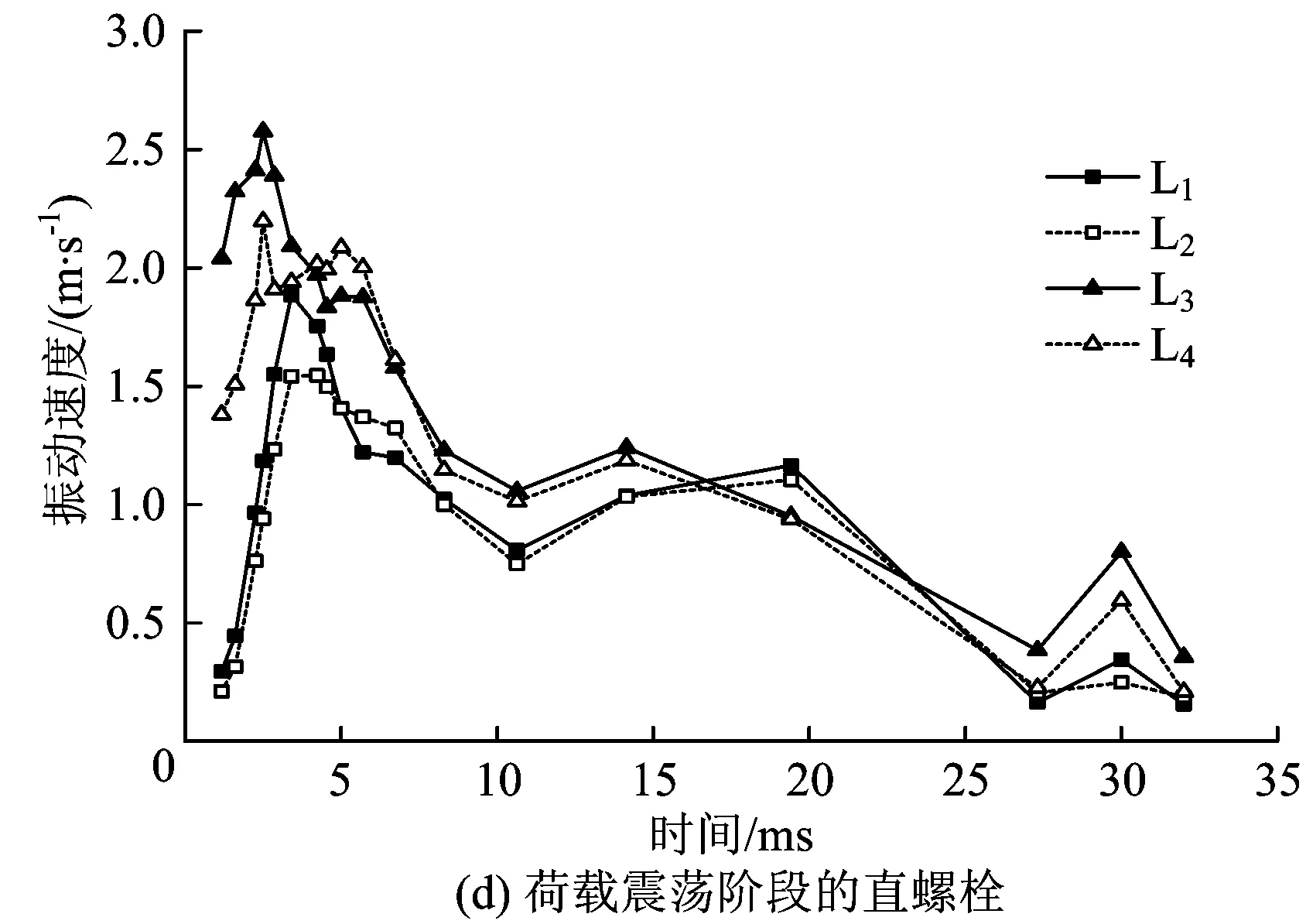
图12　接头螺栓振动速度时程曲线

图13为接头螺栓振动加速度时程曲线。从图13可知：位于同一水平线上后侧螺栓的振动加速度大于前侧螺栓的，与最大主应力和振动速度不同，振动加速度峰值出现在荷载峰值阶段，并且随着撞击力峰值的消散，螺栓的振动加速度迅速减小，并在撞击荷载作用的后20 ms一直保持在较低水平，说明螺栓振动加速度主要受峰值荷载的影响，后续震荡荷载并未使接头螺栓产生较大的振动加速度响应；在荷载峰值阶段，J3接缝部位M3和M4弯螺栓的振动加速度明显大于J2部位M1和M2弯螺栓的；靠近撞击区域中心处L3和L4直螺栓振动加速度大于较远处L1和L2直螺栓的。

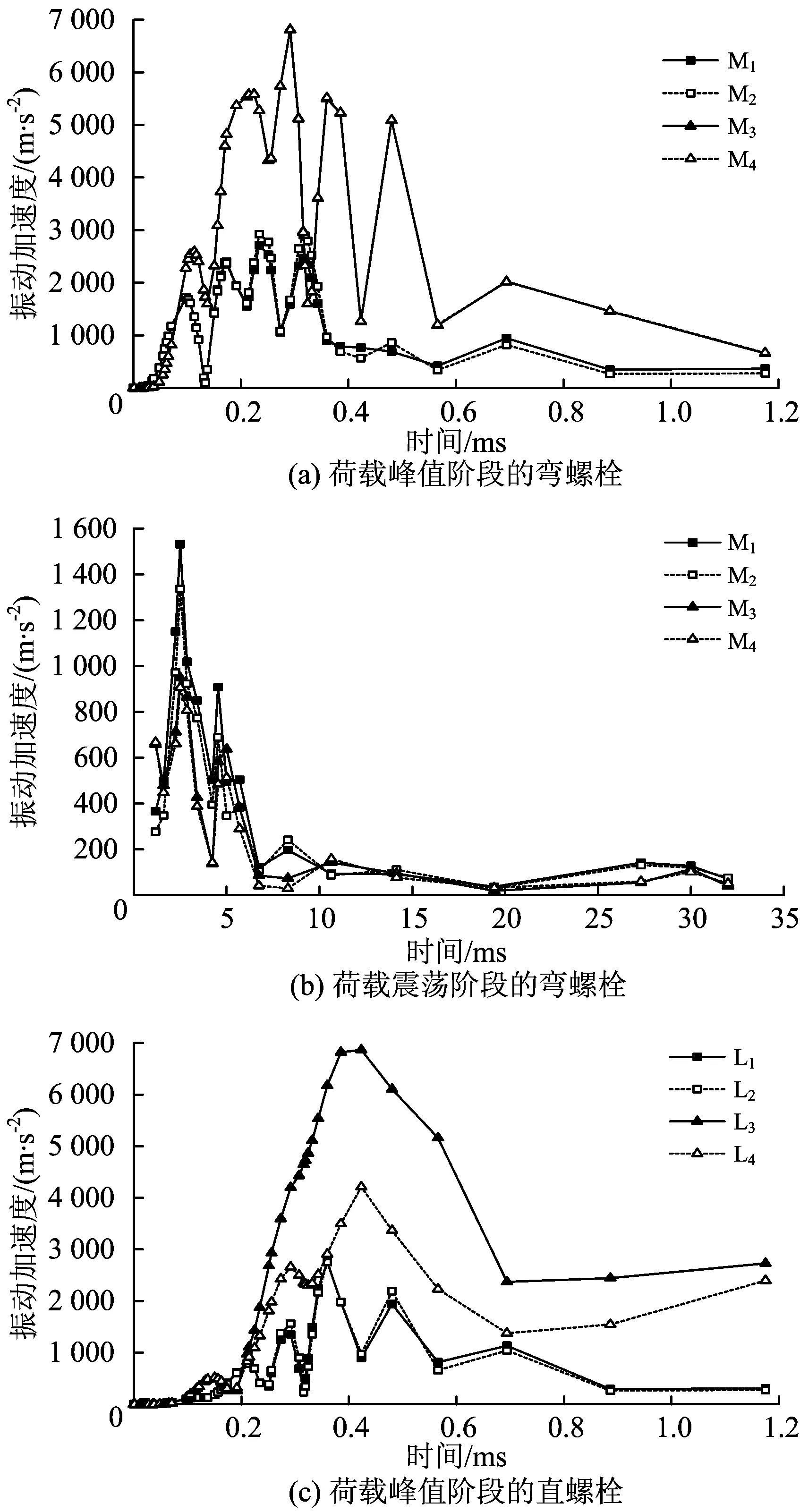
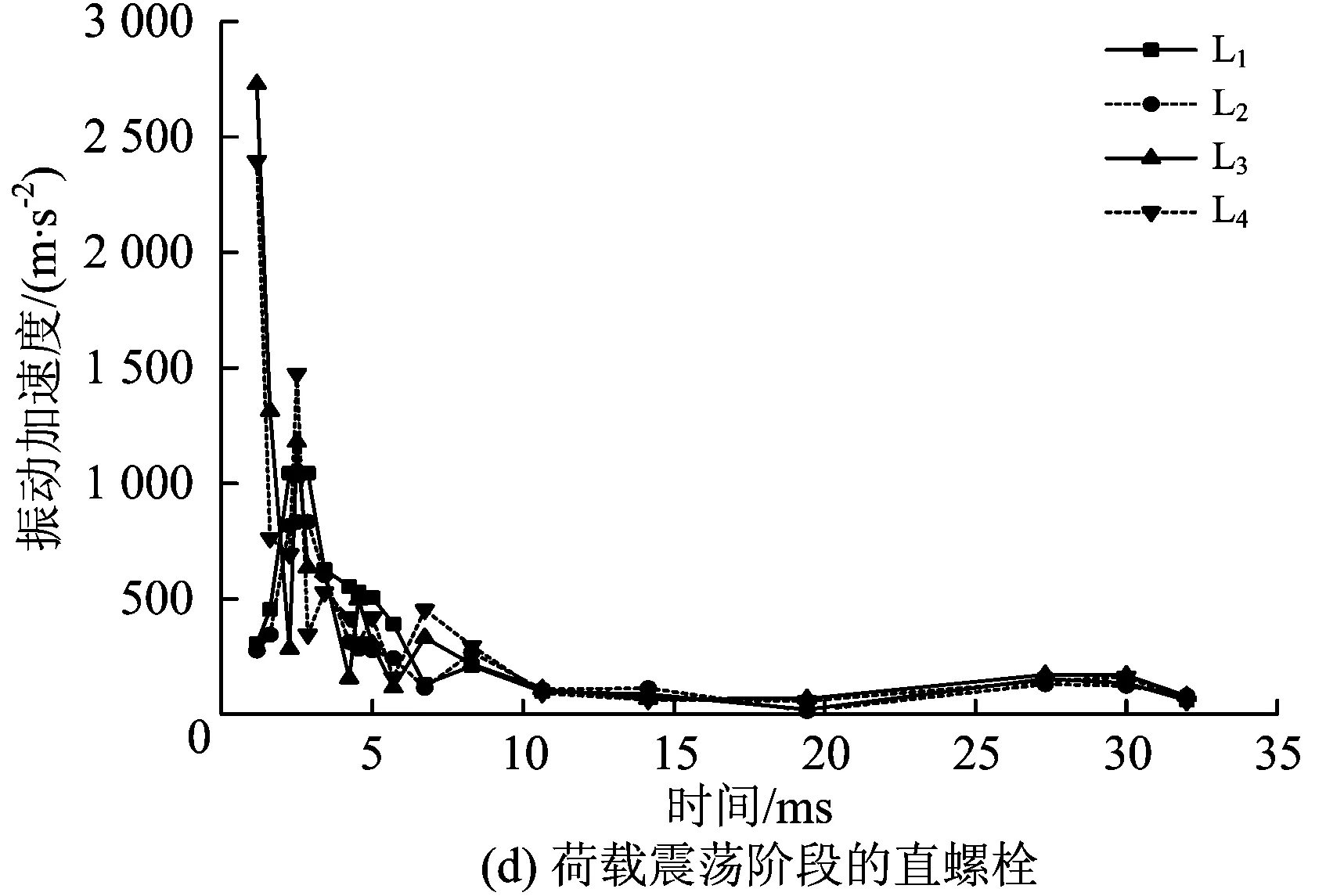
图13　接头螺栓振动加速度时程曲线

5　结　论

(1)在列车撞击荷载作用下，管片衬砌的开裂主要集中在管片撞击中心区域及其附近纵向接缝部位。撞击中心区域内表面裂缝是从撞击区域中心初始裂缝开始，然后斜向上向两侧扩展形成的，而外表面裂缝则是在撞击区域中心两侧分别出现初始裂缝，然后各自斜向下向撞击中心扩展相连形成的，撞击中心区域裂缝为贯穿性不规则曲线裂缝；纵向接缝部位裂缝出现在接缝面以及紧邻接缝面的管片衬砌外侧，位于撞击中心区域上方纵向接缝部位的裂缝通常呈现为直线裂缝，而位于撞击中心区域下方纵向接缝部位的裂缝则通常为多段折线裂缝。

(2)管片撞击中心区域裂缝的张开度与距撞击区域中心的距离有关，距离撞击区域中心较近位置的峰值张开度是距离较远位置的峰值张开度的5～10倍，但最终张开度较为接近，表明其最终张开形态较为均匀；撞击中心区域裂缝在撞击区域中心处的峰值张开度和最终张开度都小于前后邻近部位。

(3)纵向接缝部位裂缝张开度随着撞击荷载的持续作用逐渐增大，达到峰值后略有减小，紧邻接缝面管片衬砌外侧裂缝的张开度大于接缝面上裂缝的张开度；对于撞击中心区域和纵向接缝部位的裂缝而言，最大峰值张开度出现在撞击中心区域裂缝上，而最大最终张开度出现在纵向接缝部位裂缝上。

(4)在整个撞击过程中，弯螺栓(环向螺栓)和直螺栓(纵向螺栓)的动力响应呈现出不同的变化规律；螺栓最大主应力、振动速度峰值均出现在荷载震荡作用阶段，而振动加速度峰值则出现在荷载峰值阶段；位于同一水平线上撞击区域后侧螺栓的最大主应力、振动速度和振动加速度等动力响应总是大于前侧螺栓的。

[1]JEONG-Seo Koo，TAE-Soo Kwon，HYUN-Jik Cho. 韩国高速列车防撞设计与评估[J]. 中国铁道科学，2004，25(1)：1-7.

(JEONG Seo Koo，TAE Soo Kwon，HYUN Jik Cho.Korean High-Speed Railway Anti-Impact Structure Design and Appraisal[J].China Railway Science，2004，25(1):1-7.in Chinese)

[2]刘金朝, 房加志, 王成国，等. 铁道客车大变形碰撞仿真研究[J]. 中国铁道科学, 2004, 25(6):1-8.

(LIU Jinzhao，FANG Jiazhi，WANG Chengguo, et al.Simulation Research on Finite Deformation Crashworthiness of Railway Passenger Car[J].China Railway Science，2004，25(6):1-8.in Chinese)

[3]TYRELL D, JACOBSEN K, PARENT D. Preparations for a Train-to-Train Impact Test of Crash-Energy Management Passenger Rail Equipment[C]// Proceedings of the 2005 ASME/IEEE Joint IEEE. Pueblo Colorado: IEEE, 2005:107-116.

[4]姚松，田红旗. 车辆吸能部件的薄壁结构碰撞研究[J]. 中国铁道科学，2001，22(2):55-60.

(YAO Song，TIAN Hongqi.Crash Research on Thin-Shelled Structure as Vehicle Energy-Absorbing Components[J].China Railway Science，2001，22(2):55-60.in Chinese)

[5]向俊，龚凯，毛建红，等. 高速列车运行安全性与桥梁防撞墙受力分析[J]. 铁道学报，2011，33(12):83-87.

(XIANG Jun，GONG Kai ，MAO Jianhong，et al.Analysis on the Running Safety of High-Speed Train and the Force of Bridge Collision-Proof Wall[J].Journal of the China Railway Society，2011，33(12):83-87.in Chinese)

[6]YAN Qixiang, LI Bin, GENG Ping, et al. Dynamic Response of a Double-Lined Shield Tunnel to Train Impact Loads[J]. Tunnelling & Underground Space Technology, 2016, 53:33-45.

[7]晏启祥，李彬，张蒙，等. 200 km·h-1列车脱轨撞击作用下盾构隧道二次衬砌对管片衬砌的防护效果[J]. 中国铁道科学，2014，35(6):70-78.

(YAN Qixiang，LI Bin，ZHANG Meng，et al. Protective Effect of Secondary Lining of Shield Tunnel on Segment Lining under Derailment Impact at the Speed of 200 km·h-1[J].China Railway Science，2014，35(6):70-78.in Chinese)

[8]晏启祥, 李彬, 张蒙，等. 列车撞击荷载的有限元数值分析[J]. 西南交通大学学报, 2016, 51(1):1-7.

(YAN Qixiang，LI Bin，ZHANG Meng，et al. Numerical Analysis of Train Impact Load with Finite Element Method[J].Journal of Southwest Jiaotong University, 2016, 51(1):1-7. in Chinese)

[9]晏启祥, 李彬, 张蒙,等. 列车撞击荷载下盾构隧道双层衬砌管片结构的动力响应特性[J]. 中南大学学报:自然科学版, 2015(9):3527-3534.

(YAN Qixiang，LI Bin，ZHANG Meng，et al. Dynamic Response of Segment Structure of Double Lining Shield Tunnel under Train Impact Load [J]. Journal of Central South University:Science and Technology, 2015(9):3527-3534. in Chinese)

[10]BELYTSCHKO T, BLACK T. Elastic Crack Growth in Finite Elements with Minimal Remeshing[J]. International Journal for Numerical Methods in Engineering, 1999, 45(5):601-620.

[11]WELLS G N, SLUYS L J. A New Method for Modelling Cohesive Cracks Using Finite Elements[J]. International Journal for Numerical Methods in Engineering, 2001, 50(12):2667-2682.

[12]NICOLAS Mo⊇s, BELYTSCHKO T. Extended Finite Element Method for Cohesive Crack Growth[J]. Engineering Fracture Mechanics, 2002, 69(7):813-833.

[13]方修君，金峰，王进廷，等. 基于扩展有限元法的粘聚裂纹模型[J]. 清华大学学报:自然科学版，2007，47(3):344-347.

(FANG Xiujun，JIN Feng，WANG Jinting，et al.Cohesive Crack Model Based on Extended Finite Element Method[J]. Journal of Tsinghua University：Science and Technology，2007，47(3):344-347.in Chinese)

[14]RÉTHORÉ J， GRAVOUIL A，COMBESCURE A. An Energy-Conserving Scheme for Dynamic Crack Growth Using the Extended Finite Element Method[J]. International Journal for Numerical Methods in Engineering, 2005, 63(5):631-659.

[15]ZI G, CHEN H, XU J, et al. The Extended Finite Element Method for Dynamic Fractures[J]. Shock & Vibration, 2005, 12(1):9-23.

[16]郭历伦，陈忠富，罗景润，等. 扩展有限元方法及应用综述[J]. 力学季刊，2011，32(4)：612-625.

(GUO Lilun，CHEN Zhongfu，LUO Jingrun，et al.A Review of the Extended Finite Element Method and Its Applications [J].Chinese Quarterly of Mechanics，2011，32(4)：612-625.in Chinese)

[17]方修君，金峰. 基于ABAQUS平台的扩展有限元法[J]. 工程力学，2007，24 (7)：6-10.

(FANG Xiujun，JIN Feng.Extended Finite Element Method Based on ABAQUS[J]. Engineering Mechanics，2007，24 (7)：6-10.in Chinese)

[18]赵武胜，何先志，陈卫忠，等. 盾构隧道地震响应分析方法及工程应用[J]. 岩土力学，2012，33(8)：2415-2421.

(ZHAO Wusheng，HE Xianzhi，CHEN Weizhong，et al.Method for Analyzing Seismic Response of Shield Tunnel and Its Application[J].Rock and Soil Mechanics，2012，33(8)：2415-2421.in Chinese)

[19]中华人民共和国住房和城乡建设部. GB 50010—2010 混凝土结构设计规范[S]. 北京：中国建筑工业出版社，2010.

[20]王金昌，陈页开.ABAQUS 在土木工程中的应用[M].杭州:浙江大学出版社，2006.