动力对全机水滴收集率的影响计算

王开春，易贤，马洪林，赵凡

(中国空气动力研究与发展中心空气动力学国家重点实验室，四川绵阳621000)

动力对全机水滴收集率的影响计算

王开春，易贤，马洪林*，赵凡

(中国空气动力研究与发展中心空气动力学国家重点实验室，四川绵阳621000)

针对飞机在飞行中遭遇过冷水滴撞击并结冰现象，建立了适合于发动机带动力情况下结冰过程水滴收集率计算的三维数值方法和计算程序。其基本思路为:采用多块技术与SIMPLE方法计算空气流场，以流场分布的计算结果为基础，求解水滴相的控制方程，进而获得物体表面的水滴收集率。空气相控制方程和水滴相控制方程均写成典型输运方程的形式，采用一致的有限体积法离散求解，方便了计算程序的编制。对某型运输机巡航构型有/无动力条件的水滴收集率进行了比较计算，获得了不同直径水滴在飞机表面的撞击特征以及水滴收集率在飞机机翼、平尾、垂尾和发动机进气道唇口上的分布规律。研究表明:(1)发动机是否带动力对机翼、平尾、垂尾的水滴收集率基本无影响;(2)飞机带动力主要影响发动机进气道唇口处的水滴收集率，带动力后唇口的收集率比无动力情况高，水滴撞击范围增大，在进行防除冰研究和设计时需引起重视。

飞机;动力影响;结冰;水滴收集率;数值计算

0 引言

飞机在飞行过程中，如果遇到含有过冷水滴的气流，在飞机表面如机翼、垂直尾翼、水平尾翼、机头雷达罩、发动机进气道唇口等处会发生结冰现象［1］。飞机的机翼、垂直尾翼、水平尾翼等处结冰会改变飞机的气动外形，破坏飞机的流场特性与飞机气动性能，对飞机的安全性造成影响［2-3］。同样，发动机进气道唇口结冰，会导致进气道流场产生分离，流场畸变指数增加，破坏进气道流场品质，造成安全隐患［4］。

水滴收集率(也称水滴局部收集系数)定义为飞机某局部区域实际所收集的水量与该区域可能收集的水量最大值之比，它表征了部件表面的水滴撞击范围以及撞击区域内水量的分布。水滴收集率是结冰研究中最重要的参数之一，只有获得水滴收集率，才能进行防/除冰系统设计。目前的防/除冰系统设计，多是基于飞机不带动力情况下的水滴收集率，但飞机在实际飞行中是带有动力的。飞机带动力后，发动机进气道入口产生了强大的抽吸效应，尾部会产生强烈的喷流效应，研究这些动力效应对水滴收集率以及对最终防除冰设计的影响具有重要的工程意义。目前尚未看到相关工作的公开报道。

为了进一步满足型号设计的需求，本文在前期发展的飞机结冰三维计算方法的基础上［5-9］，建立了适合于飞机带动力情况下结冰过程水滴收集率计算的三维数值方法和计算程序。并开展了某运输机发动机带动力对全机水滴收集率影响的研究，获得了不同攻角、不同水滴直径在飞机有/无动力情况下水滴收集率在飞机表面上的分布规律，为飞机各部件的防除冰设计提供了技术支撑。

1 数值计算方法

1.1 空气流场计算方法

空气流场计算采用本课题组自主研制的低速流动计算软件WS3D［4，10］。该软件在航空与航天飞行器起降气动特性、大型军用及民用运输飞机增升装置与各种操纵面的性能与载荷计算、舰尾流与飞机着舰、潜艇、汽车、磁浮列车、高铁与城际列车、风力机等方面的计算中得到广泛地应用。

低速流动的控制方程为不可压N-S方程，其通用形式为:

方程(1)中，φ为输运变量，ρa为空气密度，va为空气速度，Γφ为扩散系数，qφ为源项，φ、Γφ和qφ取不同值，可代表空气的连续性方程、动量方程和其他标量(如温度、湍动能等)的输运方程。

数值计算方法为:采用有限体积法离散，离散后方程组求解采用SIP强隐式算法;不可压的计算方法采用SIMPLE系列算法;采用结构网格的多块对接技术与多窗口技术处理复杂外形和边界;湍流计算采用两方程的k-ε模型，近壁区采用低Re数修正与壁面函数相结合的方法处理。通常的边界条件有四种类型:对称边界条件、入流边界条件、固壁边界条件和出口边界条件。方程中各项的物理意义、具体表达式以及数值方法可参见文献［4，14-15］。

对于涡扇发动机带动力模拟，需要处理两种类型的边界条件:1)内、外涵道出口。本文采用入流条件处理。动力计算条件分别给出了内、外涵道出口处的总温和总压，由此可获得密度、速度，按常规的入流边界条件分别给定内、外涵道出口面上的速度与密度即可。2)进气道出口。本文采用流量修正方法处理。即在每步迭代计算过程中，都需要先计算流量修正系数Fac，其表达式为:

式中Fctr为发动机的进气量，由动力计算条件给定; Fout为进气道出口流量，其计算是利用常规的出口边界条件获得，即边界上速度与密度场的梯度为0。然后对进气道出口边界面上的速度进行修正，其方法为:

式中uout为进气道出口速度，为修正后的进气道出口速度。当计算迭代到一定步数后，计算的出口流量就与计算条件给定流量相等，也满足了进气道的出口流量条件。

1.2 水滴相计算方法

全机表面水滴收集率的计算，目前主要有两种方法，一种是拉格朗日法［11］，另一种是欧拉法［12-13］。本文采用本课题组发展的三维水滴收集率计算的欧拉方法［5］，该方法适合于复杂外形。欧拉方法中引入水滴容积分数α，其定义为空间微团中水滴相所占的体积比例。则水滴相的控制方程为:

方程(4)、(5)分别为连续方程与动量方程。vd为水滴相速度，K为惯性因子，表达式为:

式中:μa为空气动力粘性系数，d为水滴直径，CD为水滴阻力系数，Re为相对雷诺数，其表达式为:

水滴运动过程中，阻力随相对雷诺数变化而变化。本文采用如下公式确定阻力［4］:

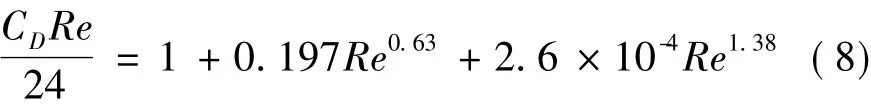
与空气控制方程类似，水滴相控制方程可以统一写成不包括扩散项的输运方程形式:

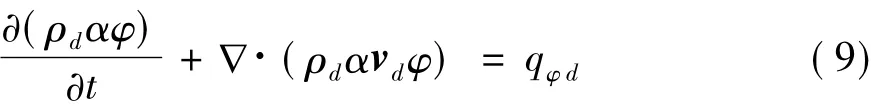
式中:qφd为源项，φ取1、vd分别代表连续方程和动量方程。

对于方程(9)采用有限体积方法离散，其中动量方程中的对流项和源项的离散方法与空气流场控制方程(1)一致，离散后的方程组求解方法也是一致的。水滴容积分数α通过求解连续方程获得，而连续方程的求解采用显式算法，其时间项采用一阶离散方法，即:

在水滴相计算中壁面采用吸入边界条件，即如果水滴与物面碰撞，则认为水滴从碰撞点流出。

对于发动机带动力模拟，需要处理两种类型的边界条件:1)发动机进气道出口处，采用常规的出口边界条件，即边界上水滴容积分数α与水滴速度的梯度为0;2)对于发动机内、外涵道出口处，采用常规的入流边界条件，给定水滴速度和容积分数，其中水滴速度与该处的空气喷流速度一致，而水滴容积分数值α为0。

由于水滴容积分数α较小(10-6量级)，可以认为空气和水滴是单向作用，即只考虑空气对水滴的作用，忽略水滴对空气的作用。因此，水滴收集率的计算步骤可概括为:(1)计算空气流场;(2)在得到空气流场分布的基础上，求解水滴相控制方程;(3)水滴收集率β可在获得当地水滴容积分数α和水滴与物面的相对速度ud之后，由以下表达式得到:

其中α∞为远场水滴容积分数，u∞为远场水滴速度，n为物面碰撞点处的单位法线向量。

2 带动力全机表面水滴收集率计算

基于以上数值方法开发了相应的飞机带动力条件下全机水滴计算程序，分别对某运输飞机巡航构型带动力模型、通气模型进行了应用计算。

2.1 计算外形及网格

计算外形为飞机半模，如图1。坐标原点取为机头中心，坐标轴方向为:x轴机身方向，y轴飞机高度方向垂直向上，z轴翼展方向按右手系确定。计算采用多块对接网格，网格规模为2.1×107。图2显示了通气模型与动力模型短舱尾部网格。

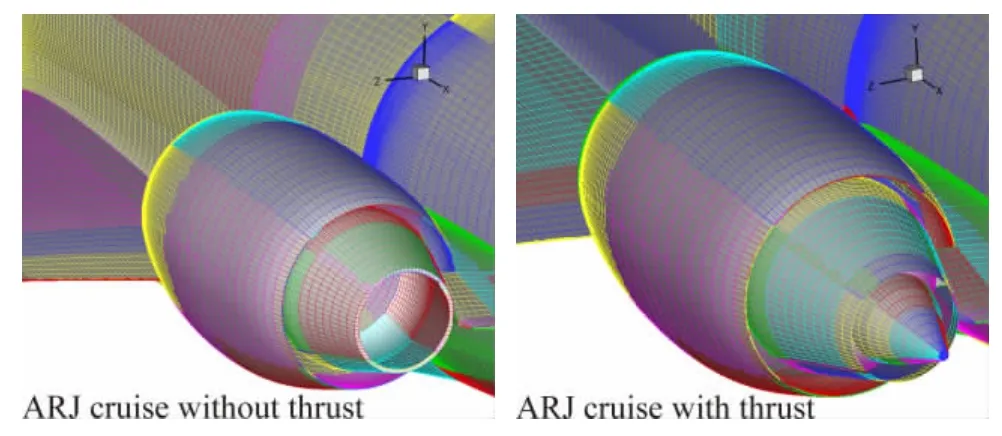
图2 两种模型短舱尾部表面网格Fig.2 Surface grid for the rear of the nacelle

2.2 飞机表面水滴收集率计算结果分析

在飞机空气流场计算的基础上，开展了水滴收集率计算，对比了不同直径水滴收集率在飞机表面的分布情况。计算条件为:飞行速度127 m/s，高度5200 m，发动机进气量Q=236.515 Ibm/s，飞机攻角三种α=2°、4°和6°，水滴直径选取了三种，从大到小分别为40、20、10μm。

图3给出了水滴直径d=40μm、攻角α=2°时通气模型和动力模型全机表面水滴收集率的分布云图，其中左图是通气模型，右图是带动力模型(下同)。计算显示:无论是否带动力，水滴撞击在飞机表面的主要部件均为机翼、垂直尾翼、水平尾翼、机头鼻尖、发动机进气道唇口等处。

图3 飞机有无动力表面水滴收集率云图(α=2°，d=40μm)Fig.3 Contours of collection efficiency on the airp lane surface w ith＆w ithout thrust(α=2°，d=40μm)

图4给出了水滴直径d=20μm、攻角α=4°时通气模型和动力模型发动机进气道唇口水滴收集率云图。图5给出了水滴直径d=20μm、攻角α=6°时通气模型和动力模型水滴运动轨迹与发动机进气道唇口水滴收集率云图。在飞机带动力后，由于发动机进气道内流量增加，流速也增加，并形成较高负压区，导致发动机唇口外侧的部分气流会被吸入进气道，形成抽吸效应。计算表明:(1)在动力模型的抽吸效应作用下，发动机进气道唇口处动力模型的水滴收集率分布与通气模型存在明显差别;(2)动力模型水滴收集率值明显比通气模型大一些;(3)在相同动力模型条件下，发动机进气道上唇口的收集率高于下唇口。

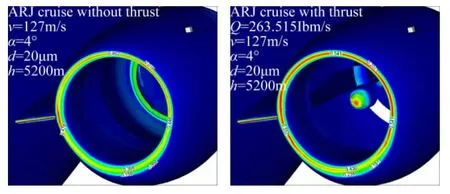
图4 飞机有/无动力表面水滴收集率云图(α=4°，d=20μm)Fig.4 Contours of collection efficiency on nacelle surface w ith＆w ithout thrust(α=4°，d=20μm)

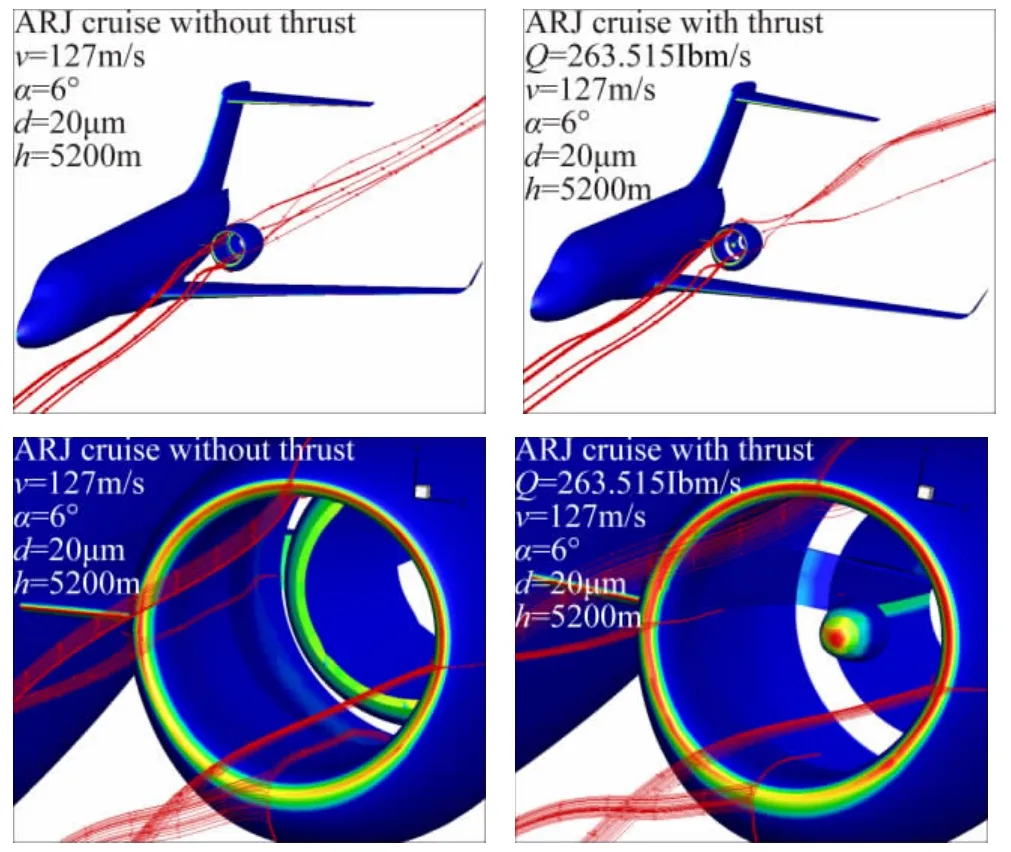
图5飞机有/无动力水滴轨迹与收集率云图(α=6°，d=20μm)Fig.5 Trajectories of droplets and contours of collection efficiency w ith＆w ithout thrust(α=6°，d=20μm)

图6给出了通气模型和动力模型在水滴直径d =10μm、攻角α=2°时，发动机短舱中心面处进气道上唇口(左图)下唇口(右图)收集率分布曲线比较。图7给出了水滴直径d=20 μm、攻角α=4°的结果。图8给出了水滴直径d=40 μm、攻角α=6°的结果。可见水滴撞击特性的变化规律为:(1)水滴收集率随水滴直径变小而减小;(2)水滴撞击范围随着水滴直径变小而减小;(3)带动力后发动机进气道唇口处水滴收集率增加，水滴撞击范围变大。

图6 短舱中心面上、下唇口处水滴收集率(α=2°，d=10μm，z=2.9m)Fig.6 Compare of collection efficiency distribution on nacelle w ith＆w ithout thrust(α=2°，d=10μm，z=2.9m)

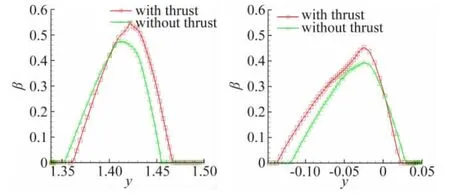
图7 短舱中心面上、下唇口处水滴收集率(α=4°，d=20μm，z=2.9m)Fig.7 Compare of collection efficiency distribution on nacelle w ith＆w ithout thrust(α=4°，d=20μm，z=2.9m)

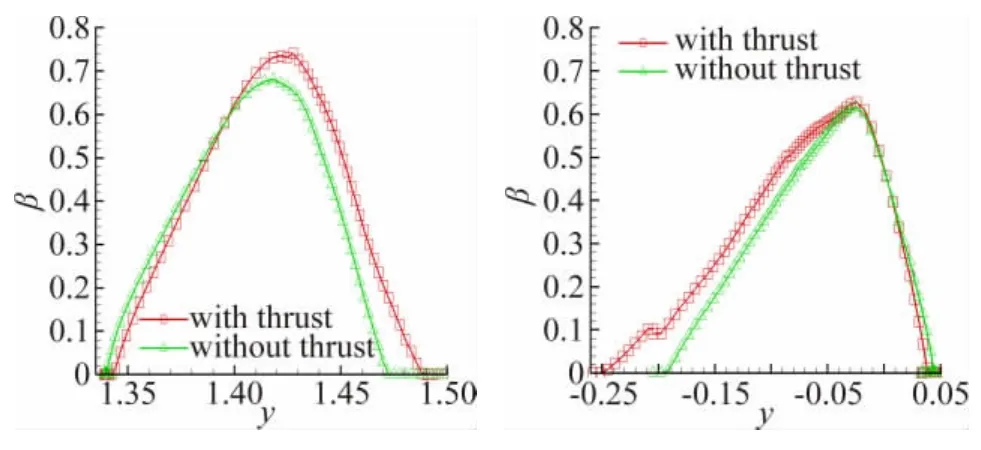
图8 短舱中心面上、下唇口处水滴收集率(α=6°，d=40μm，z=2.9m)Fig.8 Com pare of collection efficiency distribution on nacelle w ith＆w ithout thrust(α=6°，d=40μm，z=2.9m)

图9左图给出了飞机发动机通气模型和动力模型在攻角α=6°、水滴直径d=40μm时，飞机高度方向4.2m处垂尾典型剖面的水滴收集率分布比较;图9右图给出了飞机发动机通气模型和动力模型在攻角α=6°、水滴直径d=40 μm时，翼展2.9 m处平尾典型剖面的水滴收集率分布比较。计算表明:带动力模型飞机垂尾、平尾表面上的水滴收集率分布和水滴撞击范围与通气模型基本相同。因此飞机巡航构型是否带动力对垂尾、平尾的水滴撞击特性没有影响。

图10左图给出了飞机发动机通气模型和带动力模型在α=4°、d=10μm时翼展2.9m处机翼表面的水滴收集率分布比较;图10右图给出了α=6°、d= 40μm时的结果。计算表明:发动机通气模型和带动力模型的水滴收集率与水滴撞击范围在机翼上几乎完全一致，飞机巡航构型是否带动力对机翼的水滴撞击特性没有影响。

图9 垂尾、平尾典型剖面水滴收集率(α=6°，d=40μm)Fig.9 Compare of collection efficiency distribution on vertical tail and stabilizer(α=6°，d=40μm)

图10 机翼典型剖面处水滴收集率(α=4°、6°，d=10、20μm)Fig.10 Compare of collection efficiency distribution on w ing w ith＆w ithout thrust(α=4°、6°，d=10、20μm)

3 结论

本文建立了适合于飞机带动力条件下结冰过程水滴收集率计算的三维数值方法和计算程序，并对某型运输机巡航构型的水滴收集率进行了有/无动力的对比计算，得到如下结论:

1)巡航构型飞机带动力对于机翼的水滴收集率无影响，机翼部件的冰风洞试验和防除冰设计可以不考虑动力的影响;

2)巡航构型飞机带动力对于水平尾翼和垂直尾翼的水滴收集率无影响，平尾和垂尾部件防除冰设计可以不考虑动力的影响;

3)巡航构型飞机是否带动力对于发动机进气道唇口的水滴收集率影响较大，带动力后由于存在较强的气流抽吸作用，发动机进气道唇口处水滴收集率增加，水滴撞击范围变大，在进行防除冰研究和设计时需要重点关注。

［1］Cebeci T，Kefyeke F.Aircraft icing［J］.Annual Review of Fluid Mechanics，2003，35:11-21.

［2］Bragg M B，Broeren A P，Blumenthal L A.Iced-airfoil aerodynamics［J］.Progress in Aerospace Sciences，2005，41(5): 323-362.

［3］Frank T Lynch，Abdollah Khodadoust.Effects of ice accretions on aircraft aerodynamics［J］.Progress in Aerospace Sciences，2001，37(8):669-767.

［4］Yi X.Numerical computation of aircraft icing and study on icing test scaling law［D］.Mianyang:China AerodynamicsResearch and Development Center，2007.(in Chinese)易贤.飞机积冰的数值计算与积冰试验相似准则研究［D］.绵阳:中国空气动力研究与发展中心，2007.

［5］Yi X，Wang K C，Gui Y W，et al.Study on eulerian method for icing collection efficiency computation and its application［J］.Acta Aerodynamica Sinica，2010，28(5):596-601.(in Chinese)易贤，王开春，桂业伟，等.水滴撞击特性欧拉计算方法研究及应用［J］.空气动力学学报，2010，28(5):596-601

［6］Yi X，Wang K C，Zhu G L，et al.A numerical method for simulation of three dimensional ice accretion on aircraft［C］// Recent Progresses in Fluid Dynamics Research，2011:161-164.

［7］Yi X，Wang K C，Ma H L，et al.3-D numerical simulation of droplet collection efficiency in large-scale wind turbine icing［J］.Acta Aerodynamica Sinica，2013，31(6):745-751.(in Chinese)易贤，王开春，马洪林，等.大型风力机结冰过程水滴收集率三维计算［J］.空气动力学学报，2013，31(6):745-751.

［8］Yi X，Chen K，Wang K C.Application of CFD technology in wind turbine icing prober design［J］.Transactions of Nanjing University of Aeronautics＆Astronautics，2013，30(3):264-269.

［9］Yi X，Gui Y W，Zhu G L.Numerical method of a three-dimensional ice accretion model of aircraft［J］.Acta Aeronautica et Astronautica sinica，2010，31(11):2152-2158.(in Chinese)易贤，桂业伟，朱国林.飞机三维结冰模型及其数值求解方法［J］.航空学报，2010，31(11):2152-2158.

［10］Zhu G L，Kronast M.The calculation of ground effect on a car flow field using two dimensional Navier-Stokes equations［J］.Acta Aerodynamica Sinica，1993，11(1):35-40.

［11］Bragg M B，Gregorek G M，Shaw R J.An analytical approach to airfoil icing［R］.AIAA 81-0403，1981.

［12］Bourgault Y，Habashi W G，Dompierre J，et al.An eulerian approach to supercooled droplets impingement calculations［R］.AIAA 97-0176，1997.

［13］Tong X L，Luke E A.Eulerian simulations of icing collection efficiency using a singularity diffusion model［R］.AIAA 2005-1246.

［14］Patankar S V.Numerical heat transfer and fluid flow［M］.New York:Mc-Graw-Hill，1980.

［15］Ferziger J H，Peric M.Computational methods for fluid dynamics［M］.3rd Edition.Berlin:Springer-Verlag，2002.

Numerical simulation of thrust effect on droplet collection efficiency in airplane icing

Wang Kaichun，Yi Xian，Ma Honglin*，Zhao Fan
(State Key Laboratory of Aerodynamics of China Aerodynamics Research and Development Center，Mianyang 621000，China)

A three dimensional numerical method for the calculation of the droplet collection efficiency in the process of icing for an airplane with thrust is presented.The flowfield of air is computed by multiple blocks grid and SIMPLE method based on the obtained distribution，the governing equations of water phase are solved，and then the droplet collection efficiency is obtained.Both governing equations of gas and water phase are written in the form of typical transport equations，and are solved with a same finite volume method，which makes the development of numerical code easier.The droplet collection efficiency on a transport airplane cruise configuration with thrust or without thrust is computed，and the impingement characteristics of different diameter droplets are obtained，then the distribution of droplet collection efficiency on the airplane are yielded.The results show that the thrust effect of airplane on droplet collection coefficient on the wing，the vertical tail and the stabilizer is not obviously and can be ignored.However，the main effect of airplane with thrust on droplet collection coefficient occurs on the leading edge of the nacelle.The collection efficiency of airplane with thrust is higher than that without thrust on the leading edge of the nacelle，the droplet impact range of airplane with thrust is bigger than that of no thrust.

airplane;thrust effect;ice accretion;droplet collection efficiency;numerical simulation

V211.3;V321.2+29

A

10.7638/kqdlxxb-2015.0218

0258-1825(2016)03-0308-05

2015-12-21;

2016-01-01

国家自然科学基金(11172314，11472296)

王开春(1965-)，研究员，研究方向:低速空气动力学、飞机结冰、气动与水动声学计算等.E-mail:wangkaichun1965@sina.com

马洪林*(1976-)，男，副研究员，研究方向:低速空气动力学、飞机结冰的研究.E-mail:mhlhust@163.com

王开春，易贤，马洪林，等.动力对全机水滴收集率的影响计算［J］.空气动力学学报，2016，34(3):308-312.

10.7638/kqdlxxb-2015.0218 Wang K C，Yi X，Ma H L，et al.Numerical simulation of thrust effect on droplet collection efficiency in airplane icing［J］.Acta Aerodynamica Sinica，2016，34(3):308-312.