星载GNSS-R天线波束指向算法研究

杜璞玉，周　勃，秦　瑾

(上海航天电子技术研究所，上海 201109)



星载GNSS-R天线波束指向算法研究

杜璞玉，周勃，秦瑾

(上海航天电子技术研究所，上海 201109)

摘要利用GNSS反射信号进行遥感探测，已成为国内外遥感和导航技术领域研究热点之一。星载GNSS-R遥感探测的几何关系和相控阵天线的波束指向算法更加复杂，对算法精度和实时性的要求更高。基于星载GNSS-R应用，给出了星载GNSS-R相控阵天线波束指向算法，对比了2种计算波束指向角的方法，并通过Matlab与STK联合仿真分析说明，使用探测仪速度和位置矢量进行波束角计算的方法，具有更高的精度，且实时性满足要求，适用于星载应用。

关键词星载GNSS-R；波束指向算法；波束角计算；速度位置矢量法

Research on Spaceborne GNSS-R Antenna Beam Pointing

DU Pu-yu,ZHOU Bo,QIN Jin

(ShanghaiAerospaceElectronicTechnologyInstitute,Shanghai201109,China)

AbstractThe application of Global Navigation Satellite Systems - Reflectometry(GNSS-R)to remote sensing and exploration is one of the hotspots in the field of remote sensing and navigation technologies.The geometrical relation of spaceborne GNSS-R remote sensing and exploration and beam pointing algorithm of phased array antenna are more complicate,with higher requirements of accuracy and realtime performance.Based on spaceborne GNSS-R application,this paper puts forward spaceborne GNSS-R phased array antenna beam pointing algorithm.The two methods of computing beam pointing angle are compared.The Matlab and STK combined simulation analysis shows that the method using position and velocity vectors for beam angle computing has higher accuracy and realtime performance,and is suitable for spaceborne missions.

Key wordsspaceborne GNSS-R;beam pointing algorithm;pointing angle calculation;PV vector method

0引言

GNSS-R(Global Navigation Satellite System-Reflection)技术是通过微波遥感装置同时接收并处理导航卫星直射信号以及海面的反射信号，实现海洋特征要素提取或目标探测的技术[1,2]，是国内外遥感领域研究热点之一。GNSS-R探测仪对接收到的反射信号进行时延、多普勒补偿，然后与直射信号做互相关，得到所谓的DDM(Delay-Doppler Maps)，并由此反演海面状态参数[3]。

由于采用干涉式互相关结构[4]，GNSS-R探测仪需实时指向选定的导航卫星和其对应镜面反射点(以下简称镜点)。工程中，采用多波束上视/下视相控阵天线，上视天线指向导航卫星，下视天线指向其对应的镜点[5,6]，在多波束工作模式下，相控阵天线同时指向多对目标。

有关学者对传统意义下的卫星指向问题进行了研究，并给出了天线指向计算模型[7-10]，而星载GNSS-R遥感探测的波束指向算法对精度和实时性的要求更高。本文基于星载GNSS-R应用，给出了星载GNSS-R相控阵天线波束指向算法在工程实现中的具体流程，详细介绍了使用GNSS-R探测仪的位置和速度矢量计算波束指向角的方法，该算法具有精度高、实时性好的特点，尤其适用于星载应用。

1星载GNSS-R天线波束指向算法

除相控阵天线外，GNSS-R探测仪还配有上视宽波束天线用于寻找当前时段的可见的导航卫星，接收机计算各卫星位置以及相对于探测仪的方位、俯仰角，根据选星策略选择最符合应用要求的卫星。然后计算所选导航卫星对应的镜面反射点位置，计算天线波束指向角，调度上/下视相控阵天线波束指向导航卫星和镜点，完成直射信号和反射信号的接收。波束指向算法流程如图1所示。

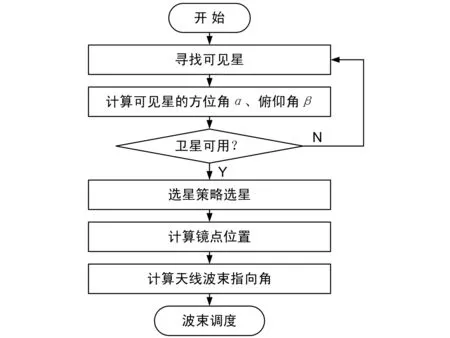
图1　波束指向算法流程

2波束指向角计算原理

星载GNSS-R应用中，已知导航卫星、GNSS-R探测仪在WGS-84坐标系下的位置及速度矢量，由此可以根据镜点预测算法计算出镜点坐标。但是最终的天线波束指向角需在天线本体坐标系下度量，因此有必要将探测仪相对于导航卫星和镜点的指向矢量转换到天线本体坐标系下，涉及到的坐标转换步骤如图2所示。

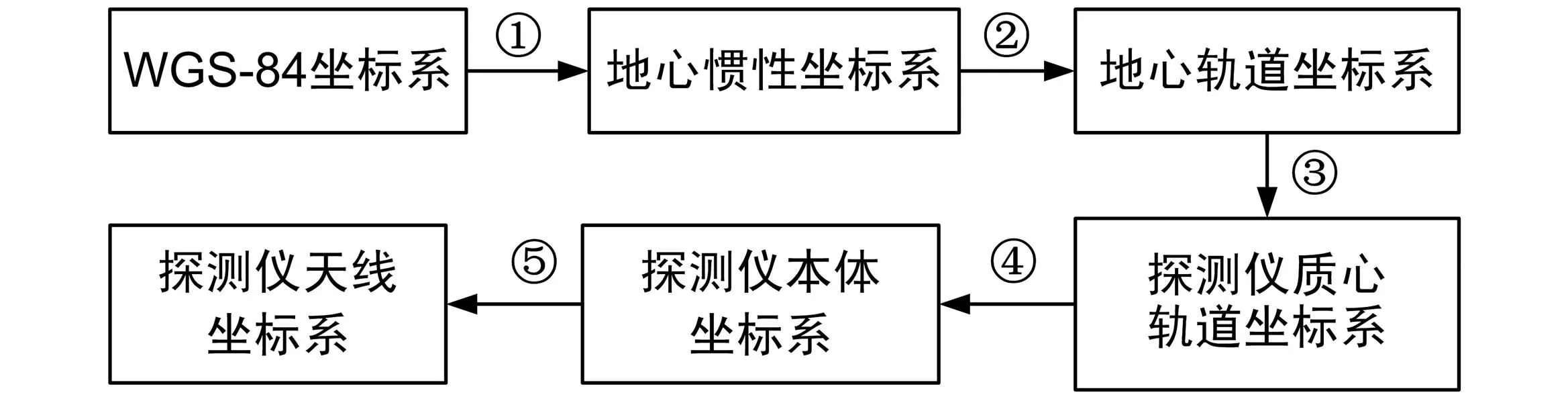
图2　波束指向计算坐标转换流程

有2种方法可以完成上述坐标转换：使用探测仪轨道根数(以下简称轨道根数法)和使用探测仪的位置和速度矢量(以下简称PV矢量法)，2种方法所需的输入参数不同。本文将对2种方法进行分别介绍，并通过仿真对比说明使用探测仪位置和速度矢量的方法更适用于星载GNSS-R应用。

2.1使用轨道根数法进行坐标转换

在图2的转换过程中，步骤①与地球的自身运动有关；步骤②和步骤③需要用到GNSS-R探测仪的轨道根数，如式(1)和式(2)所示；步骤④与探测仪的姿态有关；步骤⑤由天线在探测仪上的安装位置及方式决定。

① J2000.0地心惯性坐标系OXiYiZi到探测仪地心轨道坐标系OXoYoZo

(1)

式中，ω为探测仪所在低轨卫星的近地点幅角；i为轨道倾角；Ω为升交点赤经。

② 探测仪地心轨道坐标系OXoYoZo到探测仪质心轨道坐标系OXmYmZm

(2)

式中，v为真近点角；下标(.)表示任一点；下标(LEO)表示探测仪。

2.2使用PV矢量法进行坐标转换

该方法的基本思想是：根据质心轨道坐标系的定义，直接利用在惯性坐标系下卫星的绝对速度和绝对位置矢量求解质心轨道坐标系的坐标轴，然后再将测量值分别对各坐标轴进行投影，即可得到质心轨道坐标系下的测量值[11]。

具体过程为：令r、v和δr分别为惯性系下探测仪的绝对位置、绝对速度和相对位置矢量，则质心轨道坐标系下的目标间的相对位置矢量δro=(xoyozo)T可用下式计算：

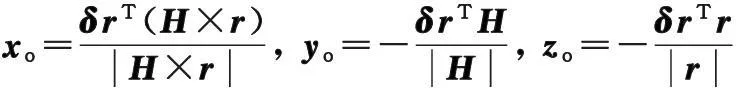
(3)

式中，H=r×v。

注意到，式(3)中的矢量都定义在惯性坐标系下，因此需将WGS-84系下的已知矢量先转化到惯性坐标系中，这一过程不需要探测仪轨道根数。

3算法仿真

为验证算法的正确性及性能，使用STK软件建立场景，与Matlab进行联合仿真。考虑到探测仪质心轨道坐标系到探测仪本体坐标系，再到天线本体坐标系的转换，只与探测仪的摆放位置和天线的安装方式有关，不失一般性地，假设上述3个坐标系重合，仿真过程中，坐标转换只进行到探测仪质心轨道坐标系。为简化仿真条件，STK场景中，只验证了可访问时间段内探测仪对一颗可见导航卫星及其镜点的指向，对多波束的情形，按照此方法增加对象即可。仿真参数如表1所示。

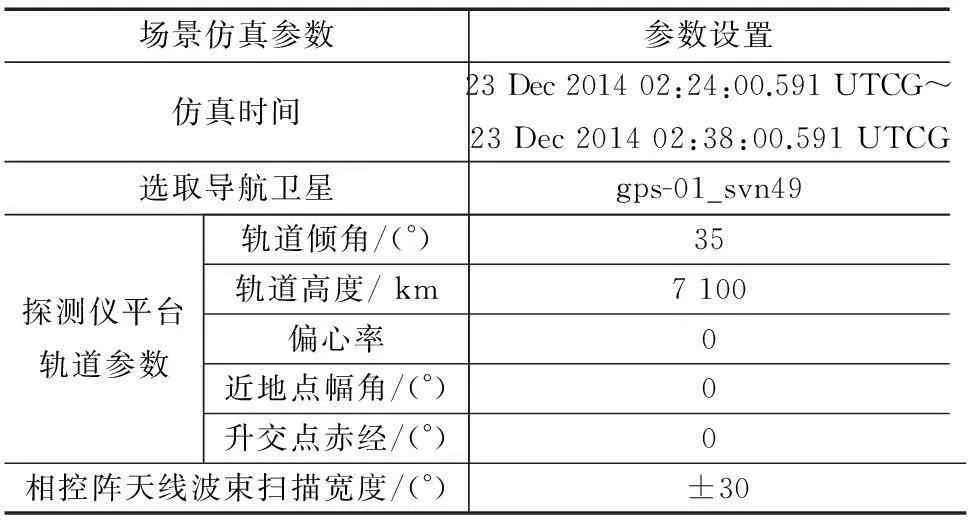
表1　仿真参数

Matlab程序以STK软件生成的“Fixed Position Velocity”、“Classical Orbit Elements”报告中提供的位置矢量、速度矢量和探测仪平台轨道根数为输入。镜点由场景中的对象“ship”表示，轨迹由Matlab在计算完成后赋值。

以STK软件生成的“AER”访问报告作为参考，与程序计算结果进行对比，以验证算法正确性。

3.1轨道根数法算法仿真

由“Classical Orbit Elements”报告提供的轨道根数，解算出导航卫星、探测仪平台和镜点在惯性系下的坐标，再转换到探测仪质心轨道坐标系，计算指向角。仿真结果及误差分析如图3和图4所示。

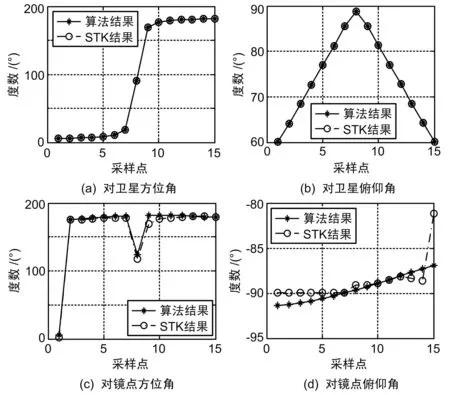
图3　轨道根数法仿真结果

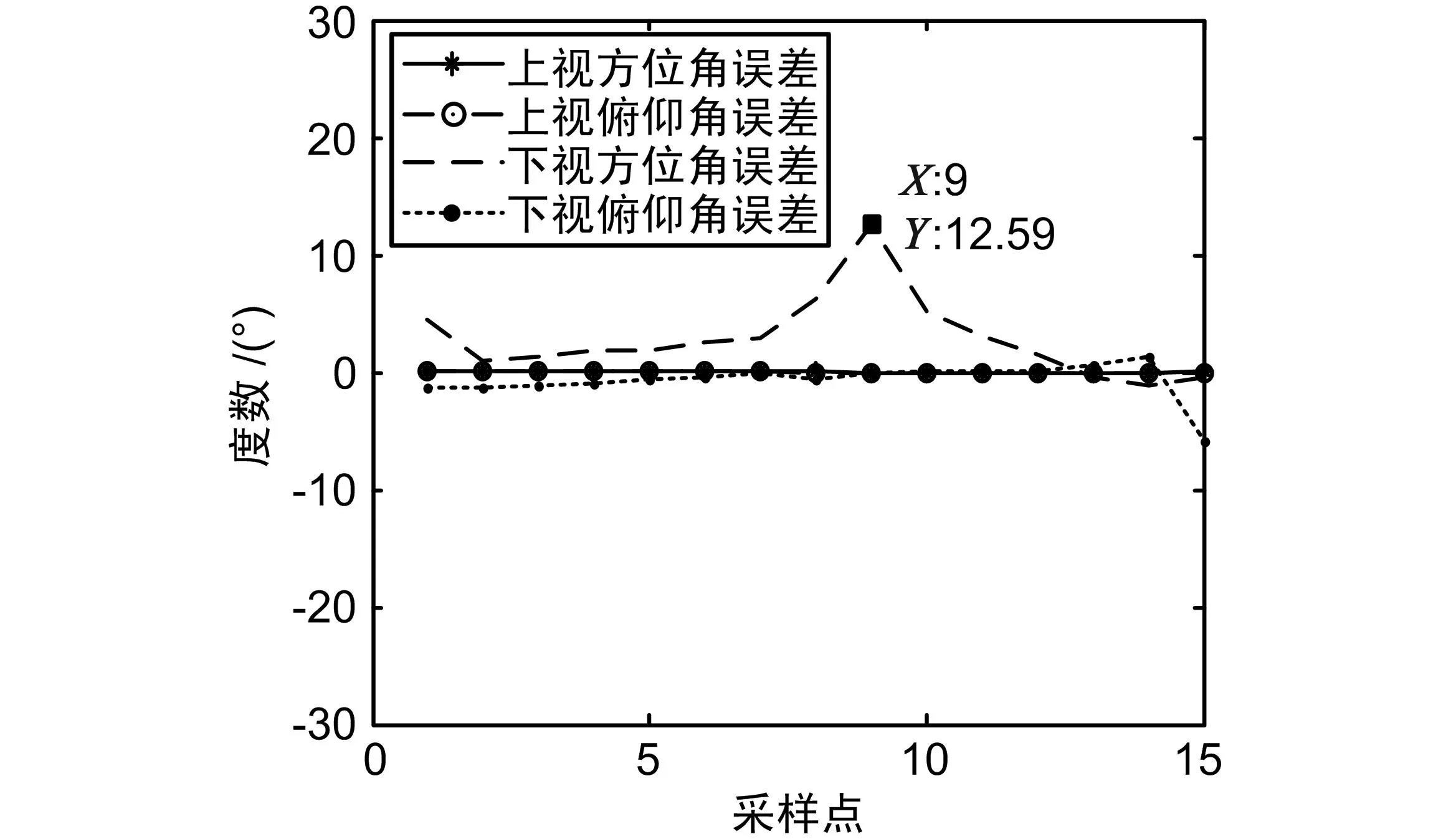
图4　误差分析

3.2PV矢量法算法仿真

由“Fixed Position Velocity”报告得到导航卫星和探测仪平台在WGS-84坐标系下的位置和速度矢量，计算出镜点位置。先将坐标转换到惯性系下，再通过式(3)直接求得探测仪质心轨道系下指向向量的坐标，计算指向角。仿真结果和误差分析如图5和图6所示。

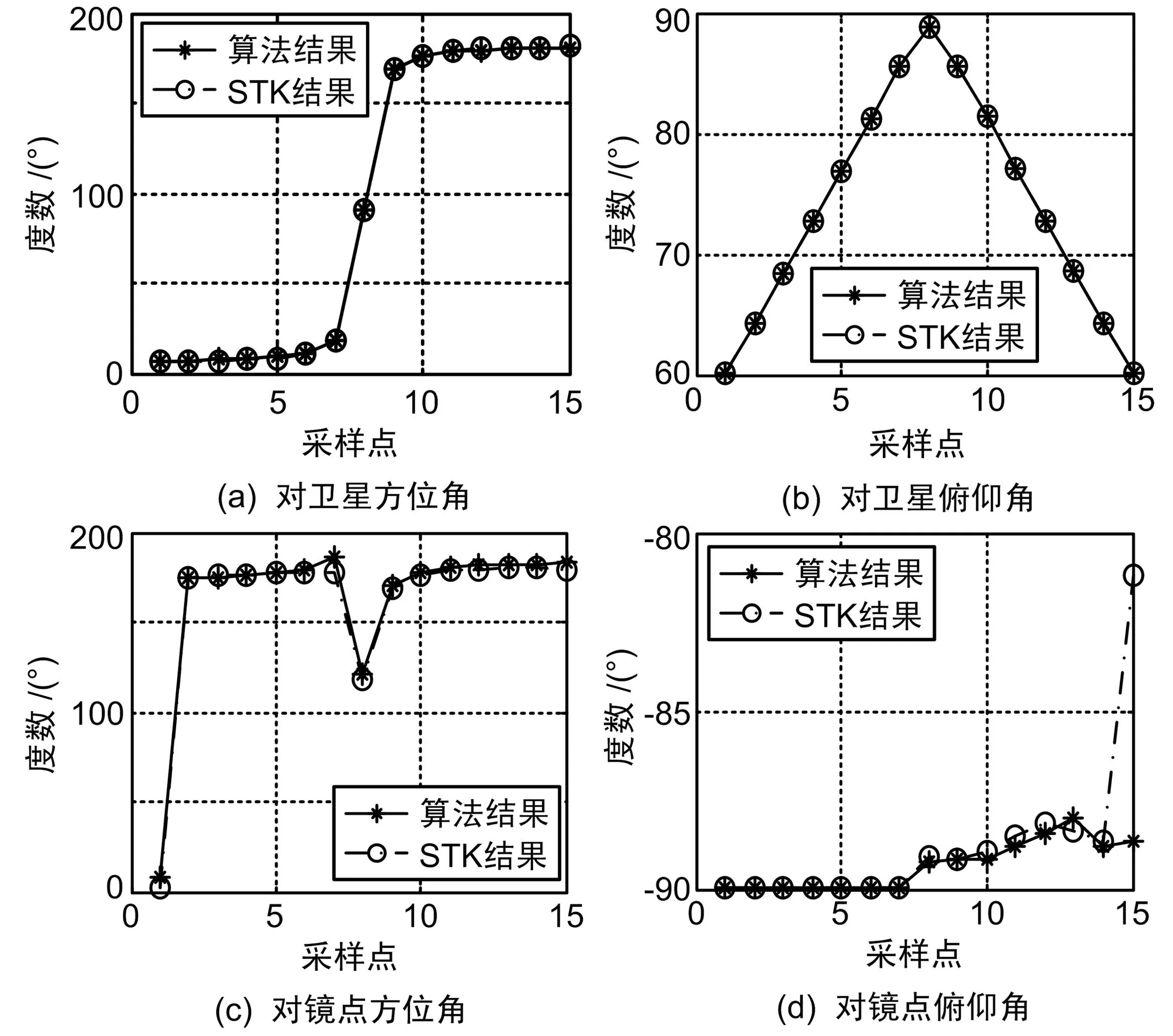
图5　PV矢量法仿真结果

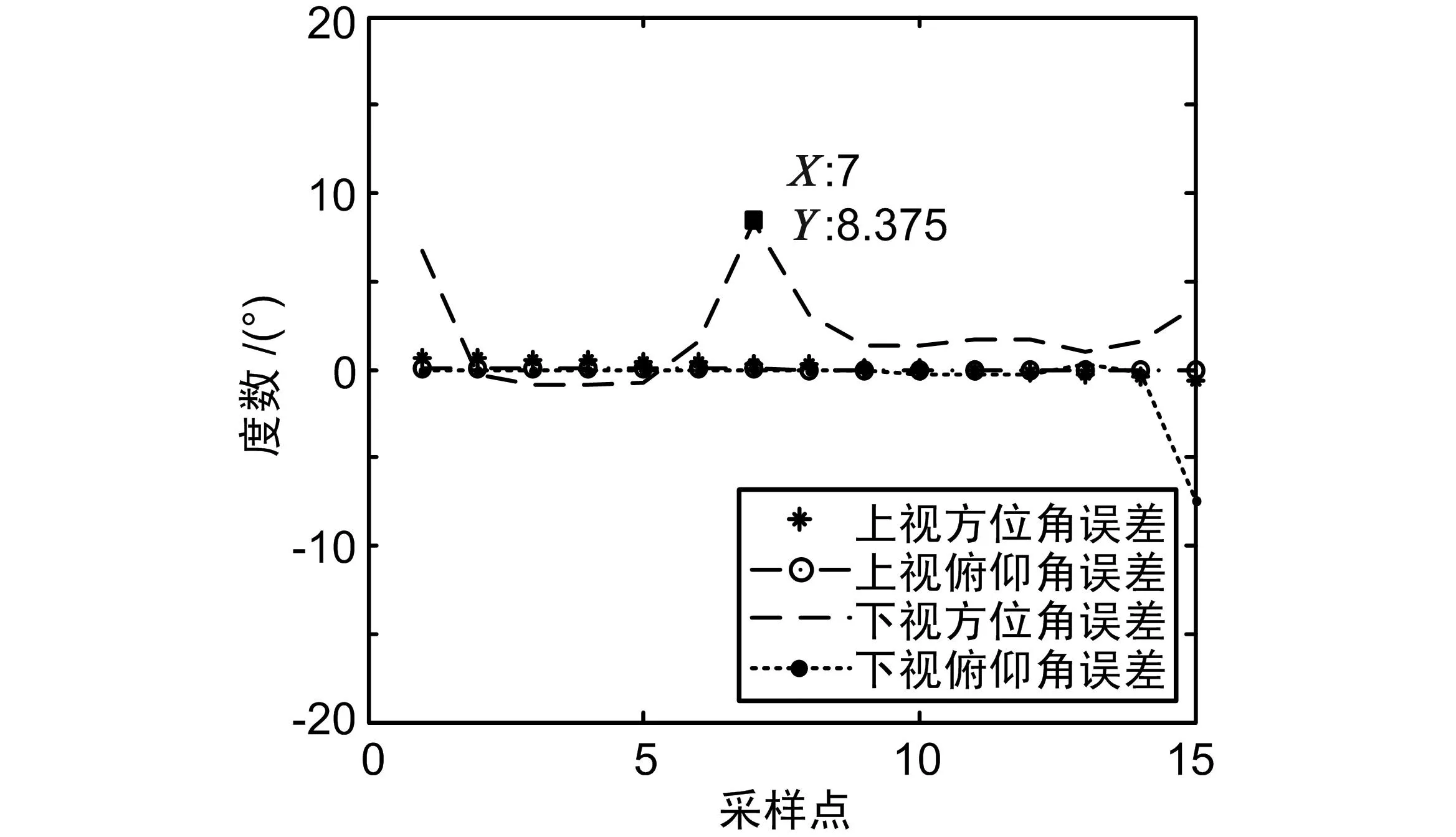
图6　误差分析

3.3结果分析

从仿真结果可以得出以下结论：

① 对上视导航卫星的指向，2种算法都有较好的表现。

② 2种算法对镜点的指向误差都明显大于对导航卫星的指向误差。原因为：镜点的轨迹是通过镜点预测算法计算得到再赋值给STK中的对象的，镜点轨迹对应的时刻与导航卫星和探测仪轨迹对应的时刻存在偏差，由此引入误差。

③ PV矢量法性能明显优于轨道根数法。2种算法的最大误差和平均误差如表2所示。考虑到较大的误差值主要来源于对镜点的指向，因此实际应用中误差将会更小。

表2　算法误差分析

从星载应用角度考虑，由于卫星运动过程受各种外力作用，卫星的运动通常为有摄运动，且相应的轨道为变化椭圆，卫星的轨道根数将随时间缓慢变化，导致指向精度降低。相比之下，探测仪的位置和速度信息可以实时获得，保证指向精度。综合看来，使用探测仪位置和速度矢量进行波束指向计算具有较高的精度，且更适用于星载应用。

4实时性分析

计算用户星波束指向的输入条件之一是当前的时刻，由于卫星一直处于高速运动状态，而计算指向角需要一定的时间，最终波束指向与当前时刻卫星位置存在偏差，且计算指向所花的时间越长，指向误差越大。因此，有必要对算法实时性进行分析。

以PV矢量法为例，假设计算波束指向的起始时刻为t0，以1 min 为时间间隔计算波束指向角，再令起始时刻为t0+Δt，以1 min为时间间隔计算波束指向角，2次计算结果的差值即计算延时为Δt引起的误差。取Δt为1 s，仿真结果如图7所示。

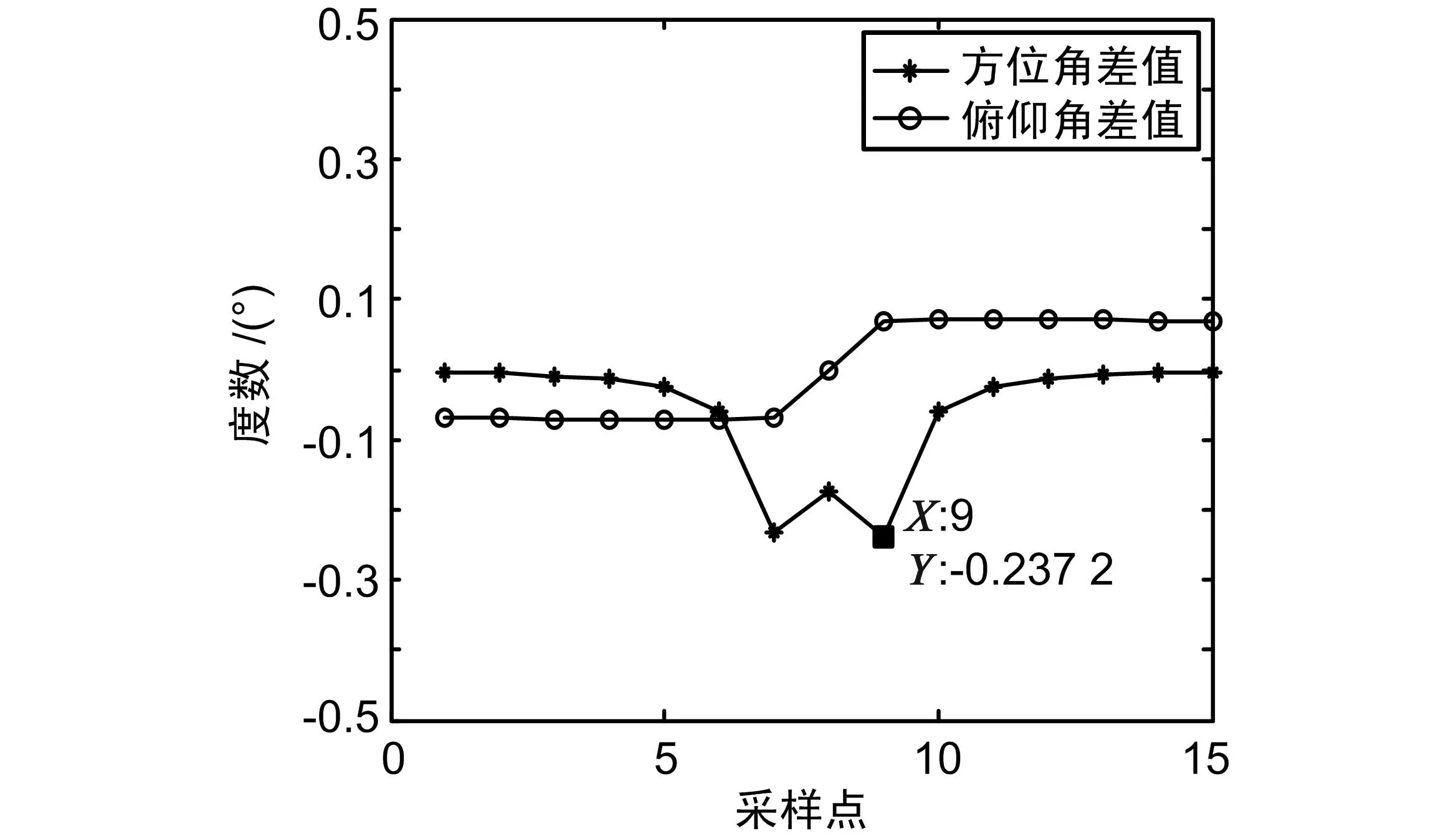
图7　实时性分析

可以看出，1 s计算时延引起的误差最大为0.237 2°，考虑到实际工程应用中，波束更新周期只有几十ms，由此带来的误差几乎可以忽略。因此算法的实时性满足要求。

5结束语

由于导航卫星和探测仪的高速运动，星载GNSS-R技术对相控阵天线波束指向算法的精度和实时性提出了较高的要求。本文首先给出了星载GNSS-R相控阵天线波束指向算法流程，着重介绍了2种计算波束指向角的方法。仿真结果表明，虽然对镜点的指向结果存在较大的误差，但考虑到仿真中对镜点指向计算的特殊性，以及对导航卫星指向结果的良好表现，可以认为文中所给出的2种算法的正确性得以验证。其中，使用探测仪位置和速度矢量进行坐标转换以求解波束指向角的方法具有更高的精度，且在ms级的波束更新周期下产生的计算延迟误差几乎可以忽略，实时性满足星载应用要求。

参考文献

[1]李伟强,杨东凯,李明里,等.面向遥感的GNSS反射信号接收处理系统及实验[J].武汉大学学报(信息科学版),2011(10):1 204-1 208.

[2]张益强.基于GNSS 反射信号的海洋微波遥感技术[D].北京:北京航空航天大学,2008.

[3]PARK H,VALENCIA E,CAMPS A,et al.Delay Tracking in Spaceborne GNSS-R Ocean Altimetry[J].Geosicence and Remote Sensing Letters,2012,99:57-61.

[5]RIUS A,CARDELLACH E,MARTN-NEIRA M.Altimetric Analysis of the Sea-Surface GPS-Reflected Signals[J].IEEE T.Geoscience and Remote Sensing,2010,48:2 119-2 127.

[6]PARK J T.JOHNSON J,MAJUREC N,et al.Airborne L-Band Radio Frequency Interference Observations From the SMAPVEX08 Campaign and Associated Flights[J].IEEE T.Geoscience and Remote Sensing,2011,49:3 359-3 370.

[7]谌浪.星载相控阵天线波束指向及控制算法研究及控制算法研究[D].上海:上海航天技术研究院,2014.

[8]高照照,杨慧.卫星锐波束天线指向算法及仿真[J].中国空间科学技术,2008(2):60-65.

[9]靖法.卫星点波束天线指向策略及控制研究[D].哈尔滨:哈尔滨工业大学,2012.

[10]李于衡,孙恩昌,易克初.中继卫星与用户星双向跟踪关系及策略[J].西安:西安电子科技大学学报,2007,34(1):6-10.

[11]刘洋,易东云,王正明.地心惯性坐标系到质心轨道坐标系的坐标转换方法[J].航天控制,2007(2):4-8.

杜璞玉男，(1991—)，硕士研究生。主要研究方向：GNSS-R算法研究与总体设计。

周勃男，(1979—)，硕士研究生。主要研究方向：GNSS-R总体设计。

作者简介

收稿日期：2015-10-09

中图分类号TN957.51

文献标识码A

文章编号1003-3106(2016)03-0045-04

doi:10.3969/j.issn.1003-3106.2016.03.13

引用格式：杜璞玉,周勃,秦瑾.星载GNSS-R天线波束指向算法研究[J].无线电工程,2016,46(3):45-48.