一种组合模型状态监测方法研究
李小珉 张 波 尹 明
(海军工程大学电子工程学院 武汉 430033)
一种组合模型状态监测方法研究
李小珉张波尹明
(海军工程大学电子工程学院武汉430033)
摘要目前在状态监测过程中分类器的类型和参数的选择对状态监测率有很大影响,而且任何单一模型使用过程中都会出现不理想的方面,提出一种参数优化与组合模型相结合的新方法。结合支持向量机(SVM)能够处理分类问题和隐马尔科夫模型(HMM)适合处理连续信号的特点,同时考虑到SVM的参数设置对结果影响较大,采用粒子群算法(PSO)对SVM进行优化,最终形成组合模型HMM-PSOSVM。通过实验验证了其具有良好的模拟电路早期状态监测能力。
关键词特征提取; 状态监测; 组合模型
A State Monitoring Method of Combination Model
LI XiaominZHANG BoYIN Ming
(School of Electrical Engineering, Naval University of Engineering, Wuhan430033)
AbstractSelecting the suitable type and parameters of the classifier has a great influence on state monitoring rate in the state monitoring process currently, and any single model will appear not ideal aspect in using process, a novel method combined with a parameter optimization and combination model is put forward. Because the Support Vector Machine(SVM) can deal with classification problems and Hidden Markov Model(HMM) is suitable for the characteristics of processing continuous signal, at the same time, taking into account the parameter of SVM has great impact on the results, using the Particle Swarm Optimization algorithm(PSO) to optimize SVM, and ultimately forming the HMM-PSOSVM combination model. The experimental results show that the new method has excellent capability of monitoring incipient fault.
Key Wordsfeature extraction, state monitoring, combination model
Class NumberTP277
1引言
故障预测与健康管理(PHM),代表了一种方法的转变,它的重点是利用先进的传感器的集成,并借助各种智能算法对不同部位采集的数据信息进行分析,评定出系统的状态情况,然后综合各种保障资源对故障进行定位、隔离和预测[1]。这种技术的提出不仅可以根据系统当前的健康状态和资源实现故障的排除,而且可以根据系统健康状态的评估实现故障的预测,在故障发生之前进行维护保养,节省寿命周期费用[2]。
状态监测是PHM技术的基础和重点,通过状态监测实时掌握系统状态情况,在此基础上评估系统健康状况,进而实现故障的诊断和预测。电子系统的状态监测是利用传感器采集状态数据信息,通过智能算法和模型评估系统当前状态,此方法标志着传统故障诊断方式向智能故障预测方式的转变。基于PHM技术的电子系统状态监测主要包括特征提取、状态识别与预测等模块[3],其方法体系如图1所示。

图1 状态监测方法体系
在状态监测过程中分类器及其参数的选择至关重要,直接影响着监测和识别结果,而目前为止任何单一模型使用过程中都会出现不理想的方面,本文将针对这一问题提出一种参数优化与组合模型相结合的优化方法,并通过仿真实验进行验证。
2常用状态监测器及其优化
2.1隐马尔科夫模型HMM
隐马尔科夫模型(HMM)是一种通过概率统计方法对事件与信号之间的随机过程进行描述的双重随机概率模型。一重过程是使用Markov链对状态的概率转移进行描述,另一重是描述状态与观察值之间的关系。由于模型状态不是直观可见的,只能通过状态转移的随机过程来评估事件的状态[4]。
HMM可以定义为五个基本参数集合:λ=(S,V,π,A,B)。
1)S为有限状态集合,S=(S1,S2,…,SN),N表示状态个数,状态之间相互关联,可以视情况相互转换,如果模型在t时刻的状态是Si,那么Si∈(S1,S2,…,SN);
2)V为有限观察符号集合,V=(V1,V2,…,VM),M表示对应状态下的观测值的个数,若模型在t时刻的观测值是Vi,那么Vi∈(V1,V2,…,VM);
3)π是初始化概率向量,π=(π1,π2,…,πN),πi=p(qi=si),i=1,2,…,N,π指的是初始阶段第一状态选取选择状态集合中某个状态时的概率,而且∑πi=1;
4)A是状态转移矩阵,A={aij},个别情况下某状态可以转变为其他状态,aij是由当前状态i转变为其他状态j时的概率;

5)B是观察概率矩阵,bij表示当处于状态xi时出现观测序列xj的概率。所以HMM可以表示为λ=(S,V,π,A,B),或者简化表示为λ=(π,A,B),其中π、A表示模型中状态序列输出,B表示是模型的观察值序列输出。
2.2非线性支持向量机SVM
支持向量机(SVM)是上个世纪90年代中期Vapnik和合作者在统计学理论基础上,建立的一套针对小样本和分类问题,采用结构风险最小化准则(SRM)的基于核的新型机器学习法[5]。
设输入向量x经核函数从输入空间Rn映射到高维空间中:
因为在输入空间映射到高维空间的非线性过程只需要应用到内积过程(φ(x1)·φ(x2)),不用考虑φ的具体形式,所以这里定义核函数K(x,y),且令K(x,y)=φ(x)·φ(y)。在非线性情况下,寻找最优超平面时,只需要运用合适的核函数代替线性支持向量机分类超平面条件中的点积,即可得到非线性支持向量机的拉格朗日函数的对偶形式:
(1)
求解可得非线性高维空间的决策函数:
(2)
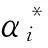
2.3基于粒子群优化算法(PSO)的SVM
粒子群算法(PSO)是由Kennedy和Eberhart等于1995年开发的一种智能优化算法,其基本思想来源于对鸟群简化社会模型的研究及行为模型。粒子群算法将粒子群中的个体都看做是没有体积和质量的微粒,通过粒子对环境的学习和适应,利用个体和群体之间飞行经验的综合飞行结果来调整粒子的飞行速度及所处的位置。它是一种基于群体智能的演化计算方法,通过群体中粒子间的合作与竞争产生的群体智能指导优化搜索。其特有的记忆使其可以动态跟踪当前的搜索情况调整其搜索策略,是一种更高效的并行搜索算法[6]。PSO具有原理简单、收敛速度快等优点,需要调节的参数较少[7]。下面对PSO中的相关参数进行简单分析。
1) 惯性因子w
w能反映出前一时刻的速度对当前速度的影响,能直接左右算法全局以及局部搜索能力。w值越大,算法全局搜索能力就越强;反之算法的局部搜索能力越强。适合的惯性因子能较好地平衡算法的局部搜索能力和全局搜索能力,而且不同的情况下惯性因子的取值是不一样的,所以要根据实际情况,选择最优惯性参数w。
为了使PSO取得更好的搜索能力,首先在前期需要较强的全局搜索能力,这时惯性因子的取值要偏大,在后期就需要对局部区域进行高精度搜索(局部搜索能力),此时惯性因子的取值要尽量小一点。所以惯性因子w在取值时,刚开始取值要大,随后逐渐减小,因此惯性因子w是随着时间的增大而逐渐递减的变化值。
2) 群体规模m
种群规模越大,包含的粒子越多,此时参与搜索的粒子也就越多,此时的粒子群算法具有较好的搜索能力,但计算时间会增加。根据文献[8]实验证明当种群中粒子数量增大到一定后,该算法的搜索能力就没有明显的变化,大多数文献在实验时一般将粒子群的种群数量取为50,当研究问题较为复杂时可以适当增加粒子的数量。
3) 加速因子c1和c2
加速因子c1和c2的作用是分别用来调节粒子飞向个体最优方向和群体最优方向的概率[9],当加速因子取值较小时,粒子飞向目标区域的概率较小;当加速因子取值增大时,粒子飞向目标区域的概率增加,但是当取值过大就有可能直接飞越而过。
当c1取零而c2不为零时,粒子没有自身的认知能力[10],该状态下的粒子能够到达新的搜索空间,但是如果粒子数量较多,问题比较复杂时,容易仅局限于局部最优。
当c2取零而c1不为零时,粒子间信息互不共享,“只有认知”模型[10],该状态下的粒子之间没有相互联系,各粒子的运动相互独立,该情况下的算法很难取得最优解。
当c1和c2同时取零时,粒子既没有“认知”能力,相互间也没有信息共享,所以该状态下的粒子会按照原来的速度飞行,直到飞到边界,该情况下的算法只能搜索很小的区域。
4) 最大速度Vmax
粒子的最大速度Vmax影响着粒子搜索空间的能力,当Vmax取值加大时,粒子的搜索能力变强,但是可能出现粒子越过最优搜索空间的问题;当Vmax取值较小时,粒子局部搜索能力强,但可能出现达不到空间最优区域,而仅局限于局部最优。
支持向量机中对核函数的选择没有较好的标准和方法,虽然已经提出很多种理论方法通过选择期望风险最小的参数作为最优参数,但是在实际使用中选择最优参数范围比较难以把握,而且精度比较低。粒子群算法通过群体中各微粒相互协调与合作来寻找最优解,而且该方法需要调节的参数比较少,易于实现。下面将通过PSO算法对SVM进行优化,以RBF作为核函数,通过对惩罚系数C、核参数σ的优化得到最优SVM模型[11]。具体过程如下:
1) 确定搜索空间
由于σ过大时会出现“欠学习”现象,过小时则会出现“过学习”现象,而且根据高斯核函数的定义可以知道σ的值与‖x-y‖2的值有关,但是在应用中σ的值比训练样本最小间距小的话会出现σ的值无限接近于零的现象,而σ的值大于样本最大间距就会出现σ的值接近于无穷大的现象,所以可以设置σ的值的搜索范围:{min(‖x-y‖2×10-2),max(‖x-y‖2×10-2)},并且可以逐步缩小搜索空间来提高效果。
惩罚因子C主要受到Lagrange乘子α的影响,为了取得适当的C值进行训练可以进行如下方法:当C>C1时可以取适当的值进行训练,求得Lagrange乘子α;当C≤C1时则需要重新取C的值,直到C1远小于C时为止,所以可以定义惩罚因子C的搜索空间为(0,C1)。
2) 初始化
对PSO算法中的每个微粒随机定义一组{C,σ},粒子会在空间中与状态相互对应的节点间相互运动,此时微粒在运动中可以根据目标函数的信息进行搜索。
POS-SVM实现步骤[12]是:
1) 初始化粒子群算法调节参数(粒子群规模m,惯性因子W,粒子自身加速系数C1,全局加速系数C2,粒子的初始位置和速度等);
2) 计算各微粒的适应值;
3) 将各微粒适应值与最佳位置Pi比较,重新选择其中的最优值作为最新最佳位置;
4) 将所有微粒最佳位置与全局最佳位置Pg比较,若优于Pg则取其为新的全局最佳位置,否则Pg保持不变;
5) 计算惯性因子W,求得新的位置和速度;
6) 若满足终止条件则停止搜索,此时的输出值就是SVM的最优参数,若不满足条件则返回第二步继续搜索。
3HMM-PSOSVM组合模型
根据HMM和SVM分别作为状态监测器的原理和方法,通过实验可以得出HMM在处理连续信号方面表现理想,能够很好地反映样本间的相似度,而SVM在处理分类问题方面表现理想,能够很好地体现不同样本间的差异。所以将HMM和粒子群优化的SVM模型的优点结合起来构成组合模型[13],实现优势互补的组合模型能很好地识别电子系统的不同状态,组合模型结构设计如图2所示。
该组合模型共分成四个层次:输入层、隐马尔科夫训练和识别模块、支持向量机训练和识别模块、输出层。输入模块中通过传感器实时监测电路系统中的状态,提取出电子系统的状态特征,并将特征信号通过预处理,去除原始特征中的冗余性、高维性,预处理后的特征能够更好地反应出电路的状态信息。隐马尔科夫训练和识别模块中,根据电路不同情况MC分析中容差的设置,不同的HMM模型输出的最大似然值可能会出现相似现象,这时不能仅仅通过最大似然值的大小来判断电路系统的状态。所以可以引入SVM的训练和识别模块,利用支持向量机较好的分类能力来解决模式识别中出现误判的问题,同时HMM训练和识别模块中对连续信号的处理能力也可以弥补支持向量机在处理分类问题中因不进行时序信号方面特征的处理而出现误判的不足。最后通过输出模块将最终的结果输出反馈出来。

图2 HMM-PSOSVM状态监测模型
组合模型识别问题分为隐马尔科夫模型和支持向量机两个层次,首先将测试样本经过预处理后提取出含有丰富状态信息的数据特征,然后将处理后的测试特征序列输入到HMM模型的分类层中,通过分析样本间的相似度,排除P(V|λi)较小的样本,将剩下的测试样本与设定的阈值进行比较,如果经过隐马尔科夫模型训练后的测试样本的最大似然值大于设定的阈值则直接输出分类效果,如果小于设定的阈值则将其进一步输入到支持向量机的识别层次;利用SVM解决二分类问题的优势进行分类并输出结果,这样可以很好地减少计算量,并能有针对性地提高分类识别率,这样的组合模型在保证分类效率的同时也节约了时间。
4仿真实验
具体实验如下:
1) 电路选择,采用如图3所示的标准二阶高通滤波器作为实验电路:

图3 二阶高通滤波器
设置R1=6.2kΩ,R2=6.2Ω,R3=6.2kΩ,R4=1.6Ω,R5=5.1kΩ,R6=10kΩ,C1=5nF,C2=5nF,激励源设为2V,幅角为0°,电路输出点作为测试点,实验时选择R1、R2、R3、R4、C1、C2作为故障元件,设置电路中电阻的容差为±10%,电容的容差范围为±5%。故障分为增大和减少两类(电阻和电容向上超出容差范围和向下超出容差范围两类),再加上正常态则电路共有13类状态;
2) 将通过MC分析提取出的100组数据采用非线性特征提取方法进行预处理和特征提取;
3) 设置隐马尔科夫模型的参数初始值,并将处理好的各状态的特征向量输入到HMM模型中进行训练,建立不同状态的HMM模型;
4) 建立支持向量机二分类器,由于该电路有12种故障状态外加正常状态共有13种状态,所以采用一对一策略建立二分类器;
5) 参数优化。采用PSO对采用高斯核函数的SVM的参数进行优化;
6) 状态识别。将测试数据输入到训练好的13个HMM模型,通过前向—后向算法计算对应的最大似然值,将计算出来的似然值与设定的阈值(当最小似然值与最小值的差值,本次实验时取值为2进行对比,若满足条件则直接输出识别结果,如果不满足条件则输入到SVM分类层中进行二次状态识别,并输出最终状态类别。
实验结果分析:
从表1所示的结果中可以看出: 1) 经过粒子群参数优化后的支持向量机分类能力有所提升,所以参数优化方法在提升模型分类能力的同时也能提升系统整体的状态监测能力; 2) 隐马尔科夫模型和粒子群参数优化的支持向量机组成组合模型在状态识别率方面表现良好,比采用单一模型做状态监测器时的识别率都要高,说明该组合模型既具有隐马尔科夫模型在处理连续信号问题方面的优势,又有支持向量机在处理分类问题方面的优点,实现了两模型优势上的互补。

表1 不同状态监测器时的识别率
5结语
由于HMM能很好地体现样本间的相似度,比较适合处理连续信号,而SVM能够很好地反映不同样本间的差异,在处理分类问题方便表现突出,所以根据这两种模型的优点提出一种新模型HMM-SVM,这种组合模型在兼顾两者优点的同时也能解决HMM处理似然值相似时分类能力不强,以及支持向量机在处理分类问题时因时序性问题而分类效果不佳的缺点。另一方面由于SVM在参数选择方面方法和思想不够统一,没有较好的参数优化方法,所以提出一种基于PSO优化的SVM参数优化方法,通过实验验证优化后的SVM在分类问题方面比不采用参数优化方法时的分类效果好。基于以上结论,本文提出了基于HMM-PSOSVM的组合模型,通过验证该方法的状态识别率有较大提升。
参 考 文 献
[1] 张宝珍.国外综合诊断,预测与健康管理技术的发展及应用[J].计算机测量与控制,2008,16(5):591-594.
ZHANG Baozhen. Development and Applications of Integrated Diagnostics, Prognostics and Health Management Technologies of Abroad[J]. Computer Measurement & Control,2008,16(5):591-594.
[2] 张宝珍,曾天翔.先进的故障预测与状态管理技术[J].测控技术,2003,22(11):26-31.
ZHANG Baozhen, ZENG Tianxiang. Advanced Prognostics and Health Management Technology[J]. Measurement and Control Technology,2003,22(11):26-31.
[3] Adams C, Zimmerman J. Joint strike fighter: Faster, cheaper, simpler support[J]. Avionics Today, April,2003.
[4] 冯长建.HMM动态模式识别理论,方法以及在旋转机械故障诊断中的应用[D].杭州:浙江大学,2002.
FENG Changjian. HMM Dynamical Pattern Recognition Theories, Methods and Applications in Faults Diagnosis of Rotating Machine[D]. Hangzhou: Zhejiang University,2002.
[5] Vapnik V. The nature of statistical learning theory[M]. Springer Science & Business Media,2000.
[6] 张艳.基于粒子群优化支持向量机的变压器故障诊断和预测[D].成都:西华大学电气及其自动化学院,2011.
ZHANG Yan. Transformer Fault Diagnosis and Prediction Based on Particle Swarm Optimize Support Vector Machine[D]. Chengdu: Xihua University, School of electrical and automation,2011.
[7] Eberhart K. A New Optimizer Using Particle Swarm Theory[J].Proceedings of the Sixth International Symposium on Micro Machine and Human Science,Nagoya,1995:39-43.
[8] 高芳,崔刚.智能粒子群优化算法研究[D].哈尔滨:哈尔滨工业大学,2008,6:11-26.
GAO Fang, CUI Gang. Research on Intelligent Particle Swarm Optimization Algorithm[D]. Harbin: Harbin Institute of Technology,2008,6:11-26.
[9] 李宁.粒子群优化算法的理论分析与应用研究[D].武汉:华中科技大学,2007:24-67.
LI Ning. Analysis and Application of Particle Swarm Optimization[D]. Wuhan: Huazhong University of Science and Technology,2007:24-67.
[10] Kennedy J. The partical swarm:social adaptation of knowledge[J]. Proceedings of IEEE International Conference on Evolutionary Computation,1997:303-308.
[11] 张晓南,张宏梅.基于优化PSO-SVM模型的软件可靠性预测方法[J].计算机应用,2011,31(7):1762-1764.
ZHANG Xiaonan, ZHANG Hongmei. Software reliability prediction based on improved PSO-SVM model[J]. Journal of Computer Application,2011,31(7):1762-1764.
[12] 刘丽芳,张文爱.粒子群算法的改进及应用[D].太原:太原理工大学,2008,5:10-13.
LIU Aifang, ZHANG Wenai. Modification and Application of Particle Swarm Optimization Algorithm[D]. Taiyuan: Taiyuan University of Technology,2008,5:10-13.
[13] 于美娟,马希荣.基于SVM和HMM混合模型的动态手势识别技术研究[D].天津:天津师范大学,2011,6:25-37.
YU Meijuan, MA Xirong. The Research of Dynamic Gesture Recognition Technology Based on SVM and HMM Hybrid model[D]. Tianjin: Tianjin Normal University,2011,6:25-37.
中图分类号TP277
DOI:10.3969/j.issn.1672-9722.2016.01.005
作者简介:李小珉,女,副教授,硕士生导师,研究方向:电路与系统的研究。张波,男,硕士研究生,研究方向:综合测试与故障诊断。尹明,男,讲师,研究方向:电子装备测试技术。
收稿日期:2015年7月10日,修回日期:2015年8月26日

