基于CAD几何的数值流形方法初步研究

陈积瞻,苏海东,祁勇峰

（长江科学院a.水利部水工程安全与病害防治工程技术研究中心；b.材料与结构研究所,武汉 430010)



基于CAD几何的数值流形方法初步研究

陈积瞻a,b,苏海东a,b,祁勇峰a,b

（长江科学院a.水利部水工程安全与病害防治工程技术研究中心；b.材料与结构研究所,武汉 430010)

摘 要：计算机辅助工程中的设计—分析—再设计的反复过程,蕴含着计算机辅助设计（CAD)与计算机辅助工程分析（CAE)相融合的迫切需求。提出基于CAD几何的数值流形方法:按照CAE真实物理场分布的复杂程度来布置数学网格和设置近似函数阶次,比等几何分析方法更合理；只需引入自动且快速的切割操作,就能实现CAD模型进入CAE后无需修改而直接建模；针对以往的流形法需要将曲线边界离散成折线的问题,给出了曲线边界与网格直边的切割算法,实现了几何模型在CAE建模和网格细化中的保形性；针对流形法通常使用的多项式近似函数,推导了曲线“近似”单纯形的解析积分公式并应用于带有曲线边界的流形元的精确积分运算；最后通过平板内的圆孔算例验证了方法的可行性。该方法对CAD和CAE的融合提出了全新的思路,为实现CAD进入CAE后的自动化分析打下了基础。

关键词：数值流形方法；等几何分析方法；CAD几何；曲线与直线的切割；单纯形积分；CAD/ CAE协同

2016,33（02):137-143

1 研究背景

随着计算机科学与数值分析技术的迅速发展,计算机辅助工程包括计算机辅助设计（CAD)与计算机辅助工程分析（CAE)等,已成为现代设计的主要工具和手段［1］。应用CAE数学模型替代以往的物理模型对设计结果进行分析和评价,可为改进、优化设计提供重要依据。这种设计—分析—再设计的反复过程,蕴含着CAD设计与CAE分析相融合（又称为CAD和CAE协同设计与分析)的迫切需求。我们认为,最终目标是实现CAD进入CAE后的自动化分析。

计算分析方法和软件是CAE的关键因素［1］。目前,有限元方法是应用最为广泛的分析方法,但有限元网格需要适应材料边界并保持单元合适形状的硬性要求带来了2方面的影响:其一,CAD几何模型在进入CAE时一般要经过修剪、整理与简化,如去掉小的圆形倒角并进行细节修补、曲线或曲面（本文以下部分均以曲线为例)边界的分段简化（如线性化)等；其二,对形状复杂的结构进行有限元网格划分往往非常困难。因此需要大量繁琐且非常耗时的人工操作,而最令分析人员头疼的是设计—分析反复过程导致的因设计变更而重复建模。虽然一些大型商用有限元软件如ANSYS旗下的协同分析平台以及MSC公司最新推出的APEX平台等,提供了一定程度的“智能化”协同分析和网格划分功能,但离分析人员的预期仍有不小的距离,这是由于有限元方法自身的局限性使之在CAD和CAE融合方面存在一定的困难。

2005年,Hughes等［2］提出了等几何分析方法,在几何模型和分析模型中采用一套描述方式——通常是NURBS（Non-Uniform Rational B-Splines非均匀有理B样条),解决了传统数值计算的求解域描述与几何设计之间不相兼容的问题,实现了CAD和CAE的无缝连接。CAD模型可直接参与CAE分析而无需再划分网格,避免了设计与分析之间过多的人工交互以及设计修改后的分析模型重建。同时,该方法具有几何模型的精确性,即保形性:在CAE建模时避免了因几何模型简化而产生的误差,且网格细分后仍保持原有边界曲线的几何特征［3］。另外还具有近似函数的高阶连续性,计算精度相对较高。等几何分析方法提出了CAD和CAE融合的新思路,成为国际上的研究热点。

然而,等几何分析方法也存在诸多不足:工业界通常采用以边界数据表示的几何模型,与等几何分析要求的基于实体造型的几何模型不匹配［4］,而要求工业界为了适应某种计算方法而改变现状是很难的,反之,将边界模型转化为实体模型,无异于做一次完整的网格剖分；该方法采用的样条形函数具有多维基函数的张量积特征,形成的网格在拓扑上是规整的［4］,对于复杂求解域的适应性以及局部的网格细化不如有限元法方便；“等参”是等几何分析的基础,而“等参”带来的实际物理域映射到标准参数域的一些问题,比如,网格扭曲（相对于规则网格)、曲线边界（相对于直线边界)所造成的多项式精度阶次降低,数值积分精度难以把握等,也会被带入等几何分析方法［4］；笔者认为该方法最主要的问题是,“等几何”将物理场的复杂性和几何描述的复杂性等同起来,然而实际情况是,几何描述简单或复杂并不意味着物理场也同样简单或复杂,因此在计算效率方面值得讨论；同时,等几何分析中的NURBS基函数及其导数的计算远比有限元法复杂［4］。

本文基于数值流形方法,提出CAD与CAE融合的另一种新思路:根据该方法“构造近似函数的数学网格与描述求解域的几何模型相互独立”的特点,只需引入自动且快速的切割操作,就能实现CAD几何模型无需修改而直接进行CAE建模,其中,采用曲线几何边界与直线网格边界的切割,实现CAE建模和网格细化的保形性；针对多项式级数的近似函数,采用单纯形（包括具有曲线边界的“近似”单纯形)积分法进行刚度矩阵和荷载向量各项中的被积函数的解析积分；最终目标是采用自动化的前处理并根据误差估计来控制计算精度,实现CAD进入CAE后的自动化分析,即CAD和CAE的完全融合。

2 数值流形方法与CAD几何

1991年,石根华博士首次将现代数学“流形”思想引入工程计算,发明了数值流形方法［5-6］（以下简称流形法),其中很关键的一点是:与有限元法将求解域离散成网格的方式不同,流形法构造物理场近似解的所谓“数学网格”与实际求解域分离（求解域只用于定义积分区域),要求数学网格在空间上完全覆盖求解域。如图1所示,图中着色的椭圆形求解域被矩形数学网格完全覆盖。

对应于数学流形中的“覆盖”,数学网格又被称为数学覆盖。数值计算中,在各覆盖上定义覆盖函数Vi,通过单位分解函数φi联系起来形成整体近似函数（n为覆盖数)。覆盖函数Vi常用多项式级数。

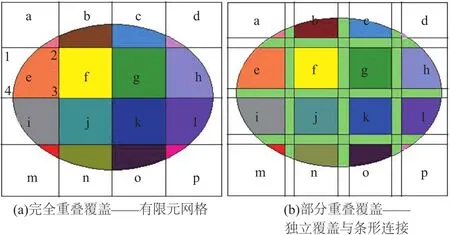
图1 矩形数学覆盖与求解域示意图Fig.1 Schematic diagrams of rectangular mathematical covers and solving domain

从数学网格（数学覆盖)的形式上看,流形法的研究分为2大类:

（1)传统流形法的数学网格大都采用有限元网格［7］,如图1（a)所示的矩形网格,这种覆盖形式称为完全重叠的数学覆盖［8］。在有限元结点上定义级数作为覆盖函数,单位分解函数就是有限单元的形函数。其网格细化仍要采用有限元网格的加密方式。

（2)非有限元的数学网格,目前主要是文献［8］提出的部分重叠覆盖的数学网格,引入了“独立覆盖”,即单位分解函数φi＝1、近似函数V就是给定级数Vi的覆盖区域。如图1（b)所示,图中的大矩形就是独立覆盖,各覆盖仅在条形区域重叠。建议条形厚度取较小值,其单位分解函数φi取为有限单元形函数（如2个覆盖之间的条形为一维线性函数)实现覆盖之间的线性过渡。该方法又被称为基于独立覆盖的数值流形方法［9］,其一大优势是覆盖加密方便,如图2所示,在大的矩形覆盖中划分小覆盖,可保证近似函数的协调性,已被证明能有效提高精度［10］。

图2 矩形独立覆盖的加密Fig.2 Refinement of rectangular independent covers

有别于等几何分析法的CAE“等几何”特性,流形法具有CAE数学网格与CAD几何模型的相互独立性,根据CAE真实物理场分布的复杂程度来布置数学网格和设置近似函数阶次,这种分析方式更为合理。但等几何分析法可以直接利用CAD实体几何模型的网格作为CAE分析模型的网格,而流形法要单独生成数学网格,通常采用如图1所示的简单且可自动生成的数学网格,需要付出数学网格与几何边界进行切割的代价。考虑到这种切割操作只涉及简单的几何运算,能够自动且快速地完成,因此流形法的前处理同样比有限元法简单得多,可做到完全的自动化。

如图1所示,经过切割操作后,在数学网格内有可能形成不能占满整个网格的物理区域（数学网格内的物理区域称为流形元),以图1中的矩形网格c为例,如图3所示,由顶点P1,P2,P3,P4,P5,P6,P7所组成的流形元具有不规则的形状,其中P1至P5是由离散的折线来近似边界曲线。对于任意形状的流形元,当近似函数为多项式级数时,通常采用单纯形积分公式［6］进行解析积分。如图3所示,将相邻顶点构成的线段依次与某一外点P0（通常取为坐标原点)相连形成一个有向单纯形,可取逆时针顶点顺序为正向,如P2,P1,P0等为正向,而P7,P6,P0和P1,P7,P0为负向。这样,对于刚度矩阵和荷载向量各项中的被积函数经整理后［11］形成的各单项式xm1ym2（m1, m2为正整数),在各单纯形中可得到精确的积分,考虑积分区域的正、负向后,累加得到整个流形元上的精确积分。

图3 单纯形积分示意图Fig.3 Schematic diagram of simplex integration

当CAD几何模型进入CAE后,无需像有限元法那样进行“去倒角”等细节修补工作,因为倒角是几何边界的一部分,它与CAE数学网格没有关系,可以保留作为网格内的流形元边界的一部分。

图4 CAD曲线边界的线段化Fig.4 Process of changing CAD curve boundaries to line segments

与等几何分析方法相比,现有的流形法仍然需要将曲线边界线性化（线段化),如图4所示。这会带来几个不利影响:首先,在CAE分析中会造成几何模型误差,且网格细分时面对的是已经线性化的几何边界；其次,在CAE分析前就要预估线性化的程度（如将曲线划分为多少直线段),这需要分析人员具有一定的经验；同时,对于每条线段都要进行一次单纯形积分,若为减小几何误差而划分较多线段,可能会影响计算效率,特别是对于小的圆形倒角情况。以上问题造成了流形法在CAD和CAE系统之间的不匹配。

因此,本文除了以上的论述——分析流形法在CAD和CAE融合中的特色外,下面的主要工作就是要做到保形性,即在分析模型构造和网格细化以及计算分析过程中保持原有的几何形状。本文以平面计算为例,仅需两项工作:曲线几何边界与直线网格边界的切割；曲线边界“近似”单纯形的解析积分。

3 曲线几何边界与直线网格边界的切割

数学网格和几何模型边界的切割操作,只涉及简单几何运算。目前的流形法基于直线段的切割,已有成熟算法和程序,主要过程如下［6］:①将数学网格和几何边界线段化,每个数学网格的边和每条描述边界的折线都各自作为一条线段；②所有线段之间相互切割；③根据每条线段上记录的交点位置顺序及每个交点对应的线段序号,按照一定规则确定环路,同时删除不能形成环路的“树枝”,在求解域内的每个环路就是一个流形元；④根据流形元的形心判断它属于哪个数学网格。

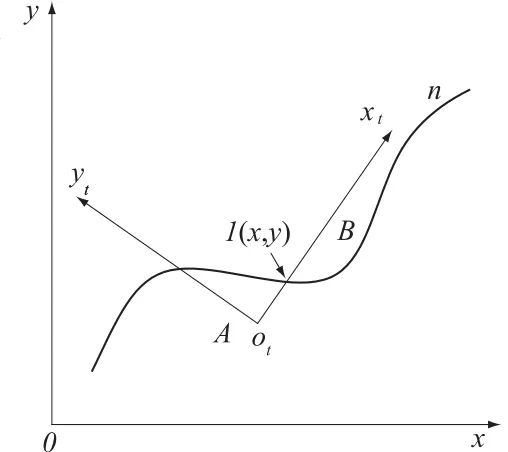
图5 坐标转换Fig.5 Coordinate transformation

本文中,过程①的曲线几何边界无需变成折线,直接进入过程②与直线网格边界进行切割。切割算法如下:如图5所示,设曲线n可表示为

求其函数与直线段A （xa,ya)—B（xb,yb)的交点。

将整体坐标系转换到以A（xa,ya)为原点、AB方向为xt轴的局部坐标系（xt,yt)

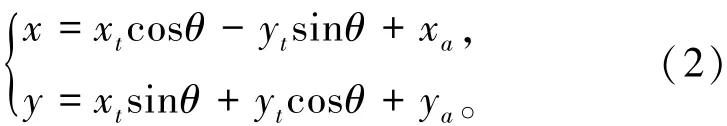
式中θ为AB线段与整体坐标x轴的夹角。则式（1)为

设局部坐标下的交点为（xt,0) ,令xm＝xtcosθ＋xa,则式（3)为

利用二分法求得xm的值,即可求出xt,再利用式（2)得到整体坐标系下的交点坐标（x,y)。在多个交点情况下可参考文献［12］进行求解。

对于圆、椭圆曲线,虽然整体上不能简单表示成式（1)的函数形式,但可以用分段函数表示。或者采用其他方式,如图6所示的以O为圆点的圆弧与直线MN相交,记交点为J（x,y) ,则OM大于半径,ON小于半径,按二分法迭代求解,当OJ等于半径时即为交点。

可见,曲线与直线求交方式多样化,是由曲线种类的多样性决定的。在CAD中,可将一些复杂曲线统一由NURBS表示,而NURBS与直线求交的算法已很成熟,限于篇幅不再详述。

图6 圆弧与直线段相交Fig.6 A circle arc intersected by a line segment

当然,曲线与直线求交的运算量要远大于直线之间求交的运算量,因此为提高效率,事先要排除无关的直线段,如图7（a)所示的曲线n ,采用包围盒子法［13］排除盒子（图中虚线)外的无关线段,再区分图7（b)的几种直线情况:首先按函数值排除法,如直线段5和6的首尾端点的函数值均在曲线上方或下方；然后,直线段2和3的某一端点在曲线上,则交点为其端点；竖直的线段4,将x坐标代入曲线方程即可求得y坐标；最后才用图5所示的坐标转换及二分法处理直线段1。

图7 包围盒子法及交点的多种情况Fig.7 Bounding box method and some circumstances of intersection points

4 曲线边界“近似”单纯形的解析积分

仍以图1中的矩形网格c为例,与图3中将流形元曲线边界转化为多条折线的方式不同,如图8（a)所示,P1到P5仍用原始曲线表示,将其与P0相连,构成一条边为曲线的“近似”单纯形,如图8 （b)所示,其解析积分分为2部分:一部分是直线边的单纯形,按常规单纯形公式［14］计算；另一部分是P1PkP5,其积分下限为P1到P5的直线,积分上限为P1到P5的曲线。以下讨论后一部分。

图8 含一条曲线边的“近似”单纯形Fig.8 An approximate simplex containing a curved edge

设作为积分上限的曲线表述为多项式函数

m为多项式的最高阶次,不能写成函数形式时可分段表示为函数。作为积分下限的直线为

其中, ai, bi为已知系数。曲线两端点为（x1,y1)、（x2,y2) ,被积函数f（x,y)为xm1ym2,则

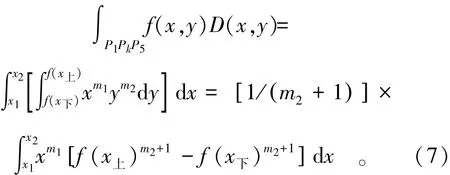
记:L＝1/（m2＋1)；Am＝[a0a1…am]T；Xm＝[x0x1…xm]T；B＝[b0b1]T；m＝m＋1,化简

102为

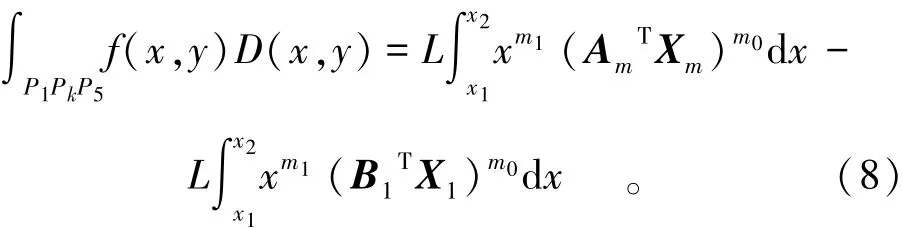
关键是求出下式的精确解,

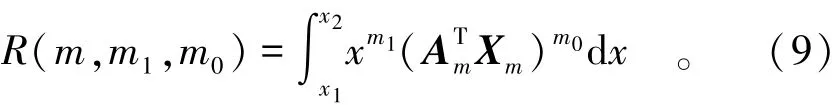
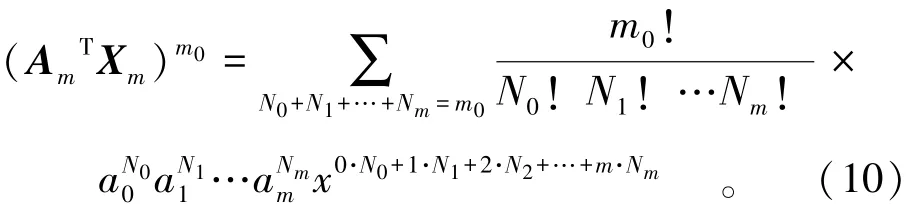
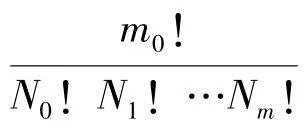
展开式中仍有同类项需要合并,若各项的幂次0·N0＋1·N1＋2·N2…＋m·Nm相等,则标记为同类项,合并后一共有m·m0＋1项,记各项系数为Kj（j是从0至m·m0＋1递增的整数),则式（9)可写为

可见,随j增大的各项按照x的幂差为1的次序递增,为编程提供了良好的递推规律,即后项比前项多乘一个x1和x2。

上述方法理论上对于积分上限为任意多项式的曲线均可以计算,但如果描述曲线的多项式阶数过高,则计算量较大,且容易引入数值误差。考虑到一般计算中的数学网格不至于很大,网格内的曲线也不会过于复杂,2阶或3阶多项式就可以很好地描述,因此,建议首先用2阶或3阶多项式逼近网格内的复杂曲线（可以是任意表达式,如NURBS,还包括高于3阶的多项式),再利用上述公式进行解析积分。

对于曲线边界l上的分布力荷载,设分布力p＝[Px,Py]T,其荷载向量中的被积函数也分解成单项式xm1ym2的形式［11］。考虑l为二次曲线y＝∑i＝20aixi,导数为y′＝a1＋2a2x。若计算的正压力荷载为线性分布P＝c0＋c1x＋c2y ,则Px＝Pcosθ,Py＝Psinθ（θ为曲线上某点的法线与坐标x轴的夹角),

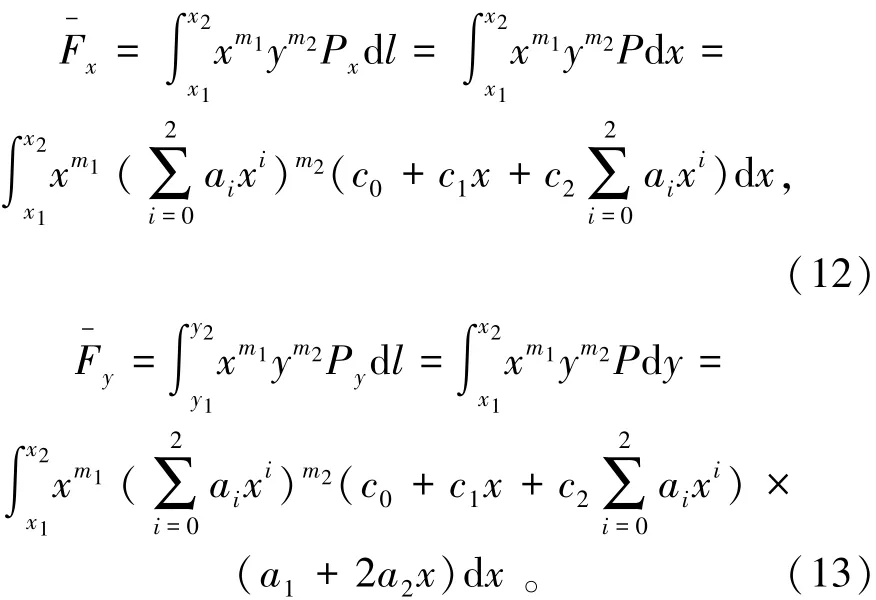
其最终仍可归结为求式（9)中R的解析积分。

5 算 例

中部开小圆孔（半径为1 m)的矩形板在上、下两端受均布拉力p＝10 kN/ m2,基于对称性,采用如图9（a)所示的1/4计算模型,左边和底部用积分形式的罚函数法施加法向约束。计算圆孔中部边界点的应力集中系数,理论值是3。

采用如图1（b)所示的基于矩形独立覆盖的新型流形法,充分利用其覆盖网格自动生成、h型覆盖加密以及p型升阶方便的优势,在误差指标控制下尝试h-p型混合自适应,初步实现了CAE自动化分析:结构外形（含曲线边界)由CAD输入,人工只需输入材料参数和边界条件,其它所有工作完全交由计算机完成（另文介绍)。

最终的流形元网格如图9（a)所示,圆孔周边局部在图9（b)中放大,1/4圆弧被矩形网格分为5段,分别位于3个独立覆盖及2个条形内。在包含上述曲线边界的流形元的积分运算中,取每段圆弧中点及2个端点的坐标为插值点,采用2阶多项式逼近圆弧边界。计算程序自动设置独立覆盖的多项式阶次:大多数为2阶,只在圆孔周边的少数几个覆盖用到3至4阶多项式。自由度总数为462。

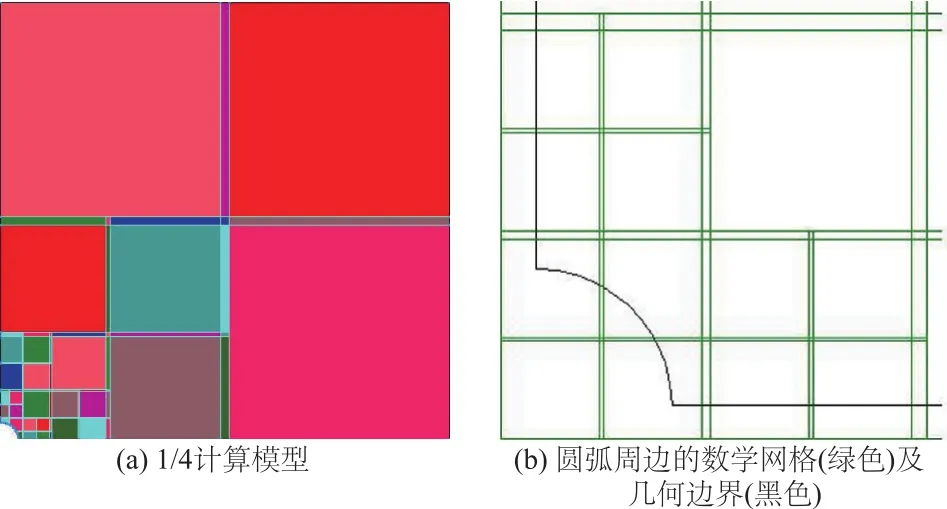
图9 圆孔算例的1/4计算模型Fig.9 1/4 model of a rectangular plate with a small circular hole

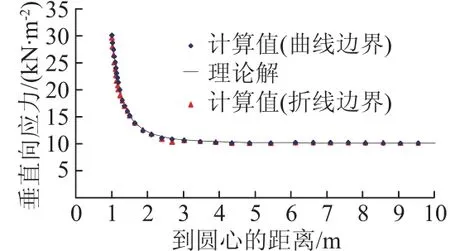
图10 垂直向应力与理论值的对比Fig.10 Comparison between calculated data and analytical data of vertical stress

计算得到的底部一条线上的垂直向应力σy见图10（标注“曲线边界”),可见与理论解［16］很好地符合。其中圆孔边界点的σy为30.16 kN/ m2,应力集中系数约为3.02,与理论值非常接近,自由表面应力σx和τxy分别为0.09 kN/ m2和0.05 kN/ m2,与理论上的零应力也非常接近。

另外按传统方法,1/4圆弧用10段折线离散,其他条件不变。计算得到圆孔边界点的σy为29.66 kN/ m2,应力集中系数约为2.97。底部一条线上的垂直向应力σy如图10所示（标注“折线边界”),虽然也与理论解较吻合,但不如曲线边界的计算精度高,不难看出几何误差带来的影响。

6 结 语

本文提出基于CAD几何的数值流形方法,与等几何分析方法相比具有以下特点:采用工业界通用的以边界数据表示的CAD几何模型；在CAE建模和网格细化中同样具有几何模型的保形性,避免了几何误差；针对流形法通常使用的多项式近似函数（其计算过程比等几何分析中的NURBS基函数要简单),采用单纯形精确积分法实现任意形状流形元的解析积分,没有等几何分析方法的“等参”方式所带来的诸多问题。

在等几何分析方法中,CAD实体模型与CAE分析模型相同。考虑到几何描述的复杂性并不等同于物理场的复杂性,本文方法根据真实物理场分布的复杂程度来布置数学网格和设置近似函数阶次,似更为合理。而且只需采用自动且快速的切割操作,也能实现CAD模型无需修改而直接在CAE中建模,甚至完全自动化的前处理。配合使用基于独立覆盖的新型流形法,网格加密很方便,对复杂求解域的适应性更强。只是本文方法的近似函数不具备等几何分析方法的高阶连续性。

因此,本文方法为CAD与CAE融合提供了全新的思路,最终能够实现CAD进入CAE后的自动化分析（另文介绍),即CAD和CAE的完全融合。当然,本文仅对二维问题开展了初步研究,提出的切割算法、“近似”单纯形积分算法只为说明方法的基本学术思想,算法的适用性及效率等问题还有待进一步研究。在算例中虽然采用了基于独立覆盖的新型流形法,但本文方法也适用于采用有限元数学网格的传统流形法。将来扩展到三维研究,涉及曲面几何边界与平面网格边界的切割和曲面“近似”单纯形的解析积分,本文的思路同样适用。

致谢：部分重叠覆盖的思想来自于石根华博士，笔者的研究一直受到石根华博士的指导，文中有关常规单纯形积分的部分内容采用了长江科学院林绍忠教授的研究成果，在此表示由衷的感谢。

参考文献：

［1］ 百度百科.CAE［EB/ OL］.（2015-06-11)［2015-07-10］. http:/ / baike.baidu.com/ view/112169.htm.

［2］ HUGHES T J R,COTTRELL J A,BAZILEVS Y. Isogeometric Analysis: CAD, Finite Elements, NURBS, Exact Geometry and Mesh Refinement［J］. Computer Methods in Applied Mechanics and Engineering,2005,194:39-41.

［3］ 吴紫俊,黄正东,左兵权,等.等几何分析研究概述［J］.机械工程学报,2015,51（5):114-129.

［4］ 夏 阳.假设位移协调有限元及其在精确几何分析中的应用［D］.大连:大连理工大学,2013.

［5］ SHI G H. Manifold Method of Material Analysis［C］/ / U. S. Army Research Office. Transactions of the Ninth Army Conference on Applied Mathematics and Computing, Minneapolis, Minnesota, U S A, June 18-21,1991:57-76.

［6］ 石根华.数值流形方法与非连续变形分析［M］.裴觉民译.北京:清华大学出版社,1997.

［7］ 张湘伟,章争荣,吕文阁,等.数值流形方法研究及应用进展［J］.力学进展, 2010, 40（1): 1-12 .

［8］ 祁勇峰,苏海东,崔建华.部分重叠覆盖的数值流形方法初步研究［J］.长江科学院院报, 2013,30（1):65-70 .

［9］ 苏海东,颉志强,龚亚琦,等.基于独立覆盖的流形法的收敛性及覆盖网格特性［J］.长江科学院院报, 2016,33（2):131-136.

［10］苏海东,祁勇峰.部分重叠覆盖流形法的覆盖加密方法［J］.长江科学院院报, 2013, 30（7):95-100.

［11］林绍忠,祁勇峰,苏海东.基于矩阵特殊运算的高阶流形单元分析［J］.长江科学院院报, 2006,23（3):36-39.

［12］林 永,陈 浩.用二分法求解一元实系数多项式方程的全部实根［J］.大学数学,2008,24（4):89-91 .

［13］孙家广,杨长贵.计算机图形学［M］.北京:清华大学出版社,1995.

［14］林绍忠.单纯形积分的递推公式［J］.长江科学院院报, 2005,22（3):32-34.

［15］苏方方.动态规划算法计算组合数Cmn［J］.现代计算机,2011,（10):35-37.

［16］徐芝纶.弹性力学（第2版)［M］.北京:人民教育出版社,1982.

（编辑:刘运飞)

Preliminary Study of Numerical Manifold Method Based on CAD Geometry

CHEN Ji-zhan1,2,SU Hai-dong1,2,QI Yong-feng1,2
（1. Research Center on Water Engineering Safety and Disease Control Engineering Technology under Ministry of Water Resources, Yangtze River Scientific Research Institute, Wuhan 430010, China；2. Material and Engineering Structure Department, Yangtze River Scientific Research Institute, Wuhan 430010, China)

Abstract:The iterative process of design-analysis-redesign implies urgent requests of the integration of computer aided design（CAD) and computer aided engineering（CAE). In this paper, we present a numerical manifold method（NMM) based on CAD geometry: we can arrange mathematical meshes and set order of approximation functions according to the complexity degree of physical field distribution in CAE, which is more reasonable than isogeometric analysis（IGA) method. Through introducing automatic and fast cutting operations, we can realize direct modeling from CAD model to CAE model without modifications. Moreover, to solve the problem that curves on geometric boundaries are required to be discretized into line segments in present NMM, we put forward algorithms to cut the curves of geometric boundary with the lines of mesh boundary, hence preserving the shape of the geometric model in the procedures of CAE modeling and mesh refinement. Furthermore, as for the polynomial approximation functions usually used in NMM, we deduce analytical integral formula of“approximate”simplex with a curved edge and use it to obtain precise integral calculations of manifold elements with curved boundaries. Finally, we verify the feasibility of the method through an example of a circular hole in a plate. The research offers new thinking for the integration of CAD and CAE, and lays foundation for the automatic analysis from CAD models to CAE.

Key words:numerical manifold method（NMM)；isogeometric analysis（IGA)；CAD geometry；cutting of curves and lines；simplex integration；CAD/ CAE cooperativity

通讯作者：苏海东（1968-),男,湖北武汉人,教授级高级工程师,博士,从事水工结构数值分析工作和计算方法研究,（电话)027-82927167（电子信箱)suhd@ mail.crsri.cn。

作者简介：陈积瞻（1990-),男,海南乐东人,硕士研究生,从事水工结构数值分析工作和计算方法研究,（电话)18827620840（电子信箱)xincunyihaoqiao@163.com。

基金项目：国家自然科学基金项目（51409012)；中央级公益性科研院所基本科研业务费项目（CKSF2014054/ CL)

收稿日期：2015-07-16;修回日期：2015-09-11

doi:10.11988/ ckyyb.20150599

中图分类号：TB115;TV311

文献标志码：A

文章编号：1001-5485(2016)02-0137-07