最小二乘法在直升机扇形应召搜潜阵中的应用*

谭乐祖　张　诗　钟文武　单　珊

(海军航空工程学院　烟台　264001)



最小二乘法在直升机扇形应召搜潜阵中的应用*

谭乐祖张诗钟文武单珊

(海军航空工程学院烟台264001)

摘要单机扇形阵是直升机应召反潜中常用的搜潜样式。扇形阵的间隔系数的大小对于扇形阵搜潜战术运用具有显著影响。依据研究问题的逻辑关系,分别建立了基于位置、航向、航速误差的潜艇仿真模型和扇形阵搜潜效能模型,通过改变间隔系数来对直升机应召搜潜扇形阵搜潜效能进行分析评估。采用最小二乘拟合的方法对结果进行拟合,求得存在潜艇速度误差和位置误差条件下的扇形阵的最佳间隔系数。

关键词航空反潜; 潜艇误差; 扇形阵; 效能模型

Application of Least Square Method in Fan-shaped On-called Anti-submarine

TAN LezuZHANG ShiZHONG WenwuSHAN Shan

(Naval Aeronautical and Astronautical University, Yantai264001)

AbstractAnti-submarine had been an important pattern of operation. Sector fanshaped tactical formation had been influenced by spacing coefficients in tactical formation. This article introduced logarithm spiral methods and built model on-call searching model for error of location and speed of submarine. Search effects on on-call logarithm spiral dipping sonar searching were assessed by changing spacing coefficients. The optimum spacing coefficients had been gotten by the least square method with the error of location and speed of submarine existing.

Key Wordsanti-submarine, submarine speed error, sector fanshaped tactical formation, effecitivenes model

Class NumberTP2

1引言

反潜作战是海军兵力主要作战任务之一。航空反潜已经成为海军兵力反潜作战的主要手段,而直升机反潜是航空反潜的重要组成部分。应召反潜是一种重要的反潜任务类型,扇形阵反潜是应召反潜中主要的搜潜样式。间隔系数的取值对扇形阵反潜效能和反潜直升机战术运用具有显著的影响。

2吊放声呐应召搜潜问题描述

2.1应召搜索简述

应召搜索是指反潜机在机场或特定空域待命,当获悉敌潜艇的活动信息后,按照上级命令飞往指定海域,对敌潜艇进行跟踪、搜索和攻击的战斗行动[1]。吊放声呐是反潜机装备的主要搜潜设备之一,具有搜索速度快、精度高、有多种工作方式、使用经济、受水文条件影响小等特点。本文通过对吊放声呐在一定条件下的搜潜效能仿真,分析了影响吊放声呐应召搜潜效能的主要因素,对提高反潜效能和吊放声呐的运用具有重要意义。

2.2吊放声呐搜潜过程分析

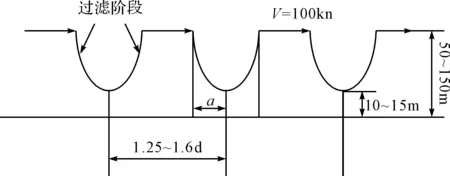
图1　吊放声呐搜索飞行剖面图

3吊放声呐应召搜潜效能仿真模型

3.1蒙特卡洛搜索模型

吊放声纳搜潜具有不确定性,本文采取统计学中的蒙特卡洛法对搜潜结果进行仿真。根据蒙特卡洛的基本思想,将吊放声纳对潜搜索这个事件作为随机试验,得到仿真结果的统计概率,作为吊放声纳搜潜效能的近似值[2]。

3.2潜艇仿真模型

1) 潜艇的初始位置服从(0,1)正态分布。设经过提供情报得潜艇的初始位置为x1、y1。通过仿真模拟产生两个随机数ξ1、ξ2。则潜艇的实际初始位置为

x=x1+ξ1

y=y1+ξ2

(1)

2) 潜艇的航速服从(v,σ)正态分布。通过仿真产生一个随机数v′,则潜艇的实际速度为v′。

3) 潜艇航向服从(0,λ)均匀分布。通过仿真产生一个随机数θ,则潜艇的任意t时刻的位置为

xt=x+v·t·cosθ

yt=y+v·t·sinθ

(2)

4) 吊放声呐探测范围是以水下分机为圆心,用战术作用距离作为半径的圆。设吊放声纳探测半径为D,则吊放声呐战术作用距离为

d=k·D(k=1.25～1.6)

(3)

3.3扇形搜索模型

扇形扩展阵适用于应召搜潜中,在目标丢失,但知道潜艇大概航向和丢失点的情况下所采用的阵法[3]。本文以k倍吊放声呐探测距离为两探测点的间距,采取扇形扩展阵的方式进行反潜搜索,具体过程如图2所示。

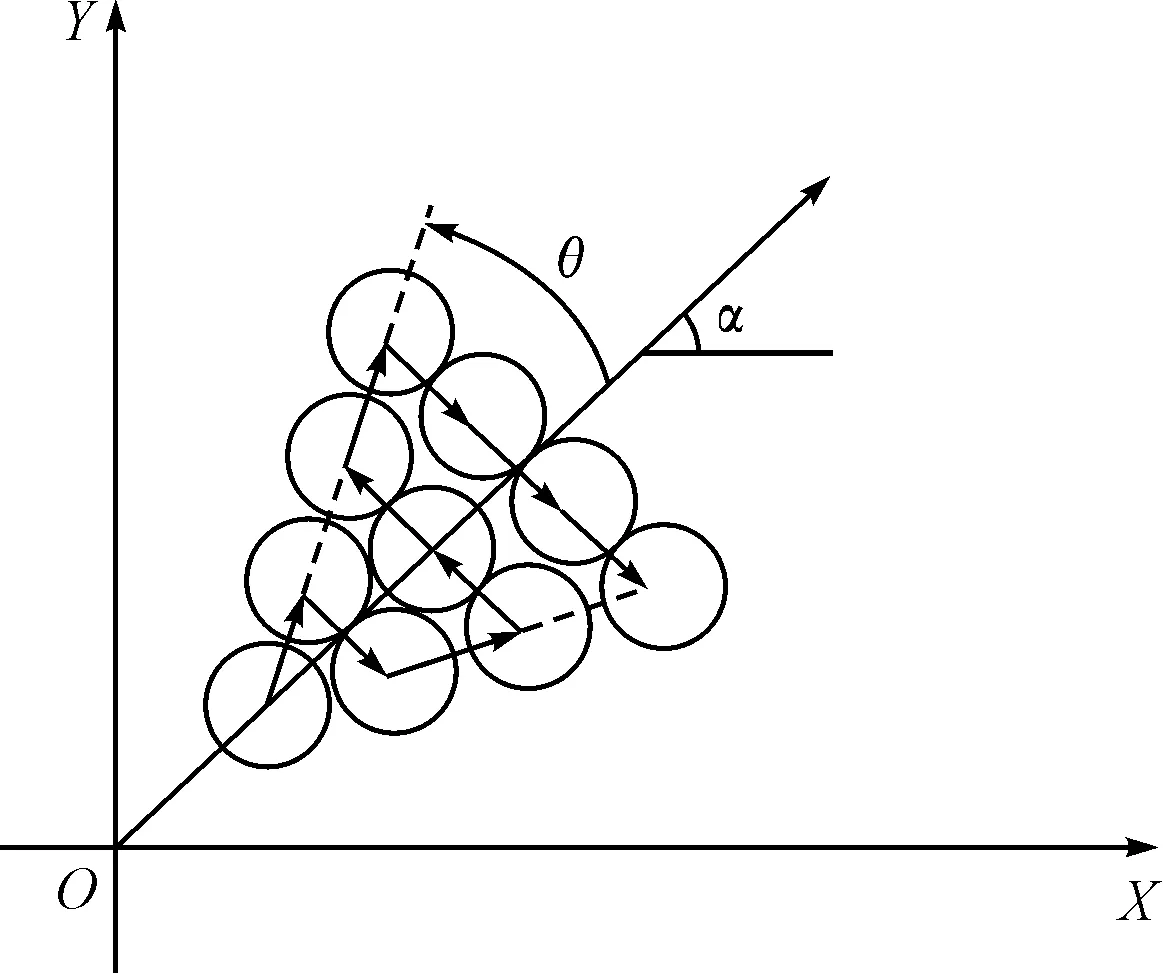
图2　扇形扩展阵示意图

根据图3可知,θ=λ/2,α为初始航向与X轴的夹角。

设Ri为初始探测点到第i行第一个探测点的距离。Li为第i行第一个探测点与最后一个探测点间的距离,Ddet为k倍战术作用距离,k为间隔系数。由图3可知:

Ri=(i-1)·Nhel·k·Ddet/cosθ

Li=2·tanθ·(i-1)·k·Ddet

(4)

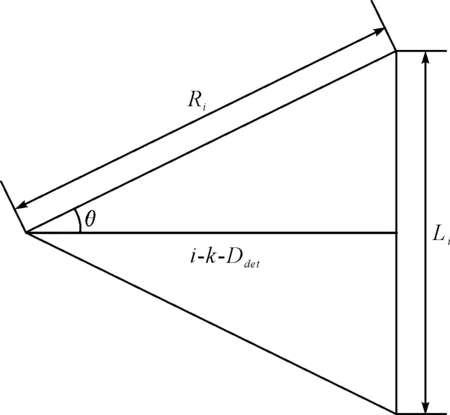
图3　扇形扩展阵搜潜数学关系模型

则第i行上探测点数目Ni取Li/(k·Ddet)的最小整数,第行相邻探测点的间距Di为

Di=Li/Ni

(5)

由此可知,第i行第j个点的坐标为

(6)

3.4最小二乘法求解间隔系数

根据扇形扩展阵的适用条件,由于潜艇的航速是未知的,随着k取值不同,搜潜结果也会产生很大的区别。如何选取k值,使得在潜艇航速未知的情况下,搜潜概率最大,对于实际作战具有重要的影响。

由于航速是完全未知的,其在(0,vmax)区间内服从均匀分布。对于固定的间隔系数ki,以u航速为一个间隔,在0～vmax范围内,分别取n个值,通过仿真求其搜潜概率,求出n个航速对应概率的总和π。求出不同的ki值,对应的概率总和π。利用最小二乘法,对数据进行多项式拟合,求出拟合曲线。通过对拟合曲线分析找到k值,使得搜潜概率最大。

4仿真分析

根据文献[4]可知,取20kn/h为目标航速的最大值,则潜艇的航速区间为(0,20),以1kn/h为航速间隔。对于固定间隔系数k,则在航速区间内,可以取20个值。

文献[5]介绍了方形扩展阵中间隔的取值范围为(1,3),以0.1为一个步长,在取值区间内,可以取得21个k值。通过仿真计算可以得到21个k值对应的搜潜概率如表1所示。

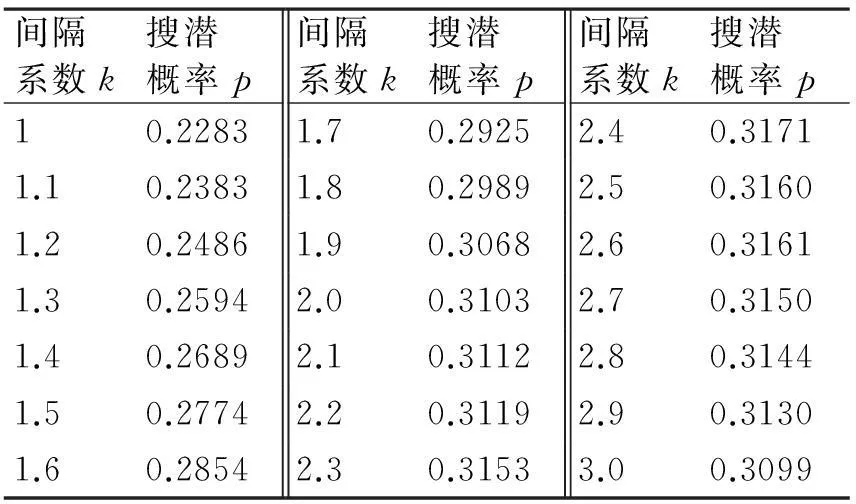
表1　间隔系数与搜潜概率关系表

以k值为x轴,以搜潜概率p为y轴,则分别取(0,20)中的整数作为潜艇的预估航速,分别在(1,3)以0.1为一个步长对k取值。对于同一个k值可以求出在n个预估航速下,每个预估航速对应的搜潜概率pi,对每个概率pi进行相加,会得到相同k值下,搜潜概率p。同理,可以求出21个k值对应的搜潜概率,如表1所示。以k为x轴,p为y轴,可以画出21个点。根据图4中点的散布可知,随着k值的增加,p值并不会一直增加或一直减小。因此不能用一次函数对其拟合。考虑到随着次数的增加,拟合的曲线具有不稳定性,本文采用二次函数对其进行拟合。

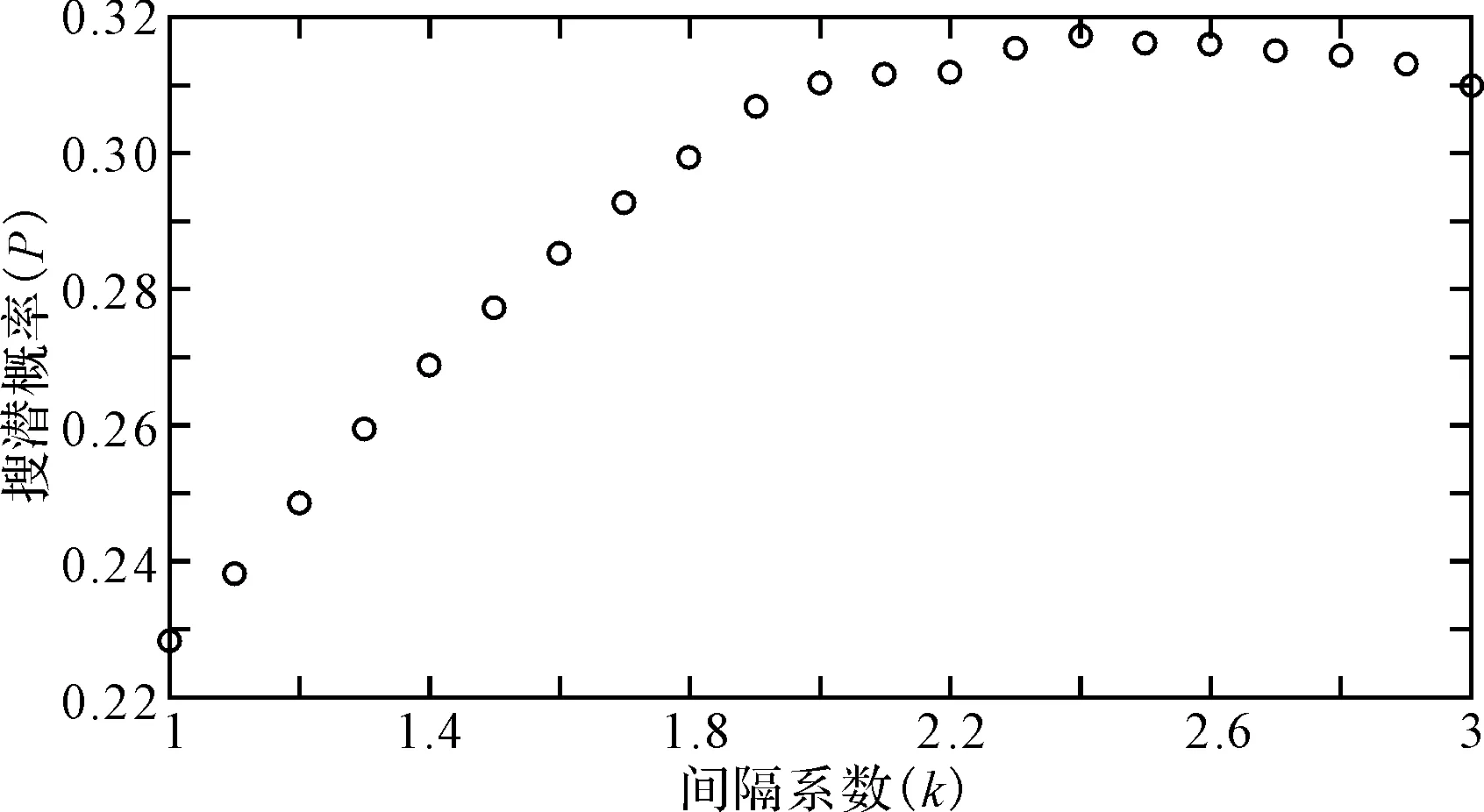
图4　间隔系数与搜潜概率散布图

设拟合函数y=aki2+bki+c,根据表1数据,可以求得表2中的各项数值。

由表2可得到对应的法方程为

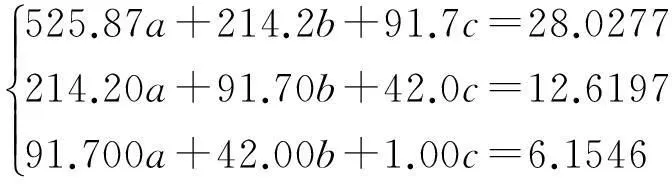
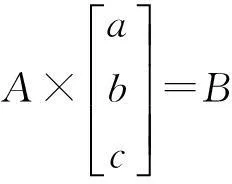
可知方程的系数矩阵:

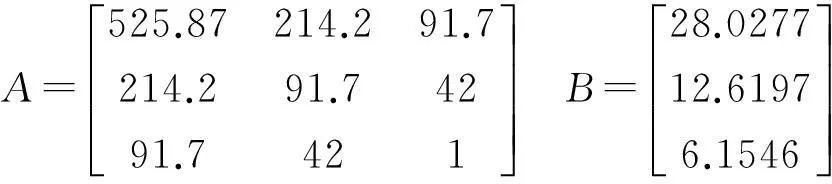
可以求得方程的解a=-1.139,b=5.418,c=-0.0105,则拟合函数为y=-1.139k2+5.418k-0.0105。对拟合函数求导数,可以求得k=2.38,搜潜概率最大,进而可以求得搜潜概率p=0.317。

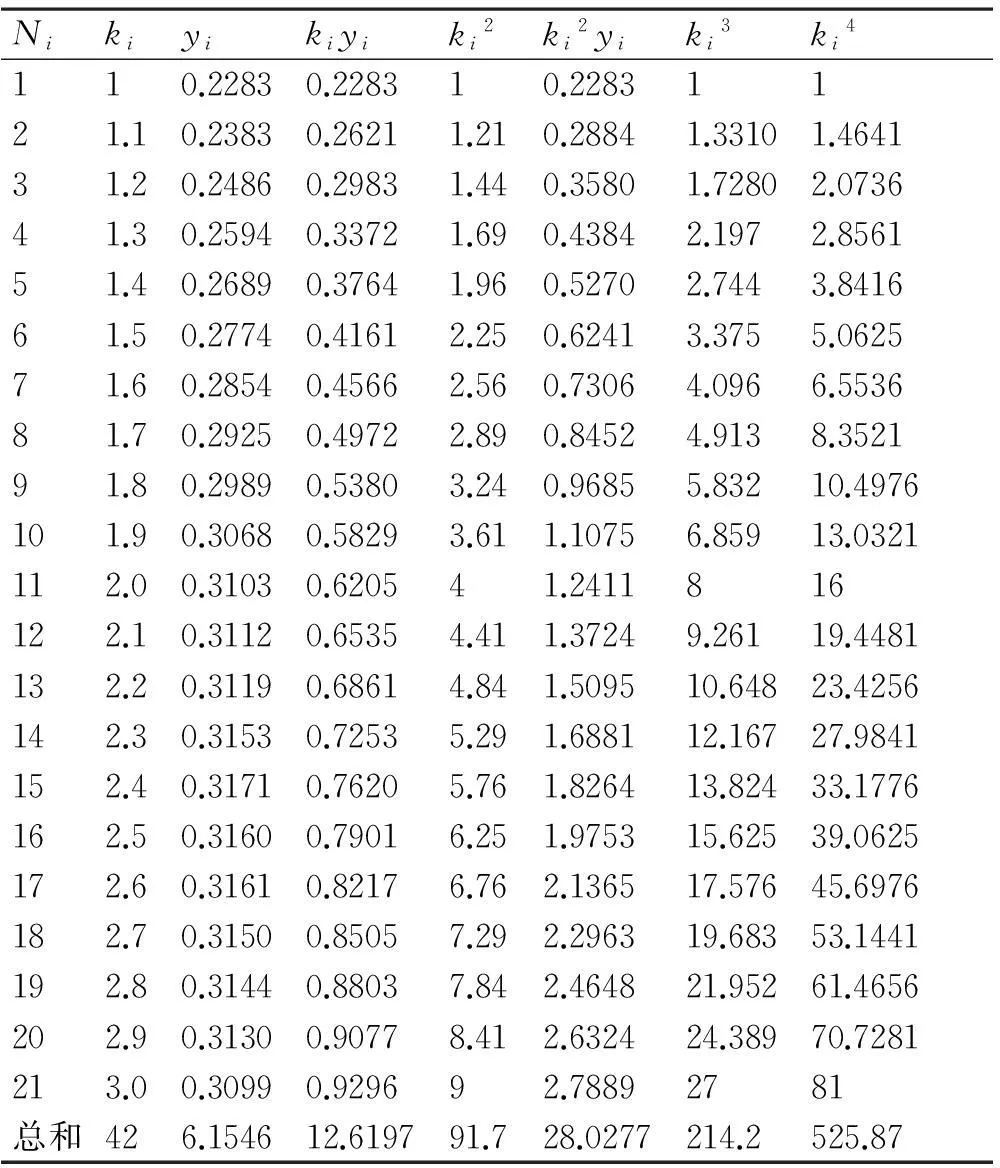
表2　间隔系数与拟合函数的关系

5结语

本文对应召搜索中,潜艇航速未知,航向在一个范围的情况进行分析,在考虑潜艇初始位置误差和航向误差的前提下,采用扇形阵对潜艇进行搜索,并利用蒙特卡洛法对搜潜结果进行仿真。通过改变间隔系数k,求得不同间隔系数对应的搜潜概率。利用最小二乘拟合的方法对搜潜概率进行拟合,得到拟合函数,通过对拟合函数求导,得到扇形阵搜索的最佳间隔系数,对实际应召搜潜作战具有重要的意义。

参 考 文 献

[1] 孙明太.航空反潜概论[M].北京:国防工业出版社,1998:344-345,351.

[2] 屈也频.反潜飞机搜潜效能评估与决策建模[M].北京:国防工业出版社,2011:35-38..

[3] 俞科云,吕云飞.潜艇时统应用与管理分析[J].舰船电子工程,2010,30(7):18-20

[4] 孙明太,等.航空反潜战术[M].北京:军事科学出版社,2003:6-10.

[5] 海航司令部.直升机反潜[M].北京:海潮出版社,1991:153,192.

[6] 吴芳,杨日杰.对潜的吊放声纳应召搜索技术研究[J].系统仿真学报,2009,21(13):3989-39.

中图分类号TP2

DOI:10.3969/j.issn.1672-9730.2016.01.006

作者简介:谭乐祖,男,教授,研究方向:作战运筹分析。

*收稿日期:2015年7月8日,修回日期:2015年8月27日基金项目:航空反潜火控技术研究(编号:20095184005)资助。