“拐点法”测普朗克常量误差大的应对方法

黄安梁，徐平川，陈金晶

(西华师范大学，四川 南充　637009)



*通讯联系人

“拐点法”测普朗克常量误差大的应对方法

黄安梁，徐平川*，陈金晶

(西华师范大学，四川 南充637009)

摘 要：由光电效应试验中得到的伏安特性曲线，用粗略简易的“拐点法”可以很快计算出普朗克常量，但计算出的数值误差比较大，针对误差较大，通过多次的取值分析计算，最后得出可以尽可能减小误差的“拐点”的确定。

关键词：光电效应；普朗克常量；拐点法；误差

1实验仪器及原理

1.1实验仪器

所用实验仪器如下：LB-PH4A光电综合实验仪器，其中包括微电流放大器，光电管工作电源，光电管盒，光电池盒，光敏电阻盒，汞灯，滤色片5组，该仪器测量误差<=3%。以及数据分析处理软件Originpro[1-2]。

1.2实验原理

光电效应的实验原理如图1所示。入射光照射到光电管阴极K上，产生光电子在电场作用下向阳极A迁移构成光电流，改变外加电压UAK，测量出光电流I的大小，即可得出光电管的伏安特性曲线[3-4]。

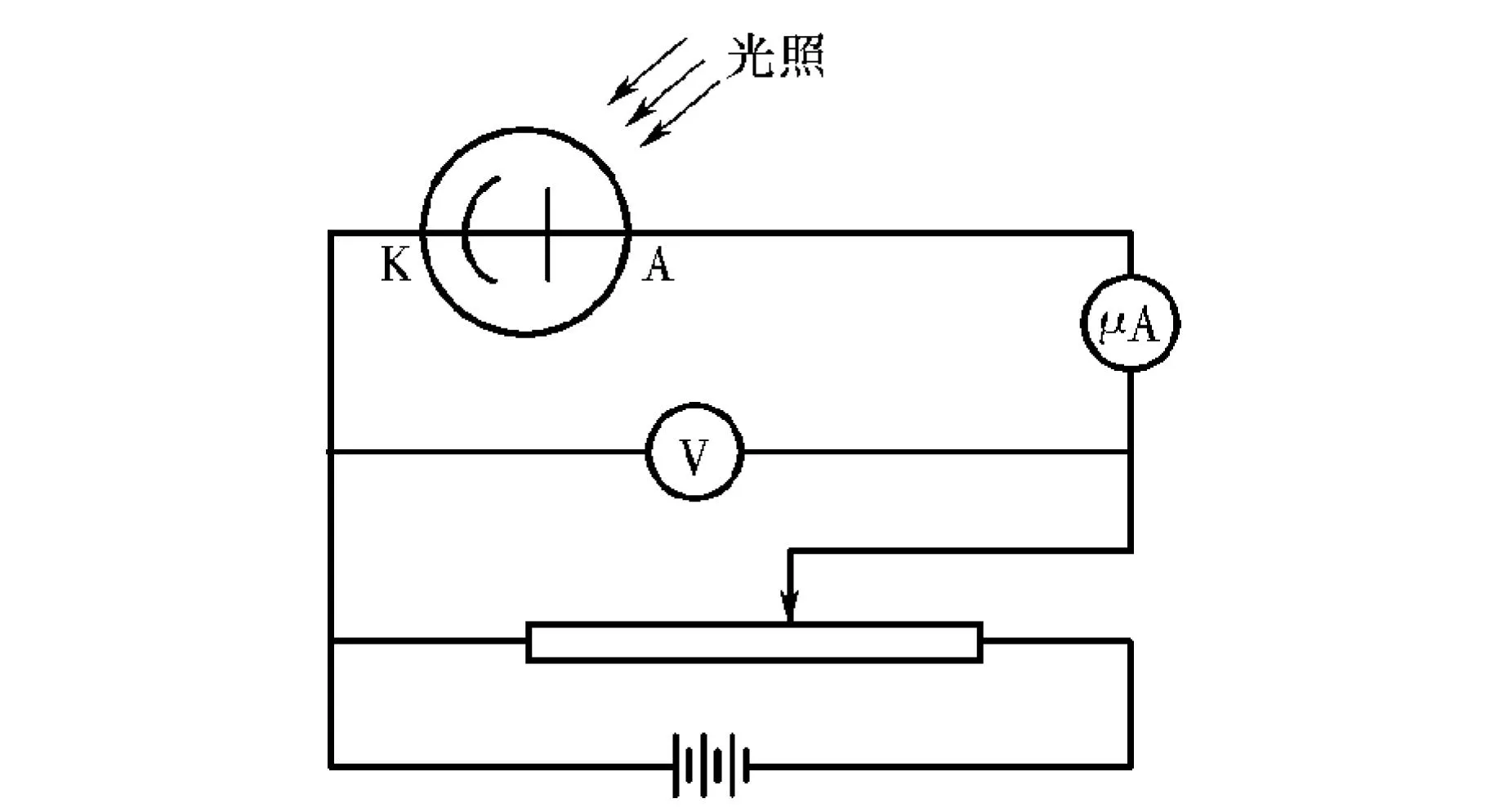
图1　实验原理图

爱因斯坦提出的光电效应方程：

hν=1/2mv2+A

(1)

其中，A是金属的逸出功，1/2mv2位光电子获得的初始动能。

由此可见，入射到金属表面的光频率越高，逸出的电子动能也就越大，所以即使阳极电位比阴极电位低时也会有电子落入阳极形成光电流，直至阳极电位低于截止电压，光电流才为零，此时有关系：

eU0=1/2mv2

(2)

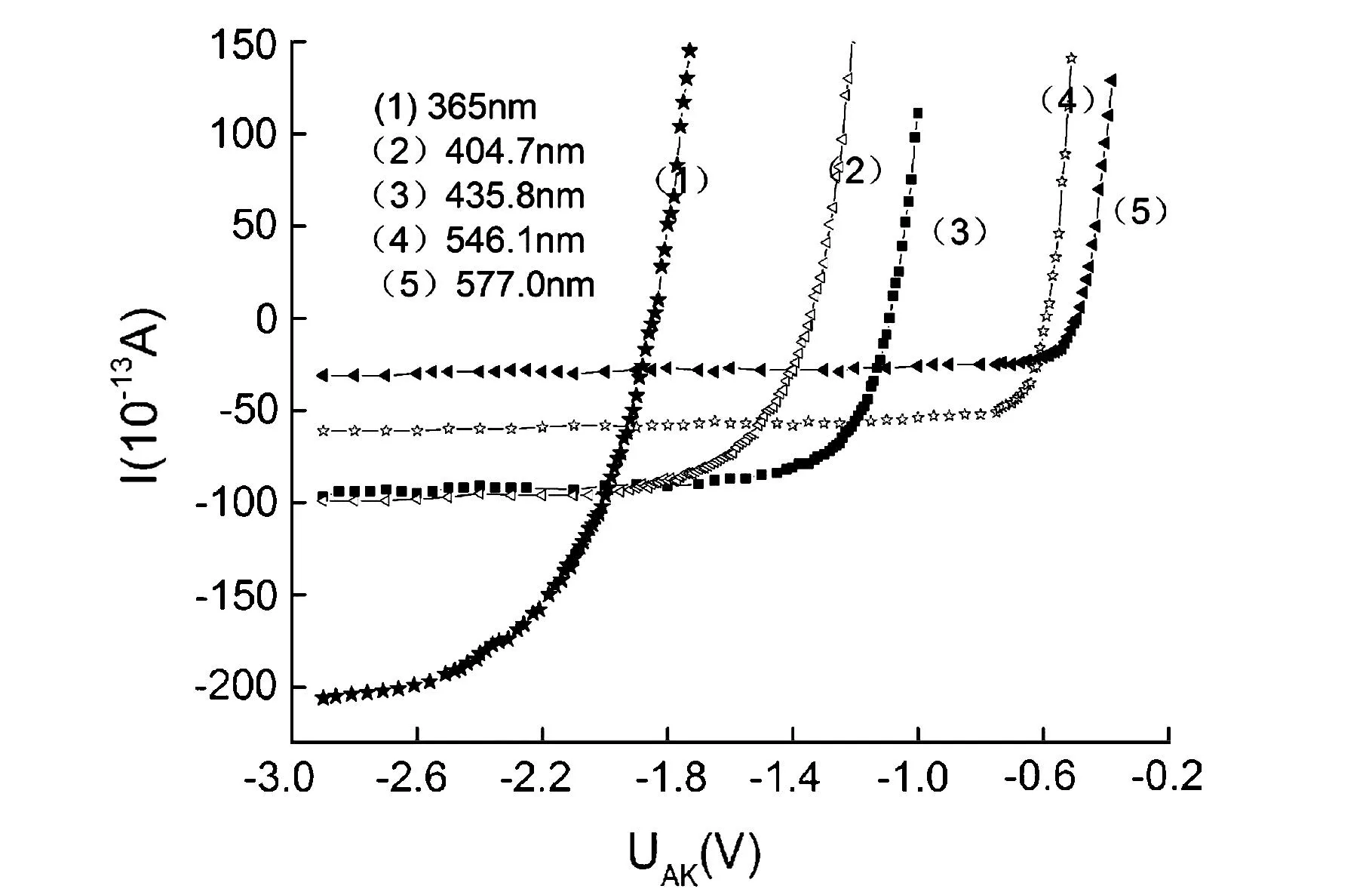
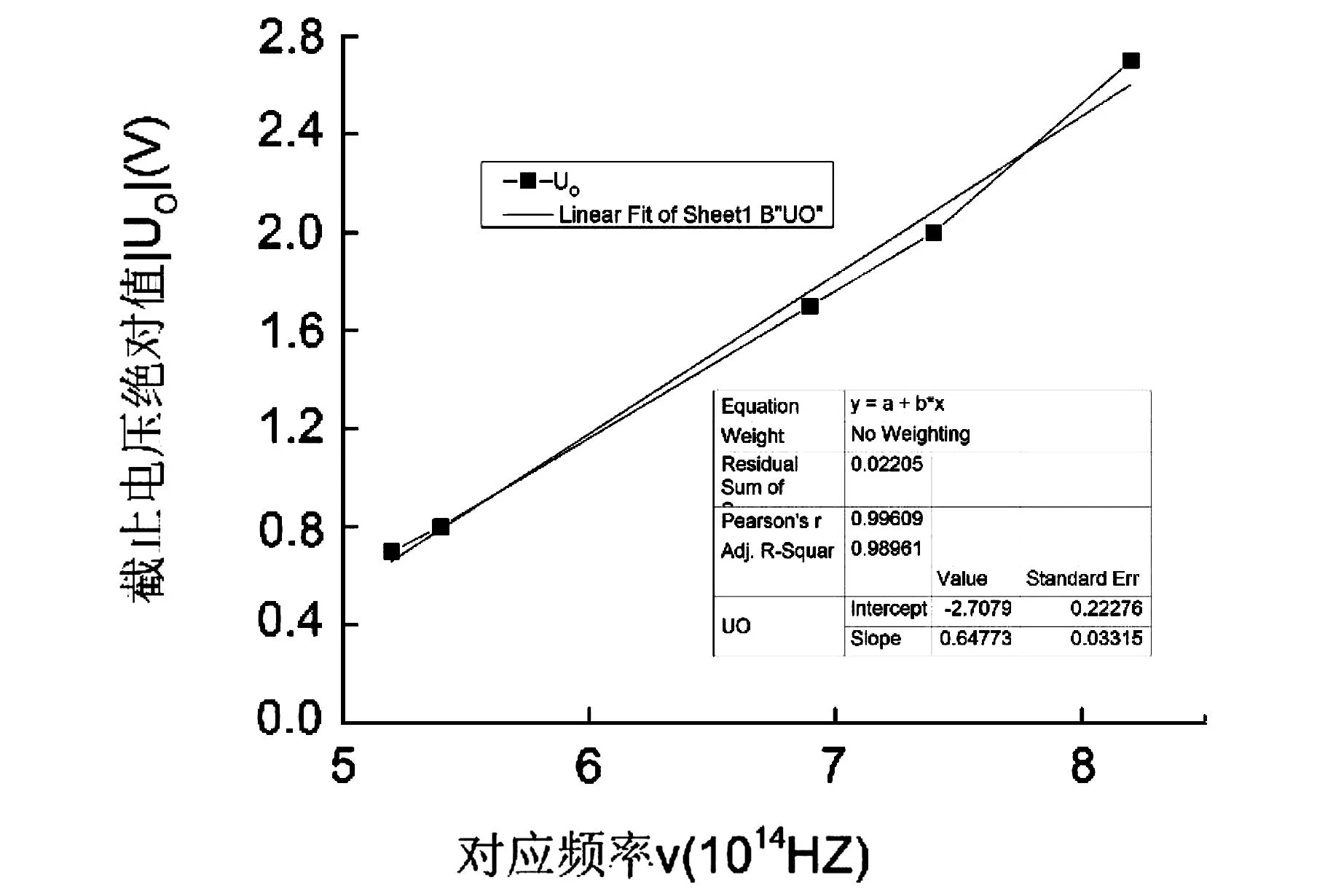
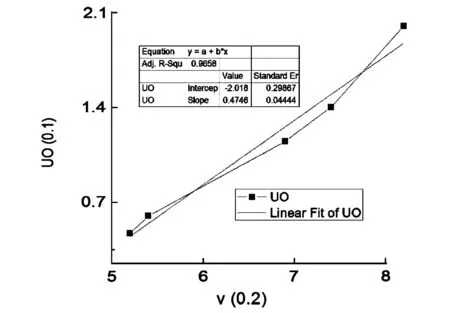
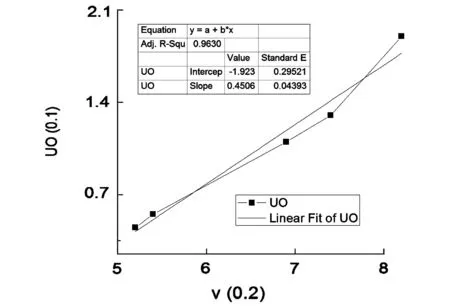
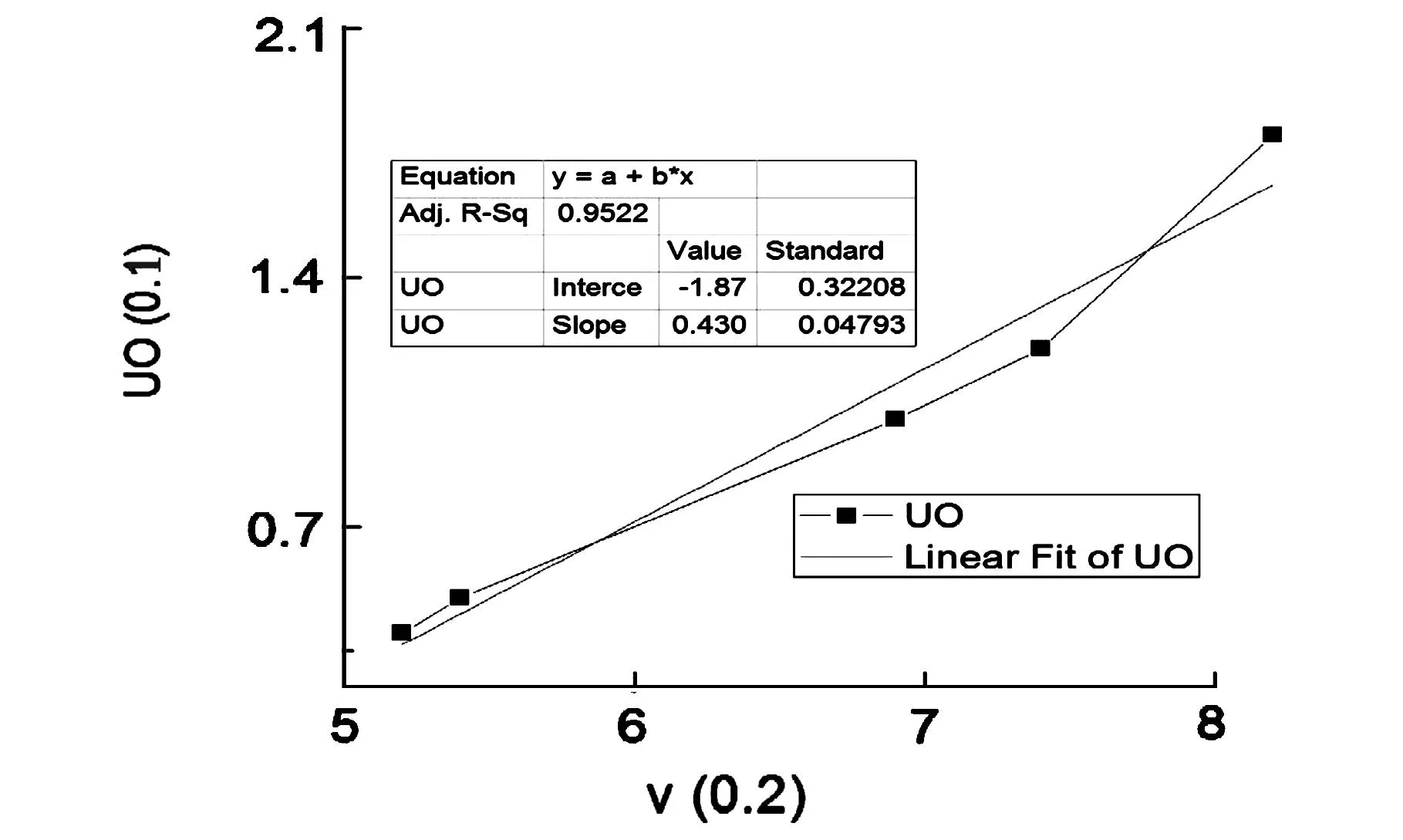
光子的能量hν

(2)式代入(1)式可得: eU0=hν-A

(3)

此等式表面：截止电压U0是频率ν的线性函数，直线斜率ɑ=h/e，因此只要用实验方法得出不同的频率对应的截止电压，求出直线斜率，就可以算出普朗克常数。

2实验内容

将电压选择按键置于-3—+20 V档。将滤色片旋转365.0 nm。调光阑到8 nm档。从低到高调节电压，精细地记录电流从非零到零点所对应的电压值，之后电压每变化一定值记录相应的电流值。再依次换上404.7 nm、435.8、546.1 nm、577.0的滤色片，重复以上测量步骤。绘制光电管的伏安特性曲线(电压调节范围在-3V~0 V)。

图2　5种频率光照射光电管的伏安特性曲线

根据画出的伏安特性曲线图中分别找出每条谱线的“截止电压”，此时涉及到“截止电压”的读取，不同的选取拐点会得到大小不一的结果，分析如下：

2.1选择电压有稍微有变化的点作为“截止电压”，数据如下

波长/nm365.0404.07435.8546.1577.0对应频率/Hz8.2×10147.4×10146.9×10145.4×10145.2×1014截止电压/V-2.7-1.9-1.6-0.8-0.7

以记录的电压值的绝对值作纵坐标，以相应谱线的频率作横坐标作出五个点，用此五点作一条ν-Uo，对此曲线进行拟合，得出直线的斜率a,再由实验原理中的(3)式：

得普朗克常数

h=α×e

=0.647 73×10-14HZ×1.602×10-19C

=1.037 7×10-33J.S

图3　频率随截止电压的关系图

用测量出的值与理论值(ho=6.625×10-34J.S)求出相对误差

E=|h-ho|/ho×100%

=|1.037 7×10-33-6.625×10-34|/6.625×10-34×100%=55.47%

2.2选择曲线曲率最小的地方，数据如下

波长/nm365.0404.07435.8546.1577.0对应频率/Hz8.2×10147.4×10146.9×10145.4×10145.2×1014截止电压/V-2.2-1.5-1.25-0.65-0.57

得到拟合后的ν-Uo。如图此时的普朗克常数

图4　曲率最小时ν与Uo的关系

h=α×e=0.507 4×10-14HZ×1.602×10-19C=0.812 85×10-33J.S

用测量出的值与理论值(ho=6.625×10-34J.S)求出相对误差

E=|h-ho|/ho×100%

=|0.812 85×10-33-6.625×10-34|/6.625×10-34×100%

=22.694%

2.3选择曲线有明显直线上升的点，数据如下

波长/nm365.0404.07435.8546.1577.0对应频率/Hz8.2×10147.4×10146.9×10145.4×10145.2×1014截止电压/V-2.0-1.4-1.15-0.6-0.47

此时得到拟合后的ν-Uo图像如图

图5　曲率较大时ν与Uo的关系

此时的普朗克常数

h=α×e

=0.474 6×10-14HZ×1.602×10-19C

=0.760 3×10-33J.S

用测量出的值与理论值(ho=6.625×10-34J.S)求出相对误差

E=|h-ho|/ho×100%

=|0.760 3×10-33-6.625×10-34|/6.625×10-34×100%=14.762 2%

2.4选直线上升一小段的点，数据如下

波长/nm365.0404.07435.8546.1577.0对应频率/Hz8.2×10147.4×10146.9×10145.4×10145.2×1014截止电压/V-1.9-1.3-1.10-0.55-0.45

此时得到拟合后的曲线ν-Uo图像如图

图6　拟合后ν与Uo的关系

此时普朗克常数

h=α×e

=0.450 6×10-14HZ×1.602×10-19C

=0.721 86×10-33J.S

用测量出的值与理论值(ho=6.625×10-34J.S)求出相对误差

E=|h-ho|/ho×100%

=|0.721 86×10-33-6.625×10-34|/6.625×10-34×100%=8.96%

2.5选直线上升靠后的点作为拐点，数据如下

波长/nm365.0404.07435.8546.1577.0对应频率/Hz8.2×10147.4×10146.9×10145.4×10145.2×1014截止电压/V-1.8-1.2-1.0-0.5-0.4

此时得到拟合后的曲线ν-Uo图像如图

图7　v与Uo的关系

此时的普朗克常数

h=α×e

=0.43×10-14HZ×1.602×10-19C

=0.688 86×10-33J.S

用测量出的值与理论值(ho=6.625×10-34J.S)求出相对误差

E=|h-ho|/ho×100%

=|0.688 86×10-33-6.625×10-34|/6.625×10-34×100%=3.978 8%

3结论

由以上5次取不同的“拐点”，得到的实验值相对于理论值的误差都在进一步减小。因此得出：在光电效应试验中，运用简单粗略的“拐点法”求普朗克常量时，应尽可能的把拐点确定在曲线变为直线上升后的点，即可使实验测出的普朗克常量趋近于理论值。

参考文献：

[1]闻春敖，郑晓东.光电效应法测量普朗克常数的数据处理及误差分析[J].光学技术，2009,12(35)：191-193．

[2]周永军，朴林鹤，吕佳.光电效应中测量普朗克的几种方法讨论[J].沈阳航空航天大学学报，2011，4(28)：85-87.

[3]王栋，等.基于Matlab光电效的测量光速的新方法研究[J].大学物理实验，2014(4)：12-13.

[4]陈小凡.光电效应实验中伏安特性曲线[J].大学物理实验，2014(3)：22-23.

The Method to Deal with the Large Error of Planck's Constant Error by the Method of "Inflection Point Method"

HUANG An-liang,XU Ping-chuan,CHEN Jin-jing

(China West Normal University,Sichuan Nanchong 637009)

Abstract：Using a simple "inflection point method" can quickly calculate Planck constant from the characteristic curve obtained by the photoelectric effect test,but the numerical error is relatively large,as to the error,the author carried out multiple times of the value analysis and calculation,and finally concluded the method to confirm the appropriate "point".

Key words：photoelectric effect；Planck constant；inflection point method；error

中图分类号：O 4-33

文献标志码：A

DOI：10.14139/j.cnki.cn22-1228.2016.001.027

文章编号：1007-2934(2016)01-0104-04

基金项目：西华师范大学基础课改专项(JCKGYB1414)；四川省教育厅科研项目(12ZB324)

收稿日期：2015-07-31