动态法测杨氏模量实验的探索与改进

樊聪聪，刘华扬，程敏熙

(华南师范大学，广东 广州　510006)



动态法测杨氏模量实验的探索与改进

樊聪聪，刘华扬，程敏熙

(华南师范大学，广东 广州510006)

摘 要：本文的主要工作有：分析了国内外杨氏模量测量的原理与方法；把测量装置由悬挂法改为支撑法，增加了实验棒的长度(原实验棒长度16 cm，新实验棒长度 23 cm),扩大了数据的测量范围；移动支架置于导轨上，可直接在导轨标尺上准确读数，每隔3 mm测一次数据，数据增多；组装调试实验装置，测量了黄铜、纯铜、钛三种材料的杨氏模量并进行数据处理，将改进后实验系统测得的结果和原实验系统测得的结果以公认值进行比较， 完善了改进后实验系统的教学功能。

关键词：杨氏模量；动态悬挂法；动态支撑法教学效果

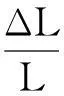
1杨氏模量实验方法

测量固体材料的杨氏模量也是理工科院校必做的大学物理实验之一，现阶段高校中测量杨氏模量的方法主要有静态拉伸法、梁弯曲法和动力学共振法。此外，也有很多学者研究了测量材料杨氏模量的新方法，如超声波法、霍尔传感器法、惠斯登电桥法、电容传感器法等等[2]。本文研究的是改进动态共振法测杨氏模量的实验装置，动态法测杨氏模量实验由清华大学现代应用物理学系丁慎训教授等人开发[3]，目前已广泛应用于高校的普通物理实验教学。通过查阅近年来国内外大量文献，笔者发现，研究动态法测杨氏模量的论文方向主要集中于数据的采集和处理及实验条件的控制等方面，对实验装置的整体改进和实验棒规格的控制，关注不够。笔者在长期接触该实验后，发现该实验在以下几个方面还存在改进空间：

1.1实验采用悬挂法存在弊端

该实验中调节悬挂点位置是靠手动调节，需要同时调节悬挂点和悬线在棒的位置，操作繁琐读数也不方便，且难以保持悬线始终处于竖直状态；激振器换能器输出、拾振器换能器接收的振动信号都需要经由悬线传送，实验棒振动会带动悬线摆动，会发生棒的变形及接触面绕其中心轴转动，悬线对棒也会有阻尼作用；拾取器要拾取的是加速度信号，但棒被悬在空中会发生摆动，有一部分摆动信号会被拾取；实验时仪器振动会影响自身的平衡性，这会影响棒发生共振的频率。

1.2通过外延法来确定棒的固有频率

由于实验棒比较短(约16 cm)，采集的数据点过少，造成实验描绘的悬挂点位置和发生共振频率关系的f-X曲线曲率不高，难以确定共振频率的最小值，因此可以对实验对棒的规格进行改进，增加其长度。

1.3实验中悬挂点的位置每次改变5 mm 测一次共振频率，间隔较大

当间隔比较大时，测量的精确度会降低，影响实验曲线的拟合。还有，实验读数时直接读实验棒上的标度，棒的标度通过手工标注，这样会造成比较大的误差。

笔者综合动态法测杨氏模量的实验原理和实验装置特点， 实验装置进行一定程度上的改进，以期使学生熟练实验的操作过程，提高实验效率，加深对实验原理的理解，达到实验的目的。

2对上述问题的改进

基于研究所发现的问题， 本文设计的动态法测杨氏模量实验装置改进的主要内容如下:

(1)实验装置的改进。实验中将实验棒的规格由L=16 cm，d=6 mm，改成L=23 cm，d=6 mm。将实验装置由悬挂法改为支撑法,将移动支架置于导轨上，在导轨上直接进行读数；为保持实验过程中的平衡，在激振器和拾取器下面加入平衡控制装置(如图1)。

图1　改进后实验装置示意图

(2)编写配合实验教学的指导方法，对实验系统进行改善，提出动态支撑法测杨氏模量实验的建议。

3动态法测杨氏模量实验的原理和装置

3.1受迫振动原理[4]

振动系统在连续的周期性外力作用下进行的振动叫做受迫振动， 根据牛顿第二定律，受迫振动的动力学方程为：

(1)

3.2实验原理分析

一细长棒(长度比横向尺寸大很多)的横振动(又称弯曲振动)满足动力学方程[5-6]

(2)

棒的轴线沿x方向，见图2，(2)式中η为棒上距左端x处横截面的z方向位移，Y为该棒的杨氏模量,ρ为材料密度，s为棒的横截面积,I为某一截面的惯量矩。

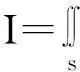
(3)

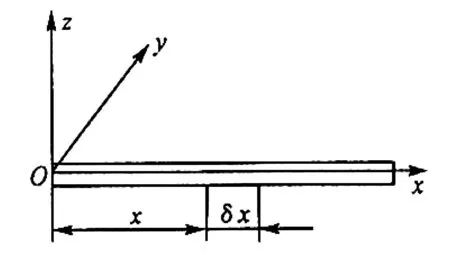
图2　细长棒的弯曲振动

用分离变量法(separation of variables)求解该方程。

(4)

式(4)称为频率公式，它对任意形状的截面试样，不同的边界条件下都是成立的。我们只要根据特定的边界条件定出常数K代入特定截面的惯量矩I就可以得出具体条件下的关系式。

对于长为L两端自由的棒，当悬线悬挂于棒的节点附近时，并且棒的两端均处于自由状态，那么在两端面上，横向作用力与弯曲矩均为零。

将边界条件代入通解得超越方程

cos(KL)ch(KL)=1

(5)

用数值计算法得到方程的根，依次是：

KnL=0，4.7300，7.853 2，10.995 6，14.137，17.279，20.420,…

(6)

上述第一个根“0”相应于静止状态，第二个根记为K1L=4.7300,与此相应的振动频率称为基振频率(或称固有频率)。

棒的横振动节点与振动级次有关，当n为第 1、3、5 等时，对应于对称形振动。当n为第 2、4、6 等时，对应于反对称形振动。图3给出了当n=1,2,3,4时的振动波形。

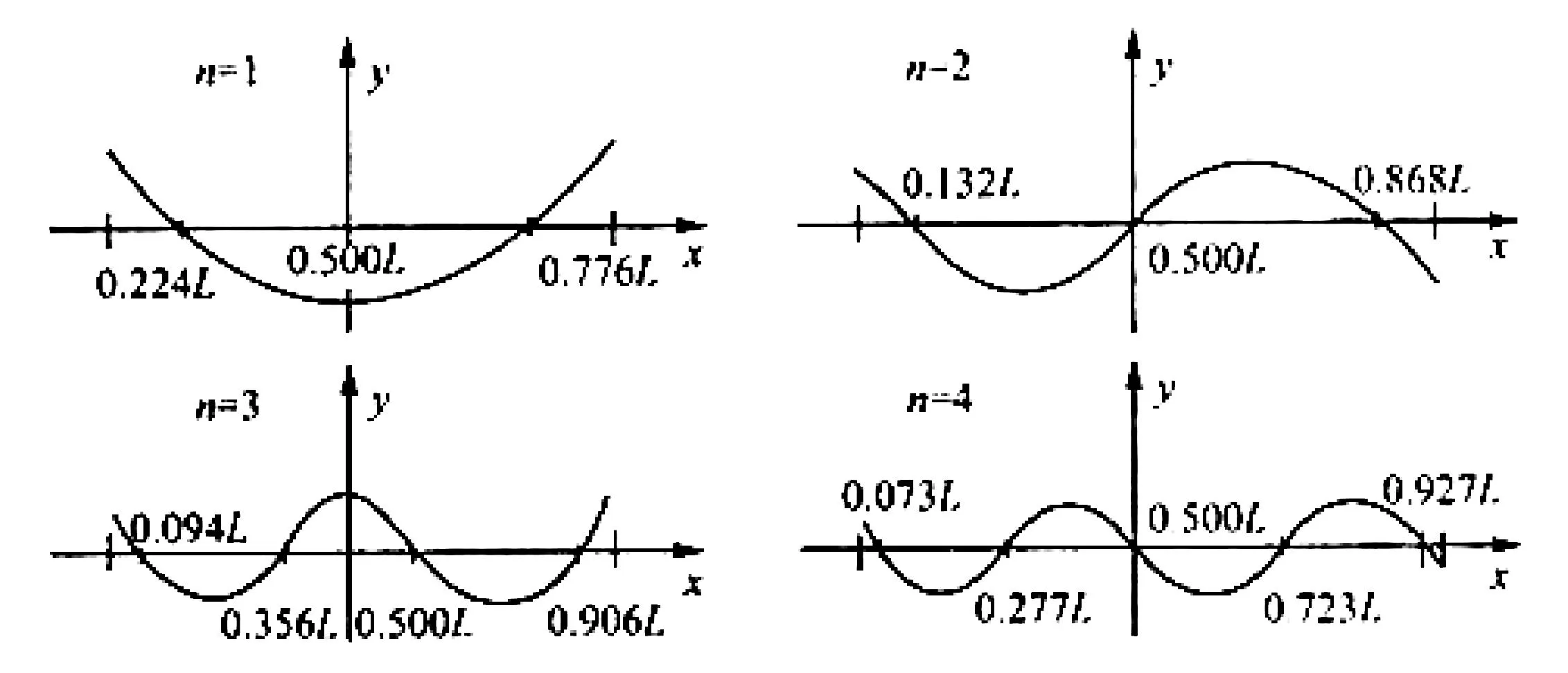
图3　棒的自由端振动波形

由n=1的图可以看出，试样棒在作基频振动时存在两个节点，它们的位置距离端面 0.224 L(距离另一端面为 0.776 L)处。理论上悬挂点应取在节点处，但由于悬挂在节点处试样棒难于被激振和拾振，为此，可在节点两旁选不同点对称悬挂，用外延法找出节点处的共振频率。

将第一个K1L=4.7300的K值代入式(2-4)，得到棒作为基频振动的固有频率为：

(7)

解出杨氏模量：

(8)

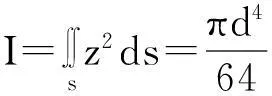
(9)

3.3动态法测杨氏模量实验装置系统

原实验系统(图4、5、6)由频率连续可调的音频信号源输出正弦电信号，经激振换能器转换为同频率的机械振动，由悬线把机械振动传给试样棒，试样棒作受迫振动， 同时其另一端的悬线再把试样棒的机械振动传给拾振换能器，这时机械振动又转变成电信号，信号经选频放大器的滤波放大，至示波器显示。当信号源频率不等于试样棒的固有频率时，试样棒不发生共振，示波器上几乎没有电信号波形或波形很小。当信号源的频率等于试样棒的固有频率时，试样棒发生共振，示波器上的波形突然增大，这时频率显示窗口显示的频率就是试样在该温度下的共振频率，代入即可计算该温度下的杨氏模量[7]。

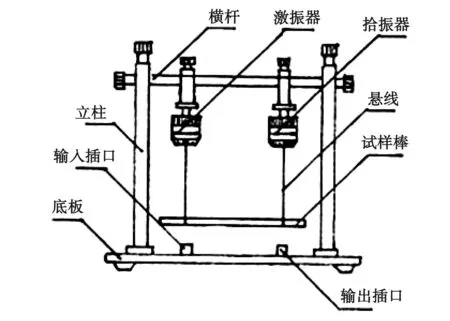
图4　FB209型动态杨氏模量测试仪结构图

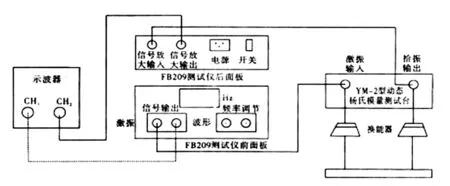
图5　FB209 型动态杨氏模量测试仪连接图

4实验系统的改进和实验数据分析

4.1实验系统的改进

本文对原动态法测杨氏模量实验系统做了较大改进，包括对整个实验装置的重新设计以及改进实验棒的规格。原实验装置采用的是悬挂法，为了克服其弊端，实验装置由悬挂法改为支撑法原实验系统测量不同数据点时需同时调节换能器和悬线在实验棒的位置，且实验棒的刻度直接用笔描出，既繁琐又不够准确，为了更好的读数，将移动支架置于导轨上，可直接在导轨上进行读数；为保持实验过程中的平衡，在激振器和拾取器下面加入平衡控制装置(图6，图7，图8，图9)。

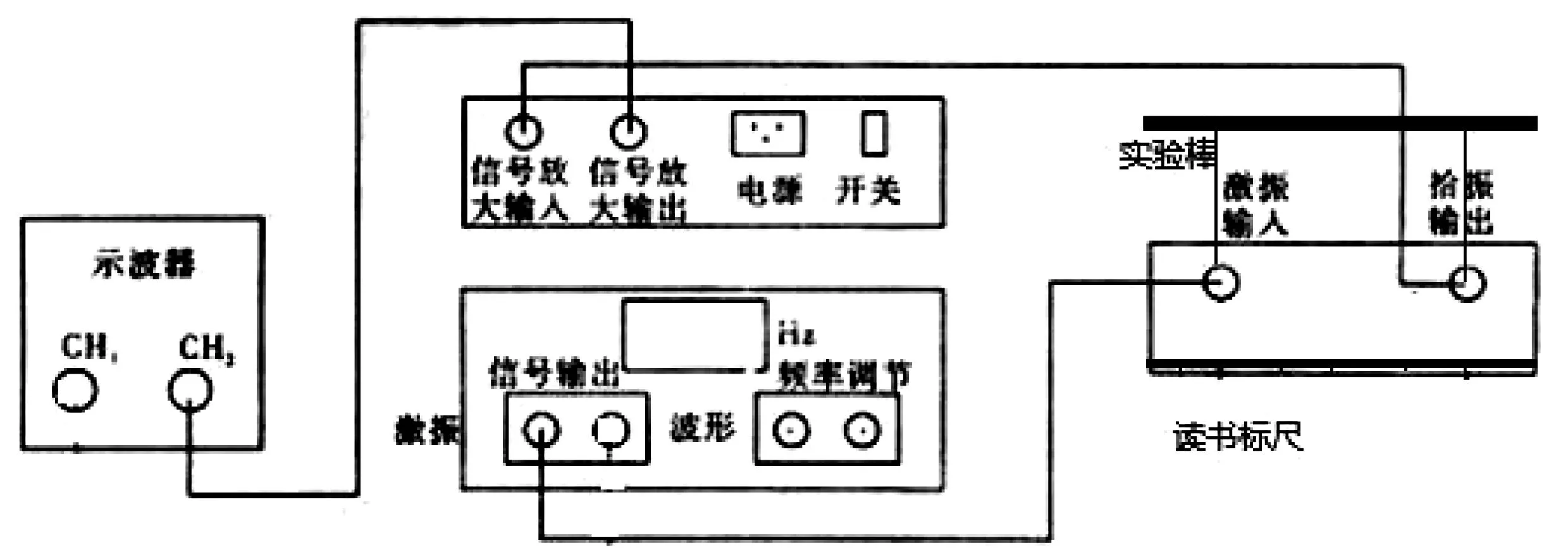
图6　改进后动态杨氏模量实验装置示意图

图7　改进前后实验棒规格

图8　改进前后读数方式对比

图9　改进后动态杨氏模量实验装置实物图

4.2实验方案

测试改进后实验装置的性能用改进后实验装置和原实验装置分别测试黄铜棒、纯铜棒、钛棒三种材料的杨氏模量，查询相关资料找到三种材料杨氏模量的理论值，计算用两种实验装置测得数据的相对误差，做出比较并得出结论。

4.2.1改进后黄铜棒实验分析及比较

用改进后实验系统测量黄铜棒的杨氏模量，表1是在不同的支撑点x测得的共振频率f的数据，表2是改进黄铜棒的规格数据(L、d、m分别是黄铜棒的长度、直径和质量)。

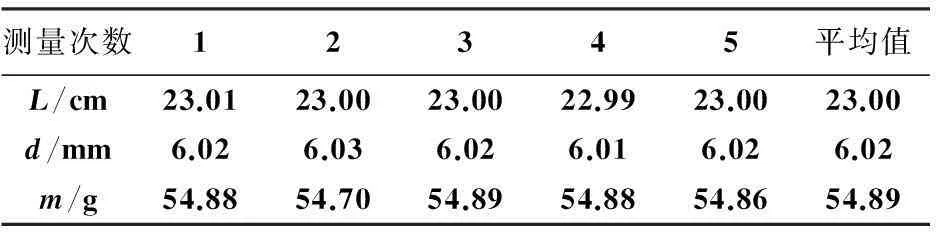
表1　改进后黄铜棒规格参数

表2　改进后实验系统黄铜棒实验数据

根据表1数据，用matlab软件描点拟合作f-x图，并利用软件寻找出最小频率点，如图10所示：

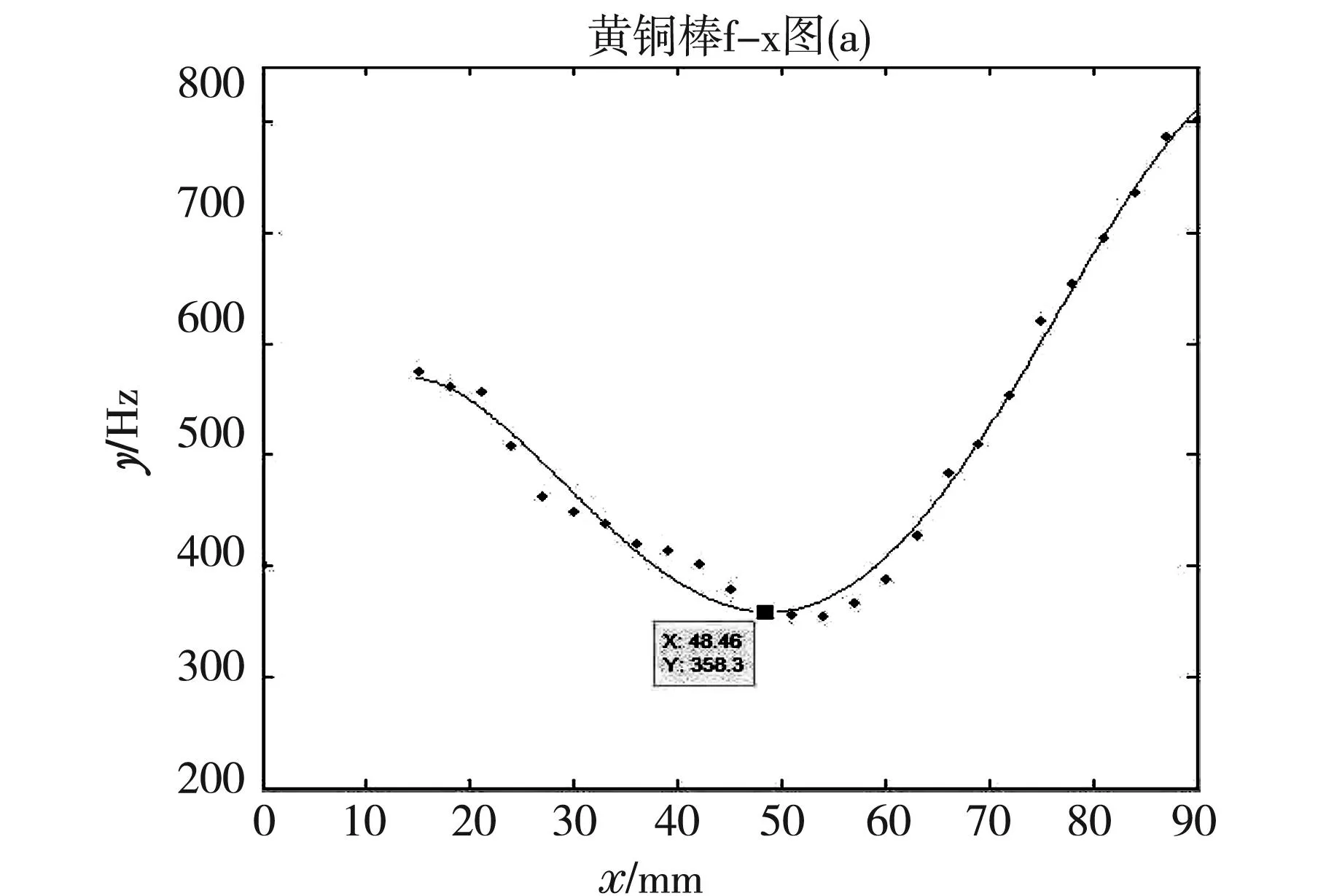
图10　改进后实验系统黄铜棒f-x图

从图中可以看到曲线最低点的频率f=358.3 Hz，代入杨氏模量的计算公式可得:

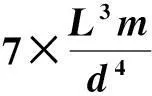
通过查阅资料可知常温下黄铜棒(Cu70 Zn30,ρ=8.45 g/cm3)的杨氏模量公认值为：Y=1.05×1011(N/m2)，改进后实验系统测得的相对误差为9.5%。

4.2.2原黄铜棒实验分析及比较

用原实验系统测黄铜棒的杨氏模量，表3是在不同的悬挂x测得的共振频率f的数据，表4是原黄铜棒的规格数据。

表3　原实验系统黄铜棒f-x图

表4　原实验系统黄铜棒参数

根据表4数据，用matlab软件描点拟合作f-x图，并利用软件寻找出最小频率点，如图11所示。

图11　原实验系统黄铜棒f-x图

从图中可得出曲线最低点的频率f=703.4 Hz，代入公式算得：

通过查阅资料可知常温下黄铜棒(Cu70 Zn30,ρ=8.45 g/cm3)的杨氏模量公认值为：Y=1.05×1011(N/m2)。

原实验系统测得的黄铜棒杨氏模量相对误差为：13%。

对比改进前后的测量结果可知，改进后实验系统的准确度比原实验系统高近4个百分点，可以看出在黄铜棒的测量上使用改进后实验系统还是比较理想的。

4.2.3改进后实验系统对纯铜棒实验分析

纯铜又名红铜即铜单质，表5是在不同的支撑点x测得的共振频率f的数据，表6是改进后纯铜棒的规格数据(L、d、m分别是纯铜棒的长度、直径和质量)。

表5　改进后实验系统纯铜棒实验数据

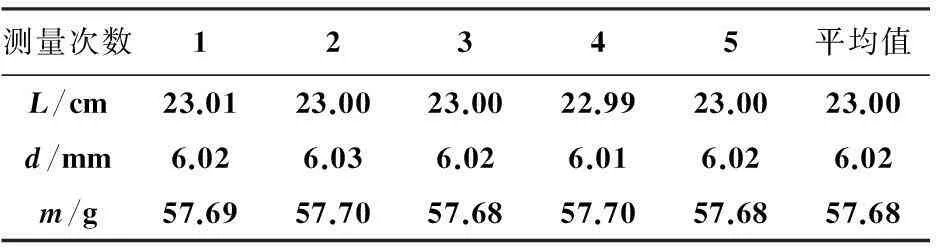
表6　改进后实验纯铜棒规格参数

根据表5数据，用 matlab 软件描点拟合作f-x 图，并利用软件寻找出最小频率点，如图12所示：

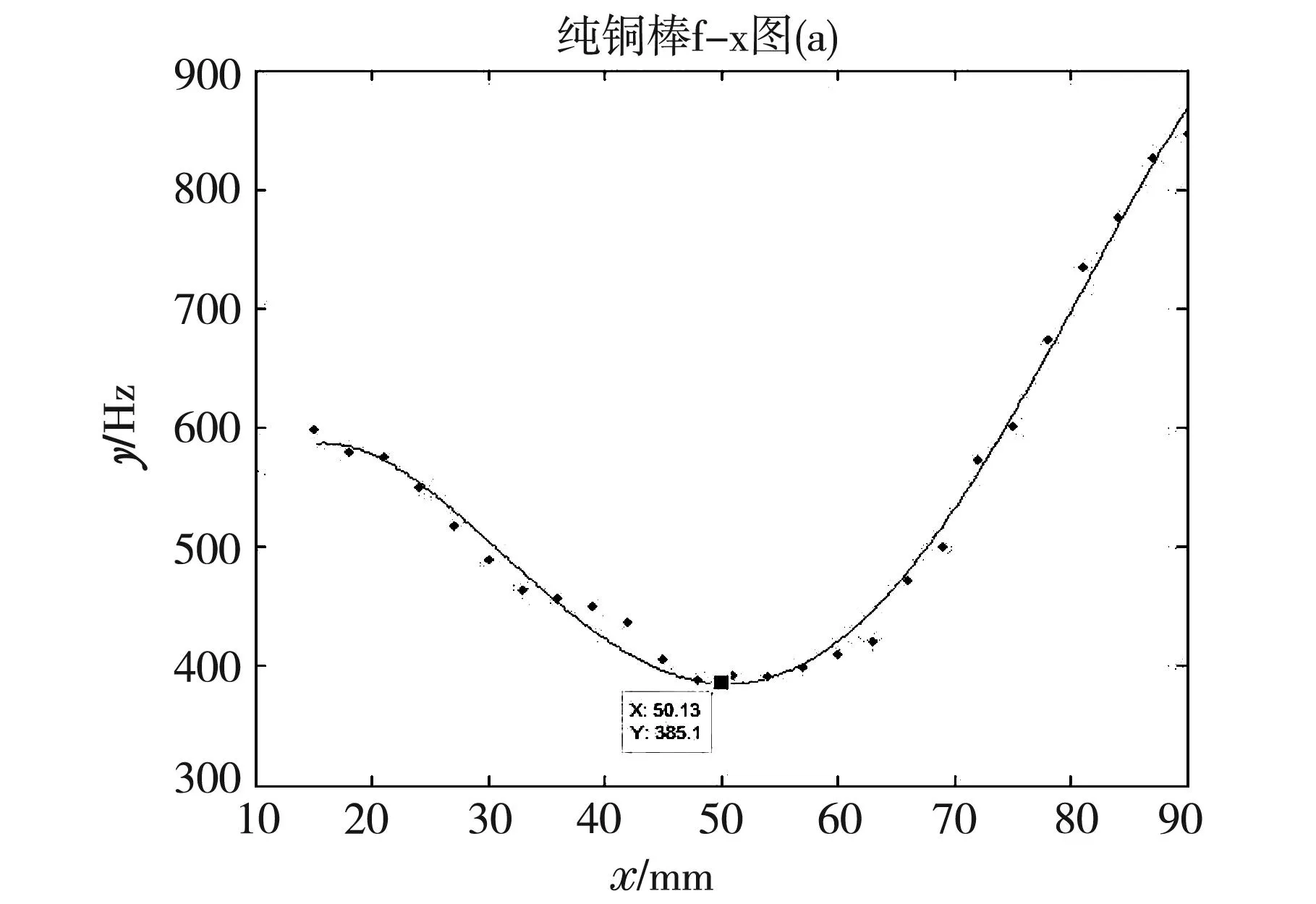
图12　改进后实验系统纯铜棒f-x图

从图中可以看到曲线最低点的频率f=385.1 Hz，代入杨氏模量的计算公式可得：

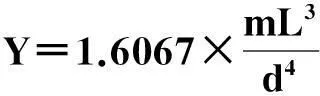
4.2.4原实验系统纯铜棒实验分析及比较

用实验系统测量纯铜棒的杨氏模量。表7是在不同的悬挂x测得的共振频率f的数据，表8原实验纯铜棒的规格数据(L、d、m分别是纯铜棒的长度、直径和质量)。

表7　原实验系统纯铜棒实验数据

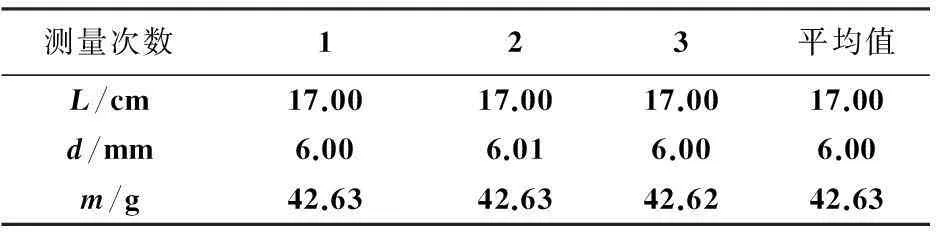
表8　原实验纯铜棒规格参数

根据表7数据，用matlab软件描点拟合作f-x图，并利用软件寻找出最小频率点，如图13所示：

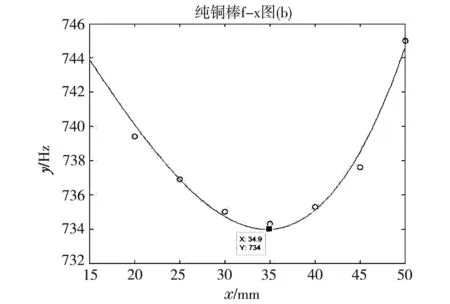
图13　原实验系统纯铜棒f-x图

图中可得出曲线最低点的频率f=734.0 Hz，代入公式算得：

通过资料查询可知常温下纯铜的杨氏模量公认值为：

Y=1.22×1011(N/m2)

故改进后实验系统测得纯铜棒杨氏模量的相对误差：

原实验系统测得的纯铜棒杨氏模量相对误差：

计算结果显示，改进后实验系统测得的相对误差为5.8%，原实验系统测得的相对误差为12%，使用改进后的实验系统测量纯铜棒的杨氏模量误差明显更小，测量更准确。

4.2.5钛棒实验分析及比较

用改进后实验系统测量钛棒的杨氏模量。表9是在不同的支撑点x测得的共振频率f的数据，表10是改进后钛棒的规格数据。

表9　改进后钛棒规格参数

表10　改进后实验系统钛棒实验数据

根据表10数据，用matlab软件描点拟合作f-x图，并利用软件寻找出最小频率点，如图14所示。

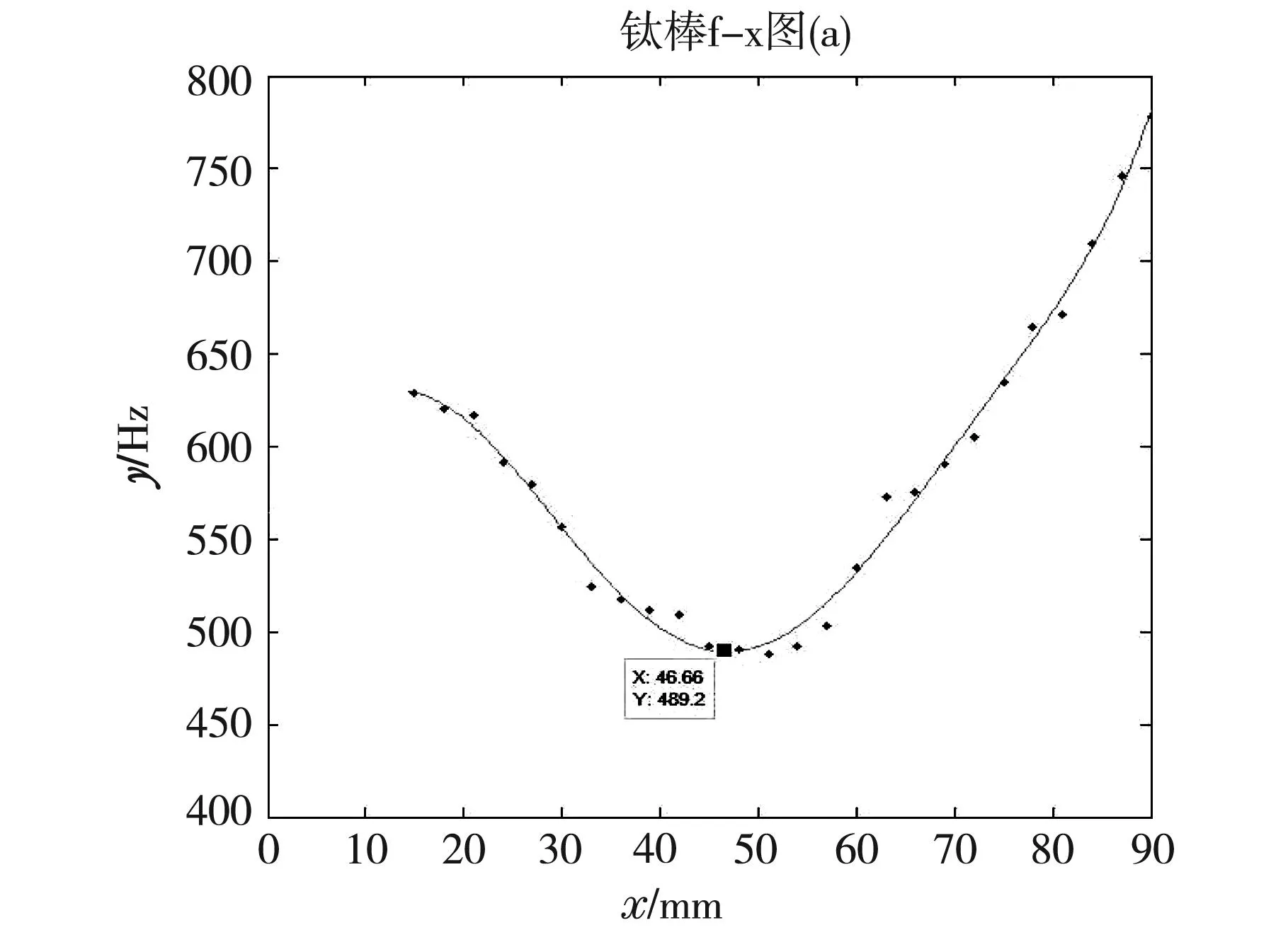
图14　改进后实验系统钛棒f-x图

从图中可以看到曲线最低点的频率f=489.2 Hz，代入杨氏模量的计算公式可得：

4.2.6原实验系统钛棒实验分析

用原实验系统测钛棒的杨氏模量，表11是在不同的悬挂x测得的共振频率f的数据，表12是原钛棒的规格数据(L、d、m分别是钛棒的长度、直径和质量)。

表11　原实验系统钛棒实验数据

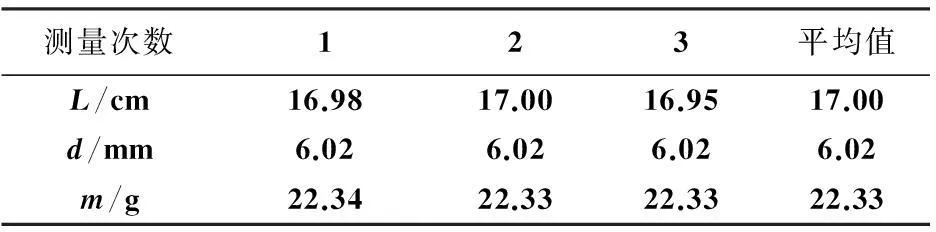
表12　原实验钛棒规格参数

根据表12数据，用matlab软件描点拟合作f-x图，并利用软件寻找出最小频率点，如图15所示。

图15　原实验系统钛棒f-x图

图中可得出曲线最低点的频率f=988.4 Hz，代入公式算得

常温下钛的杨氏模量公认值为

Y=1.16×1011(N/m2)

故改进后实验系统测得钛棒杨氏模量的相对误差：

原实验系统测得的钛棒杨氏模量相对误差：

由以上可以看出，改进后实验系统测得的钛棒杨氏模量相对误差为8%，原实验系统测得的钛棒杨氏模量相对误差为13%，改进后的实验系统准确度更高一些。

5实验结果分析

使用改进后的实验装置对三种不同材料杨氏模量的测量，以纯铜棒为例，通过查阅相关文献，很多学者研究此实验使用的材料均是纯铜棒，测得的纯铜棒杨氏模量大多在(1.05～1.35)×1011(N/m2)之间，如开发者丁慎训教授测得的实验结果为1.14×1011(N/m2)，相对误差为 6.6%[8]，华南理工大学徐嘉彬测得的实验结果为.13×1011(N/m2)，相对误差为7.4%[9]，装甲兵工程学院季诚响的实验结果为1.12×1011(N/m2)，相对误差为8.2%[10-36]，本文使用改进后实验装置测得的实验结果为1.29×1011(N/m2)，相对误差为5.8%，因此可以认为使用改进后的实验装置在纯铜棒的测量上取得了较好的实验效果。 通过比较分析，改进后实验装置和原实验装置的测量结果的相对误差均在10%左右，都具有比较高的精确度，改进后实验装置在测量黄铜棒、纯铜棒、钛棒时实验误差均比原实验装置更为准确，达到了较为理想的实验效果。改进后的实验系统在操作的便捷性上远胜原实验装置，且读数和调节都更为方便，使用改进后的实验装置还是有很大的优势。

参考文献：

[1]王惜宝.材料加工物理[M].天津：天津大学出版社，2011.

[2]田莳.材料物理性能[M].北京：北京航空航天大学出版社，2007(8).

[3]周晓明.三种杨氏模量测量方法比较[J].实验科学与技术，2011(12).

[4]石大庆，江超,等.CCD杨氏模量测量仪的实验研究[J].实验科学与技术，2010(10).

[5]彭涛，王新春，王宇,等.电桥法测杨氏模量的实验研究[J].大学物理实验，2011(2).

[6]魏勤，卫婷,董师润,等.超声波法测量金属材料的杨氏模量和剪切模量[J].江苏科技大 学学报，2012(2).

[7]徐嘉彬,袁海甘,等.弯曲共振法测量材料的杨氏模量实验改进[J].物理实验，2011(11).

[8]丁慎训,傅敏学,丁小东,等.用动力学法测杨氏模量实验及其实验装置的研制[J].大学物 理，1999(7).

[9]余观夏，张爱珍，阮锡根.用共振法测定动态杨氏模量实验装置的改进[J].物理实验，2004(2).

[10] 张卫华,阿继凯.动态法测金属杨氏模量实验的研究[J].青海大学学报，2006(4).

[11] 吴阳明,朱祥.动态法测金属杨氏模量的理论研究[J].大学物理，2009(3).

[12] 陈映纯，吴先球.基于虚拟仪器的杨氏模量实验中共振频率的测量[J].物理实验，2012(5).

[13] 漆安慎，杜禅英著.力学[M].北京：高等教育出版社，2005.

[14] 赵凯华。新概念物理教程.力学[M].北京：高等教育出版社，2004.

[15] 王华，任明放，等.大学物理实验[M].广州：华南理工大学出版社，2008.

[16] 同济大学应用数学系，高等数学[M].北京：高等教育出版社，2001.

[17] 王华，任明放，等.大学物理实验[M].广州：华南理工大学出版社，2008.

[18] {日}饭田修一，大野和郎.物理学常用数表[M].北京：科学出版社，1969.

[19] C.诺德林，J 奥斯特曼.简明物理学手册[M].北京：科学出版社，1989.

[20] 王世敏.物理教学的任务[J].物理教学，2002.

[21] 杨维东.建构主义学习理论述评[J].理论导刊，2011(5).

[22] 李良霞.建构主义学习理论及其在物理教学实践上的研究[D].长沙：湖南师范大学硕士 学位论文，2004.

[23] 谢江阳.基于建构主义的物理教学.[J].教育信息化，2004.

[24] 崔宝金.中学物理教学中计算机辅助教学现状的调查和研究[D].北京：首都师范大学硕 士论文，2008.

[25] 郑静华，PPT 课件设计原则和实用技巧[J].中国教育技术装备，2011(26).

[26] 于丽华，陈爽.关于 CAI 课件制作的思考[J].辽宁师专学报，2003(2).

[27] 刘吉森,张进治.杨氏模量的动态法测量研究[J].北方工业大学学报，2006(3).

[28] 郑志远,樊振军,董爱国，等.动态法测材料杨氏模量中异常频率变化的测量研究[J].实验室科学，2011.

[29] 季诚响,丁晟.动态法测量杨氏模量实验的数据处理[J].实验室科学，2009(2).

[30] 段卓琦.金属杨氏模量的动态法测量研究[J].科技信息，2009(29).

[31] 张凡,姜伟,吕丹.关于动态法测量金属杨氏模量实验的两个重要方面的研究[J].大学物理实验，2007(12).

[32] 黄亦明.动态法测定材料的杨氏模量[J].物理与工程，2002(5).

[33] 何熙起.动态法测杨氏模量共振频率的拟合研究[J].内江师范学院学报，2010(10).

[34] 朱华，李翠云.动态法测金属杨氏模量实验中的谐振频率[J].物理实验，2004(7).

[34] 杨周琴.共振法测量金属材料的杨氏模量实验探讨[J].新课程：教育学术，2011(9).

[35] 张青兰，杨周琴.动态弹性模量测量中的谐振频率分析[J].大学物理实验，2010(8).

[36] 蒋毅，陈美华，等.测杨氏模量的一种新方法_驻波法[J].嘉应学院学报，2010(11).

Improvements of Measuring the Young's Modulus by Dynamic Method and Its Research on Teaching

FAN Song-song，LIU Hua-yang，CHENG Min-xi

(South China Normal University,Guangdong Guangzhou 510006)

Abstract：Its main content is analyzing the theories and methods of Young's modulus at home and abroad,increasing the length of experiment bar(original length is 16 cm,revised length is 23 cm),increasing the measure scale；installing mobile stand on the rail,measuring every 3 mm of rail rod,increasing the amount of data；setting up the experiment device,measuring and processing the Young’s modulus of brass,copper and titanium,comparing the results of revised experiment system,original experiment system and theoretical value；improving the teaching function of revised experiment system,compiling experiment guidance.

Key words：Young's modulus；dynamic suspension method；dynamic supporting method

中图分类号：O 4-33

文献标志码：A

DOI：10.14139/j.cnki.cn22-1228.2016.001.014

文章编号：1007-2934(2016)01-0051-09

收稿日期：2015-10-02