TBM盘形滚刀破岩数值模拟
张 禹 张延荣 辛 倩
(沈阳工业大学 机械工程学院,沈阳 110870)
TBM盘形滚刀破岩数值模拟
张 禹 张延荣 辛 倩
(沈阳工业大学 机械工程学院,沈阳 110870)
为研究切削深度和刃角对滚刀破岩的影响,以Mohr-Coulomb模型和岩石力学性质为基础,利用ABAQUS软件建立单把盘形滚刀破岩的三维有限元模型,实现对滚刀破岩过程的模拟,总结滚刀破岩机理。仿真结果表明,切削深度和刃角的变化对滚刀破岩影响均较明显;增大滚刀的切削深度会加速其磨损失效,选用小刃角滚刀破岩效率更高,刀具的磨损更小。
盘形滚刀 Mohr-Coulomb模型 数值模拟 切削深度 刃角
引言
先进轨道交通装备被《中国制造2025》规划列为十大重点支持、突破产业领域之一。岩石隧道掘进机作为先进轨道交通装备,具有对周围环境影响小、自动化程度高、施工快速、优质高效、安全环保等优点。盘形滚刀作为岩石隧道掘进机的关键部件,直接与岩石接触,因此,对盘形滚刀破岩进行三维有限元模拟,分析滚刀破岩机理,对改进滚刀结构,优化滚刀布局,进而提高施工效率具有重要的意义。
目前,国内外许多学者运用计算机仿真对滚刀破岩机理进行许多研究。谭青[1]等利用离散元方法建立岩石与盘形滚刀的二维数值模型,研究了滚刀侵入岩石过程中切削深度、切削力和裂纹数三者的关系;刘泉声[2]等通过分析滚刀运动规律,研究了滚刀法向推力对破岩的作用;张照煌[3]等通过考虑岩石的各向异性,深入研究岩石在盘形滚刀作用下的形变和剥落特点;高浩[4]等利用数值模拟对滚刀破岩过程进行分析,研究盘形滚刀破岩过程中刀圈接触应力分布规律。本文利用ABAQUS有限元软件,在Mohr-Coulomb准则和岩石力学性质的基础上,进行盘形滚刀破岩模拟仿真,研究不同刃角与切削深度对滚刀破岩的具体影响。
1 建立岩石破岩模型
1.1 理论模型
作为岩石力学中重要的强度理论之一,Mohr-Coulomb强度准则不仅可反映岩石的脆性破坏,且能反映其塑性破坏特征。Mohr-Coulomb模型的参数也可通过岩石三轴强度试验等常规试验获得。根据岩石的本构关系、破坏机理及其他物理力学性质,建立岩石的Mohr-Coulomb弹塑性模型用于模拟滚刀破岩。在模拟过程中,假定岩石在单轴条件下表现出典型的脆性破坏特征,其破坏机制在宏观上表现为剪切、在局部上表现为拉伸[5]。

Mohr-Coulomb屈服准则表达式:τf和σnf分别为屈服平面上的剪应力与压应力,c、φ是岩石参数,c为岩石的黏聚力,φ为岩石的内摩擦角。图1为摩尔应力圆,其中σ1=σv,σ3=σh。公式(1)也可表示为:
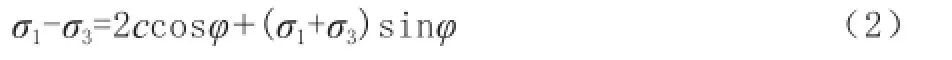
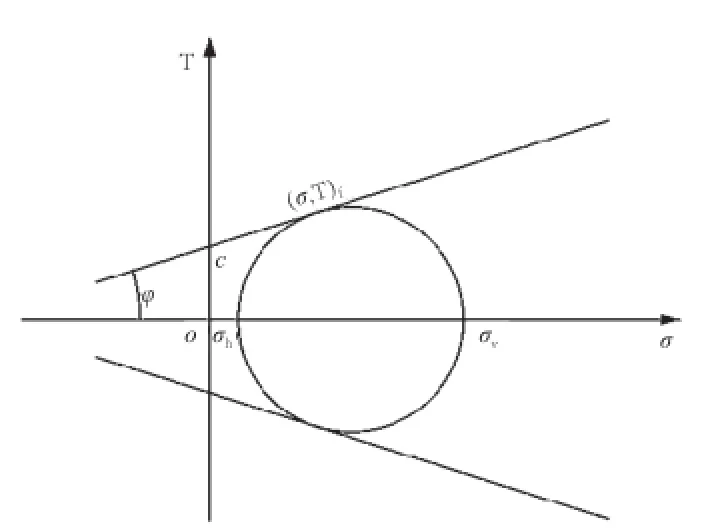
图1 Mohr-Coulomb屈服准则
公式(2)通常被称为Mohr-Coulomb失效准则,模型的屈服函数为:
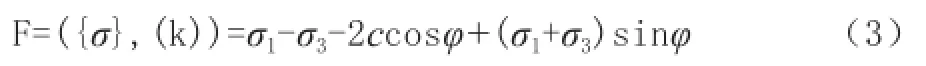
Mohr-Coulomb模型为理想塑性模型,主要适用于单调载荷下颗粒状材料。公式(3)中k为状态参数,假定其为恒量且独立于塑性应变与塑性功。根据Mohr-Coulomb破坏准则,当黏聚力c与有效压应力σnftanφ之和超过岩石的剪应力τf,即图1中某点的莫尔应力圆与库伦直线相割时,即发生剪切破坏[6],即破坏条件是:

1.2 三维数值模型
图2是滚刀破岩的三维数值模型,选用17英寸滚刀,17英寸滚刀较其他滚刀具有良好的使用性能、经济性、安装灵活等优点,因此在现代盾构施工中应用更广泛。滚刀刀圈直径为432mm,厚度为80mm,刃宽为12mm。岩石模型为长方体,尺寸为600mm×200mm×160mm。为研究刃角、切削深度对滚刀破岩的影响,分别选用刃角为20°、40°、60°与切削深度为3、5、7mm,共9组组合。

图2 三维数值模型
由于主要研究滚刀的破岩机理,因此在数值模拟过程中将滚刀设置为刚体,不考虑其变形。模型中岩石材料的参数见表1。岩石模型的网格如图2所示,采用八节点的缩减积分单元(C3D8R),共划分12000个网格单元。在模拟过程中,设置岩石的上表面为主动面,滚刀的外表面为从动面,约束岩石底面所有自由度,滚刀沿岩石上表面(Z轴)的速度为528mm/s,绕X轴的滚动速度为2π,模拟时间为1s。

表1 岩石材料参数
2 数值模拟结果分析
2.1 盘形滚刀破岩过程
滚刀的切削过程分为两个阶段:滚刀侵入岩体和相邻滚刀间的裂纹相互贯通[7]。首先,滚刀在径向推力作用下侵入岩体。刀刃下方岩石在推力作用下破碎,破碎的岩石在推力的持续作用下被压成密实核。随后,密实核将滚刀压力传递给周围岩石,随着滚刀的连续作用,相邻滚刀间的岩体裂纹继续扩展直到相互贯通,形成大块的岩石碎片,最终完成一次完整的破岩过程如图3所示。

图3 单把滚刀破岩的应力分布
2.2 仿真结果分析
图4、图5、图6分别是刃角为20°、40°、60°的滚刀在切削深度为3、5、7mm时切削岩石的仿真结果。岩石在滚刀的剪切,挤压作用下变形逐渐增大,首先发生弹性变形,随着受力的不断增大,进而发生塑性变形。当岩石所受的应力超过其最大屈服应力时,岩石破碎,即滚刀完成一次破岩过程。从图中可以看出岩石所受的应力随着切削深度的增加而不断变大,不同刃角的滚刀切削岩石,在相同的切削深度下岩石所受的应力也不相同。
假设剪切面为单一介质,岩石的极限抗剪切强度为常数[8],根据公式(5)近似给出的抗剪强度[9]:

其中c0为岩石单轴抗压强度,f为剪切面上的内摩擦系数,取c0=120MPa,φ=53°,计算得岩石的抗剪切强度τf≈36.11MPa。
如图4所示,滚刀的刃角为20°时,三个切削深度下岩石所受的最大剪切应力范围分别为29.57~32.52MPa, 35.47~45.67MPa,41.08~44.80MPa。从图5得出,滚刀刃角为40°时,三个切削深度下岩石所受的最大剪切应力分别为30.99~34.07MPa,34.88~37.16MPa,37.16~44.90MPa。如图6所示,滚刀刃角为60°时,三个切削深度下岩石所受的最大剪切应力范围分别为29.60~32.54MPa,32.53~35.47MPa,37.46~41.18MPa。
因而,根据公式(5)给出的剪切破坏条件,三种刃角的滚刀分别在5mm、5mm、7mm实现破岩。

图4 刃角为20°时岩石的Mises应力分布

图5 刃角为40°时岩石的Mises应力分布
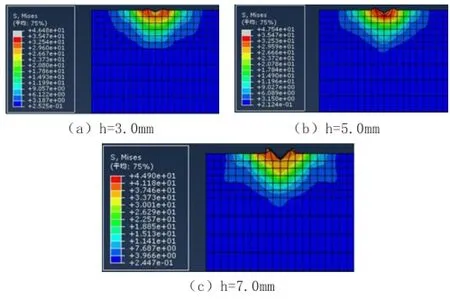
图6 刃角为60°时岩石的Mises应力分布
3 结语
(1)利用ABAQUS/Explicit分析模块,在Mohr-Coulomb模型和岩石力学性质的基础上,建立TBM盘形滚刀破岩的三维有限元模型。
(2)选取不同刃角的滚刀,分别在不同切削深度下进行滚刀破岩的数值仿真。结果表明切削深度一定的条件下,岩石所受的应力与刃角大小呈负相关;相同刃角的条件下,岩石所受的应力与切削深度呈正相关。
(3)研究滚刀破岩过程仿真结果,发现三种刃角的滚刀破岩深度分别为5mm、5mm、7mm,刃角小的滚刀破岩效率更高,磨损小,稳定性好在实际施工过程中,既要考虑施工效率,又要兼顾经济成本,因而选用较小刃角的滚刀更具优势。
[1]谭青,李建芳,夏毅敏,等.盘形滚刀破岩过程的数值研究[J].岩土力学,2013,34(9):2707-2714.
[2]刘泉声,时凯,朱元广,等.TBM盘形滚刀破岩力计算模型研究[J].煤炭学报,2013,38(7):1136-1142.
[3]张照煌,叶定海,袁昕.岩石在盘形滚刀作用下的性能研究[J].水利学报,2011,42(10):1247-1251.
[4]夏毅敏,欧阳涛,陈雷,等.盘形滚刀破岩力影响因素研究[J].应用基础与工程科学学报,2012,20(3):500-506.
[5]张帆.三峡花岗岩力学特性与本构关系研究[D].武汉:中国科学院武汉岩土力学研究所,2007:32-33.
[6]张义同,高健,乔金丽,等.隧道盾构掘进土力学[M].天津:天津大学出版社,2010:50-52.
[7]Lida Zhu,Jijiang Wu,Chunguang Liu,et al. Research on Simulation Process of Rock Broken by TBM Hob[J]. Advanced Materials Research,2013,(712-715):633-636.
[8]秦四清,王思敬,孙强,等.非线性岩土力学基础[M].北京:地质出版社,2008:34-35.
[9]李世愚,和泰名,尹祥础.岩石断裂力学导论[M].合肥:中国科学技术大学出版社,2010:256-266.
Numerical Simulation of Rock Cutting by TBM Disc Cutter
ZHANG Yu, ZHANG Yanrong, XIN Qian
(Shenyang University of Technology Institute of Mechanical Engineering, Shengyang 110870)
In order to investigate the influence caused by the change of the penetration depth and the blade angle of the disc cutter, the three-dimensional finite element model was established in ABAQUS software. The rock broken process was simulated and the mechanism of rock fragmentation was summarized. It could be found that remarkable influence was caused by the change of the penetration depth and the blade angle of the disc cutter. The wearout failure could be accelerated by the increase of the penetration depth of the disc cutter. Much more efficiency and small tool wear would be occurred after choosing small blade angle.
disc cutter, Mohr-Coulomb model, numerical simulation, penetration depth, blade angle

