基于自适应神经模糊推理系统和灰色理论的机床热误差补偿研究*

丁群燕 曾 鑫

(①武汉软件工程职业学院电子工程学院，湖北 武汉 430205； ②武汉软件工程职业学院汽车工程学院，湖北 武汉 430205)

基于自适应神经模糊推理系统和灰色理论的机床热误差补偿研究*

丁群燕①曾 鑫②

(①武汉软件工程职业学院电子工程学院，湖北 武汉 430205； ②武汉软件工程职业学院汽车工程学院，湖北 武汉 430205)

提出了自适应神经模糊推理系统(ANFIS)模型，采用灰色理论对机床热误差进行建模，实现机床加工工件定位误差值的最小化。采用自适应模糊推理系统的模糊C均值聚类法，对机床上的温度传感器进行聚类分组和分析，选择出每组最优的温度传感器，将测量温度传感器从76个减少到5个。提出了灰色系统理论，对GM(1，N)公式进行了推导，创建了热误差预测模型。采用实验测量方法对机床运行所产生的误差进行了验证。实验结果显示：补偿前Y轴和Z轴产生热误差的最大值分别为41.5 μm和33.8 μm，补偿后Y轴和Z轴产生热误差的最大值分别为4.8 μm和4.6 μm。采用自适应神经模糊推理和灰色系统对机床热误差进行补偿，不仅测量温度传感器数量减少，而且机床主轴运行所产生的误差明显减小，加工精度较高，效果很好。

数控机床；自适应模糊推理系统；模糊C均值聚类法；灰色理论；热误差补偿

随着科学技术的进步，机械加工产业也在向着高精度方向发展。高精度是机械产品竞争能力的主要因素，特别是生产制造机械。伴随超精密产品的诞生，对机床的加工精度要求也会越来越高。通常情况下，数控机床运行过程中产生的误差包括以下几个部分：(1)机床热变形产生的误差；(2)切削力产生的误差；(3)刀具磨损产生的误差；(4)机床定位误差等等。在机床运行所产生的多种误差中，机床的热误差是占据主导地位[1]，大约占总误差的70%。因此，必须尽快降低机床热误差的影响，提高机械零部件的生产精度。

当前，主要是通过两种方法减小机床热误差的影响，分别为误差防止法和误差补偿法[2]。误差防止法受到经济条件的约束，应用相对较少。误差补偿法通过计算机技术对产生的误差进行修正，成本较低。因此，许多研究人员对机床热误差补偿法进行了深入的研究。例如：文献[3-4]基于动态自适应加权最小二乘支持矢量机的方法构建机床热误差预测模型。采用动态的自适应方法，对建模选择的参数进行优化，根据热误差变量得到权重系数，最终确定最小二乘法支持矢量机机床的热误差预测模型。该方法建模精度较高，优于传统的最小二乘法。文献[5-7]基于神经模糊控制理论的建模方法创建机床热误差模型，将模糊神经网络建模方法与径向基函数神经网络建模方法进行了对比。对比结果显示，模糊神经网络建模方法精度更高，预测性能较好。文献[8-9]研究了数控机床热误差补偿分布滞后模型，通过模糊聚类法选择出测量机床温度的实验数据，从而拟合成分布滞后预测模型，并且与多元线性回归模型进行比较。结果显示，在同等条件下，分布滞后模型预测精度较高。以往研究的机床热误差预测模型预测精度虽然提高，但是比较繁琐，需要测量的温度数据较多。对此，本文采用自适应神经模糊推理系统的模糊C均值聚类法，对机床运动的温度数据进行筛选，选择出最优的温度数据。引入灰色理论系统创建热误差预测数学模型，通过实验数据对本文创建的热误差模型进行验证，并与其它预测模型进行对比。结果表明，本文所创建的机床热误差预测模型不仅需要的温度数椐较少，而且热误差补偿后误差明显减小，加工精度较高。

1 自适应神经模糊推理系统

1.1 ANFIS结构

ANFIS结构如图1所示，系统模型有五个层面，每个层面均包括了由节点函数定义的诸多节点。方框表示自适应可调参数的节点集，圆圈表示模型中固定参数的节点集。在ANFIS简化模型中，定义了两个输入变量(T1和T2)以及一个输出变量F(热漂移)。

在第一层面中：输入变量通过隶属度函数(MF)转化为一个模糊集，其中自适应节点的节点函数[10]为：

(1)

(2)

式中：T1和T2表示输入节点；i、A和B表示关节点的标注符号；μ(T1)和μ(T2)表示隶属度函数(MF)。文章选用最大为1和最小值为0的高斯型函数作为隶属度函数(MF)。在该层中参数为设定的自变量。

第二层面：该层中所有的节点均为固定节点，用圆圈标注。用M表示通过与输入变量相关的节点函数相乘得到相应的输出变量，如下所示：

(3)

式中：O2,i表示系统第二层面的输出量，输出信号wi反映了系统第二层的启动强度。

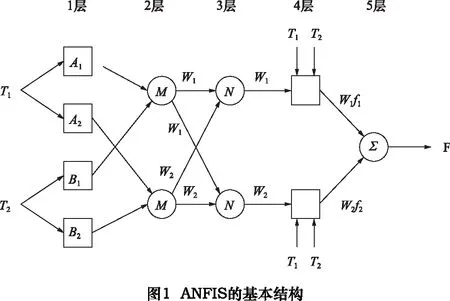
第三层面：该层中所有的节点均为固定节点，用圆圈标注。用N表示使启动强度标准化的过程，该过程是通过节点函数计算第i个节点的启动强度与所有节点启动强度的比值实现的。

(4)

式中：O3,i表示第三层面的输出量，数值w表示标准化后的启动强度。

第四层面：该层中所有节点均为自适应节点，用方框标注，其节点函数如下所示：

(5)

式中：f1和f2表示以下两种if-then模糊理论：

理论1：若T1是A1，T2是B1，则f1=p1T1+q1T2+r1。

理论2：若T1是A2，T2是B2，则f2=p2T1+q2T2+r2。

式中：pi、qi和ri表示参数集，称为因变参数。

第五层面：在该层中所有节点均为固定节点，用圆圈标注。用∑表示节点函数计算总的输出量：

(6)

1.2 模糊C均值(FCM)聚类法

模糊C均值聚类法是一种柔性聚类法，其通过隶属度确定每项数据的等级，并依此将各数据归类到相应数据集中。FCM算法作为K-均值聚类算法的模糊模型，其对各数据集之间的边界条件无严苛要求。因此，FCM算法的这一独特优点允许数据隶属于数据全集中不同的数据集，而不是仅只隶属于单一的数据集。

FCM将n个向量集xi，i= 1,2,…,n划分成模糊群组，并通过定义相应的聚类中心，从而可以减少相异性测量目标函数的计算量。k=1,2,…,c是从n个节点中任意选取的c个节点。因此，FCM算法可简要理解为：首先从n个任意数据集{x1,x2,x3,…,xn}中选取c个值作为系统c个聚类中心。其次，隶属度矩阵(μ)可通过如下的公式[11]计算：

(7)

式中：μkj表示聚类集k中的目标数据j的隶属度等级；m表示模糊指数，选取范围为[1,∞]；dij=‖ni-xj‖表示点ni与xj之间的欧几里德距离，dkj=‖ck-xj‖表示点ck与xj之间的欧几里德距离。

目标函数[11]值的计算公式如下所示：

(8)

i=1,2…，nj；j=1，2，…，n；k=1，2，…，c

模糊C均值聚类法的各个聚类中心值ck计算公式[11]如下所示：

(9)

利用FCM算法，根据隶属度函数将所有实验数据组划分成几个含有不同聚类中心的数据子集，每个子集都会相应的通过ANFIS进行演算。另外，通过FCM算法可以求得热误差补偿模型的最优温度数据集。

2 热误差数学模型

过多数量的热传感器会对热推算模型的稳定性及精确性造成不良影响，而制约热推算模型精确性的关键因素，同时也是建立热误差模型的难点在于热传感器安放位置的合理选择。

灰色系统理论是利用数学方法，基于较少的数据集和乏信息研究灰色系统的一种方法，该技术常用于针对部分信息已知、部分未知的系统。同时利用灰色系统理论，可以为热误差模型的建立确定传感器的合理安放位置。其最大的优点在于灰色系统理论可以在较少的实验数据及较少的数据分布下实现精确推算[12]。在众多灰色模型中，本文采用的是GM (1,N)模型。

一阶灰色模型GM (1,N)是针对多元素预测系统的多元灰色模型。GM (1,N)的含义是模型有N个变量，其中包括一个因变量以及N-1个自变量。假定模型有N个变量，(i=1,2,…,N)，每个变量有如下n个初始序列[13]：

(10)

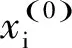
(11)

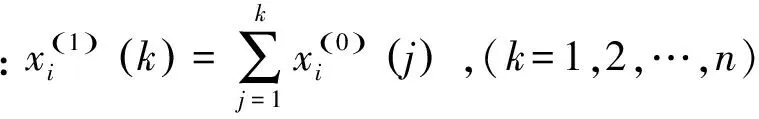
因此，GM(1,N)模型可用下列灰色微分方程表示[13]：

(12)

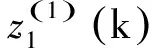
(13)

式中：系数a和bj分别表示系统开发参数和驱动参数。

模型系数通过最小二乘估算法[13]得出为：

(14)

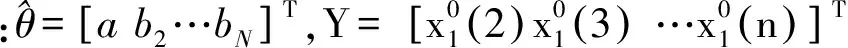
由灰色理论[13]得出，GM(1,N)时间响应近似方程式为

(15)

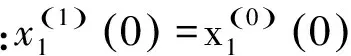
根据式(14)、(15)可以得出GM(1,N)模型热误差近似表达式为

(16)

3 实验验证与讨论

三轴立式铣床的方框图如图2所示，滚珠螺杠端部由轴承支撑并直接与驱动电动机轴相耦合。主轴由安置在主轴支架上的直流电机带动旋转，并控制其转速在1 000～2 000 r/min之间。安装在机床上的76个热传感器用来获取机床的温度参数，并按照表1中位置的不同进行了相应分类。

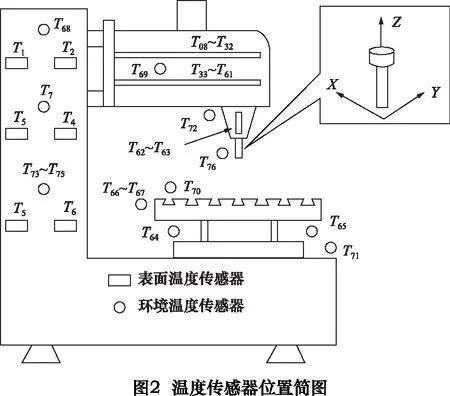
利用FCM算法所有热传感器影响权重值都会聚类成不同的组，以保证模型的稳定性。依据传感器热漂移的影响系数，从每个聚类组中选取一个温度传感器代表该组同温度类别的传感器，最后选择T18、T55、T63、T68和T71五个温度传感器，通过GM(1，N)模型预测热误差，然后进行补偿，如图3所示。

表1 温度传感器位置

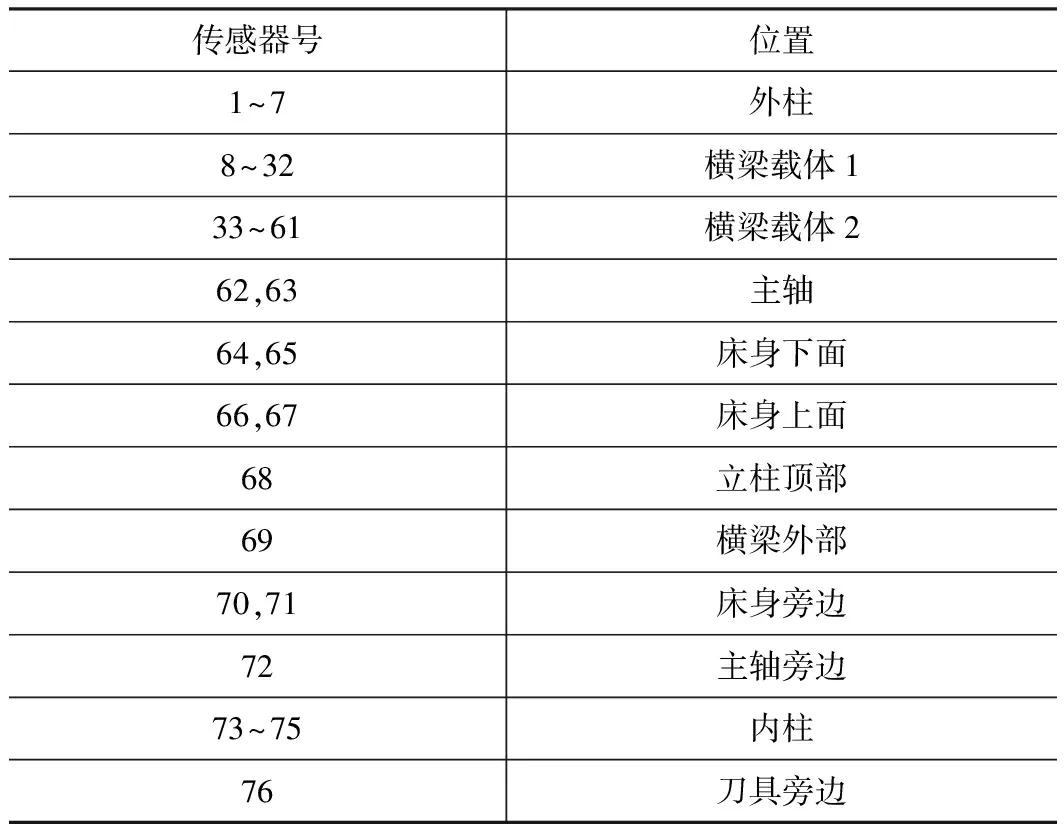
传感器号位置1～7外柱8～32横梁载体133～61横梁载体262，63主轴64，65床身下面66，67床身上面68立柱顶部69横梁外部70，71床身旁边72主轴旁边73～75内柱76刀具旁边

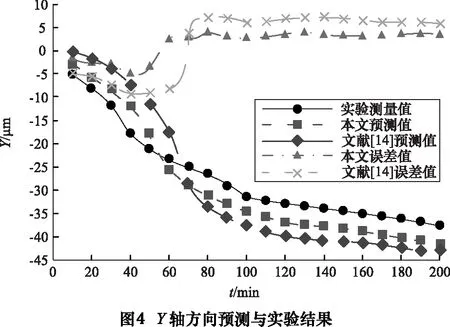
在本实验中，铣床转速设置为1 000 r/min运行80 min，接着转速改为2 000 r/min运行120 min，每隔10 min采集一次数据。由于在X轴方向热位移变形比较小，所以只对Y轴和Z轴方向位移变形量通过位移传感器进行采集，Y轴和Z轴方向的热误差通过补偿后的结果如图4、图5所示。

由图4、图5可知，补偿前，Y轴方向产生的最大误差为41.5 μm，Z轴方向产生的最大误差为33.8 μm。补偿后，文献[14]预测模型在Y轴方向产生的最大误差为9.2 μm，在Z轴方向产生的最大误差为8.6 μm，补偿后的误差都在10 μm以内。而本文预测模型在Y轴方向产生的最大误差为4.8 μm，在Z轴方向产生的最大误差为4.6 μm，补偿后的误差都在10 μm以内，热误差经过补偿后精度明显提高。

4 结语

本文采用了自适应模糊推理系统和灰色理论研究了数控机床热误差的预测模型。分析了自适应模糊推理系统的结构和模糊C均值聚类法，根据灰色理论创建热误差预测模型。通过模糊C均值聚类法筛选温度实验数据，确定出最佳温度测量数据，温度传感器从76个减少到5个。通过实验验证本文预测模型，并且与其它预测模型方法进行对比。预测结果表明，本文预测热误差经过补偿后所产生的最大误差在5 μm以内，其他方法预测热误差经过补偿后所产生的最大误差在10 μm以内。自适应模糊推理系统的模糊C均值聚类法耦合灰色理论创建的数控机床热误差预测模型预测精度较高，为机床运行的热误差补偿提供了参考依据。

[1]马晓波,仇健.立式数控机床主轴热态精度检测[J].工具技术,2013,47(7):60-63.

[2]陈海东.基于LabVIEW的数控机床热误差自动测量系统的设计[D].合肥:合肥工业大学,2014.

[3]林伟青,傅建中,陈子辰,等.数控机床热误差的动态自适应加权最小二乘支持矢量机建模方法[J].机械工程学报,2009,45(3):179-182.

[4]Xie C,Roddeck W,Liu C S,et al.The analysis and research about temperature and thermal error measurement technology of CNC machine tool[J].Key Engineering Materials,2012,392(10):40-44.

[5]余治民,刘子建,艾彦迪,等.基于神经模糊控制理论的数控机床热误差建模[J].中国机械工程,2014,25(16):2225- 2230.

[6]张宏韬,姜辉,杨建国.模糊神经网络理论在数控机床热误差补偿建模中的应用[J].上海交通大学学报,2009, 43(12):1950-1952.

[7]Tseng Pai-Chung, Chen Shen-Len.The neural fuzzy thermal error compensation controller on CNC machining center[J].JSME International Journal,2012, 45(2):471-477.

[8]苗恩铭,龚亚运,徐抵尚,等.数控机床热误差补偿模型稳健性比较分析[J].机械工程学报, 2015,51(7):130-134.

[9]姚焕新,牛鹏程,龚亚运,等.数控机床热误差补偿中分布滞后模型的建立[J].农业机械学报,2013, 44(3):246-249.

[10]Lee Jin-Hyeon, Lee Jae-Ha, Yang Seung-Han. Thermal error modeling of a horizontal machining center using fuzzy logic strategy[J].Journal of Manufacturing Processes,2011,3(2):120-126.

[11]王纵虎,刘志镜,陈东辉.基于粒子群优化的模糊C-均值聚类算法研究[J].计算机科学,2012,39(9):166-169.

[12]Abderrazak El Ouafi,Michel Guillot.A comprehensive approach for thermal error model optimization for ANN -based real-time error compensation in CNC machine tools[J].Mechanical and Aerospace Engineering ICMAE, 2012,232(9):640-646.

[13]张伟.基于灰色系统理论的数控机床热误差建模技术研究[D].南京:南京航空航天大学,2013.

[14]Lee Jin-Hyeon, Yang Seung-Han.Statistical optimization and assessment of a thermal error model for CNC machine tools [J].International Journal of Machine Tools & Manufacture,2012,42(2):148-154.

(编辑 汪 艺)

如果您想发表对本文的看法，请将文章编号填入读者意见调查表中的相应位置。

Research on thermal error compensation of machine tool based on adaptive neuro fuzzy inference system and grey theory

DING Qunyan①, ZENG Xin②

(①School of Electronic Engineering, Wuhan Polytechnic College of Software and Engineering, Wuhan 430205, CHN; ②School of Automotive Engineering, Wuhan Polytechnic College of Software and Engineering, Wuhan 430205, CHN)

An adaptive neural fuzzy inference system (ANFIS) model is proposed, which is based on the grey theory to model the thermal error, and to minimize the value of the positioning error of machine tool machining parts. Using the adaptive fuzzy inference system of fuzzyC-means clustering algorithm, the temperature sensor of machine tool for grouping and clustering analysis, select each optimal temperature sensor, measurement temperature sensor will be reduced from 76 to 5. Grey system theory is put forward, and the formula of GM (1,N) is deduced, and the thermal error prediction model is established. The error generated by the machine tool is verified by the experimental measurement method. The experimental results show that the maximum value of thermal error ofYaxis andZaxis is 41.5 μm and 33.8 μm, respectively, and the maximum value of thermal error ofYaxis andZaxis is 4.8 μm and 4.6 μm respectively. Using adaptive neuro fuzzy inference and grey system to compensate the thermal error of machine tool, measure not only reduce the number of temperature sensor and generated by the operation of the machine tool spindle error is significantly reduced, high precision machining, the effect is very good.

numerical control machine tool; adaptive fuzzy inference system; fuzzyCmean clustering method; grey theory; thermal error compensation

*湖北省自然科学基金资助项目(2013CD10903)

TH161

A

10.19287/j.cnki.1005-2402.2016.12.011

2016-08-17)

161219