基于仿真大数据的效能评估指标体系构建方法

司光亚，高翔，刘洋，吴琳

国防大学信息作战与指挥训练教研部，北京 100091

基于仿真大数据的效能评估指标体系构建方法

司光亚，高翔，刘洋，吴琳

国防大学信息作战与指挥训练教研部，北京 100091

针对武器装备效能评估指标体系中评估指标之间存在的相互依赖与影响的关系以及评估过程主观性较强的情况，提出一种基于仿真大数据采用超网特征参数和ANP相结合构建指标体系的方法。以某次武器装备体系仿真为例，给出了网络化评估指标体系构建流程，并建立了具体的指标体系，同时对指标之间的关联性进行了深度挖掘。实验结果表明，提出的指标体系构建方法具有合理性和有效性，能够为武器装备体系效能评估提供更为可靠的理论依据。

仿真大数据；效能评估；ANP；关联性分析；网络化指标体系

1 引言

现代武器装备体系是典型的复杂系统，呈现出网络化特点。它的整体性、非线性、涌现性以及不确定性等复杂特征使得长期以来在武器装备体系效能评估方面的研究进展缓慢，严重影响了武器装备体系的建设与发展。指标体系建设是进行效能评估的基础和依据。由于武器装备体系效能评估需要更多地反映体系效能评估的特点，传统的“树状”武器装备评估指标体系和“加权求和”方法已不再适用[1,2]。如何对武器装备体系的网络化特点及其“涌现效应”进行研究，并深度挖掘各指标之间的关联关系，构建全新的相互关联的网络化指标体系，是需要解决的一项关键问题。因此，必须寻找新的方法构造全新的效能评估指标体系框架，在此基础上，构建具体的指标体系，展开对武器装备体系效能的有效评估。

许相莉等人[3]提出了一种基于复杂网络理论的网络化指标体系框架，并以实际对抗推演中的指控体系为例构建了具体的指标体系，但是没有给出构建指标体系的具体方法，同时传统的复杂网络模型已经不适于描述体系。刘旸等人[4]提出信度层次分析法，按照权威领域专家在不同置信区间内的置信度，对某型导弹驱逐舰的作战效能进行了评估，但是该方法缺乏考虑评估指标之间的相互影响与依赖关系。赵刚等人[5]依据风险评估规范选取信息安全风险评估指标，运用网络层次分析法（analytic network process, ANP）求出各评估指标的影响权重，从而对信息系统的安全风险进行综合评价，但是该方法的评估数据主要来源于专家的经验判断，具有较强的主观性。石福丽等人[6]提出了基于网络层次分析法和仿真的武器装备能力幂指数评估模型构建框架，研究了网络化评估指标体系设计与优化方法，但是该方法不适于对体系整体进行效能评估。

针对上述问题，本文依托现有的大型仿真系统，引入与体系具有天然结构类似性的超网络模型，利用推演过程中产生的海量多源异构仿真大数据，构建武器装备体系加权超网模型。在此基础上，基于ANP构建网络化的效能评估指标体系，同时利用数据挖掘技术分析效能指标体系中指标之间的关联性，从而实现对武器装备体系的效能评估。

通过大型仿真推演与实验得到的仿真大数据，涵盖了陆、海、空、天多维战场空间的全过程推演产生的全样本时空数据，仿真实体规模庞大，为挖掘武器装备体系结构提供了可能；记录了仿真推演中种类繁多、数量庞大的实体及其之间的复杂交互关系的数据，为效能评估指标体系的相关性分析提供了可能；完整记录了仿真推演的过程与结果数据，为展现难以可视化的不确定性和涌现性效能提供了可能。为此，仿真大数据为武器装备体系效能评估提供了新的思路。

笔者主要基于具有关联性特征的仿真大数据，跳过因果关系，通过动态测量的方法对各指标之间的关联关系进行深度挖掘。以武器装备体系仿真产生的数据为分析对象，若指标参数之间是线性关系，利用最小二乘法（多元线性回归）通过对各项效能指标的演化进行动态测量，充分挖掘各个层次指标之间的网状关联性；若指标参数之间是非线性关系，此时拟采用深度神经网络（deep neural network，DNN）来分析其关联性。

2 效能评估指标体系构建

指标体系，是指在评估活动中由一系列相互关联的本质属性指标构成的有机整体。构建评估指标体系是进行武器装备体系效能评估的首要前提。首先利用ANP构建效能评估指标体系，在此基础上以仿真大数据为分析对象，结合回归方法和深度学习方法挖掘指标之间的关联性。

2.1 指标体系构建方法的概念框架

图1给出了指标体系构建方法的概念框架，该框架主要由加权超网模型构建与指标体系构建两个核心模块组成。

（1）加权超网模型构建模块

首先对获取的仿真大数据进行预处理，这里的仿真大数据包括日志数据、报告数据、指令数据等。经过必要的清洗、转换和集成后，根据参考文献[7]中加权超网模型的构建算法构建模型。

（2）指标体系构建模块

在构建加权超网模型后，与管理人员的评估目标进行交互，通过动态测量不同的超网特征参数来构建指标体系中的基础评估指标，并基于 ANP构建效能评估指标体系。

2.2 网络层次分析法

本文拟运用网络层次分析法（ANP）[8,9]设计和构建评估武器装备体系效能的多层次、多类别、相互关联的网络化指标体系。

ANP模型的基本步骤如下。

· 分析问题，将决策问题进行系统的分析、组合，形成元素和元素集，主要分析判断元素层次是否内部独立，是否存在内部依存和反馈。

· 构造ANP的典型结构，首先要构造控制层，设定决策目标和决策准则。控制层中若有两个以上准则，则这些准则对上隶属于目标，对下分别控制着一个网络结构。再则构造网络层次，分析其网络结构和相互影响关系。

· 构造 ANP的超矩阵计算权重，对组内和组与组之间的相关元素逐个进行两两比较，即计算超矩阵，计算相对权重。

典型的网络化评估指标体系如图2所示。该体系由若干个指标簇构成，彼此互不隶属，互不独立。每个指标或指标簇彼此都不独立，某一个指标簇可能影响整个网络化评估指标体系中的任一指标簇，反之亦可能受其影响。指标簇中的指标之间可能相互影响，也可能影响另一指标簇或受其影响。

图1 指标体系构建方法的概念框架

2.3 评估指标的选取

根据Cares J[10]的《分布式网络化作战—网络中心战基础》一书中对分布式网络化部队基本作战能力指标的描述，拟确定效能度量指标为：抗毁性R1、重组性R2、分散性R3、隐蔽性R4、邻近性R5、灵活性R6、适应性R7和高效性R8。

武器装备体系是由超大规模的传感器、指挥控制、通信等实体或系统由各种有线或无线方式连接而成的复杂系统。由于超网模型与体系具有天然的结构类似性，因而利用超网对武器装备体系进行建模与评估已成为该领域的研究热点。本文根据参考文献[7]的相关研究成果，在构建武器装备体系加权超网模型后，通过模型的特征参数（如节点数量、度、层级、连通度等）构建指标体系中的基础评估指标。拟确定的基础评估指标包括节点数量A1、度A2、层级A3、网络重心数量及分布A4、连通度A5、链路节点比A6、介数A7、中立率A8、集群数量和集群规模A9。

在此基础上，通过测量各指标的动态演化过程，充分挖掘各指标之间的网络化关联关系，构建基础评估指标与效能度量指标之间的关联关系，并通过海量仿真数据对各指标展开基于动态测量的相关性分析，挖掘它们之间的关联性，形成具体、完整的相互关联的网络化效能指标体系。

下面分别对上述效能度量指标和基础评估指标进行介绍[3]。

效能度量指标主要度量和表现武器装备体系的建设成果，如对体系的自适应能力、重组能力、抗毁性、分散性、隐蔽能力、灵活性、高效性等能力的评估。系统效能度量指标如下。

· 抗毁性R1：体系结构被破坏的难易程度，即网络在遭受破坏时保持一定连通状态的性能。

· 重组性R2：迅速重新部署或集结各要素的能力，自适应地演变成一定数量的节点、连接拓扑以及产生有价值的自适应行为的多尺度性能。

· 分散性R3：空间、信息、逻辑的分散程度，避免具有中心结构。

· 隐蔽性R4：节点的隐蔽能力，通过较小的单元组合来提高凝聚能力，降低被发现的概率。

· 邻近性R5：网络结构在信息和逻辑上的完备能力，突出大量较小的隐蔽目标在信息上和逻辑上对作战能力的贡献。

· 灵活性R6：互操作能力，适应激烈竞争和环境剧变，这是从重组性独立出来的。

· 适应性R7：网络的自适应能力。

· 高效性R8：体系的效率、瓶颈情况等。

基础评估指标反映的是武器装备体系的整体性能，拟通过加权超网模型的特征参数进行基础评估指标的构建，这些指标又可以分为个体行为评价指标和体系整体行为评价指标，如图3所示。

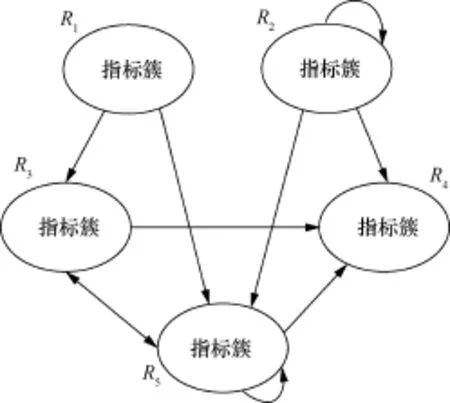
图2 网络化评估指标体系

其中，个体行为评价指标主要的评价对象是武器装备体系中个体及其交互行为构成的结构和行为特性，拟确定的指标包括：活动节点数量、度、层级、功能重心数量及分布和介数。体系整体行为评价指标主要的评价对象是体系整体行为特性以及整体结构特性，拟确定的指标包括：连通度、链路节点比、中立率以及集群数量和集群规模。下面分别对这些指标进行介绍。

· 活动节点数量A1：武器装备体系中处于活动状态的节点数量。具体地，是指各个功能网络中处于活动状态的节点数量。

· 度A2：包括体系中节点的入度、出度、平均度、最大度、度分布指标。其中，度分布p(k)定义为任选一个节点，它的度正好为k的概率。

· 层级A3：武器装备体系节点之间关系的平均层级数、最大层级数。指挥层级指的是指挥信息流从一个作战实体到另一个作战实体必须流经的实体数。指挥层级可以用复杂网络的平均路径长度来表示。

· 功能重心数量及分布A4：武器装备体系的功能重心情况。对于静态网络，最大网络中心节点就是网络中总度数最大的节点，该节点在整个网络中十分重要，根据网络的拓扑结构，可以认为它（们）是网络重心。

· 连通度A5：武器装备体系的连通度，指武器装备体系的各组成系统向体系内部的其他系统寻求、获取、提供信息和服务的能力。评价复杂网络连通度可以选定谱范数。

· 链路节点比A6：武器装备体系的链路节点比，可用于衡量体系的脆弱性和自适应性等，它指的是网络中的链路总数和网络节点总数的比值。

· 介数A7：衡量武器装备体系的瓶颈情况，包括体系的介数中心数量、最大节点介数、介数分布情况等指标。

· 中立率A8：武器装备体系的中立率，主要用于衡量体系的自适应性。对于一个节点数为N的网络，用链路的数量L减去网络的大小N-1，然后再用网络规模N进行归一化。

· 集群数量和集群规模A9：武器装备体系结构中的连通片数量、每个连通片内的节点数量、每个集群的重心情况。

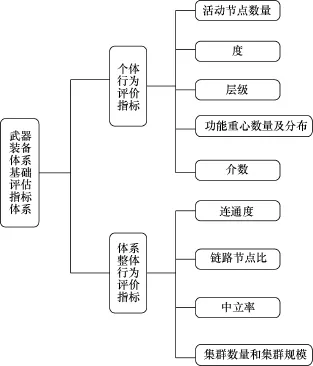
图3 武器装备体系基础评估指标

除了上述指标，还有其他描述体系网络的特征参量，例如连通子图、聚类系数、网络结构熵、特征谱等。选取何种特征参量作为体系的网络化效能评估指标，取决于体系网络模型的实际含义。

2.4 评估指标体系的简化方法

目前，评估模型的复杂、收集数据的繁多已给评估组织者、数据提供者、评估专家带来很大的负担，评估模型简化显然有其现实的意义，主要体现在以下几点：简化的评估模型使得数据处理更加容易；简化的评估模型会大大节约时间；简化的评估模型使得对评估过程的控制更加容易；简化的评估模型会提高评估实施的可行性。

指标体系简化主要有两种方式，一是指标变量个数的减少；二是组合方式的简化。组合方式简化还包括这样一种情况，即指标本身并不改变，但指标变量的性质发生了变化，从而使得评估简单易行。

为此，以仿真大数据为基础并结合高维数据降维思想，对指标体系中的指标进行简化。在初步构建网络化效能评估指标体系后，本文采用了主成分分析法对指标体系进行化简。

2.5 网络化效能评估指标体系构建

本文以某次体系仿真推演产生的海量数据为研究对象，构造武器装备体系加权超网模型，同时利用超网模型的特征参数进行基础评估指标的构建，并对效能度量指标进行确定。在此基础上，基于ANP模型建立效能评估指标体系。图4给出了效能评估指标体系的构建流程，具体如下。

· 目标分析是建立评估指标体系的前提，就是体系评估要达到的目的，即武器装备体系评估结果最重要的不是“好坏”，而是“发现”，发现体系结构、能力和效能上的问题，提高对体系的认知。

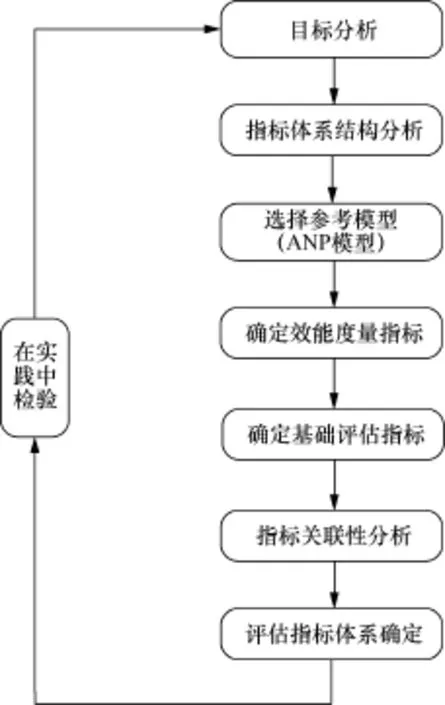
图4 指标体系构建流程

· 指标体系结构分析。不同的目标结构会带来不同的评估指标体系结构形式，常见的评估指标体系的结构形式有两种：层次型评估指标体系和网络型评估指标体系。由于现代武器装备体系是典型的复杂系统，呈现出网络化特点，故拟建立网络状的评估指标体系。

· 选择参考模型。按复杂系统理论的观点，武器装备体系作战效能“整体性质不等于部分之和”，而是组成体系的众多分系统完成特定作战任务过程中涌现出来的体系作战能力，故利用ANP模型设计和构建评估武器装备体系效能的网络化指标体系。

· 一般而言，体系级的效能指标需要反映体系整体效果。根据武器装备体系效能评估的需要，确定的效能度量指标分别为抗毁性R1、重组性R2、分散性R3、隐蔽性 R4、邻近性R5、灵活性R6、适应性R7以及高效性R8。

· 基础评估指标是作战仿真实验结果观察到的、对战场形势具有决定作用的敌我双方战况数据的集合。确定的基础评估指标分别为活动节点数量A1、度A2、层级A3、功能重心数量及分布A4、连通度A5、链路节点比A6、介数A7、中立率A8以及集群数量和集群规模A9。

· 指标关联性分析。通过指标关联性分析，可以得到各个指标在综合评估中的地位和影响程度。

· 在上述各项工作完成后，便可以形成一个初步的、可供实际操作的评估指标体系。此外，还需要在实践中检验，并基于评估结果提出改进建议，以得到满意的综合评估指标体系。

图5给出了初步构建的网络化效能评估指标体系。该指标体系的结构包括：基础评估指标Ai、效能度量指标Ri、指标之间的关联关系。

在该指标体系中，基础指标与能力效果之间存在聚合关系。以抗毁性R6能力效果的评估为例，它与A4和A5、A6、A74类单项基础指标存在聚合关系，这4类指标项的单项度量结果将影响抗毁性能力效果。同时，指标之间存在影响关系，例如邻近性R5和灵活性R6相互影响，此时使用双箭头连接线进行表示。而当效能指标R中的内部节点也存在关联关系时，使用单箭头曲线指向自己，如邻近性R5。

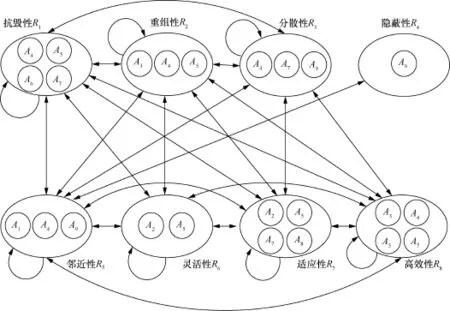
图5 网络化效能评估指标体系

3 基于深度学习和ANP相结合的指标关联性挖掘方法研究

传统的树状指标体系难以反映武器装备体系的复杂系统特征和作战效能生成机理，笔者主要基于具有关联性特征的仿真数据，跳过因果关系，通过动态测量的方法，对各指标之间的关联关系进行深度挖掘。以武器装备体系仿真产生的数据为分析对象，若指标参数之间是线性关系，利用回归分析中的最小二乘法通过对各项效能指标的演化进行动态测量，充分挖掘各个层次指标之间的网状关联性；若指标参数之间是非线性关系，此时拟采用深度神经网络（DNN）来分析其关联性。

图6给出了评估指标体系关联性挖掘的流程。

首先，分析效能度量指标之间的权重关系，根据专家给出的经验数据，拟采用德尔菲（Delphi）法计算效能度量指标之间的权重，建立加权矩阵。基本过程如下。

设指标体系草案选定有n个评估指标I1,I2,…,In，经过专家意见咨询并统计结果，综合专家意见的总重要度分别为x1,x2,…,xn，对指标总重要度排序进行归一化处理，得到n个评估指标的归一化排序向量(w1,w2,…,wn)，且w1+w2+…+wn=1。

其次，动态测量基础评估指标的仿真参数，即通过仿真分析某些定量指标之间的关联度，获取构建初始超矩阵所需的参数。若指标参数之间属于线性关系，可以采用最小二乘法。基于最小二乘法的基本过程：假设输入的一组基础评估指标为A=(a1,a2,…,am)，其中，ai为第i个指标。这组指标影响上层效能度量中的指标为y，Aj(j=1,2,…,n)为第j时刻的实验指标值。使用最小二乘法建立各指标值与效能度量指标之间的拟合关系回归模型，进而针对n个基础评估指标求得其对y的影响系数向量B=[b1,b2,…,bn]T，将这些影响系数进行两两比较，可以形成由相对重要度构成的判断矩阵为C=(bi/bj)n×n=(cij)n×n。在此之后，对该判断矩阵进行微调，使其符合指标判断要求。若指标参数之间属于非线性关系，此时拟采用DNN分析各个指标的关联性。图7给出了一个含多个隐层的深度神经网络模型，该模型的输入维度是5，若设其层数为δ，则神经元的个数为(δ-1)×5+1。

当今深度学习（deep learning）正处于快速发展阶段。其基本思想就是通过组合低层特征形成更加抽象的高层表示特征，即第i层的输出作为第i+1层的输入。DNN在计算机视觉领域的表现可谓见效非凡，如DNN在Google（谷歌）的Brain项目中的应用。

最后，按顺序构造出初始超矩阵和极限超矩阵，进而可以挖掘评估指标体系关联性。这里求解超矩阵是一种非常复杂的计算过程，手工运算几乎不可能。在实际应用中，一般都使用计算机软件进行计算，例如Super Decisions，并且采用的计算方法是Calculus type（9.0）。

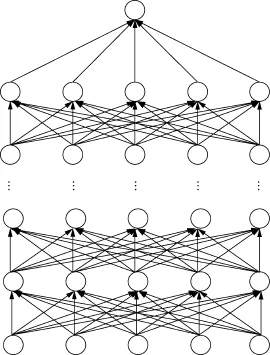
图7 含多个隐层的深度神经网络模型

4 应用实例

4.1 参数设置

以某次大型仿真对抗推演为例，对文中的模型与相关计算方法进行验证。该次仿真推演与实验涵盖了陆、海、空、天、电多维战场空间，仿真实体规模庞大，采集了整个推演的全过程、全样本时空数据，为挖掘武器装备体系结构以及对其进行效能评估提供了可能。

首先，根据参考文献[7]中的方法，通过采集仿真系统产生的数据构造加权超网模型。在此基础上，通过动态测量超网模型特征参数获取基础评估指标值。之后，根据Delphi法计算效能度量指标之间的权重，通过咨询相关专家的意见并统计结果，得到各个效能指标的权重，并建立加权矩阵。

在建立基础评估指标判断矩阵过程中，通过动态测量基础评估指标仿真参数，获取构建初始超矩阵需要的参数。例如，对于指标活动节点数量y，层级x1、功能重心数量x2、连通度x3对其有影响，本问题涉及的3个指标都属于基础评估指标，可通过构建武器装备体系超网模型进行获取，通过动态测量得到不同时刻的超网特征参数，如下所示。

根据上述介绍的最小二乘法，建立3个基础评估指标与活动节点数量指标值之间的回归模型以及符合9个标度要求的判断矩阵。同时，可以计算得到评估指标的初始权重。

回归方程式为：

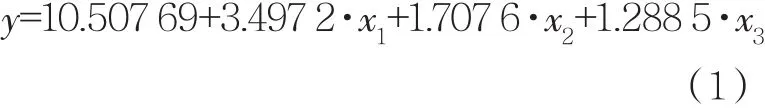
初始判断矩阵为：

符合9个标度要求的判断矩阵为：

通过计算得到以上3个基础评估指标的初始权重分别为：0.548 5、0.240 9、

0.210 6，代入初始超矩阵。

需要说明的是，若指标参数之间是非线性关系，此时采用DNN分析其关联性。

4.2 实验结果及分析

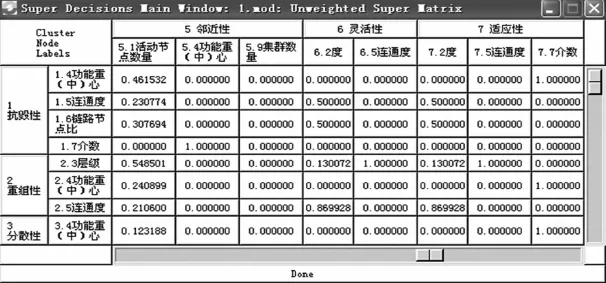
图8 初始超矩阵

类似地，计算全部指标对应的初始权重，得到初始超矩阵如图8所示。同时，得到的加权超矩阵如图9所示。

本文利用软件Super Decisions进行计算，得到评估指标的极限超矩阵如图10所示，从而获得各个评估指标最终权重。

如图10所示，以效能评估指标中的抗毁性R1为例，研究超网特征参数中的功能重心数量及分布A1、连通度A5、链路节点比A6和介数A74类单项基础指标对它的影响。指标A4、A5、A6和A7的计算权重分别为0.047 783、0.039 968、0.020 025和0.048 336，根据计算结果对A4、A5、A6和A7进行合成排序，得到4类单项基础指标的最终权重分别为0.306、0.256、0.128和0.31。

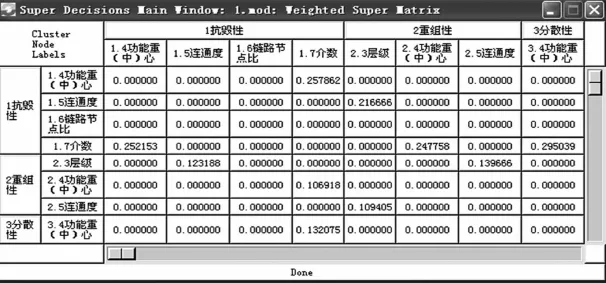
图9 加权超矩阵

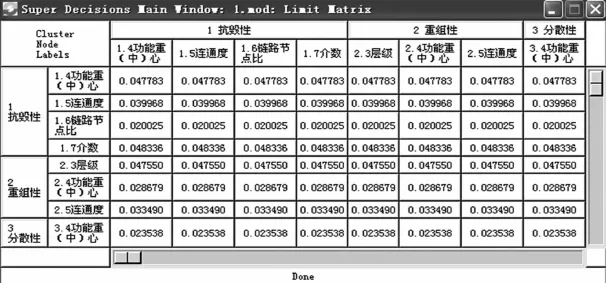
图10 极限超矩阵

由此可知，在上述指标中，重心数量及分布A4和介数A7二类单项基础指标对评价武器装备体系抗毁性所占的权重比较大，这与实际分析结果一致，从而验证了本文方法的合理性和可靠性。在此基础上，可以根据参考文献[6]中的幂指数评估模型计算得到体系的综合效能指数，从而实现对武器装备体系的效能进行评估。该方法是用相对数值简明地反映分析对象特性的一种量化方法。

5 结束语

本文提出了基于仿真大数据的采用超网特征参数和ANP相结合构建指标体系的方法，深入研究了建模过程，并给出了指标选取方法、指标体系的简化方法以及指标关联性挖掘方法。在此基础上，以某次武器装备体系仿真为研究对象，完成了具体指标体系的实例构建，并以实际仿真推演数据进行了实例性仿真评估，验证了评估方法的合理性和有效性。本文提出的指标体系构建方法为研究人员评估武器装备体系效能提供了有效的方法论指导与技术支持，可以直接服务于武器装备体系论证。

[1] 胡晓峰, 许相莉, 杨镜宇. 基于体系视角的赛博空间作战效能评估[J]. 军事运筹与系统工程, 2013, 27(1): 5-9. HU X F, XU X L, YANG J Y. Operational effectiveness evaluation of cyberspace based on the perspective of system [J]. Military Operations Research and Systems Engineering, 2013, 27(1): 5-9.

[2] 张杰, 唐宏, 苏凯, 等. 效能评估方法研究[M].北京: 国防工业出版社, 2009: 1-15．ZHANG J, TANG H, SU K, et al. Research on efficiency evaluation method[M]. Beijing: National Defense Industry Press, 2009: 1-15.

[3] 许相莉, 胡晓峰. 一种基于复杂网络理论的网络空间作战效能评估指标体系框架[J]. 军事运筹与系统工程, 2014, 28(1): 33-37, 41. XU X L, HU X F. A framework of evaluation index system of network space operational effectiveness based on complex network theory[J]. Military Operations Research and Systems Engineering, 2014, 28(1): 33-37, 41.

[4] 刘旸, 孟梅, 张恒, 等. 面向任务的驱逐舰作战效能评估方法研究[J]. 哈尔滨工程大学学报, 2013, 34(12): 1479-1489. LIU Y, MENG M, ZHANG H, et al. Research on the method of operational effectiveness evaluation oriented to the combat mission for destroyers[J]. Journal of Harbin Engineering University, 2013, 34(12): 1479-1489.

[5] 赵刚, 吴天水. 结合灰色网络威胁分析的信息安全风险评估[J]. 清华大学学报(自然科学版), 2013, 53(12): 1761-1767. ZHAO G, WU T S. Information security risk assessment based on G-ANP[J]. Journal of Tsinghua University(Science and Technology), 2013, 53(12): 1761 -1767.

[6] 石福利, 杨峰, 许永平, 等. 基于ANP和仿真的武器装备作战能力幂指数评估方法[J]. 系统工程理论与实践, 2011, 31(6): 1086-1094. SHI F L, YANG F, XU Y P, et al. Power index method for operational capability evaluation of weapon equipment based on ANP and simulation[J]. Systems Engineering-Theory&Practice, 2011, 31(6): 1086-1094.

[7] 高翔, 吴琳, 刘洋, 等. 基于加权超网模型的武器装备体系效能分析[J]. 指挥与控制学报, 2015, 1(2): 175-180. GAO X, WU L, LIU Y, et al. Weapon system-of-systems effectiveness analysis based on weighted network of networks model[J]. Acta Command and Control, 2015, 1(2): 175-180.

[8] 孙宏才, 田平, 王莲芬. ANP与决策科学[M].北京: 国防工业出版社, 2011: 45-57. SUN H C, TIAN P, WANG L F. Network analytic hierarchy process and decision science[M]. Beijing: National Defense Industry Press, 2011: 45-57.

[9] 樊蓓蓓, 祁国宁, 俞涛. 基于网络分析法的模块化产品平台中零部件模块通用性分析[J]. 计算机集成制造系统, 2013, 19(5): 918-925. FAN B B, QI G N, YU T. Network analysis method for commonality analysis of parts modules in modules in modular product platform[J]. Computer IntegratedManufacturing Systems, 2013, 19(5): 918-925.

[10] CARES J. Distributed networked operations: the foundations of network centric warfare[M]. Nebraska: iUniverse, 2005: 35-48.

Method for building effectiveness evaluation index system based on big simulation data

SI Guangya, GAO Xiang, LIU Yang, WU Lin
The Department of Information Operation & Command Training, NDU of PLA, Beijing 100091, China

In order to cope with the interdependence and interrelationship between evaluation criteria in effectiveness evaluation index system, and to eliminate the subjectivity of expert’s preference in the evaluation process, making use of big simulation data, a method of building index system based on big simulation data of supernetting characteristic parameter and ANP was proposed. Then, by taking a weapon SoS simulation scenario as example, a process of building networked evaluation index system was proposed and the corresponding networked index system was built. Simultaneously, the correlation between criteria was deeply mined. The example analysis verifies the reasonability and effectiveness of proposed method for building evaluation index system. It provides reliable theoretical basis for weapon SoS effectiveness evaluation.

big simulation data, effectiveness evaluation, analytic network process, correlation analysis, networked index system

TP391.9

A

10.11959/j.issn.2096-0271.2016042

司光亚（1967-），男，国防大学信息作战与指挥训练教研部教授、总工程师，主要研究方向为战争复杂系统建模仿真。

高翔（1984-），男，国防大学信息作战与指挥训练教研部博士后，主要研究方向为体系分析与超网建模。

刘洋（1975-），女，博士，国防大学信息作战与指挥训练教研部副教授，主要研究方向为计算机战争模拟。

吴琳（1974-），男，博士，国防大学信息作战与指挥训练教研部教授、博士生导师，主要研究方向为复杂系统与网络、战争复杂系统建模。

2016-06-20

军民共用重大研究计划联合基金资助项目（No.u1435218）；国家自然科学基金资助项目（No.61403401, No.61273189, No.61374179）

Foundation Items:The Union of National Natural Science Foundation and the General Equipment Department of China (No.u1435218), The National Natural Science Foundation of China (No.61403401, No.61273189, No.61374179)