基于嵌套模型的地下水侧向径流边界刻画方法研究
——以湖北碾盘山冲积平原地下水数值模拟为例
汪祯宸,陈植华,徐 栋,彭 康
(1.中国地质大学(武汉)环境学院,湖北武汉430074;2.中国海洋大学环境科学与工程学院,山东青岛266100)
基于嵌套模型的地下水侧向径流边界刻画方法研究
——以湖北碾盘山冲积平原地下水数值模拟为例
汪祯宸1,陈植华1,徐 栋2,彭 康1
(1.中国地质大学(武汉)环境学院,湖北武汉430074;2.中国海洋大学环境科学与工程学院,山东青岛266100)
侧向径流边界的刻画方法是地下水数值模拟中的关键问题。以湖北碾盘山汉江水利水电枢纽工程为例,基于有限单元法和嵌套模型的水量转换方法,分别建立包括完整水文地质单元的区域模型和仅包含汉水Ⅰ级阶地的平原区模型;通过区域模型的分区水均衡运算,计算平原区侧向径流边界的径流量,并以区域模型水均衡为框架,分别采用二类流量边界和一类水头边界刻画侧向径流边界,建立了平原区模型;深入分析区域模型和平原区模型间参数和水量的转换关系,并对比了两类边界条件刻画方法的优缺点和适用条件。结果表明:采用嵌套模型能够得到较为准确的地下水侧向径流量;在平原区模型中采用二类流量边界刻画侧向径流边界有利于提高平原区模型的精度和稳定性;边界条件除具有双重含义外还具有双重特征,在模型建立过程中应充分认识边界条件的位置特征和数量特征,并合理概化。
地下水;侧向径流边界;数值模拟;嵌套模型;水均衡
地下水数值模拟技术是定量研究平原区地下水的重要手段,因控制的钻孔数据限制,模拟范围往往圈定一个较小范围而非一个完整的水文地质单元,涉及一条或多条非天然边界。非天然边界的数值特征具有不确定性,不合理的处理将导致模拟结果产生严重失真,因此非天然边界的刻画方法具有重要的研究价值。本文以湖北碾盘山水利水电枢纽工程关山堤至朱堡堤一线为例,研究汉江冲积平原地下水侧向径流边界的刻画问题。
1 侧向径流边界的特征及其刻画方法
地下水数值模拟的边界条件具有双重含义[1]:其一作为地下水数值模型的定解条件,以描述系统边界的特定状态;其二确定了目标系统与周围环境之间的相互作用关系,即系统间的物质、能量交换。天然条件下,一个完整水文地质单元的边界相对易于刻画,属于数值特征明确的确定性边界。例如区域分水岭地下水通量为零,可以概化为零通量边界;大型地表水体水位动态易于测量,水量充沛,在与地下水水力联系紧密的条件下可以概化为水头边界。
侧向径流边界是相邻地下水系统间的一种联系方式,系统间通过侧向径流发生水量交换。侧向径流边界的数值特征受气候、地质条件、人为扰动等多重影响,其位置和形态的选取具有一定随意性,且不易观测,属于不确定性边界。侧向径流边界常被刻画为一类水头边界或二类流量边界,其刻画过程主要包括:①边界位置的地下水位动态观测,观测孔应分布于边界沿线及两侧,观测时长应包括一个完整水文年;②边界水位统计和流量计算,通过动态数据分析,选择某条变幅极小的等水位线设为一类水头边界,或通过边界两侧水位差计算边界处水力梯度和单宽流量,设定二类流量边界;③观测资料少的情况下可以采用迭代逼近的方法或者滚动预测方法[2]反演边界水位或流量。
关山堤至朱堡堤一线汉江冲积平原是碾盘山水利水电枢纽工程的重要影响范围,区内地质结构、岩土性质简单,地下水监测资料丰富,以冲积平原区为模型范围有利于得到较高的模拟精度和较好的收敛性和稳定性。然而冲积平原区并非完整的地下水系统,该区接受西侧地下水侧向径流补给,侧向径流边界的刻画方式和合理性将对冲积平原区地下水模型流场产生至关重要的影响。因此,在建立平原区地下水数值模型过程中,应优先确定侧向径流边界的刻画方法。
但上述刻画侧向径流边界的方法不适用于本次研究,分析原因主要在于:一是尺度效应造成的规模误差,这种尺度效应产生的误差主要体现在大尺度过程常常仅能获得点样本或小尺度观测值,但受到模拟技术水平的约束,模拟尺度总比观测尺度来的大或者小[3],而研究区分布不均、数量有限的点状勘察及监测资料,对于侧向径流边界属于小尺度观测值,具有一定程度的特殊性,达不到侧向径流边界的刻画精度;二是研究区内将修建碾盘山水力水电枢纽工程,水库蓄水将导致地下水位抬升,而水位变幅受多种因素影响[4-5],将天然地下水位概化为定水头边界将会增大模拟误差;此外,迭代逼近方法或者滚动预测方法仅考虑了目标模型内的监测数据,忽略了模型区域外的流场状态,也可能存在误差。
为了解决上述问题,本文采用嵌套模型的水量转换方法[6-7]研究侧向径流边界的刻画方法,并研究其精度及合理性。主要研究步骤包括:①圈定一个包含目标研究区的相对完整水文地质单元建立区域模型,避免边界条件的不确定性;②通过区域模型的水均衡运算确定目标研究区的侧向径流补给量和补给层位,计算单宽侧向径流量;③建立稍高精度的目标研究区地下水数值模型,采用计算所得的单宽径流量刻画侧向径流边界,并通过敏感性分析校验目标研究区模型参数准确性和稳定性;④对侧向径流量进行误差分析,评价刻画方法的合理性。
2 研究区地下水数值模型的建立
2.1 研究区水文地质条件概况
研究区位于湖北省钟祥市西北部,汉江西岸,见图1。平原区域受汉江剥蚀-堆积作用影响,形成沿江带状分布的冲积平原,宽度为3~7 km,沿江长度约23 km。冲积平原区地势平坦低洼,地面高程为30~55 m,堆积有第四系全新统(Q4)松散沉积物,组成汉水Ⅰ级阶地,全新统地层至Ⅰ、Ⅱ级阶地交界处逐渐尖灭。第四系全新统地层自上至下分别为:第四系全新统冲洪积层第四系全新统冲积层总厚度约15~30 m。其中具有二元结构,上部为灰黑色河漫滩相黏土、壤土夹淤泥质土,厚度约3~10 m,导水性较差,属弱含水层,下部为黑灰、灰色河床相中粗砂、粉细砂,局部夹淤泥质透镜体,渗透性强于上部,分布连续稳定,平均厚度约9.97 m,是研究区内的主要含水层,见表1。
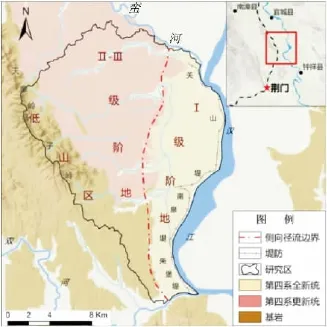
图1 研究区概况Fig.1 Hydrological geology sketch of the study area
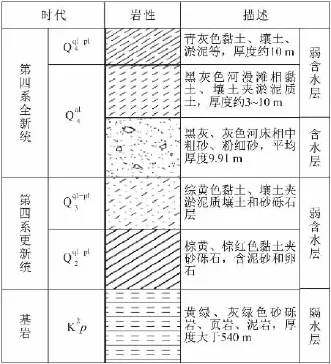
表1 研究区地层一览表Table 1 Stratigraphic and hydrogeological schemes of the study area
研究区以西为汉水Ⅱ、Ⅲ级阶地至低山区,高程为55~420 m,以天摩岭至马子岭一线地势最高,形成研究区西侧地表分水岭,该区主要分布第四系更新统(Q2-Q3)和白垩系跑马岗组(K2p)地层,仅分水岭处出露少量震旦系地层。第四系中上更新统(Q2-Q3)冲洪积物位于全新统下部,出露于靠山侧,组成汉水Ⅱ、Ⅲ级阶地,高程在40~130m之间,主要岩性为黏土、壤土、淤泥质土夹砾石,厚度约10~20 m,含水性和导水性较差;第四系下伏基岩为白垩系跑马岗组(K2p)黄绿、灰绿色砂砾岩、页岩、泥岩,在研究区内分布连续稳定,主要在研究区西南侧局部地区出露,厚度大于540 m,岩性完整且导水性差,是研究区内的隔水底板,见图2。

图2 区域模型和平原区模型结构及参数分区图Fig.2 Structure of the regional and the plain terrain model and parameter sections
区内地下水主要为第四系松散沉积物孔隙潜水,接受大气降水补给,地下水径流方向自西向东,主要排泄于汉江及其支流,少部分以蒸发、植被蒸腾形式排泄,村镇居民点以井形式分散开采少量地下水。汉江是区内最大地表水体,自北向南流经研究区东部,是全区地下水最低排泄基准面。研究区北侧和南侧分别为汉江较大支流蛮河和双河,自西向东汇入汉江。
2.2 数学模型
由于研究区天然条件下地下水位仅随季节性降雨变化,人为扰动小,多年年均地下水水位基本保持不变,因此可以采用稳定流计算研究区地下水多年年均侧向径流量及水位特征。本次地下水数值模型采用非均质孔隙介质三维稳定流数学模型刻画,其数学模型如下:
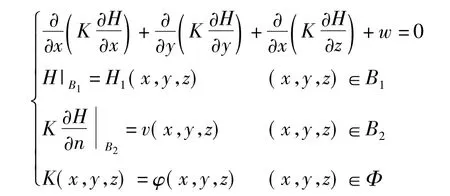
式中:B1为给定水头边界(第一类边界条件);B2为给定流量边界(第二类边界条件);Φ为模型空间;H1为B1边界上已知水头函数;K为渗透系数(量纲为LT-1);w为源汇项(量纲为T-1)为水力梯度在边界法线上的分量。
2.3 区域模型和平原区模型的水量交换
本次目标研究区为汉水Ⅰ级阶地的大部分区域,本文将该目标模型命名为平原区模型,同时提出区域模型的概念,区域模型是指包含目标研究区在内的一个完整水文地质单元作为模拟区的模型。
区域模型的边界主要为大型地表水体和局部地形分水岭,属于数值特征明确的确定性边界,其包含平原区模型,两者共享部分确定性边界。区域模型可以分割为属于平原区模型的Ⅰ级阶地部分,属于低山区和汉水Ⅱ、Ⅲ级阶地的外扩部分。平原区与外扩区的交界线为侧向径流边界,属不确定性边界。区域模型的主要功能在于通过数值法计算模型区的水均衡,获得侧向径流边界处的地下水径流通量和水位,控制总体的水量均衡和边界流量的分配。
平原区模型在满足区域模型水均衡框架的前提下,利用勘察资料对平原区模型内土地利用类型、土壤类型进行细分,细化平原区模型的参数分区,将区域模型中计算的平原区降雨入渗量、侧向径流通量等作为平原区模型的初始参数带入平原区模型,并增加网格剖分数量、剖分密度,通过更加严格的敏感性检验,最终实现嵌套模型的水量转换。
2.3.1 区域模型
区域模型西侧为局部分水岭,东侧为汉江,北侧为蛮河,南侧为双河,面积约302 km2(见图2)。江汉、蛮河、双河三侧边界依据水位观测值设为一类边界条件,其中汉江北部最高水位为44 m,南部最低水位为42 m,沿线采用分段线性插值,平均水力梯度约0.1‰。模型西侧分水岭为零通量边界。
模型三维结构及初始水文地质参数通过勘察资料及气象观测资料确定,见表2。模型垂向结构依据地层含水性,自上往下分为:第四系全新统上部弱含水层(layer1)、第四系全新统下部含水层(layer2)、第四系更新统弱含水层(layer3)、基岩隔水层(layer4)。第四系自东向西逐渐尖灭,layer1、layer2尖灭于1级阶地内,layer3尖灭于II、III级阶地内,山区基岩裸露。模型采用三角剖分,平面上共剖分12 869个节点,最小三角形边长约89 m,模型总共100 636个单元(见表3),模型参数分区按地层含水性区分,见图2(a)、(c)和表2。
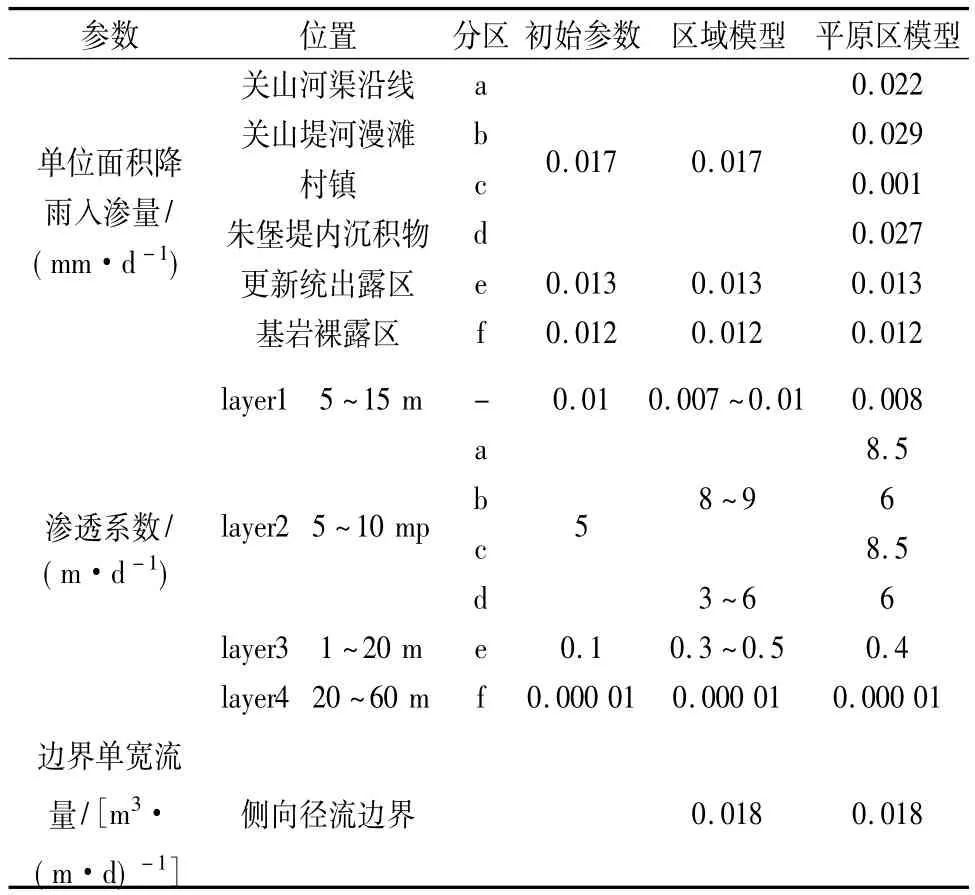
表2 模型参数分区一览表Table 2 Zoning of the model parameters
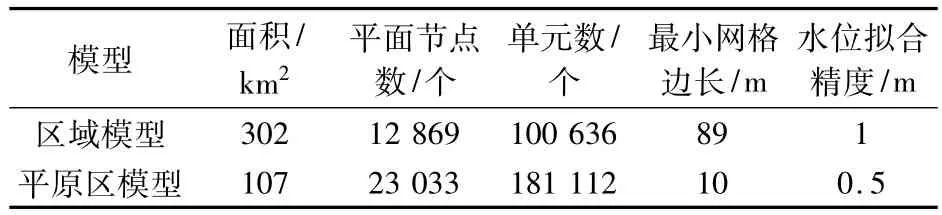
表3 模型剖分及精度一览表Table 3 Mesh condition and precision schedule of the models
区域模型校验采用“试错法”,并进行了上百次运算。拟合结果可靠性的评判依据包括区域流场形态、模型收敛性、水位观测孔拟合数量(观测孔计算水位的置信区间为观测水位上下1m)、拟合精度(RMSE)以及水均衡分析。通过敏感性分析得到参数校验结果见表2中区域模型部分。
区域模型计算的等水位线见图3(a),区域模型模拟结果显示:地下水主要接受大气降雨的补给,以山坡回归流[8]和地下水径流方式向河流排泄。区域模型以侧向径流边界从平面上划分为西部的外扩区和东部的平原区两部分,两部分水均衡将被分别计算。另外,为了分析侧向径流的补给层位,将平原区分割为上覆第四系和下伏基岩,单独计算平原区基岩的水均衡。各均衡区的水均衡项包括:降雨入渗补给量(R)、侧向径流量(q)、边界排泄量(QBC1)、回归流流量(Q回归)。图4显示了区域模型各均衡区的水均衡关系,其中外扩区的降雨补给量中部分以回归流形式排泄于地表水系,其余部分形成地下水径流,以侧向径流(q)形式补给平原区;平原区主要以第四系地层接受地下水侧向径流补给,并接受降雨入渗补给,少量以回归流形式排泄于地表水系,剩余绝大部分以地下水径流形式排泄于河流。侧向径流量q作为平原区补给量考虑,对于外扩区作为排泄量考虑。
各均衡区内均衡项满足如下水均衡关系:
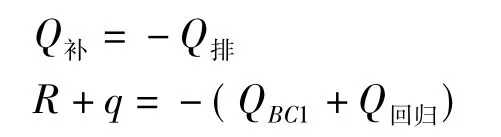
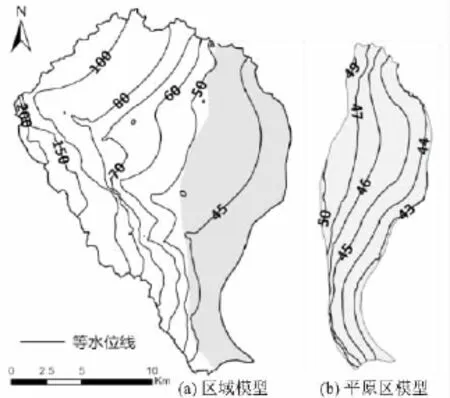
图3 区域模型和平原区模型等水位线图Fig.3 Groundwater level contour of the regional model and the plain terrain model
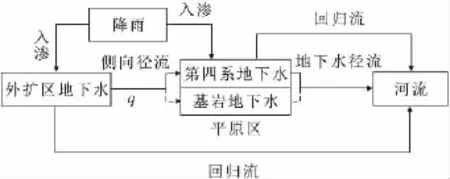
图4 区域模型水均衡流程图Fig.4 Water balance flowchart of the regional model
区域模型水均衡计算结果见表4。由表4计算结果显示,区域模型地下水通过河流(一类边界QBC1)和回归流(Q回归)两种方式排泄。其中,区域模型中回归流主要形成于地形起伏较大的外扩区;平原区地势平缓,主要以地下水径流形式排泄于一类边界(汉江及其支流),平原区侧向径流补给量约为451.2 m3/d,由于侧向径流边界划定在第四系更新统分布区,无全新统的覆盖,因此补给断面主要为第四系更新统地层;平原区基岩地层侧向径流量可忽略不计。
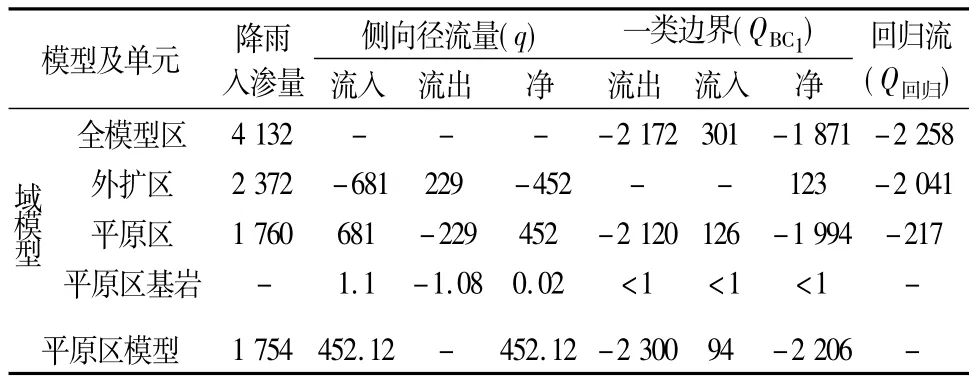
表4 区域模型和平原区模型水均衡计算结果(m3/d)Table 4 Computation result of water balance of the sections of the regional model and the plain terrain model(m3/d)
2.3.2 平原区模型
平原区模型范围与区域模型中计算平原区水均衡的范围一致,三维结构一致,模型面积约107 km2。平原区模型平面上共剖分23 033个节点,最小三角形边长约10 m,模型总共181 112个单元(见表3)。为了提高平原区模型的精度,将区域模型的参数分区进一步划分为关山河渠沿线、关山堤河漫滩、村镇、朱堡堤内沉积物、更新统出露区、基岩裸露区6个子区域,见图2(b)、(c)和表2。细化后的平原区参数分区采用区域模型的参数校准结果为初始值,通过敏感性分析进行微调,可得到最终模型参数校验结果(见表2平原区模型部分)。平原区模型西侧流量边界净流入量取452 m3/d,边界长度为25 250 m,单宽流量约0.018 m3/m·d。
平原区模型侧向径流边界在垂向上包含两类地层(第四系更新统、基岩),通过区域模型水均衡计算已知基岩地层侧向径流量小于1 m3/d,可忽略不计,因此仅将单宽流量赋给第四系更新统断面,并设基岩地层侧向径流量为0。
平原区模型校验方法与区域模型一致,仅将观测孔计算水位的置信区间精确到0.5 m,平原区模型同样进行上百次运算得到拟合结果,见图3(b)和图5。
平原区模型拟合结果显示,平原区模型良好地展现了天然地下水形态,满足了可靠性的评判依据。10个观测孔中8个孔的计算水位误差处于0.5 m的置信区间内,仅2个孔的计算水位(43.09 m、44.87 m)误差稍大(见图5)。平原区模型侧向径流量为452.12 m3/d,与区域模型计算结果基本一致(见表4)。
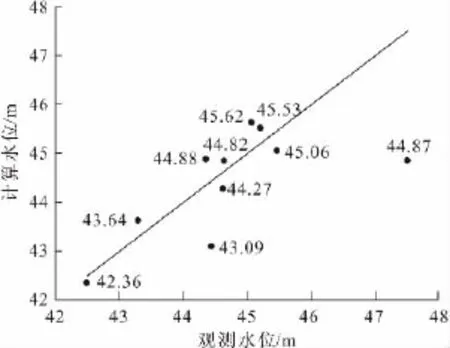
图5 平原区模型水位观测孔拟合结果Fig.5 Calibration result of the observation points of the plain terrain model
2.4 敏感性分析
敏感性分析是确定参数范围、评价参数准确性和模型稳定性的重要步骤[9],本次研究中,区域模型和平原区模型的渗透系数皆通过敏感性分析确定,并以平原区模型的最终拟合结果为准,侧向径流量的误差也通过敏感性分析进行评价。
2.4.1 敏感性分析方法
本文采用均方根误差RMSE(Root Mean Square Error)和平均绝对误差MAD(Mean Absolute Difference)两个参数对模型进行敏感性分析与评价。具体计算方法如下:式中:Hc为观测孔计算水位(m);Ho为观测孔观测水位(m);n为用于校正模型的观测孔数量(个)。
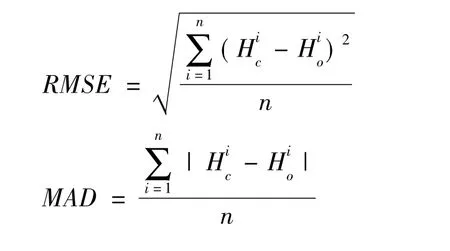
敏感性具体分析过程为:以某个参数矫正结果值为基准,按50% ~150%的比例缩小或扩大单个参数值,计算模型观测孔水位RMSE和MAD的变化,并综合考虑模型流场和两个评价指标的大小,确定参数误差范围。RMSE变化将采用百分比的形式,其变化百分比大于5%,认为该参数对模型影响大,属敏感参数,其变化百分比小于5%,认为该参数不敏感;MAD则采用真值评价。
2.4.2 敏感性分析结果
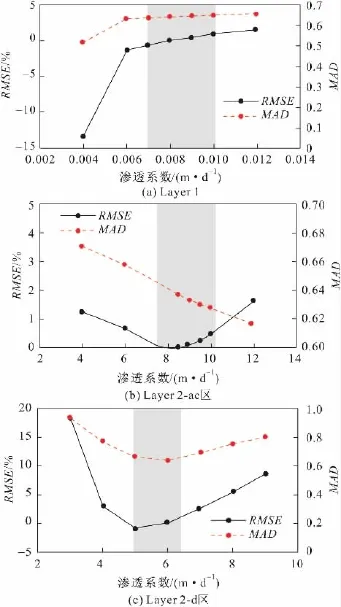
图6 平原区模型地层渗透系数敏感性分析Fig.6 Sensitivity analysis of the hydraulic conductivity of the plain terrain model
平原区模型地层渗透系数敏感性分析结果见图6。由图6可见:平原区模型Layer1地层渗透系数对模型水位精度影响小,对模型误差RMSE产生最大仅1.4%的影响,而MAD变化则更加平缓,渗透系数小于0.007 m/d时会造成模型收敛性显著变差,不予采用,综合考虑渗透系数误差范围在0.007~0.01之间[见图6(a)];平原区模型Layer2-ac区地层渗透系数对模型水位精度影响较小,参数变幅50%仅对模型误差RMSE产生最大1.6%的影响,增大参数能缩小MAD,综合考虑渗透系数误差范围在7.5~10之间[见图6(b)];Layer2-d区地层渗透系数对模型水位影响较大,参数变幅50%可使模型误差RMSE最大增加18.5%,与MAD变化趋势一致,参数较为敏感,应确定更小的误差范围以提高模型精度,考虑到该参数数量级较大,综合分析认为渗透系数误差范围在5~6.5之间[见图6(c)]。平原区模型其余参数对模型的影响不大,综上可见,平原区模型最终参数合理可靠,且数值较稳定。
由于侧向径流量主要通过区域模型确定,并且与区域模型更新统地层的渗透性存在对应关系,因此通过敏感性分析的区域模型,更新统地层参数应该直接用于平原区模型,不予变动。
3 侧向径流量的误差分析
侧向径流量的误差分析可从两个角度说明:其一是区域模型中各参数对侧向径流量的影响;其二是侧向径流量对平原区模型精度的影响。
3.1 区域模型渗透系数对侧向径流量的影响分析
区域模型中侧向径流量的计算与区域模型各地层水文地质参数存在一定的联系。其中,区域模型中更新统地层的渗透性与地下水侧向径流量相关性最强,当更新统地层的渗透性增大 50%(缩小50%),模型RMSE值增加1.1%,侧向径流量增大11%(缩小15%)[见图7(c)];渗透性减小能够减小拟合的RMSE值,但渗透系数小于0.3 m/d时会造成山前地下水位过度抬升,不符合实际水位,因此渗透系数采用0.3~0.5 m/d较为合理,相应侧向径流量在421.1~473.3 m3/d之间。其余地层渗透性对侧向径流量的影响不足10%[见图7(a)、(b)]。
3.2 侧向径流量对平原区模型精度的影响分析
对于平原区模型,以451.2 m3/d为侧向径流量基准,侧向径流量增加或减小5% ~10%对平原区模型观测孔水位仅仅造成RMSE值最大0.2%的变动,侧向径流量变幅为10%~50%使RMSE值最大增加18%,见图8。增加边界流量会显著增大校准误差,这是由于流量增加使东西向水力梯度增大,靠近流量边界一侧的水位明显抬高所造成。综合考虑更新统地层的渗透性范围,侧向径流量在421~473 m3/d以内是合理的。
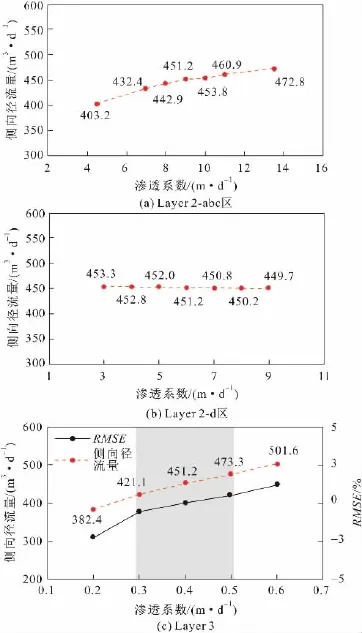
图7 区域模型侧向径流量误差估计Fig.7 Error estimation of the lateral groundwater runoff of the regional model
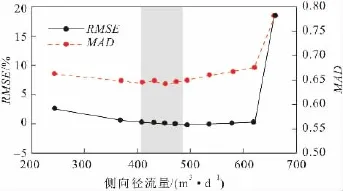
图8 平原区模型侧向径流量误差估计Fig.8 Error estimation of the lateral groundwater runoff of the plain terrain model
4 定水头边界与定流量边界对比分析
一类水头边界和二类流量边界在刻画侧向径流边界过程中存在精度差异性,本次研究中通过侧向径流量反演侧向径流边界处地下水位,以一类水头边界刻画平原区模型侧向径流边界,计算相应边界产生的侧向径流量,并采用敏感性分析相似的统计方法分析一类水头边界的误差范围,其结果见图9。由图9可见,边界水位为48 m时平原区模型RMSE值最小,水位由46 m增加至50 m可使侧向径流量在123.3~1 071 m3/d范围内单调增加,使RMSE值最大增加8%;若平原区地下水侧向径流量在421~473 m3/d范围内,则水头边界水位则在47.9~48.1 m之间。
对比两类边界可以看出,采用流量边界刻画地下水侧向径流边界对模型的稳定性和准确性是有益的。这主要是由于:
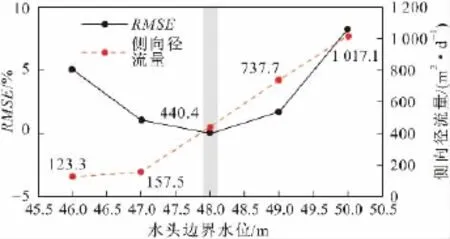
图9 平原区模型水头边界水位与侧向径流量的关系Fig.9 Relationship between water level of the Dirichlet boundary and lateral runoff of the plain terrain model
(1)实测地下水水位用于定水头边界误差较大。实测地下水位受到地形和人工开采地下水的影响,局部地形的高低起伏或人工开采会造成观测水位具有上下数米的变化范围;同时也受到观测孔数量和平面位置分布的影响,如低洼地区钻孔分布较多,计算平均水位就相对较低,通过水位观测孔以插值方法得到的地下水位不能满足0.1 m的精度要求,而误差在0.5 m以上的定水头边界就可能对模型侧向径流量产生数倍的影响。
(2)定水头边界不适用于水位动态变化明显的地下水流场。本次模型采用稳定流计算侧向径流量适用于水位变化不大的天然情况,在水位变幅较大的情况下,如当碾盘山水库蓄水后,侧向径流边界处水位的实际情况将如同图10中②所示,水位上升,过水断面面积增大,水力梯度减小。对于外扩区(剖面AB段),地下水均衡满足下式:
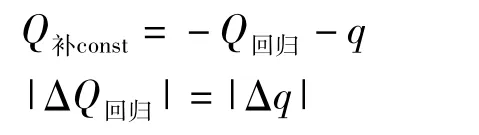
外扩区天然地下水入渗补给量(Q补const)仅与年均降水量相关,由于年均降水入渗量在长时间尺度上变幅不明显,可近似设为恒量[10]。侧向径流(q)和回归流(Q回归)为外扩区主要排泄方式,侧向径流量(q)因排泄受阻稍有减小,则以回归流或蒸发(Q回归)方式排泄量增加,因此侧向径流量减少量与AB段回归流量增加量相等。采用定水头边界刻画侧向径流边界(见图10中①所示),边界处地下水水位将小于实际水位,等水位线看似基本合理,但水头不变造成侧向径流量大幅减小,甚至可能成为平原区的排泄边界,这忽略了水头边界对流量的影响,不符合实际情况。采用定流量边界刻画侧向径流边界基本符合图10中②所示效果,但缺点在于侧向径流量(q)不变,若汉江水位抬升,平原区模型计算水位b可能略高于实际情况。
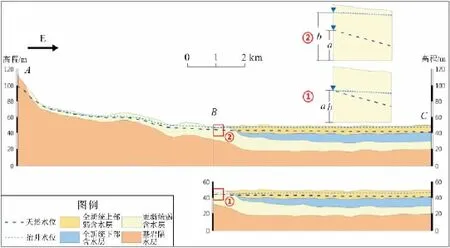
图10 区域模型和平原区模型剖面图Fig.10 Section view of the regional model and the plain terrain model
综上可见,一类水头边界和二类流量边界都同时具有位置特征(水位)和数量特征(流量),该特征对模型边界刻画的合理性具有重大影响。
5 结论与建议
(1)通过嵌套模型水量转换方法研究侧向径流边界,可以深入分析一个完整水文地质单元当中各子系统通过侧向径流边界相互关联的水量、水位特征,既通过刻画区域模型将完整水文地质单元中的地下水流场特征纳入考量,提高了目标区边界条件的精度,又通过精细刻画目标区(平原区)模型,简化了模型结构,提高了模型精度和收敛性、稳定性,具有很强的实践意义。
(2)侧向径流边界多属于不确定性边界,应刻画为二类流量边界,而非一类水头边界。侧向径流边界联系一个完整水文地质单元中的各子系统,子系统之间的水量交换不能保证边界两侧水位一定,在边界处补排不畅、通量稍小,或模拟期内地下水位变幅巨大的情况下,一类水头边界往往不适用。
(3)侧向径流量计算结果与区域模型地层及参数存在对应关系,为确保计算结果正确,应保证模型参数充分校验,并且侧向径流量计算结果带入目标模型也应该对应地层分层赋值。此外,侧向径流量计算结果正确与否可以通过目标模型进行验证。
(4)边界条件除具有双重含义外,还具有双重特征,其一为位置特征,其二为数量特征。一类水头边界主要规定其位置特征(水位),能够接受排泄或提供补给不限量的水量是其数量特征,仅限于刻画补排通畅的大型地表水体;二类流量边界主要规定其数量特征(水量),通过达西定律换算的水量与水力梯度之间定比关系(Q/J=K·A)计算水位是其位置特征。在数值模型的建立过程中,对边界条件的双重含义和双重特征的清晰认识将有助于提高模型的仿真性[11]。
本次研究只涉及目标研究区天然条件地下水,因此采用稳定流计算,但后期碾盘山水库蓄水完成后,地下水动态变化将导致流量边界处水量减少,定流量边界将不能满足精度,此时可结合动态预测方法和嵌套模型水量转换方法,通过区域模型计算动态条件下地下水侧向径流量,并结合地下水观测,调整平原区模型侧向径流量的时间序列。此外,本次研究中区域模型和平原区模型面积比约3∶1,尺度效应造成的误差相对较小,但在区域模型与平原区模型的面积比更大的情况下,区域模型更大的规模误差将削弱侧向径流边界的水量转换精度,而尺度效应对转换精度的影响将有待后续深入的研究。
[1]卢文喜.地下水运动数值模拟过程中边界条件问题探讨[J].水利学报,2003(3):33-36.
[2]沈媛媛,蒋云钟,雷晓辉,等.地下水数值模拟中人为边界的处理方法研究[J].水文地质工程地质,2008(6):12-15.
[3]任立良,刘新仁,郝振纯.水文尺度若干问题研究述评[J].水科学进展,1996(S1):87-99.
[4]刘永林,胡斌,刘智权,等.基于GMS的浸没几何影响因素分析[J].工程勘察,2011,39(8):60-64.
[5]连志鹏,谭建民,闫举生,等.库水位变化与降雨作用下库岸斜坡稳定性分析[J].安全与环境工程,2011(2):14-17,22.
[6]Peleg N,Gvirtzman H.Groundwater flow modeling of two-levels perched karstic leaking aquifers as a tool for estimating recharge and hydraulic parameters[J].Journal of Hydrology,2010,388(1/2): 13-27.
[7]Weiss M,Gvirtzman H.Estimating ground water recharge using flow models of perched karstic aquifers[J].Ground Water,2007,45(6): 761-773.
[8]芮孝芳.水文学原理[M].北京:高等教育出版社,2013.
[9]钱会,王毅颖,宋秀玲.地下水流数值模拟中不应忽视的几个工作程序[J].勘察科学技术,2004(1):40-43.
[10]高寅堂.对平原区山前侧向径流量几个问题的浅析[J].地下水,1990(1):21-23,20.
[11]陈崇希.“防止模拟失真,提高仿真性”是数值模拟的核心[J].水文地质工程地质,2003(2):1-5.
Study on Characterization Methods of Groundwater Lateral Flow Boundary Condition Based on the Nested Model—A Case Study of Groundwater Numerical Simulation of Nianpanshan Alluvial Plain in Hubei Province
WANG Zhenchen1,CHEN Zhihua1,XU Dong2,PENG Kang1
(1.School of Environmental Studies,China University of Geosciences,Wuhan430074,China; 2.School of Environmental Science and Engineering,Ocean University of China,Qingdao266100,China)
Lateral flow boundary condition is a key issue in numerical simulation of ground water.Taking Nianpanshan hydropower project in Hubei as an example,based on the finite element method and the water transformation of the nested model,this paper sets up a regional model which contains a complete hydrogeological unit and a plain terrain model which only covers theⅠlevel terrain of Han River.Through water balance calculation in different sections of the regional model,the paper confirms the flux of the lateral flow boundary.Then,in the regime of the regional water balance,the paper establishes the plain terrain model respectively with the lateral flow boundary depicted by the Dirichlet boundary condition and the Neumann boundary condition.Next,the paper analyzes the relationship between the two models both in model parameters and water transformation relations,and compares the pros and cons and applicable conditions between the two kinds of boundary conditions in depicting lateral flow boundary.The result shows that accurate lateral groundwater runoff can be calculated by using the nested model,and using Neumann boundary condition depicting lateral flow boundary is helpful to improve accuracy and stability of the plain terrain model.It is concluded that the boundary condition has dual-characteristics along with the dual-meaning.In the process of building models,the position characteristics(water level)and the quantity characteristics(water volume)should be fully recognized.
groundwater;lateral flow boundary;numerical simulation;nested model;water balance
X143;P333.1
ADOI:10.13578/j.cnki.issn.1671-1556.2016.05.004
1671-1556(2016)05-0020-09
陈植华(1956—),男,教授,博士生导师,主要从事地下水科学方面的教学与科研工作。E-mail:zhchen@cug.edu.cn
2016-04-07
2016-08-07
湖北碾盘山水利水电枢纽工程浸没问题地下水数值模拟专题研究项目
汪祯宸(1988—),男,硕士研究生,主要研究方向为地下水数值模拟。E-mail:wzc20060811@163.com

