影像处理刀具测量仪的误差补偿
赫 野, 张 伟, 贺 凤 宝, 胡 建 忠
( 大连工业大学 机械工程与自动化学院, 辽宁 大连 116034 )
影像处理刀具测量仪的误差补偿
赫 野,张 伟,贺 凤 宝,胡 建 忠
( 大连工业大学 机械工程与自动化学院, 辽宁 大连116034 )
摘要:绝对零点的选择是误差分析和补偿的基础,通过对测量仪自身特点的分析,选择带有零位参考点的光栅尺确定补偿系统的绝对零点,消除原有绝对零点中人为因素所造成的影响,使得采集的数据点更加精确可靠。利用分段三次样条插值函数将离散数据点处的误差值由离散性插值变为连续性,以软件编程的方式将误差值从实测数据中除去,使得输出的数据更加精确。通过补偿实验验证了绝对零点选择的合理性,提高了测量仪测量精度和产品的市场竞争力。
关键词:误差;绝对零点;插值函数;补偿

0引言
机械设备的精度不仅是实现精密加工和超精密加工以及精密测量的前提, 更是衡量其工作性能的重要指标[1]。目前要提高仪器精度有两种方法,分别为防止法和误差值补偿法[2]。防止法采用的是通过提升仪器的硬件精度来提高仪器的测量精度,该方法存在的缺陷是当硬件精度达到一定程度后很难再提高,并且成本造价可能会以几何倍数增长。误差值补偿法是在取得原始误差值后,从整个系统的硬件设施和程序软件两个方面着手消除原始误差所造成的影响,提高仪器的测量精度,此方法既经济又有效,更适合市场的发展需求。
由于测量仪器出厂前硬件的安装和调整已经完成,在后续测量过程中所产生的误差将由误差补偿来完成。本论文是在前人对刀具测量仪误差分析[3]的基础上,以大连工业大学刀具技术研究中心开发的基于影像处理刀具测量仪为实验仪器,在尽量少增加额外硬件的基础上,在X和Y两坐标轴有效量程范围内采集大量离散的数据点,算出每个数据点处的累积误差值,最后通过误差补偿的方法将误差值补偿到测量程序中,提升仪器的测量精度。
1误差补偿
1.1误差补偿工作流程
误差补偿工作流程如图1所示。
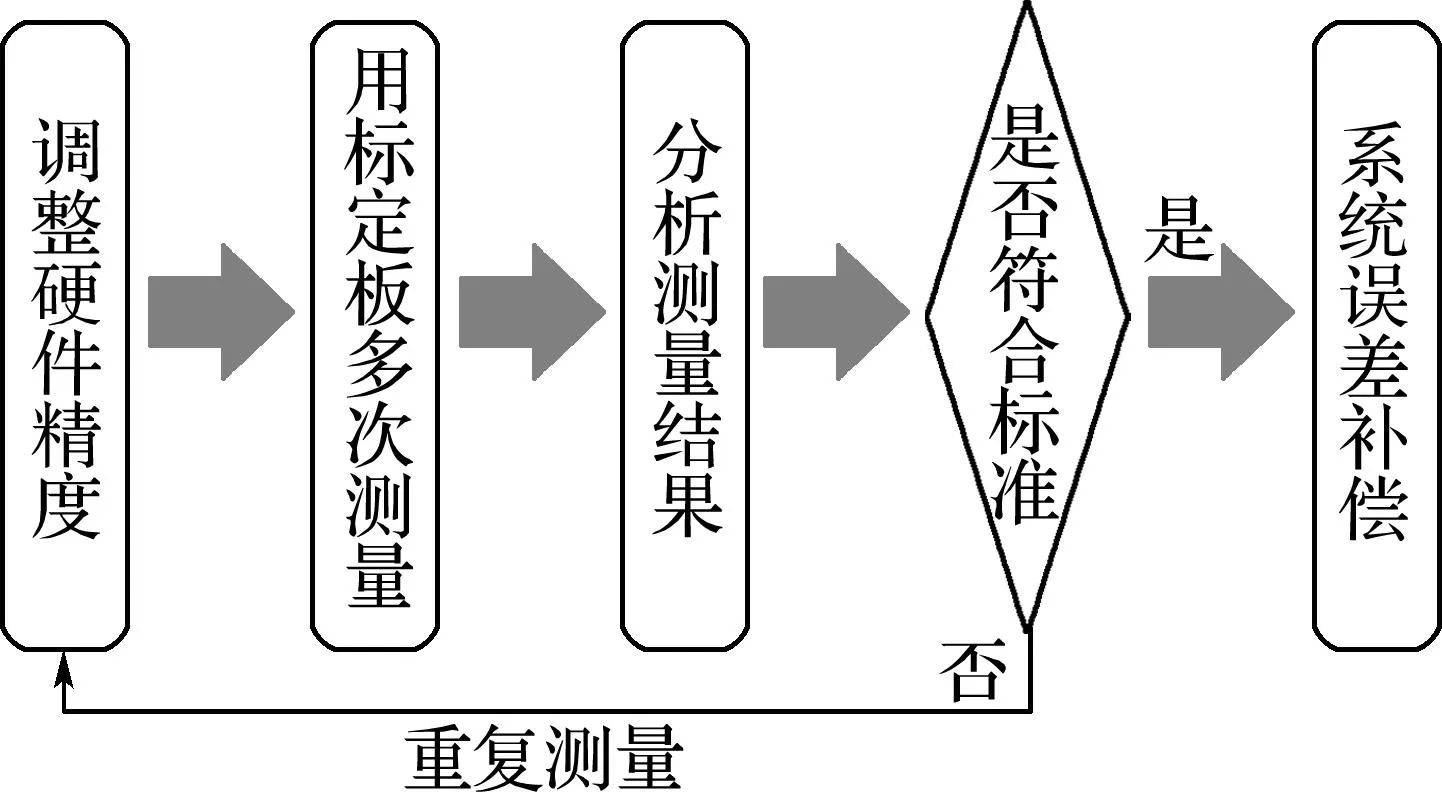
图1 工作流程图
1.2绝对零点的选择
数控机床中各坐标轴的零点,一般分程序零点和机床零点,或者叫相对零点和绝对零点[4]。在现代机床补偿技术上选择出科学准确的绝对零点是机床精度补偿中重要的部分,同时这也是误差补偿的基础,如果没有绝对零点,补偿工作无从谈起[5]。因此绝对零点精度的高低直接影响接下来的误差补偿工作。
测量系统原有绝对零点是在V型铁上钻直径为3 mm的盲孔(见图2),通过十字光标刻线外切盲孔边缘的方式来确定绝对零点。由于是靠人眼视觉来确定,因此人为因素所造成的影响是避免不了的。本次补偿工作选择带有零位参考点的光栅尺和能识别零点信号的光栅采集卡来确定补偿系统的绝对零点。

图3为X轴光栅尺,总共设有5个零位参考点,当光栅尺读数头每经过一个零位参考点时会产生一个零位脉冲信号,该信号由数据采集卡识别并反馈到系统中。但是原有测量系统中并不存在读取以及使用该信号的功能,因此需要编译相应的零点识别程序。绝对零点控制窗口如图4所示,补偿工作开始时选择<打开>功能,这样光栅尺读数头每经过一个零位参考点就会识别该零位信号并清零,当确定选择其中某个零位参考点作为绝对零点后,激活<关闭>功能,此时刚刚经过的零位参考点就是选择好的绝对零点,读数头再经过其他零位参考点就不再有清零功能。通过验证该绝对零点的重复性精度可达1~2 μm,并且稳定性好,消除了人为因素所造成的影响,确保后续采集数据的准确性。

图3 X轴光栅尺
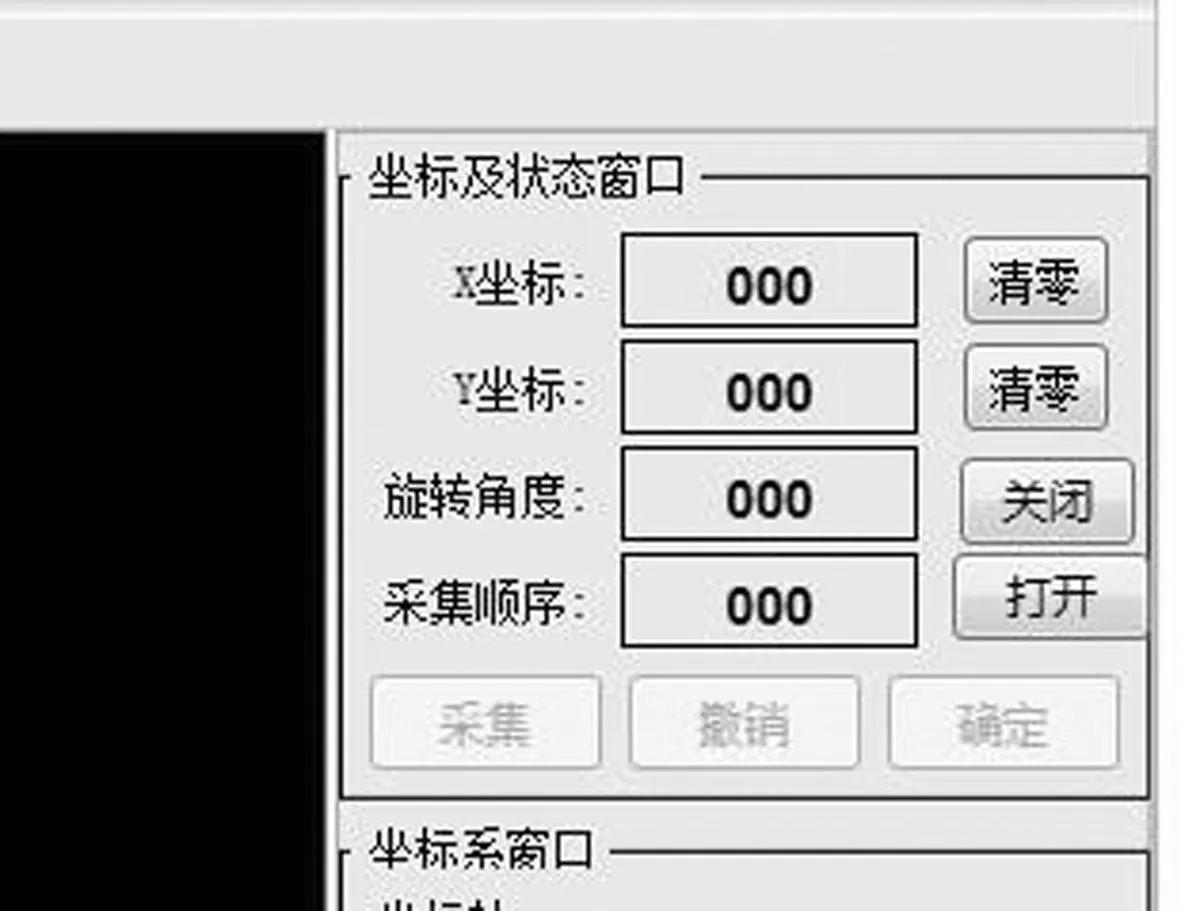
图4 软件截图
1.3实验数据采集
通过设计的模板微调夹具调整好棋盘格标定板与镜头视线的垂直度,选择绝对零点,然后开始实验数据采集,采集过程由三个人进行,分别对X和Y两坐标轴的正负方向进行数据采集,总共12次,根据长度的不同在X轴和Y轴方向上分别采集60个和27个离散数据点,去除粗大误差,求得每个数据点处的累积误差,用MATLAB软件绘制累积误差趋势图。以X轴正向为例,如图5所示,累积误差随着工作距离的增加而增大,在180 mm量程范围内累积误差最高达到了0.04 mm,0.04 mm 的误差已经满足不了测量精度,因此通过后续误差补偿来解决。
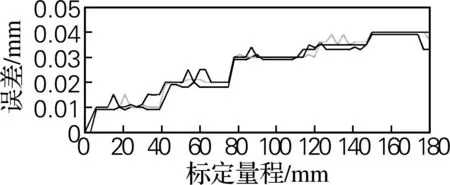
图5 X轴正向误差
1.4补偿方法的选择
在对影像处理刀具测量仪进行补偿中,由于已经拥有测量仪整套的测量软件和程序,并且收集了X轴和Y轴大量的离散数据点,通过数据分析处理后得到了每个数据点的误差值,但是这些数据点之外的数据点误差未知,插值函数能够满足这个要求,将离散变量“联成”连续变量[6]。其中分段3次样条插值函数具有逼近曲线光滑、稳定性好的特点,因此本次补偿采用分段3次样条插值作为补偿函数,将误差直接补偿到程序中去。
以X轴正向采集数据为例,用[0,180]量程范围作为插值区间,区间内总共选取了60个数据点作为分段3次样条插值函数的插值节点,插值步长为3 mm,通过3次插值多项式
S(x)=ci1(x-xi)3+ci2(x-xi)2+ci3(x-xi)+ci4
对任意两个插值节点间的数据进行误差补偿。其中x为光栅尺当前位置时的坐标值,xi为x前面的插值节点,S(x)为当前位置处光栅尺的累计误差,记为Δ,那么通过补偿后显示在屏幕窗口处的输出值S=x-Δ。插值后的曲线见图6。
图6 插值曲线图
2对比实验
2.1误差补偿前后
如图7所示,对比误差补偿前180 mm量程范围内累积误差算数平均值达到了0.037 mm,且误差趋势随着工作距离的增加而增大,误差补偿后的累积误差值在1~4 μm上下波动,总体来说趋势趋于稳定,补偿效果明显。
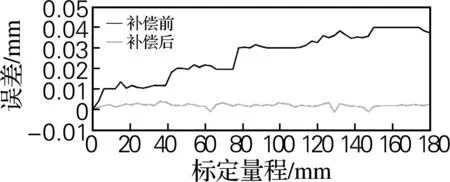
图7 量程补偿前后对比
2.2误差补偿前后100 mm量块测量对比
标定补偿实验后对长度为100 mm的量块分别进行10次测长数据采集,并将此数据与标定补偿前的10次数据作对比见表1所示。由表1可以看出,误差补偿后误差值波动范围比误差补偿前小,在将10次测长值取平均值后,补偿后的平均值更接近100 mm量块的长度,补偿前累积误差平均值为-0.001 9 mm,补偿后为-0.000 2 mm,由此可见补偿效果明显。


表1 实验测量数据
3结论
通过误差补偿实验,证明了绝对零点选取的合理性以及分段3次样条插值函数在补偿计算中的可行性。
通过误差补偿,使得X和Y两坐标轴有效量程范围内的累积误差大幅度降低,且两坐标轴的累积误差值由线性增长变为在一定范围内的平稳波动,使测量仪在整体上提升了测量精度,提高了产品的市场竞争力。
参考文献:
[1] 范晋伟,杨万然,陈文,等.数控机床几何误差补偿器的实验研究[J].机械设计与制造,2009(2):160-161.
[2] 兰通联.提高数控机床改造精度方法探讨[J].现代商贸工业,2009(16):281-282.
[3] LEE J H, LIU Y, YANG S H. Accuracy improvement of miniaturized machine tool:geometric error modeling and compensation[J]. International Journal of Machine Tool and Manufacture, 2006, 46(12/13): 1508-1516.
[4] 高世春,王兆吉,张伟.数控机床的零点定位方法[J].大连轻工业学院学报,1997,16(1):36-38.
[5] 赵耀.DJCLY92B刀具几何参数测量仪误差分析与精度补偿[D].大连:大连工业大学,2010:13-14.
[6] 薛定宇,陈阳泉.高等应用数学问题的MATLAB求解[M].北京:清华大学出版社,2004:325-332.
Error compensation of image processing based on cutting-tool measuring instrument
HEYe,ZHANGWei,HEFengbao,HUJianzhong
( School of Mechanical Engineering and Automation, Dalian Polytechnic University, Dalian 116034, China )
Abstract:Because choosing absolute zero was the basis of error analysis and compensation, the characteristics analysis of instrument itself and the system compensation of absolute zero by grating with zero reference point could eliminate human factors to collect data point more accurately and reliably. The output data was more accurate when using piecewise cubic spline interpolation function to become error value of the discrete data points from discrete to continuous interpolation and removed the error value from the measured data by the way of software programming.
Key words:error; absolute zero; interpolation function; compensation
作者简介:赫 野(1987-),男,硕士研究生;通信作者:张 伟(1962-),男,教授.
收稿日期:2014-06-06.
中图分类号:TH71
文献标志码:A
文章编号:1674-1404(2016)01-0076-03

