立足课堂，积累数学活动经验

杨文杰++郑燕燕

摘 要：数学基本活动经验是《义务教育数学课程标准（2011年版）》提出的课程目标中的“四基”之一，也是数学课程的重要内容组成部分。课程目标由“双基”转向“四基”，引起了很多数学教育工作者的思考。在数学学习中，要使学生真正理解数学知识，感悟数学的理性精神，就应该让学生体验丰富而有效的数学活动，积累数学活动经验。

关键词：活动经验；激活；积累；提升

数学活动经验是学习者在数学活动中形成的感性知识、情感体验和应用意识。它无法用语言或者文字进行格式化，因此不能直接通过教师传授获得，而要在“做”的过程和“思考”的过程中沉淀，是在数学活动过程中不断积累的。它不仅让学生亲身体验整个数学学习过程，实现了以学生为主的生本课堂，而且他们自主掌握了基本知识和基本技能，获得基本的数学思想和方法，提高自身的数学素养。

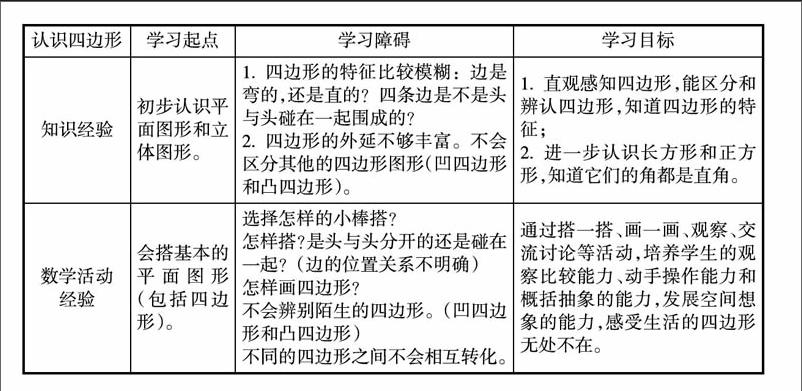
学生数学的学习受已有活动经验的影响。作为教师，我们是经验的改造者、促进者，应该分析原有活动经验的形成因素。活动经验的形成分先入为主的日常生活经验，比如说“高”是从上而下的垂线；经验的负迁移，例如乘法的分配率与乘法的结合律25×（4+2）=25×4+25×2；已有活动经验的局限性还有词语本身带来的曲解（平行线）……这些已有的经验将会制约新活动经验的发展。受新课程教学理念趋势的影响，《义务教育数学课程标准（2011年版）》课程目标指出：“通过数学学习，学生能获得适应社会生活和进一步发展所必需的数学的基础知识、基本技能、基本思想、基本活动经验。”把基本活动经验作为四基要求之一，引起了数学教育工作者的高度重视。下面笔者以“四边形的教学为例”，分析这节课学生的学习起点，在学习中学生碰到的一些障碍，以及要达成的学习目标。如表：

根据以上分析，笔者从把握学生起点，激活原有活动经验；注重课堂操作，积累数学活动经验；感悟数学思想，提升数学活动经验三个方面进行阐述：

■一、把握学生起点，激活原有活动经验

学生的学习起点是指学生在当前状态下已有的四基起点（包括知识起点、技能起点、经验起点和数学思想起点的总和）。我们的教学要达成哪些教学目标，必须先分析学生的起点在哪儿？着眼于学生的最近发展区。课前老师可以通过访谈法，或者设计学习单了解学生已经会了什么，也可以上课开门见山找起点。基于学生学的经验准备一些丰富的、富于生活原型的、具有可操作性的实践活动，如看一看、搭一搭、数一数、找一找、想一想等一系列数学活动，来激活学生的原有活动经验，提高学生的学习积极性。

【片段回放】

环节一：搭四边形——感悟四边形的意义

1. 揭题：今天我们一起来认识四边形。（板书课题：四边形）

2. 搭四边形。

a. 想一想，搭一搭。心里想一个四边形，回忆它是怎样的一个四边形。

b. 小组合作搭四边形，教师巡视选择代表性的作品。（长方形、正方形、平行四边形、梯形）

c. 观察这些图形，是四边形吗？说说理由。（是四边形）

d. 指着图形数一数4条边。（板书：4条边）

3. 进一步认识四边形。

a. 介绍四边形的搭法；

b. 补充四边形的概念。

【分析】

1. 把握学生起点，需设计有效的数学活动

如何来设计有效的数学活动呢？首先要分析学生的起点在哪儿？学生去哪里？需要设计哪些活动来激活原认知。认识四边形是在学生初步认识立体图形和平面图形的基础上进行教学的。学生在生活中已经认识了“模糊”的四边形。模糊在哪儿？大多数学生能知道四边形有4条边，至于头与头碰在一起，相互不分开围成的四边形，需要在搭的过程中观察讨论建构四边形的正确模型。所以笔者设计以下有效的数学活动：先让学生想一想，四边形是怎样的图形？其目的在于唤醒学生的原有知识经验，四边形有四条边。接着根据这条信息让学生选择4根小棒搭一搭，完成后让学生观察四边形是用了几根小棒，再通过数一数的活动对边的数量进一步地确认，最后让学生上台实物演示搭，边搭边介绍方法。这些数学活动经过学生想象、动手操作、充分观察、全班的交流讨论，不仅激活了原有活动经验，而且丰富了学生对四边形的认识。

2. 把握学生起点，需设计启发性的数学问题

《义务教育数学课程标准（2011年版）》提出：学生是学习的主体，教师是学习的组织者、引导者与合作者。在数学教学活动中，教师应该激发学生的学习兴趣、调动学生的积极性，引发学生的数学思考。教师需设计一些赋予启发性的问题，既能呼唤起学生的原有知识经验，还能引发学生深入的思考。比如说教师首先提出：想一想，什么样的图形是四边形？一方面可以了解学生对四边形的认知有哪些，另一方面也可以暴露出学生的错误想法。接着“你是怎样搭起来的？”“像这样分开可不可以？”一系列的问题让学生对四边形的认识有了更清楚的认识，四边形除了四条边，还需要头与头碰在一起围成。教师富有启发性的问题可以引发学生对四边形深入的观察和思考，通过举反例、讨论来消除，逐步建立正确的四边形模型和丰富的活动经验。

■二、注重课堂操作，积累数学活动经验

【片段回放】

环节二：画四边形——理解四边形的特征

1. 引入：我们通过搭小棒的活动认识了四边形。把你心里想的四边形画在小方纸上，一张纸画一个图形，比一比谁画四边形又快又多。

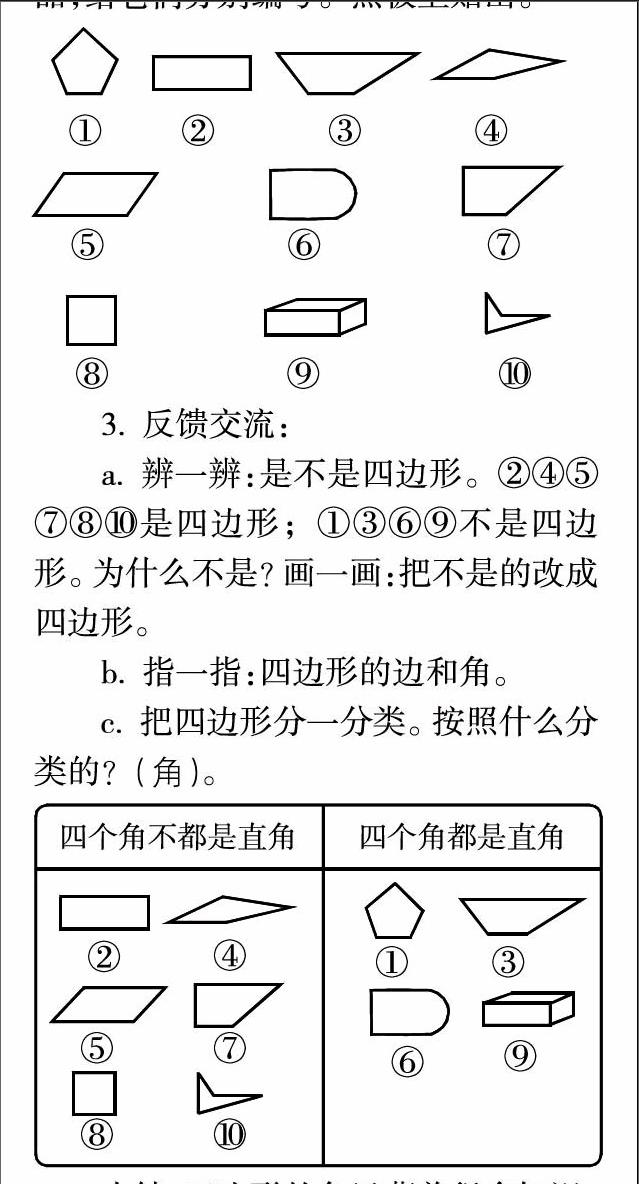
2. 展示交流：这是老师收集的作品，给它们分别编号。黑板上贴出。

■

3. 反馈交流：

a. 辨一辨：是不是四边形。②④⑤⑦⑧⑩是四边形；①③⑥⑨不是四边形。为什么不是？画一画：把不是的改成四边形。

b. 指一指：四边形的边和角。

c. 把四边形分一分类。按照什么分类的？（角）。

■

小结：四边形的角里藏着很多知识，像长方形、正方形这样四个角都是直角的四边形是特殊的四边形。

d. 观察这么多四边形，思考它们有什么相同的特征。

小结：四边形都有4条直的边和4个角。

【分析】

课堂操作活动包括直观的动手操作和隐性的思维操作活动。动手操作是小学数学课堂教学中的一种重要的学习方式，它能有效地解决数学高度抽象性与小学生思维具体形象性之间的矛盾，更重要的目的是帮助学生建立抽象思维与形象思维能力之间的直通桥，帮助学生建立表象。学生的数学知识不是老师教会的，是自己悟会的。学生要在不断的数学学习活动中积累活动经验，学生经历什么样的数学活动，在学习过程中就积累什么样的数学活动经验。这些数学活动形式化之基础知识，经验化之基础技能，概括归纳之数学基本思想。体验动手操作活动，要把这种“经历”形成并积累“经验”。

1. 观察、想象、操作，积累直观表象经验

小学阶段的几何图形教学中，操作、观察、想象等活动常常是重要的学习方式。《认识四边形》是一节操作性很强的课。第二个环节中，安排了第一个活动画一画：学生通过搭四边形活动探究竟怎样的图形叫四边形，借助想象四边形的特征，画出四边形。学生对四边形的建构程度不同，画出来的图形正确率和数量也不同，这些课堂生成性的资源不仅为学生提供了丰富的学习材料，而且为教师后继教学选择如何教学措施提供了信息。第二个活动指一指边和角，特别是⑩号凹四边形学生很少接触过，让学生上台指一指它的四条边、四个角，让学生感悟四边形的特征。第三个活动分一分，你是按照什么分的？让学生体会长方形和正方形是特殊的四边形。最后是观察活动，找一找有什么相同点，抽象出了数学的本质，四边形有四条边四个角。这些层层递进的数学活动，有利于学生积累直观操作经验，学生的思维也从肤浅走向深刻，提升了思维力度。

2. 辨析、概括、归纳，积累数学思考经验

直观的操作活动帮助学生建立事物的表象，要把这些活动形成技能，通过语言表达来调节，整理自己的思维活动，使之逐步完善，形成技能。为了了解学生的思维活动情况，我们可以把点名发言、小组交流、和同桌对讲等不同方式结合起来，使学生都有口头表达的机会，倾听学生的表达，发现学生操作、思维过程中的闪光点与存在问题，给予肯定与纠正。这节课的闪光点就是教师运用了辨一辨的学习方式，说一说哪些是四边形，哪些不是四边形。在学生交流讨论中深化对四边形特征的认识，抓住了四边形的本质特征，去除非本质的概念。最后学生进行自主小结，提升了学生的数学思维。可见，辨析、概括、归纳的教学方式可以积累学生的数学思考经验。

■三、感悟数学思想，提升数学活动经验

【片段回放】

环节三：再搭四边形——感悟四边形的应用性和灵活性

（1）想一想：刚才我们搭了四边形，研究了四边形的特点，现在请你找一找在这幅校园图中的四边形。

（2）现在老师要请你搭四边形，请同学们听仔细：选择两根黄色的小棒和两根蓝色的小棒。用这4根小棒，搭四边形。同桌两人合作完成。

教师先展示四边形的4种情况，然后小结同样的四根小棒可以搭出四种不同的四边形。

（3）教师：我们可以用这四根小棒搭出这么多形状不同的四边形。

a. 重点研究长方形与平行四边形的区别。

b. 凹四边形和凸四边形之间的转化。

【分析】

《课程标准（2011年版）指出：“数学思想蕴含在数学知识形成、发展和应用的过程中，是数学知识和方法在更高层次上的抽象与概括。其中最基本的数学思想是抽象、推理、模型。

反之，感悟了数学思想，提升数学活动经验。在巩固练习环节，教师设计如下两道习题：

1. 在生活原型中找四边形。数学来源于生活，最后还是应用于生活，用举例的思想找出形状不同、大小不同、颜色不同的四边形，其实质是相同的。

2. 开放性的操作活动，选择两根黄色的小棒和两根蓝色的小棒，用这4根小棒搭四边形。根据角的特征，出现了长方形和平行四边形，还有凹四边形和凸四边形。这个数学活动蕴含着变中不变的数学思想，变的是四边形的形状，不变的是四边形的本质。凹凸四边形之间的相互转化沟通了几何形体的内在联系，以旧知引新知，适时归类，形成知识体系，促进学生数学思维，发展其空间观念。在操作中感悟，在感悟中提升了数学活动经验。在开放性的操作活动中，丰富了四边形的内涵，但揭示了不变的四边形的本质特征。

总之，数学活动经验的积累需要一个长期的过程，因此，教师要转变教学观念，要以学生的经验为基础，在学生如何去的路中，让学生不断地经历各种数学活动，在活动中触类旁通，积累丰富的、有价值的数学活动经验。