不同高度开洞对高层建筑风特性影响的数值模拟

夏祥忠，陈锐林，任海龙，胡 迪，邓小波，张 超

(湘潭大学土木工程与力学学院，湖南湘潭411105)

不同高度开洞对高层建筑风特性影响的数值模拟

夏祥忠，陈锐林，任海龙，胡 迪，邓小波，张 超

(湘潭大学土木工程与力学学院，湖南湘潭411105)

采用RNG的k-ε湍流模型，对处于B类地貌风场中的不同高度处设置洞口的高层建筑进行数值模拟，通过UDF编程设定风速和湍流强度等参数。结果表明：当洞口位于0.85h高层建筑时，风速在迎风面前方减弱，在侧面增大并形成对称涡旋，在背风面形成尾流；洞口内形成狭缝效应风速最大；当洞口位于不同位置时，洞口对迎风面和侧面风压以及顺风向基底弯矩都有影响；洞口位于0.65h时,侧面风压系数较小,基底弯矩降幅最大，因此在0.65h开洞最为有利。

k-ε湍流模型；开洞高层建筑；风压特性；计算流体动力学；数值模拟

随着城市高层建筑物不断的涌现，风荷载也成为设计主要考虑的因素。由于建筑外形日益多样化，高层建筑开洞也越来越多，洞口一方面对建筑物表面的风压产生影响，另一方面可以利用其进行发电。自Davenport[1]于上世纪60年代提出风振理论以来，关于高层建筑风荷载的研究迅速开展，逐步形成了较为成熟的理论和计算方法，各国风荷载规范得以出现[2-5]。Kwok等[6]对水平双向开洞的CAARC(Commonwealth Advisory Aeronautical Research Council)模型进行的风洞试验，表明双向开洞能减小建筑物顺风向风荷载。Kikitsu等[7]进行了高层建筑气动响应的风洞实验，结果表明：开洞在相应的区域能影响建筑物的气动力特性。张耀春等[8-9]通过风洞试验和数值模拟对静风作用下的开洞高层建筑进行研究，发现建筑物的开洞方向和风速在同一方向时，作用在建筑物上的静风荷载会减少，但局部区域的风压有所增加。李秋胜等[10-11]探讨在洞口处设置风机对结构风荷载的影响和设置洞口进行风力发电的可行性，结果表明风机增加基底反力，洞口可以对风速进行放大，这对风力发电比较有利。

本文以处于B类地貌风场中的高层建筑为研究对象，探讨在0.85h(h为建筑物高度)处设置洞口时高层建筑洞口周边和洞口内的风场以及立面的风压特性，并研究不同开洞位置建筑物的风压特性，以供相关研究和工程设计参考。

1 模拟计算

采用Fluent 6.3软件进行数值模拟。

1.1 计算模型

建筑物的尺寸长(X)×宽(Y)×高(Z)为30 m× 30 m×180 m，并在建筑物的表面设置一个15 m(Y)× 15 m(Z)的洞口，开洞率为4.2%。计算域(数值风洞)尺寸为1 200 m(X)×600 m(Y)×450 m(Z)，建筑物置于流域沿流向接近1/3区域处即计算模型距离计算域入口400米，阻塞率为2%。计算域边界面和建筑物表面采用三角形非结构网格单元进行离散，体网格采用四面体单元进行划分。建筑物和计算域三维图见图1。

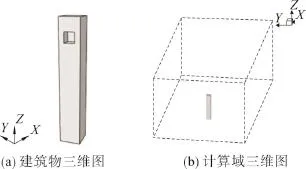
图1 建筑物和计算域三维图Fig.1 Three dimensional building model and computational domains

1.2 边界条件

计算区域进流面选用速度入口(velocity inlet)，来流为我国荷载规范中的B类地面粗糙度剪切流，平均风速剖面为

式中：Z0为标准参考高度；U0为标准参考高度处的平均风速；Z为任一高度；U(Z)为任一高度处的平均风速，α为地面粗糙度指数，我国规范B类地面粗糙度α=0.16。

来流湍流流特性通过直接给定湍动能k和湍流耗散率ε值的方式给出

式中：l为湍流特征尺度；I为湍流强度，因为我国建筑荷载规范没有定义湍流强度I，所以对B类地貌湍流强度进行模拟时参考日本规范第∏类地貌的值。

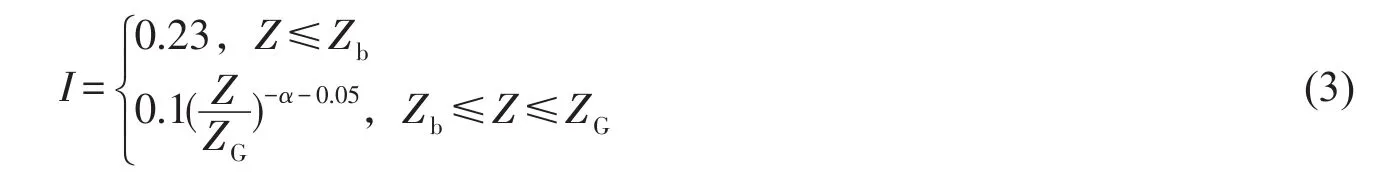
式中：Zb=5 m；ZG=350 m；α=0.15。

本文采用RNGk-ε模型，在入流面用湍动能和湍流耗散率定义，入流面设定为速度入口边界条件，出流面设定为压力出口面。入流边界条件的平均风速剖面U(Z)，k和ε采用UDF(User-Defined Function)编程连入Fluent软件中，出口边界条件采用完全发展的出流边界条件(outflow)，对于计算域顶面和两侧采用自由滑移的壁面为对称边界条件(symmetry)，建筑物表面和地面采用无滑移的壁面条件(wall)。使用有限体积法对控制方程进行离散，用3D分离式求解器隐式算法对控制方程求解，对流项使用精度较高的二阶迎风格式进行离散，速度压力耦合采用SIMPLEC算法[12]。大气层中的流体为定常流，流体介质为空气，具有低速和可压缩性，空气的密度为1.225 kg/m³。计算中使用自适应网格，每步迭代对压力梯度大的区域进行网格加密。计算的迭代残余量设置为5×10-4，风压值趋于稳定时，则流场的计算完成。

2 UDF验证及洞口在0.85h处的风特性分析

2.1 UDF验证

为了验证UDF的正确性，在入流面沿高度布置测点主要对速度和湍流强度进行验证，同时和理论值进行比较，结果见图2，3。图2表明UDF编程输入的风速随高度变化曲线与理论值基本一致，验证UDF编程中速度的正确性。 图3表明UDF编程输入的湍流强度与理论值除了底部有稍微偏差其余基本相同，验证了UDF编程中湍流强度的正确性。

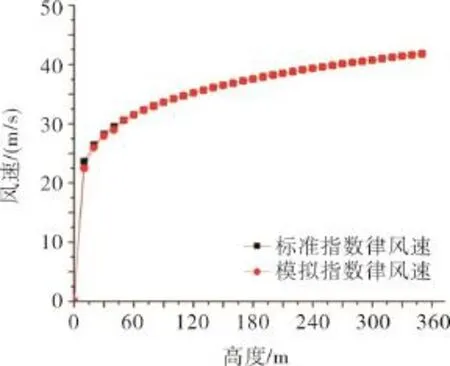
图2 入流面风速随高度变化曲线Fig.2 Curve of wind speed with height in the in flow surface

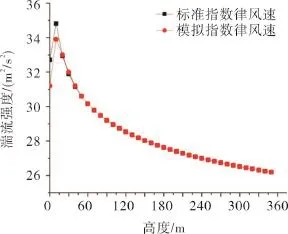
图3 入流面的湍流强度随高度变化曲线Fig.3 Variation curve of turbulent intensity of the flow surface along with the height

2.2 风速分布

数值模拟能很好地模拟建筑物周边的风场，选择洞口在0.85h处的建筑物，通过截取Z=153 m剖面(建筑物洞口的中心高度为153 m)，Y=300 m剖面和在洞口内设置测点来分析开洞高层建筑风速的特点。图4，5分别为Z=153 m剖面、Y=300 m剖面风速分布。

图4 Z=153 m剖面风速分布Fig.4 Distribution of wind velocity atZ=153 m profile

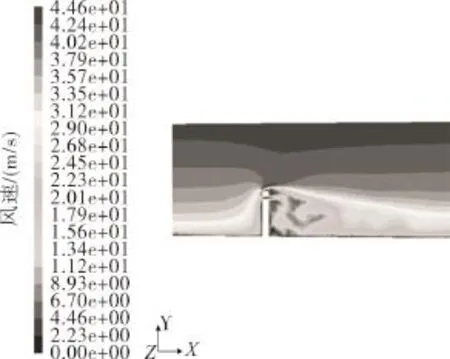
图5 Y=300 m剖面风速分布Fig.5 Distribution of wind velocity atY=300 m profile

由图4，5可以看出：大气层中钝体绕流非常复杂，有冲撞、分离、涡旋、环绕和回流等现象。当气流撞击建筑物的迎风面时发生边界层分离现象，流体的速度在迎风面前方减弱；建筑物的侧面气流分离严重，发生涡旋分离后分离的气流与前方的气流汇合就使得在建筑物两侧风速很大并且形成对称的涡旋；建筑物下游的流场高度涡旋和紊乱，在建筑物的后部形成尾流。气流通过建筑物的洞口时出现明显的狭缝效应，产生局部加速作用。

在洞口的中心线沿X方向布置11个监测点(间距3 m)，沿Y方向布置11个监测点(间距1 m)，洞口内的风速分布见图6。从图6(a)可以看出：洞口中心沿X方向，风速靠近迎风面稍小，当气流在洞口内部时风速很大且在长度方向的中心位置风速达到最大值，为44.11 m/s。如图6(b)所示，洞口中心沿Y方向靠近洞口内壁面的风速较小，远离壁面在洞口的中心则风速较大。洞口内的风速比建筑物顶部远处来流平均风速大很多所以在高层建筑风环境设计中应予以考虑。

图6 洞口内的风速分布Fig.6 Distribution of wind speed in the caves

2.3 风压分布

为了进一步分析建筑物表面的风压分布情况，在建筑物的迎风面、侧面、背风面和洞口布置测点。建筑模型比较规则，所以只分析一个侧面。风压系数[13]

式中：Cpi为平均风压力系数；pi为建筑表面测点的压力；ph为参考高度的静压，取远前方建筑物顶面静压；ρ为空气密度；vh为参考高度处的平均风速。根据式(2)选取坐标点(0，300，180)高度处为参考点，在RNGkε湍流模型中参考点静压值为46 Pa，参考点的风速为37.57 m/s。各测点风压系数分布见图7～10。

由图7可知，在流体作用下建筑物的迎风面均出现正压，迎风面的底部风压小，风压系数在0.5以下；上部风压大最大值出现在洞口上部的中轴线上，最大风压系数达到0.81。由图8可见，建筑物的侧面风压都为负值，风压分布较复杂。最大负压出现在接近迎风面的区域，同时也是整个建筑的最大负压区域，建筑设计时应给予考虑。由图9可见，建筑物背风面风压也为负值，风压分布较均匀风压梯度变化不大。其中背风面的风压分布呈两端大中间小的趋势。结合图7～10可知，洞口的存在使迎风面的正压力值有不同程度的降低且洞口附近风压值降幅最大，洞口附近风压梯度变化也大，洞口对距离较洞口远的区域风压值影响不大。侧面风压系数沿高度方向逐渐增加和洞口等高位置的风压系数增加明显。背风面在洞口附近的风压有所提升，最大风压出现在洞口的两个侧面。

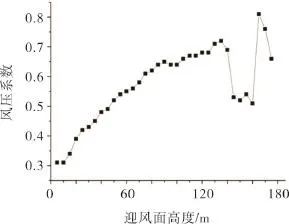
图7 迎风面测点风压系数Fig.7 Coefficients of wind pressure on the windward side points

图8 侧风面测点风压系数Fig.8 Coefficients of wind pressure on the lateral side points

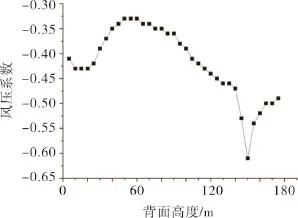
图9 背风面测点风压系数Fig.9 Coefficients of wind pressure on the leeward side points

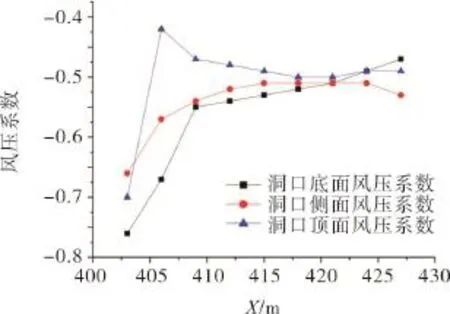
图10 洞口壁面测点风压系数Fig.10 Coefficients of wind pressure on the wall of the caves points

3 不同开洞位置风压分析

为分析洞口在不同位置时风压系数的变化，共设置7个计算工况，见表1。洞口对建筑物的迎风面和侧面影响较大，所以仅研究迎风面和侧面风压系数和顺风向的基底弯矩。

由图11可知在迎风面底部风压系数小，上部风压系数大，各洞口附近的风压系数有所降低，且降幅较大值在洞口0.65h处。远离洞口的区域，开洞建筑和不开洞建筑风压系数基本相同。由图12可见各工况下侧面风压都为负值且风压系数变化较大，其中洞口在0.85h处的侧面风压系数变化较大。当洞口位置比较低时底部风压系数比洞口位置较高时底部风压系数大，且洞口越低底部风压系数就越大。开洞减小了整体侧面风压值，当洞口在0.65h时侧面风压系数平均值比其他工况小，所以当洞口在0.65h时侧面风压系数相对较小。

表1 不同洞口位置工况Tab.1 Working condition of different hole positions

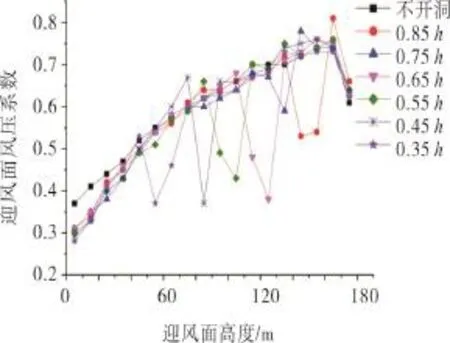
图11 各工况下迎风面测点风压系数Fig.11 Wind pressure coefficients of the measuring points on the wind surface under different working conditions

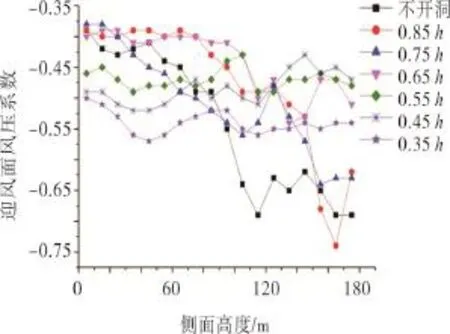
图12 各工况下侧面测点风压系数Fig.12 Wind pressure coefficients of the side measuring points under different working conditions

基底弯矩[14]是衡量风力对整个建筑物作用的一个指标，顺风向的基底弯矩对建筑的影响比较大，所以文中只探讨开洞位置与顺风向的基底弯矩间的关系。对顺风向基底弯矩进行无量纲化处理，可得到相应的力矩系数。各工况下的顺风向基底弯矩系数见表2。

表2 各工况下的顺风向基底弯矩系数Tab.2 Moment coefficients of base bending in the wind direction under different working conditions

由表2可以看出：不开洞工况下顺风向基底弯矩系数最大，其值为0.545；不同的开洞位置都降低了顺风向基底弯矩，其中洞口开在0.65h时顺风向基底弯矩降幅最大；在建筑物的高度上，高度越高风速就越大，并非开洞位置越高就越有利，从本节的分析可知，中上部开洞相对有利，最有利的位置在0.65h处。

4 结 论

选用结构对称的建筑物为研究对象，按照建筑物所处的实际风环境进行设置，得出如下结论。

1)洞口开在0.85h时，风速在迎风面减弱，在侧面风速较大，气流形成对称涡旋。洞口内出现狭缝效应，风速比建筑物其他部位的风速大很多，最大风速可达到44.11 m/s，在设计时要予以考虑。

2)建筑物的下游流场比较紊乱，在背后形成尾流，洞口流出的风在下游形成增大区。在迎风面风压均为正值，在洞口附近的风压会有所降低。侧面风压分布不均匀，都为负值，最大负压出现在接近迎风面的区域。背风面风压都为负值且分布均匀，背面最大负压出现在洞口附近。洞口内主要承受吸力，洞口底部的负压比其他位置负压大，洞口减小了整体的风压值。

3)洞口在不同位置时，对于迎风面洞口附近的风压系数有所降低，洞口在0.65h时降幅较大，其他区域风压系数和不开洞建筑基本相同。侧面风压系数在各工况下变化比较大，洞口等高位置的侧面负压系数有所提高。在0.65h时侧面风压系数较小，同时顺风向基底弯矩也较小，所以在0.65h开洞最为有利。

[1]DAVENPORTAG.Gust loading factors[J].Journal of the Structural Division,1967,93(3):11-34.

[2]WADA A.AIJ recommendations for loads on buildings[S].Tokyo:Architectural Institute of Japan,2004.

[3]CEN T.Eurocode1:Actions on Structures-Part 1-4:GeneralActions-WindActions[S].Brussels:CEN,2004.

[4]ASCE/SEI7-05 Minimum Design Loads for Buildings and Other Structures[S].New York:American Society of Civil Engineers, 2006.

[5]建筑结构荷载规范：GB50009—2012[S].北京：中国建筑工业出版社，2012.

[6]KWOK K C S,WILHELM P A,WILKIE B G.Effect of edge configuration on wind-induced response of tall buildings[J]. Engineering Structures,1988,10(2):135-140.

[7]KIKITSU H,OKADAH.Open passage design of tall buildings for reducing aerodynamics response[C]//Wind Engineering into the 21st Century.[S.L.]:Larose and Livesey Press,1999:667-672.

[8]张耀春，秦云，王春刚.洞口设置对高层建筑静力风荷载的影响研究[J].建筑结构学报，2004,25(4):112-117.

[9]王春刚，张耀春，秦云.巨型高层开洞建筑刚性模型风洞试验研究[J].哈尔滨工业大学学报，2004,36(11):1431-1434.

[10]李秋胜，李永贵，陈伏彬，等.超高层建筑的风荷载及风能发电应用研究[J].土木工程学报，2011,44(7):29-36.

[11]李秋胜，陈伏彬，黄生洪，等.超高层建筑上实施风力发电可行性研究[J].土木工程学报，2012,45(9):11-18.

[12]TU J Y,YEOH G H,LIU C Q.计算流体力学[M].沈阳：东北大学出版社，2014.

[13]苏国，陈水福.复杂体型高层建筑表面风压及周围风环境的数值模拟[J].工程力学，2006,23(8):144-149.

[14]李永贵.高层建筑风荷载与风致弯扭耦合响应研究[D].长沙：湖南大学，2012.

责任编辑：丁吉海

Numerical Simulation of the Influence of Different Opening Height on Wind Characteristics of High-rise Building

XIAXiangzhong，CHEN Ruilin，REN Hailong，HU Di，DENG Xiaobo，ZHANG Chao
(College of Civil Engineering and Mechanics,Xiangtan University,Xiangtan 411105,China)

The numerical simulation is applied to the high-rise building setting hole at the different height in class B landform wind field with RNGk-ε turbulence model and wind speed and turbulence intensity parameter are set by UDF programming.The results indicates when the caves are located in the 0.85h,the wind speed weakens in front of the windward side but enhances on the side so that symmetric vorticities are formed on the side,and the wake flow is formed on leeside;In this condition,slit effect is generated inside the cave and the wind speed reaches the top;The different position of the cave has an impact on the wind pressure of the windward and the side,as well as on the base moment of the windward and the side;Since the side wind pressure coefficient is smaller and the largest decline of the base moment drops when the cave is set at 0.65h,it is the most favorable to set the cave at 0.65h.

k-ε turbulence model；high-rise building with openings；wind pressure characteristics；computational fluid dynamics；numerical simulation

TU973

A

10.3969/j.issn.1671-7872.2016.04.009

1671-7872(2016)04-0354-06

2016-09-21

教育部高等学校博士学科点专项科研基金项目(20104301120004)；教育部科学技术重点项目(211127)；湖南省教育厅优秀青年项目(10B105)；第49批中国博士后科学研究基金项目(20110491260)

夏祥忠(1991-)，男，湖南邵阳人，研究生，主要研究方向为道路与桥梁工程。

陈锐林(1971-)，男，湖南湘潭人，博士后，副教授，主要研究方向为道路与桥梁工程。