对CANDU燃料组件结构的一维瞬态辐射程序开发与验证

高新力，王昆鹏，赵传奇，苏光辉

(1. 西安交通大学能源与动力工程学院，陕西西安710049； 2.环境保护部核与辐射安全中心，北京100082)

对CANDU燃料组件结构的一维瞬态辐射程序开发与验证

高新力1,2，王昆鹏2，赵传奇2，苏光辉1

(1. 西安交通大学能源与动力工程学院，陕西西安710049； 2.环境保护部核与辐射安全中心，北京100082)

在气冷CANDU式燃料组件之中，辐射换热也是不容忽视的一部分。特别是在出现了系统失压/失流事故时，辐射换热将会成为保证燃料安全的主要冷却手段。本文中针对CANDU式压力管编制了针对压力管几何条件下的一维辐射换热瞬态程序。程序中采用将燃料元件棒转化为同心圆环的方式简化辐射角的计算，并加入了隔层辐射模型，使模型更加贴近实际。采用分别将程序中的几个模块的计算结果与CFX计算结果对比的方式来达到程序验证的目的，验证结果显示程序RHTPB具有良好的表现，能够满足于反应堆安全计算的需要。

CANDU组件；辐射换热；瞬态程序

德州大学奥斯汀分校所开发的压力管式聚变裂变混合堆概念[1]，为了能够有效地减小冷却剂的电磁效应和中子慢化效应，并减少腐蚀，采用了氦气冷却方案。同时，为了减小中子需要穿透的结构壁的厚度并较好地承受住冷却剂的压力，概念中采用了CANDU式的压力管式组件设计。

对于气体冷却反应堆的非能动冷却系统设计来说，现阶段主要采用的是依靠气体自然循环能力带走余热或者采用热传导将余热排出的方案。然而对于压力管式聚变裂变混合堆的氦气系统，两种方案都存在一些困难。首先依靠气体自然循环能力来带走反应堆余热的设计需要保证堆芯的压降足够小，这就需要较高的堆芯冷却剂体积比[2]。同时，因为气体的自然循环能力较小，为了保证燃料温度低于限值，就需要提高冷却剂设计压力，这就会造成反应堆工程造价的提高。而对于依靠热传导和热辐射来将余热带出反应堆的系统，需要反应堆内材料具有较大的导热系数，且拥有较大的堆芯内的燃料占空比。而对于压力管式氦气冷却混合堆来说，由于处在聚变堆之中，结构受到很大的限制，而氦气的自然循环能力很差，因此，德州大学奥斯汀分校的设计概念采用了一种新式的余热排出系统设计方案，使用热管作为介质，依靠辐射换热将压力管内的余热排出。

在此类余热排出系统中，热管参数、压力管参数和辐射换热量等关键因素都会影响到系统的正常工作。因此，在系统设计过程中，有必要进行CANDU式燃料组件内的辐射换热计算。现阶段，计算程序CHAN-II[3]以及CATHENA[4]已经能够用于预测表面辐射在热辐射中作为主要辐射方式时的情况。同时，CFX、Fluent等有限元分析程序也被证明能够用于计算CANDU式的燃料棒几何内的辐射换热工况。但是，这些程序应用起来较为复杂，特别是有限元商业程序计算瞬态工况耗时很长。针对上述问题，为了满足设计开发的需求，本文开发了一种新的计算程序RHTPB，能够快速进行CANDU式压力管内的辐射换热计算。

1 瞬态辐射程序的开发

1.1 基本假设

在压力管内辐射换热计算过程中，为了简化计算，我们做了一些基本假设：

(1) 参与辐射的物体表面(包括压力管内壁、燃料包壳外壁)都是漫射(漫发射、漫反射)灰体；

(2) 不考虑压力管或者燃料元件上的轴向温度传递；

(3) 同一根燃料组件内燃料的功率相同。

1.2 数学模型

由于氦气为分子结构对称的双原子气体[4]，在工业上常见的温度范围内，实际上没有发射和吸收辐射能的能力，可以认为是热辐射的透明介质。另外，由于程序计算的对象是氦气冷却压力管式燃料元件发生失流的情况，在此过程中，气体不存在对流换热，加上氦气导热能力并不是热传递的主要因素。因此，从系统设计角度来说，为了获得保守的结果，在计算过程中，不考虑氦气对辐射的吸收以及气体的导热和对流，只考虑燃料元件内部的导热及燃料元件表面间的辐射换热。

因此，燃料芯块的瞬态热传导方程为：

(1)

对于燃料包壳的瞬态热传导方程为：

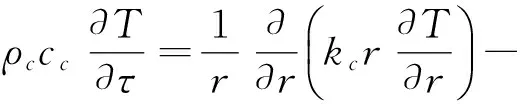
(2)

边界条件为：

其中，ρu为燃料芯块的密度；ρc为燃料包壳的密度；cu，Qv为燃料芯块体积释热率；R代表着包壳的辐射换热。因此，如何确定燃料元件间辐射换热量就成了求解燃料元件温度的关键问题。

在复杂系统中，辐射角的计算一直是辐射热量计算的关键问题。对于CANDU式的棒束来说，本身有着中心对称和圆周均匀的几何，且在模型中，同一燃料组件内功率近乎相等，因此，燃料棒束的同一环上的燃料元件温度分布基本相同。基于以上原因，本文采用了一种合理的简化方式对燃料组件内的辐射换热进行计算。如图1中所示，程序中假设燃料组件里的燃料棒能够被近似转化成为几个同心的圆环，辐射换热只在相邻的燃料环表面进行传递。同时假设燃料元件棒束的轴向无限长。这种假设能够大大降低CANDU式棒束几何的辐射角计算难度，但同时这种假设的缺点在于每个燃料元件上表面的周向不同位置的温度区别不能很好地体现出来。

图1 辐射模型转变方法Fig.1 Radiation Model Transforming Method

模型转换的过程中，确定每一环的内外半径时，需要保证转换后模型中每一环燃料元件的内外表面积分别等于实际模型中每一环上燃料元件的对内总辐射面积和对外总辐射面积。而对内辐射面积和对外辐射面积由具体的棒束几何所确定。同时，为了保证每一圈燃料环拥有与之相应的燃料元件相同的功率，模型转换过程中还根据转换前/转换后的面积比调整了功率密度。例如在图1中，原模型中环2上有6根燃料元件棒，经过转换后，变成了右侧模型中的环2，其中环2的内表面面积与棒束模型中第二圈中所有的燃料棒的能够向内辐射热量的表面积相同，外表面积与棒束模型中第二圈中所有的燃料棒的能够向外辐射热量的表面积相同。

然而，显而易见的是这种逐层辐射的模型与实际情况中的辐射热量传递方式有着较大差异。在棒束模型之中，燃料元件不仅仅与相邻环上的燃料元件进行辐射换热，并且与隔层的燃料棒进行了辐射换热。为了保证模型尽可能的贴近真实情况，假设模型中不仅存在相邻层之间的辐射能量传递，同时也有隔层辐射之间的能量传递。如图1中，从环1表面中发出的辐射能量不仅仅被环2的内表面接收，同时还被环3的一部分内表面所接收。这样的话，计算所用的2面封闭辐射系统变成了图2中所示的3个面所组成的封闭辐射系统。其中，表面1到表面4的辐射角等于图1中环3上空隙所占的比例。

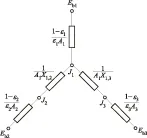
图2 辐射电阻模型Fig.2 Radiation Resistance Model

2 瞬态程序的验证

因为缺乏实验数据，程序中的辐射模型、瞬态辐射计算模块以及稳态辐射计算模块分别由CFX进行了校核。

2.1 稳态结果校核

本文使用RHTPB程序和CFX对同一稳态算例进行计算，并通过与算术解进行对比来验证程序中稳态辐射计算的正确性。

稳态算例是对几个同心圆环中的辐射换热量进行计算。如图3中所示，最内环的固态辐射盘的半径为R1,out，其余各个同心圆环的内外半径由内至外依次为R2,in,R2,out,R3,in,…R5,in。所有表面的发射率假设为0.8。假设环间气体为氦气。氦气作为双原子对称结构，可以视作辐射透明介质，因此燃料环表面之间的热传递仅仅通过热辐射进行。两个相邻的表面间，比如环2的外表面与环3的内表面，组成一个完整的封闭辐射系统。假设燃料元件和压力管的材料导热率都足够大，使每个环内部的温度差小到足以忽略。每一个燃料环内的功率密度均为0.8MW/m3，并假设压力管的外表面的温度为573K恒温。

图3 稳态验证算例Fig.3 Steady State Verification Example

使用CFX进行计算时，假设材料的导热率为5000 W/(m2·K)，使每个环内部的温度差小到足够忽略。模型两端设置为对称边界条件，以保证可以等效为无限长的圆柱体。由于采用He作为气体工质，将气体导热系数设置为0，同时将氦气的辐射吸收系数设置为0，并采用适合计算无气体辐射的Monte Carlo模型来模拟氦气辐射透明的特性。经过对不同网格数量的CFX模型进行了敏感性分析后选择了合适数量的网格，如图4给出了CFX计算的网格。

图4 稳态验证算例网格Fig.4 Mesh of Steady State Verification Example

图5中给出了CFX计算结果的温度分布图。图中可以看出，由于材料的导热率设置的足够大，每一环的温度均一致。温度从内向外逐层降低，最外层的温度为573K，而最内侧的燃料棒温度为887K。

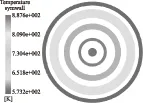
图5 稳态验证算例的CFX计算结果Fig.5 Steady state result of CFX calculation

表1中给出了稳态算例的结果对比，从表中我们可以清晰看出程序RHTPB的计算结果和数值解保持了非常好的一致性，证明程序RHTPB在辐射换热量计算上的合理性。同时，CFX计算结果与数值结果相差很小，可以认为CFX用于辐射性计算具有相当的可靠性，且计算中模型设置方法正确，可以作为程序校核的参考。

表1 CFX稳态算例计算结果与RHTPB

2.2 模型校核

为了检测RHTPB程序中将CANDU式燃料组件处理成几个同心圆环来计算辐射换热的方法的正确性，本文将RHTPB计算结果和CFX计算结果进行比较。另外，由于几何结构复杂，辐射角难以计算，难以计算出数值解。因此，我们采用对几何结构不敏感的CFX进行对比计算，来验证RHTPB程序的计算结果。

图6给出了计算对象的截面图。如图中所示，压力管内共有37根燃料元件。按CANDU式燃料组件方式排列，37根燃料元件分别处在4个不同半径的同心圆上。燃料为压水堆式燃料棒，内部为UO2芯块，外部包裹着燃料包壳，包壳与燃料棒间的等效热传导系数为5678 W/(m2·℃)。燃料元件在两端固定，因此内部无其他定位格架影响棒间辐射。燃料元件长度远大于10倍直径，可等同无限长圆柱间传热问题。氦气为双原子对称结构，对于热辐射的吸收能力非常小，可视作辐射透明介质。

图6 模型转化方法验证算例Fig.6 Modeling Method Verification Example

CFX计算中，选择Monte Carlo辐射模型模拟压力管内的气体透明辐射特性。燃料棒的功率密度为0.8MW/m3，压力管的外表面的温度为573.1K恒温，燃料棒的初始温度设置为625K。包壳与燃料棒间的等效热传导系数为5678 W/(m2·℃)。压力管两端为对称边界，从而能够消除压力管长度对辐射角的影响。所有辐射表面的发射率假设为0.8。

图7给出了CFX计算的计算网格。网格采用六面体网格划分，质量达到0.5以上，并经过网格数量敏感性测试，保证了计算结果的网格无关性。图8给出了压力管辐射问题的CFX计算结果。可以看出，由于燃料元件内部的功率较低，燃料元件内的功率分布较为均匀。燃料元件的温度由内至外依次降低，且由于几何结构的中心对称性，同一环上的压力管温度相同。

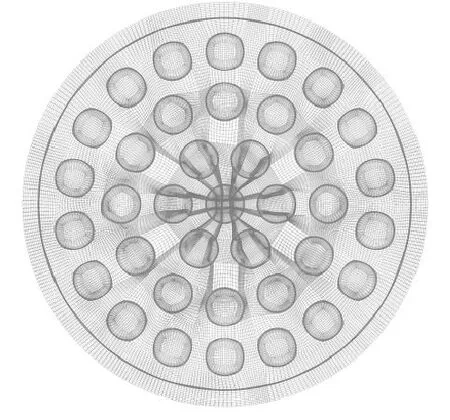
图7 模型转化方法验证算例的计算网格Fig.7 Mesh for Modeling Method Verification Example

图8 模型转化方法验证算例的CFX计算结果Fig.8 CFX Result for Modeling Method Verification Example

在RHTPB程序的计算过程中，会将图7中的燃料组件模型转化为图9中所示的同心圆环燃料形式，图9中还给出了转换后模型的具体尺寸。其尺寸确定原则为：每一环的内/外表面积分别等于图7中燃料组件模型上相应环上的燃料棒的向内/外辐射面积。例如图9中的表面7，其表面积等于压力组件中第4环上18根燃料组件的能够直接与压力管进行辐射换热的表面积之和。但这也导致每一环的燃料环体积与燃料组件内相应的燃料棒体积不同，程序内通过改变燃料环内的功率密度使得转化后的模型与原模型拥有相同的总功率。另外，燃料环厚度的变化，也会影响到燃料元件内部导热的计算，因此在燃料棒内导热计算过程中，燃料环的厚度不作为导热计算的输入，而是使用燃料棒的直径作为燃料环导热的传输距离，使设计结果更为保守。

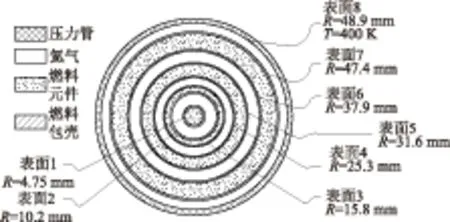
图9 程序RHTPB模型转化结果Fig.9 Modeling Transfer Result of RHTPB

可以看到在实际的燃料组件模型中，燃料元件不仅仅和相邻环上的燃料元件进行换热，同时还会穿过燃料元件之间的缝隙与间隔层进行辐射换热。因此，为了使转化后的模型更加接近真实模型，我们假设在转化后的模型中，辐射不仅仅存在于两个相邻的表面间，也存在于相隔的燃料元件环之间。比如辐射换热不仅仅存在于表面1与表面2之间，在表面1与表面4之间也存在辐射换热。

图10给出了CFX与程序RHTPB的计算结果对比。为了体现出间隔辐射模型对计算结果的影响，程序RHTPB分别对采用间隔辐射模型和不采用间隔辐射模型的情况进行了计算。图中可以看出，不采用间隔辐射模型时，程序RHTPB计算出的每层燃料环的最高温度远远高于CFX计算出的每环燃料的最高温度。而采用间隔辐射模型时，程序RHTPB计算结果与CFX计算结果相对符合较好，且程序计算结果温度比CFX的计算结果高，满足设计中保守计算的需求。另外，不考虑间隔层燃料环之间的辐射时，每层燃料环之间的温差也更大。而在考虑了间隔辐射之后，每层燃料环之间的温度变化也相对平缓，更贴近CFX计算出的结果，说明间隔辐射模型更符合实际情况。

图10 间隔辐射模型计算结果对比Fig.10 Comparison of Result calculated with and without gap radiation model

2.3 瞬态工况验证

为了验证程序的瞬态计算模块是否正确，本文使用RHTPB和CFX对同一瞬态算例进行计算，并将结果进行比较。

如图11所示，瞬态工况包含从一个自发热的内管向外侧的薄管辐射换热的瞬态过程，假设里侧的发热盘和外侧的薄管的热导率非常大从而能够保证其内部的温差小到可以忽略。辐射表面发射率均为0.7，表面2恒定温度873.15K。假设表面1和表面2之间只有辐射换热。在T0时刻，内管突然停止发热，计算之后内管温度的变化情况。

图11 瞬态工况验证算例Fig.11 Transient State Verification Example

图12中给出了CFX和程序RHTPB计算结果比较。图中黑点为H.T.KIM用CFX计算的结果[6]。代表程序RHTPB计算所得到的结果。可以看出，内部的管壁温度T1从初始温度1673.15K开始下降，直至最终降至与外侧温度T2相同。由于辐射换热量随着温差减小而减小，温度下降的速率也越来越慢。程序与CFX计算结果符合非常好，证明了程序瞬态计算模块的可靠性。

图12 瞬态工况验证结果Fig.12 Comparison of CFX and RHTPB Result for Transient State Verification Example

3 总结

本文提出了一种计算CANDU式燃料组件内辐射热量计算的简化方法，并编制了程序RHTPB。通过加入间隔辐射模型，减小了环形燃料辐射模型与实际辐射模型的计算结果的差距。本文通过分别校核程序中的辐射模型、

瞬态辐射计算模块以及稳态辐射计算模块来达到验证校核程序的目的。与CFX结果的比较证明了程序计算结果的可靠性，证明了本程序可以应用于氦气冷却的CANDU压力管式反应堆失流事故后燃料棒温度计算。

后续工作将围绕加入非辐射透明气体模型展开，研究非辐射透明气体介质对辐射换热的影响。

[1] M Kotschenreuther, P M Valanju, S M Mahajan, E A Schneider. Fusion-Fission Transmutation Scheme—Efficient destruction of nuclear waste[J]. Fusion Engineering and Design， 2009，84(1) ：83-88.

[2] M A Pope，J I Lee, P Hejzlar, M J Driscoll. Thermal hydraulic challenges of Gas Cooled Fast Reactors with passive safety features[J] . Nuclear Engineering and Design，2009，239(6)：840-854.

[3] D Bowslaugh. CHAN-IIA MOD 2.0: Prediction of CANDU Fuel Channel Behaviour Under Prolonged Low Flows—Program Description[J]. Atomic Energy of Canada Limited，1993, vol.TTR-490.

[4] B N Hanna. CATHENA: A thermal hydraulic code for CANDU analysis[J].Nuclear Engineering and Design，1998，180(2)：113-131.

[5] 杨世铭,陶文铨.传热学[M].北京:高等教育出版社，2006：419-420.

[6] H T Kim, B W Rhee, J H Park. “Benchmark calculations of a radiation heat transfer for a CANDU fuel channel analysis using the CFD code[J]. Journal of Nuclear Science and Technology，2006，43(11)：1422-1430.

Development and Verification of a One Dimensional Transient Radiation Code for CANDU Fuel Assembly

GAO Xin-li1，2，WANG Kun-peng2，ZHAO Chuan-qi2，SU Guang-hui1

(1. School of Energy and Power Engineering, Xi’an Jiaotong University, Xi’an 710049, China; 2.Nuclear and Radiation Safety Center, Ministry of Environmental Protection, Beijing 100082, China)

In the Gas-cooled CANDU kind fuel assemble, radiation heat transfer cannot be ignore. Expertly during the LOFA accidents, with no convection heat transfer, the radiation heat transfer will become the main force to ensure the safety of the reactor. This paper developed a one dimensional transient radiation code to calculate the radiation heat transfer in CANDU fuel assembly. The code assumes that the fuel element rings can be lumped into several circular rings, which can simplify the calculation of radiation angle factors. And with the purpose of making the models closer to the actual situation, radiation between next nearest neighbor layers is also considered in addition to that between nearest neighbor layers. The radiation model, transient radiation calculation and steady radiation calculation of the code RHTPB are verified by comparing with result of CFX, respectively. The result shows that the code has good performance in transient radiation calculation, and can satisfies the need of nuclear industry.Key words: CANDU Bundles; Radiation Heat Transfer; Transient Code

2016-02-11

高新力(1988—)，男，陕西省，工程师，博士，核科学与技术专业，现从事核安全科研方向工作

TL333

A

0258-0918(2016)06-0739-07