白糖期货最优套期保值比率实证研究
□文/汪 娟
(安徽财经大学金融学院 安徽·蚌埠)
“民以食为天”,农产品价格是否稳定关系着国家安全、社会秩序乃至国计民生。白糖是在农产品中仅次于粮食、油料和棉花,交易量居第四位的大宗商品。白糖的现货市场价格受甘蔗产量、气候、季节因素、国家宏观调控、产销关系、替代品、节假日以及国际市场价格等因素影响。这些因素都会使国内的白糖现货市场价格波动频繁且剧烈,这样会严重影响白糖行业的稳健发展。企业可以用期货市场来规避价格波动的风险,建立多种投资策略,在一定程度上规避风险。本文研究的意义是想通过对期货的介绍,让投资者选择更好的套期保值策略来提高资源利用率,锁定风险、提高企业的市场竞争力。
一、相关文献综述
张月萍(2013)利用收集到的白糖数据,运用OLS模型进行最优套期比率的分析,在“风险最小化”的基础上,运用“效益最大化”原则进行比较,发现期货的一些特有的基差风险,会降低期货套期保值的效果,但加入期权后会使套期保值得到改善。梁权熙、欧阳宗旨(2008)以白糖期货为例,采用不同的模型估算套期保值比率,并选取样本内数据和样本外数据对套期保值的有效性进行分析,得到期货市场的套期保值能够降低现货市场价格波动以及组合资产收益风险,并且得到在采用的众多模型中利用ECM模型估计得出的套期保值比率进行套期保值效果最理想。韦景忠(2007)在期货市场发展背景下总结出白糖期货有稳定价格、增加农民收入以及企业竞争力的作用,并能够有效解决白糖生产的季节性问题。进行简单的利用最小方差套期保值法在有交易成本和无交易成本情况下的套期保值率,发现有无交易费用,套期保值比率差别不大。王志刚(2015)运用PP检验、Johanson检验以及格兰杰因果检验证明我国白糖期货市场是有效的,信息在期货市场和现货市场之间是双向传导;与现货市场相比,期货市场在非均衡的情况下反应速度更快、强度更大。
本文研究白糖期货的最优套期保值比率,首先选取样本数据并对样本数据进行平稳性和协整检验,其次灵活运用OLS、B-VAR、ECM等套期保值估计模型计算在各自套期保值模型下的套期保值比率,通过收益方差法对不同套期保值模型的套期保值绩效进行评价,相较之下得出我国白糖期货市场基于ECM模型下的套期保值比率最佳,最后根据套期保值比率提出有效的交易策略。
二、数据的选取和检验
(一)样本数据的选取。本文以白糖为研究对象,样本选取时间范围是2014年9月17日至2015年12月24日,数据经过整理,共得到310个样本观察值。对于白糖期货价格的选取,期货日数据来自Wind资讯。为避免研究过程中发生序列相关,选择期货合约收盘价组成期货价格的时间序列。白糖现货价格也来自Wind资讯,为市场报价每日的收盘价。
(二)数据的平稳性检验。平稳性检验在时间序列分析中是一个十分重要的环节,如果选取的时间序列是非平稳的,对其进行回归分析就是伪回归,只有选取时间序列是平稳的,对其进行回归分析进而推测未来特征才有意义。本文的平稳性检验采用ADF检验方法,分别对白糖现货价格序列St,期货价格序列Ft,现货价格的一阶差分序列△S,期货价格的一阶差分序列△F进行平稳性检验,结果如表1所示。(表1)
由检验结果表明,在1%、5%、10%的置信度水平下,由于白糖现货价格序列St、期货价格序列Ft的ADF统计量均大于临界值,即St和Ft均为非平稳的时间序列。但一阶差分后的白糖现货价格△S和一阶差分后的期货价格△F的ADF统计量值均小于1%、5%和10%临界值,说明一阶差分后的△S、△F均是平稳的时间序列。因此,可以选取现货价格的一阶差分序列和期货的一阶差分序列进行回归分析。
(三)协整关系检验。由之前ADF检验已经知道白糖现货价格时间序列St和期货价格时间序列Ft都是非平稳性时间序列,经过进一步检验,发现两者都是一阶单整序列。由于两个变量同阶单整符合协整的基本条件:首先以白糖现货价格时间序列St为被解释变量,以期货价格时间序列Ft为解释变量进行OLS回归;然后对回归方程得到的残差序列进行单位根检验和平稳性检验,结果如表2所示。(表2)
由表2可知,残差序列ADF统计量值为-3.059919,均小于置信度为1%、5%和10%的临界值,拒绝残差序列存在单位根的假设,即回归方程的残差序列为平稳序列。结果说明白糖现货价格和期货价格存在长期均衡关系,白糖的期货价格序列和现货价格序列存在协整关系。
三、最优套期保值比率计算
(一)简单回归模型(OLS)。OLS模型是利用最小二乘法计算最优套期保值比率,是目前比较常用的一种方法。模型形式如下:

其中,△St、△Ft分别表示现货市场价格的一阶差分和期货市场价格的一阶差分,回归方程的斜率h1为估算的最优套期保值比率;α为截距项,在回归时常常被忽略;εt为随机误差项。利用Eviews软件对△St、△Ft进行回归分析,得到的回归方程为:

从回归方程看,通过该模型估算出白糖最优套期保值比率为0.513335,也就是说,要用0.513335单位相反的期货头寸才能对冲1单位的现货头寸,才能最大限度地降低白糖现货市场的价格风险。
(二)贝叶斯向量自回归模型(B-VAR)。简单回归模型忽略了历史信息产生的自相关问题,导致对期货价格与现货价格两者之间可能存在滞后期,而且随机误差项之间存在着自相关。针对这些问题提出了B-VAR套期保值模型,在B-VAR模型中,建立如下现货价格与期货价格之间的关系式:

其中,Cs、Cf为各自回归方程的截距,εst、εft为各自回归方程的随机误差项,αsi、αfi、βsi、βfi为各自回归方程的系数。在该模型中可以通过AIC准则和SC准则找到两个变量的滞后阶数,进而消除自相关。令Var(εst)=σss,Var(εft)=σff,Cov(εst,εft)=σsf,可以得到最优套期保值比率:
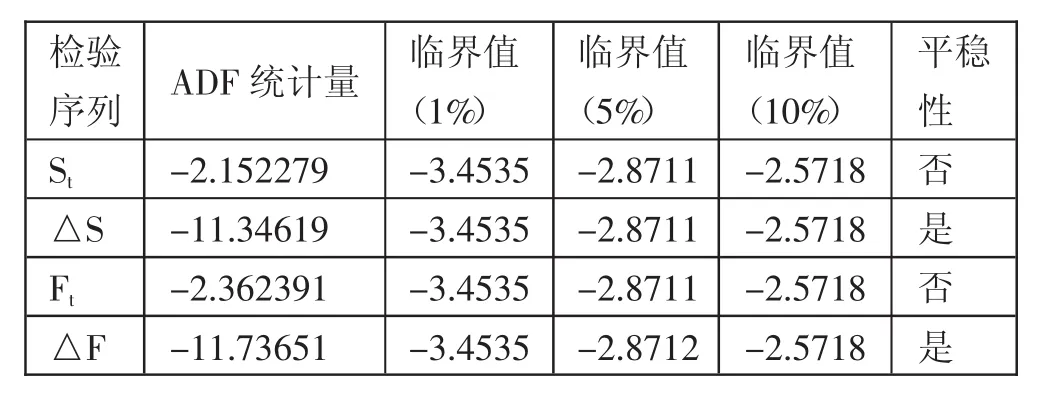
表1 白糖现货价格与期货价格的ADF检验

表2 残差协整检验

表3 各模型套期保值绩效比较

△Ft的回归系数h2即为估算的最优套期保值比率,最优套期保值比率h2与上面的最优套期保值比率h相同。将两变量的历史变动信息考虑到模型中,并根据准则建立多种包含现货价格和期货价格滞后期的回归模型,得到现货的价格变动量的滞后阶数为1,期货的价格变动量的滞后阶数为0,回归方程为:
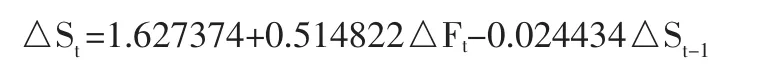
方程的t、F均通过显著性检验,即得到的最优套期保值比率为0.514822,即每单位的现货头寸要用0.514822单位相反的期货头寸对冲,才能有效地降低白糖现货市场的价格风险。
(三)误差修正模型(ECM)。OLS模型和B-VAR模型考虑到了时间序列相关性和残差序列自相关性,但忽略了现货市场价格和期货市场价格之间的长期均衡关系。为解决这个问题,可采取误差修正模型,使用E-G两步法估计最优套期保值比率。
第一步,对St和Ft的平稳性进行检验,如果St和Ft均为平稳序列,则回归方程为:St=a+bFt+εt。如果现货、期货价格序列不平稳,则对方程St=a+bFt+εt的残差项进行平稳性检验,如果残差项是平稳的,则现货和期货价格的序列就是协整的。之后将方程St=a+bFt+εt的残差项作为误差修正模型的修正项。
第二步,利用上一步的误差修正项εt,构建现货价格的一阶差分△St和期货价格的一阶差分△Ft之间的误差修正模型:
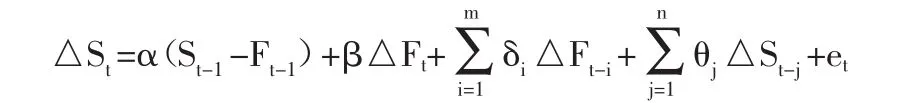
其中,模型中期货价格的一阶差分△Ft的系数β就是最优套期保值比率。
结合数据,得到误差修正模型的回归估计结果为:
F统计量为86.58177,回归方程系数是通过检验的,自变量系数和误差修正项系数在5%的置信水平下是显著的。通过误差修正模型估算出的最优套期保值比率为0.521385,即每单位的现货头寸需要0.521385单位相反的期货头寸对冲。
(四)套期保值绩效的衡量。不同模型的套期保值效果可以用套期保值绩效来衡量,把套期保值后的收益方差与未进行套期保值的收益方差进行对比,套期保值绩效公式表示为:
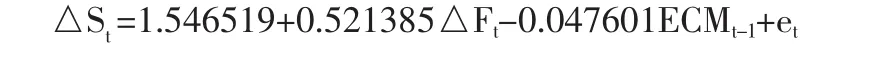

其中,Var(Ut)=Var(△St)表示未进行套期保值收益的方差;Var(Pt)=Var(△St)+h2Var(△Ft)-2hCov(△St,△Ft),表示进行套期保值的收益方差,其中h表示最优套期保值比率;He表示套期保值绩效的指标,He的数值越大,表示套期保值效果越好。计算OLS、B-VAR、ECM模型下的套期保值的绩效,如表3所示。(表3)
由表3可以得到以下结论:第一,通过OLS、B-VAR、ECM模型估算出的白糖期货最优套期保值比率分别为0.51335、0.514822、0.521385,均小于传统市场的套期保值比率1。当投资者投资同等数量的白糖商品时,所需的现货头寸数量是高于期货头寸数量的,即期货市场投资的成本低于其在现货市场上的成本。所以,当利用估算出的最优套期保值比率进行套期保值的操作时会减少支出,降低交易成本;第二,从表中可以得到OLS的套期保值绩效为0.715157,B-VAR的套期保值绩效为0.713505,ECM的套期保值绩效为0.726154。从整体上来看,各模型的套期保值绩效的指标值是比较高的,其中ECM模型的套期保值绩效最好。说明采取套期保值操作后,能够在一定程度上降低投资组合的非系统性风险。
四、结语
本文选择白糖期货的现货与期货每日收盘数据,对数据进行协整检验,发现白糖现货价格和期货价格存在长期均衡关系;利用OLS、B-VAR、ECM套期保值模型进行实证研究分析,得出基于ECM的误差修正模型的套期保值绩效最好。此外,在期货市场上选择最优套期保值比率进行套期保值能有效转移现货价格波动风险,降低交易成本,因此研究白糖期货市场的套期保值比率对经营者和投资者都有重大意义。
[1]张月萍.白糖企业套期保值实证检验[D].河南:河南大学,2013.
[2]梁权熙.我国期货市场套期保值有效性实证研究——以白糖期货为例[J].金融发展研究,2008.11.
[3]韦景忠.浅析白糖期货功能以及套期保值方法[J].学术论坛,2007.2.

