两种周期型遥测数据建模模型及其初始化算法
王永生杜彬彬孙瑾++代进进�┆�


摘要:在对某大型航天电子设备的遥测数据建模预测时,遇到多是不规则周期型数据,对其进行建模预测可以在早期及时发现设备性能异常。针对有周期规律的遥测数据,提出采用Fourier级数模型、sin函数和模型对遥测数据建模,给出了这种数据模型的表达式,研究了基于FFT的两种模型的参数初始化算法。通过数值实验说明模型参数初始化算法的有效性,为后续利用最优化理论求解模型精确参数提供了良好的初试点。
关键词:遥测数据;预测;周期模型;初始参数
中图分类号:P207.2文献标识码:A
1引言
利用大型航天电子设备的历史采集数据,采用适当的预示分析方法,开发对电子设备遥测数据变化进行预示分析的工具,实现对航天电子设备采集数据进行建模,完成拟合及长预示,可以为研究大型电子设备性能的变化规律、分析实际变化与设计值的差异等提供手段。对于大量表现出周期特点的遥测数据,需要给出可行的数据模型,模型要求具有一定适用性,不局限于某一个特定的遥测数据。另外,从工程应用的实际需要考虑,还必须根据遥测的数据能够快速计算出模型的初始参数,也就是要有模型参数的初始化算法[1]。根据一部分遥测数据求出的初始参数,未必是模型参数的精确解,但是可以为后续利用最优化理论的方法,迭代求解更为精确的解模型参数提供较好的初始点,提高迭代收敛速度[2~4],满足工程应用需要。本文着重探讨可行的周期型遥测数据建模模型,结合大量遥测数据给出模型参数初始化算法。
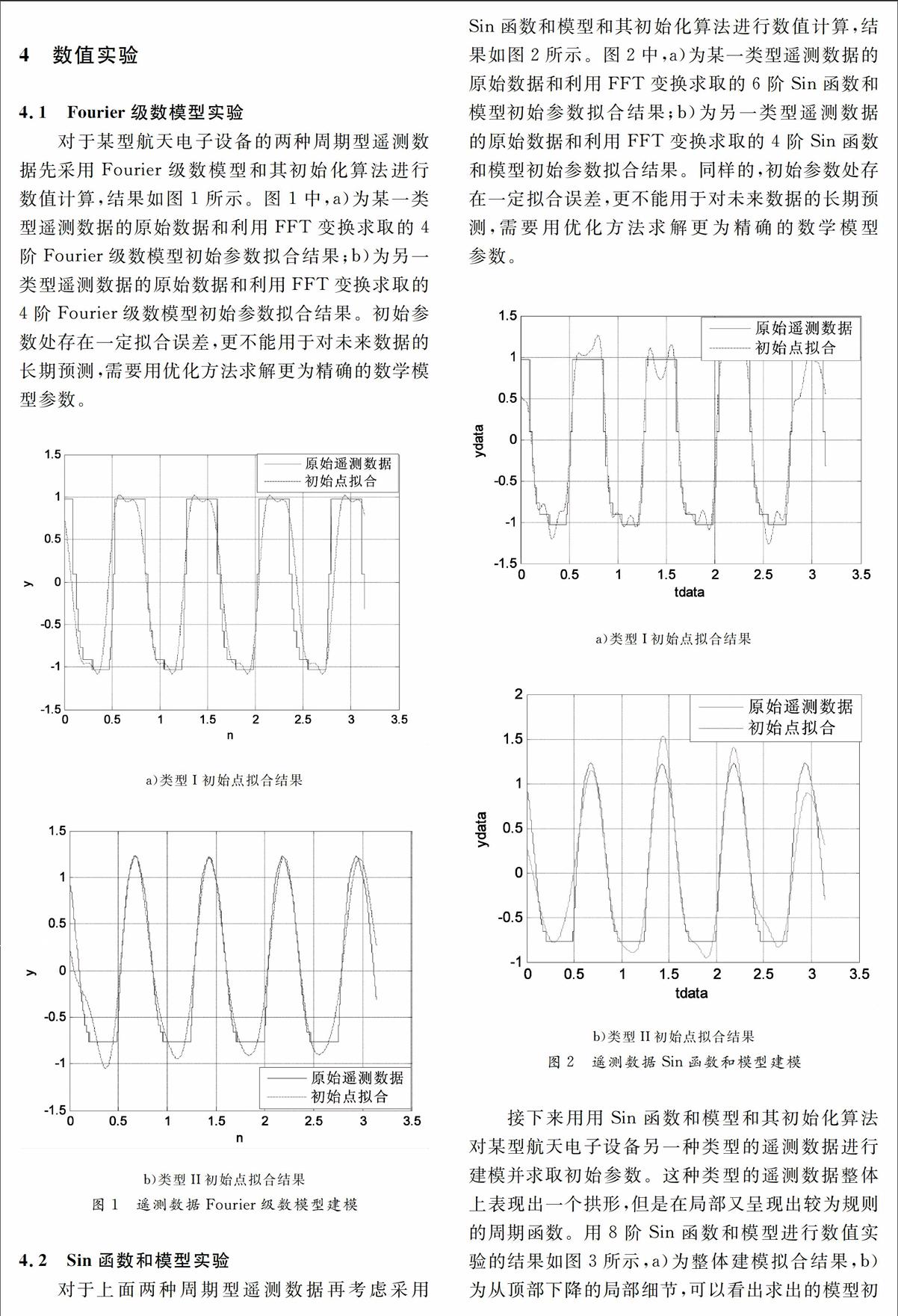
某型航天电子设备某遥测数据中包含一个变化周期的数据量通常需要近万个,为了拟合和预测往往需要有约五个周期的以上的数据,即大约需要40000多个以上的数据。因此,这涉及到大规模数据处理问题,为了工程应用需要采用的数据处理方法必须满足时间复杂度需要,即要求尽可能短的时间完成建模及预测。首先将要处理的遥测数据序列转换为y,t,其中y和t均为m维列向量,m即为所获得的原始遥测数据的个数。为了方便计算,通常要先对数据进行预处理,剔除野值,对采样数据进行去均值并进行必要的尺度压缩,即将数据大小幅值和坐标宽度变换到一定数值范围内,文中假设已完成上述预处理过程。
5结束语
对于周期型遥测数据,给出能够较好实现对周期数据建模的Fourier级数模和Sin函数和模型,基于FFT研究了两种模型的参数初始化算法,并对遥测数据进行了数值实验,实验结果说明模型初始化算法可以提供了良好的初始点,有利于进一步采用优化算法快速求得全局最优点,获得更为精确的模型参数,实现对遥测数据的准确建模。
参考文献
[1]李奎山.超越方程的诺模图求解[J].石油大学学报:自然科学版,1996,20(2):118-119.
[2]PHILIP E,GILL, WALTER MURRAY,MARGARET H.Wright. Practical optimization[M]. London: Academic press,1981,83-153.
[3]刘兴高, 胡云卿. 应用最优化方法及Matlab实现[M]. 北京: 科学出版社, 2014,(1):89-109.
[4]倪勤. 最优化方法与程序设计[M]. 北京:科学出版社, 2009,(6):25-39.
[5]Abuelma'atti, Muhammad Taher. A simple algorithm for fitting measured data to Fourierseries models[J].International Journal of Mathematical Education in Science and Technology,1993,24(1):107-112.
[6]GENE H,GOLUB,CHARLES F.Van Loan. Matrix Computations(3rd Edition)[M].Johns Hopkins University Press, 1996:206-255.
[7]Sum of Sines Models[EB/OL]. http://www. mathworks.cn/cn/help/curvefit/sumofsine.html [2014-2-12].

