基于引力搜索算法的RSSI 模型优化与在消防定位中的应用

杨勇



基于引力搜索算法的RSSI 模型优化与在消防定位中的应用

杨勇

摘 要：RSSI 定位方法成为近年来研究的热点问题。用极大似然估计法得到RSSI 测距模型的修正参数，再使用最小二乘法求取所需节点的估计坐标，再通过引力搜索算法对最小二乘法的初步坐标估计结果和参数进行优化和修正，其算法不仅可以提高定位节点坐标的精度，还可以实现对于定位模型参数的动态跟踪变化。将设计的RSSI定位系统的应用程序移植消防定位系统中，通过接收网关节点从串口传递进来的参考节点的位置信息和参考节点接收到定位节点广播的RSSI 值，通过提出的算法求解出最终的定位节点的位置。最后，在消防定位的实验结果中验证定位模型的参数优化结果，设计的RSSI定位系统总体误差较小，得到的参数反映了环境的变化，取得了预期的效果。

关键词：定位；引力搜索算法；消防；无线网络

0 引言

随着社会的发展，确定位置信息显得越来越重要，一些产品诸如手机、平板电脑、汽车等，早已具备了定位的功能。定位技术在消防中同样可以得到较为广泛的应用，如消防员位置监控、监控消防的特殊地点。基于ZigBee 无线网络的接收的信号强度指示（Received Signal Strength Indication，RSSI）测距法由于其低成本，低功耗，无额外硬件，将其应用于消防定位是一种较为良好的选择。对于定位问题来说，提出一种定位精度高，实时性强，受环境影响小的算法，无疑具有重要的意义。

1 引力搜索算法对RSSI 模型结果的优化

使用无线传感器网络来确定位置信息，都是基于接收信号强度RSSI 值与距离之间的数学模型，求出各节点之间的相对位置，最后使用设定的定位算法求得所需节点的位置。RSSI 定位的方式虽然实现较为简单，但由于无线信号的强度往往受到障碍物吸收、反射的影响，而且容易还会发生多径效应等，因此，在实际的操作过程中传统的RSSI 定位精度通常不高。本文提出将引力搜索算法（gravitational search algorithm，GSA）使用到RSSI 定位方法中。主要实现的过程是：

（1）利用极大似然估计法得到RSSI 测距模型的修正参数；

（2）使用最小二乘法（least square method，LSM）初步估计所求的定位节点的坐标；

（3）使用GSA 对使用LSM 计算出来的定位节点坐标和参数进行优化。此算法能够提高所求取的定位节点坐标的精度，而且实现对定位模型的参数的动态跟踪，提高系统对环境的适应性。

在对RSSI 定位进行研究中，一般使用,定位模型，如公式（1）：

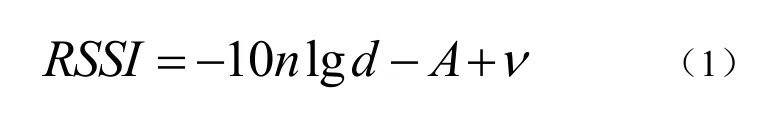
其中，A表示距离1m 处的RSSI值， n为路径的衰减因子，取值通常为1~4之间，ν服从（0，δ2）的高斯分布，用来表示环境对数学模型的影响程度。为了更加此处令a=10n，b=A，这样更加明确的体现数学模型中的线性关系，可以得到公式（2）：

RSSI 定位的方法是基于测距的算法，通常使用三边测距法，其基本原理是当参考节点与定位节点的距离已知时，将定位节点看成是以参考节点为圆心，半径为该距离的圆上的一点，定位节点就是至少3个参考节点的圆相交的交点，由此推断出定位节点的位置。

通过前文的推导，已经将RSSI 定位模型的参数求出，将求解出来的参数代入式（2），就可以通过读取组网后的第i 个节点接收到的RSSI 值求得定位节点和参考节点的相对距离di ，设现已知n 个参考节点与定位节点的相对距离，x i， yi分别代表第i 个节点参考节点的横坐标和纵坐标，x 和y 为需要的定位节点估计坐标。则有：

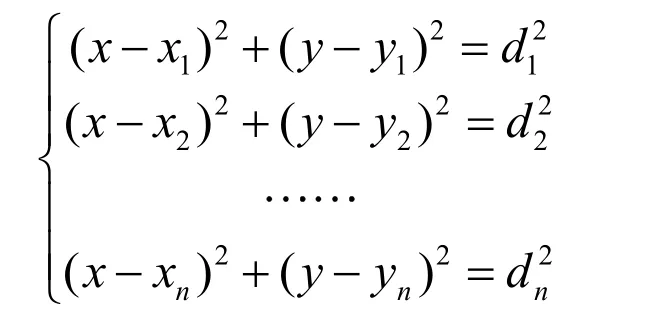
为了应用最小二乘法，需要将上述的二次方程组转换为一次方程组，可以通过将前(n-1)个方程都减去第n个方程的方法实现，得出：

对于上述方程组若分别令：

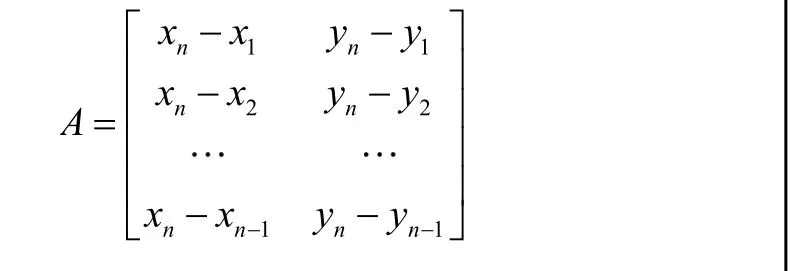
就可以将方程组写为最小二乘法的基本方程的形式：

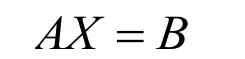
由上文中推导的解方程的结论，得到公式（3）：

这样就可以将定位节点的坐标给估计出来。然而，单纯的使用最小二乘法得到的估计坐标在环境影响不大或者环境条件改变较小时可以得到较好的结果。但实际应用中，环境是不断变化的，所以，使用相应的人工智能算法对求取出来的估计结果进行优化，提升整个系统模型对环境的适应能力，还是很有必要的。

若将上述最小二乘法得到的结果用来缩小人工智能算法的搜索范围，可以为进一步优化坐标提供条件，减小因为智能算法由于搜索范围过大所带来的误差，由于引力搜索算法对局部和全局的搜索性能好，速度较快，这里使用引力搜索算法对刚才估算出来的定位结果进行优化。

引力搜索算法是由伊朗的克曼大学教授Rashedi 等人提出来的优化算法，主要思想是每个粒子都会由于万有引力相互吸引，引力的大小与粒子的质量成正比，与它们之间的距离成反比。本文使用改进的引力搜索算法优化前文中所得到的估计坐标，此处设最终需要的定位节点坐标为(x，y)，通过公式（3）计算出来的估计值为(x'，y')，其中代表一个给定的正数，此处将其称为调节因子，主要用来调节算法的优化范围。此处可以看出，若调节相应的调节因子，可以将x 和y 的取值扩展所有可以取值的区域，这样可以避免使用最小二乘法进行初步估计，单纯的使用引力搜索算法，但是这样做无疑大大增加了计算机的负担，使求解最终结果的效率大为下降。而先使用最小二乘法，再对估计结果进行优化尽可以大地缩小求解的优化范围，求解的效率与精确度都得到了较大幅度的改善。

对于一般的 RSSI定位模型，参数的取值范围为a∈(-40，-10)，b∈(-50，-30)。由于读取出来的RSSI 值在程序中通常是绝对值，故利用RSSI 绝对值得出的a、b一般均为负数。

在上述x 、y 、a 、b 的取值范围的条件下随机产生N个粒子，其中第i个的位置为分别对应于所需要的x 、y 、a 、b 。对于人工智能算法来说，通常选取的粒子数越多所得到的结果就越精确，当然运算量也就越大。选用作为该粒子在第d 维上的位置大小。在t 时刻（也就是第t次的迭代），第d 维上第i 个粒子所受到的总的作用力的大小可看成是其他适应度最大的粒子对其作用力的和，如公式（4）：

上式中kbest表示选出的适应度最大的粒子的集合。randj是[0，1]间的随机数，表示的是第j个粒子对第i个粒子在t 时刻的作用力，通过公式（4）就可以求得公式（5）：

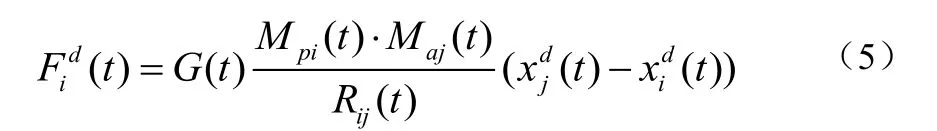
式中，Mpi（t）、Maj（t）分别代表第i个粒子和第 j个粒子于 t 时刻的惯性质量，R ij（t）表示在此时刻的两个粒子之间欧氏距离，是一个很小的常量，通常在程序中直接选定一个较小的数，G（t）所表示的是当前时刻的引力常数。使用公（5）得到公式（6）：

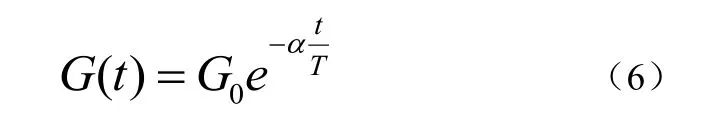
通常G0直接取100，而α 直接取20，T 表示的是系统的最大迭代次数。

确定了作用力之后，再依据牛顿第二定律来求解此时的加速度如公式（7）：

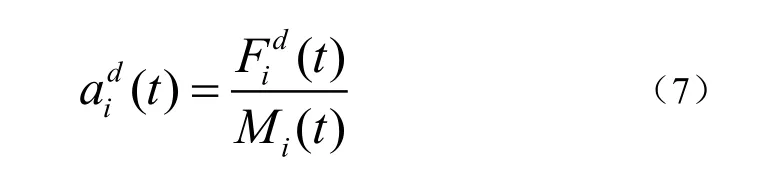
然后求取下一时刻的速度和位置信息如公式（8）、（9）：

另外，惯性质量也需要实时更新，它的大小与适应度函数相关，所表达的意思即惯性质量越大，就会产生越大的吸引力，也就越接近于所需要的最优值。其计算方法如公式（10）、（11）、（12）：

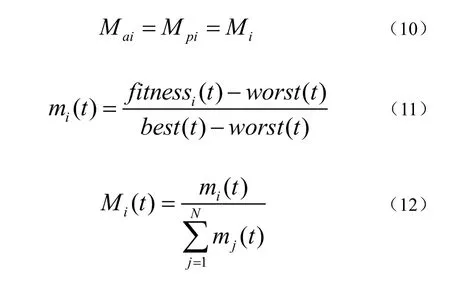
上式的fitnessi （t）代表的是当前时刻的适应度大小。如果需要求最小值，就可以得到公式（13）、（14）：

由于RSSI 定位的模型已知，就可以通过公式（15）作为它的适应度函数，即公式（15）：

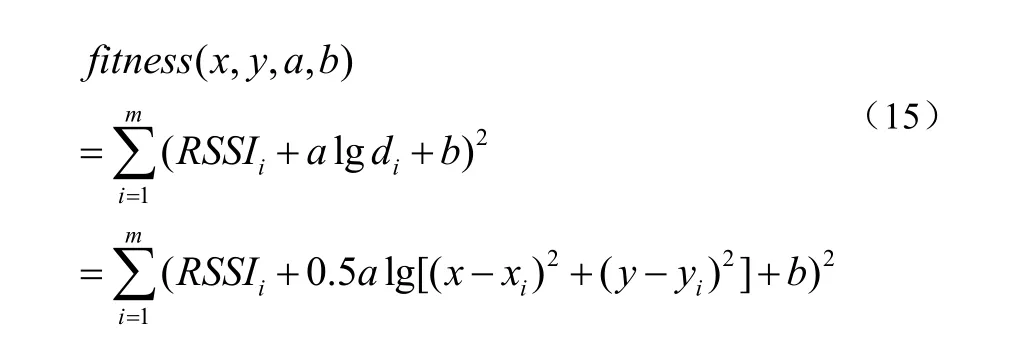
通过上述的 GSA方法训练出来的最终结果Xm（x，y，a，b），不仅得到了较为精确的定位结果，还实时得出RSSI定位模型中的参数a、b 。对于数学模型来说，环境所引起的变化正是通过参数a、b 得以表现，使用此方法实现对定位节点坐标以及模型参数动态的跟踪变化。

2 RSSI 定位系统的架构

由前面的定位算法可以得知，若需要对一个节点进行定位，需要至少三个参考节点的位置才可以确定定位节点的位置，此外还需要一个网关，主要负责网络的协调和服务，参考节点是已知位置信息的固定节点，而定位节点表示需要确定位置的节点。这里以4个参考节点为例，描绘出整个RSSI定位的系统架构如图1所示：

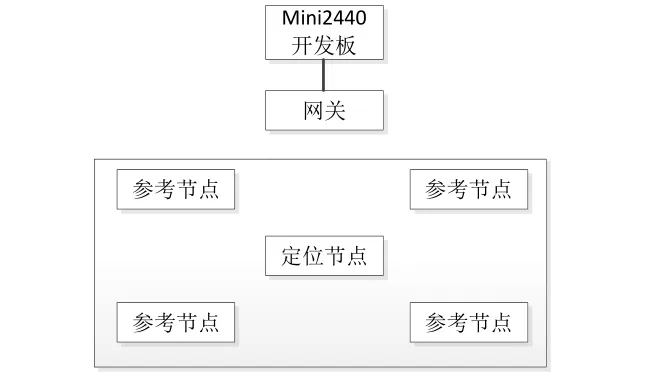
图1　RSSI 定位系统架构

将ZigBee 协议找下载进入CC2430 开发板，并且编写完运行于开发板上的应用程序，使得它们相互之间可以通信并可以取出相应的RSSI 值，然后将相关的位置信息和RSSI值通过CC2430 网关传递给mini2440 开发板，在开发板中进行相应的处理和运算并显示出所需要的节点信息。

3 RSSI 定位系统在消防中的应用

RSSI 定位系统在消防中可以应用的地方较为广泛，可以定位消防员，监控消防的特殊地点灯，本次定位实验的节点如图2所示：

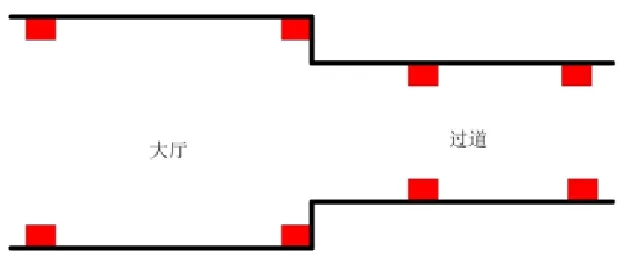
图2　参考节点的位置分布

在某消防的大厅和过道上进行，实验步骤主要是：在大厅和过道中放置参考节点，实验中的各个参考节点的主要位置如图2所示；打开网关、参考节点与定位节点，是其组成ZigBee的无线网络；移动定位节点，记录定位节点的位置信息；运行定位系统软件，记录该定位节点的3 次结果；求出本次定位的累加均方根误差。

上图节点放置于消防人流量较大的大厅和过道，可以看成是环境改变较大的情况，本文的定位系统较为适用。在9点，12 点和16 点分别运行该系统，按照上述的实验步骤进行定位定位实验，求出了对模型的参数估计，如表1所示：

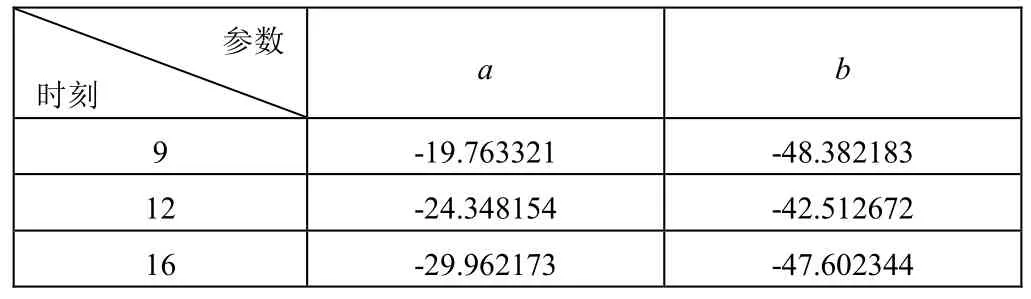
表1　本文算法对参数的估计

其累加均方根误差情况如表2 所示：

表2　定位系统的累加均方根误差

实验过程中定位的系统的运行较为稳定，能够实时显示出定位模型的参数和最终定位结果，说明系统能够成功地运行。从表1 中可以看出，RSSI 定位的模型参数是变化的，说明设计的定位系统能够实现参数的动态跟踪变化，表2 的数据显示了各时刻的累加均方根误差，总体处于较小的水平，基本达到了预期的效果，说明在消防的这种环境变化的情况下，该定位系统也能达到较为良好的效果。

4 总结

本文提出将引力搜索算法应用于RSSI 定位模型之中，提高了定位的精度，增强了系统对环境条件的适应能力，设计了相应的应用程序，取得了较为良好的效果。由于RSSI定位系统使用了ZigBee技术，而在物联网的应用中可以对本文的定位系统进行进一步的开发与设计，使得功能更加完善。

参考文献

[1] 谢晓佳,程丽君,王勇.基于ZigBee 网络平台的井下人员跟踪定位系统[J].煤炭学报,2007, 32(8): 884-888.

[2] 倪瑛,戴娟.ZigBee 定位技术的研究[J].南京工业职业技术学院学报,2013,13(2): 43-46.

[3] 魏立线,姚武军,钟卫东,等.基于LQI 的WSN 自适应差错控制方案[J].计算机工程,2011, 37(21): 64-67.

[4] 章坚武, 张璐, 应瑛, 等. 基于ZigBee 的RSSI 测距研究[J]. 传感技术学报, 2009, 22(2): 285-288.

[5] Sahu P K, Wu E H-K，Sahoo J. DuRT: Dual RSSI Trend Based Localization forWireless Sensor Networks [J]. IEEE SENSORS JOURNAL, 2013, 13(8): 3115-3123.

[6] Kuo R J, Shieh M C, Zhang J W, et al. The application of an artificial immune system-based back-propagation neural network with feature selection to an RFID positioning system[J]. Robotics and Computer-Integrated Manufacturing,2013, 29:431-438.

[7] Marti J V, Sales J, Marin R, et al. Multi-Sensor Localization and Navigation for Remote Manipulation in Smoky Areas[J]. Int J Adv Robotic Sy, 2013, 10(211): 1-8.

[8] Blumrosen G, Hod B, Anker T, et al. Enhanced calibration technique for RSSI-based ranging in body area networks[J]. Ad Hoc Networks, 2013, 11: 555-569

Application of RSSI Model Optimization Based on Gravitational Search Algorithm in Fire Location

Yang Yong
(Xiangyang Vocational and Technical College, Xiangyang 441050, China)

Abstract:The RSSI positioning method has been a research hot topic in recent years. In this paper, the corrected parameter of RSSI distance measurement model is calculated by using the maximum likelihood method, and the coordinates of the nodes required are calculated by using the least square method, then the coordinates and parameters estimated by using the least square method preliminary are optimized and amended by using the gravitation search algorithm, which can not only improve the precision of the node coordinates, but also track the dynamic variation of the position model parameters. The application program of RSSI positioning system is embedded into the fire protection positioning system, and the position of the reference node coming from the serial port is received by the network node, The RSSI value of the position node in received by the reference node, and the final position of positioning node is calculated by using the presented algorithm. Finally, the parameter optimization results of the positioning model are verified according to the results of the fire protection positioning. The overall error of the RSSI positioning system is less, and the parameter can reflect that the change of the environment and the result is good as expected.

Key words:Positioning; Gravitation Search Algorithm; Fire Protection; Wireless Network

收稿日期：（2015.09.21）

作者简介：杨 勇（1971-），男，湖北省襄阳职业技术学院，讲师，研究方向：网络综合布线和物联网，襄阳，441050

文章编号：1007-757X(2016)01-0066-04

中图分类号：TP311

文献标志码：A