一类神经元电路线性耦合同步研究

张壮志,任国栋,王宇峰

(兰州理工大学 理学院,甘肃 兰州　730050)



一类神经元电路线性耦合同步研究

张壮志,任国栋,王宇峰

(兰州理工大学 理学院,甘肃 兰州730050)

摘要为了研究混沌神经元的同步问题,利用Pspice软件设计了一类模拟神经电活动的神经元电路,对其封装后进一步研究该电路的线性耦合同步问题。通过调制耦合强度增益,发现当电路中耦合增益大于一定临界值就可以实现两个混沌神经元电路的同步。利用数值计算研究线性耦合同步来实现神经元同步,计算结果和电路模拟结果一致。

关键词Hindmarsh-Rose神经元;耦合电路;同步

近年来,人们研究了神经元的自适应同步,神经元系统的耦合同步[1-3]。神经元作为神经系统的基本结构和单位,以生物电的产生、变化、传播为特征,能够进行信息传递,是一个复杂的非线性动力系统。混沌同步是自然界中的一种自然现象[4-6],它通常指至少两个振动系统相位间的协调一致现象。从文献[7]中得知,关于同步现象最早的研究可以追溯到1673年惠更斯关于耦合单摆的同步现象的观察。实际上,若干个耦合单元之间通过相互作用达到同步的现象在许多领域中屡见不鲜。 同步现象不仅在自然界广泛存在,它在实际应用中更是非常重要的。尤其是20世纪90年代以来,佩拉卡和卡罗尔提出相同混沌子系统间,在不同的初始条件下,通过某种驱动(或耦合),仍然可以实现混沌轨道的同步化[8]。他们提出了一种混沌控制方法(P-C方法),并在电子线路上首次观察到混沌同步现象。他们的工作和OGY控制混沌的工作,极大地推动了混沌同步和混沌控制的理论研究,拉开了利用混沌的序幕。

近些年来,混沌同步的方法不断涌现,其应用领域也从物理学迅速扩展到生物学、化学、医学、电子学、信息科学和保密通信等领域[9]。由于混沌同步在工程技术上的重要价值和广阔的应用前景,它一直是非线性科学领域的研究热点课题之一。

1HR神经元结构

Hindmarsh-Rose(HR)神经元[10]系统的动力学方程为

(1)

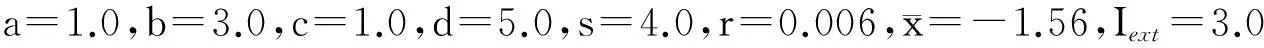
。时间步长选择0.01s。基于Pspice软件,单个神经元电路如图1所示。

驱动系统方程为

(2)

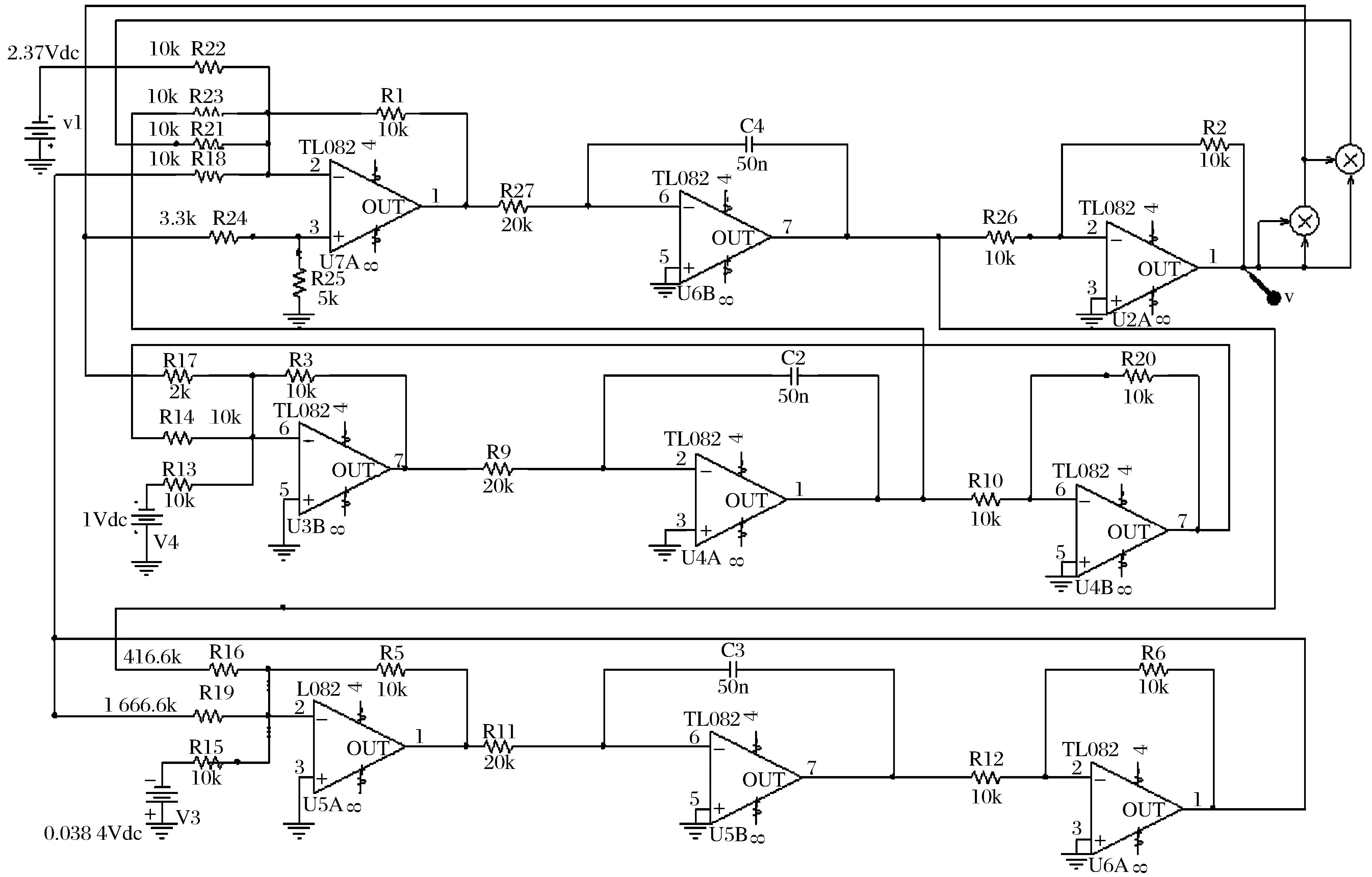
图1　单个神经元电路Fig.1　Circuit sketch map of single neuron

响应系统方程为

(3)

其中k为耦合强度。

两个神经元耦合电路如图2所示。

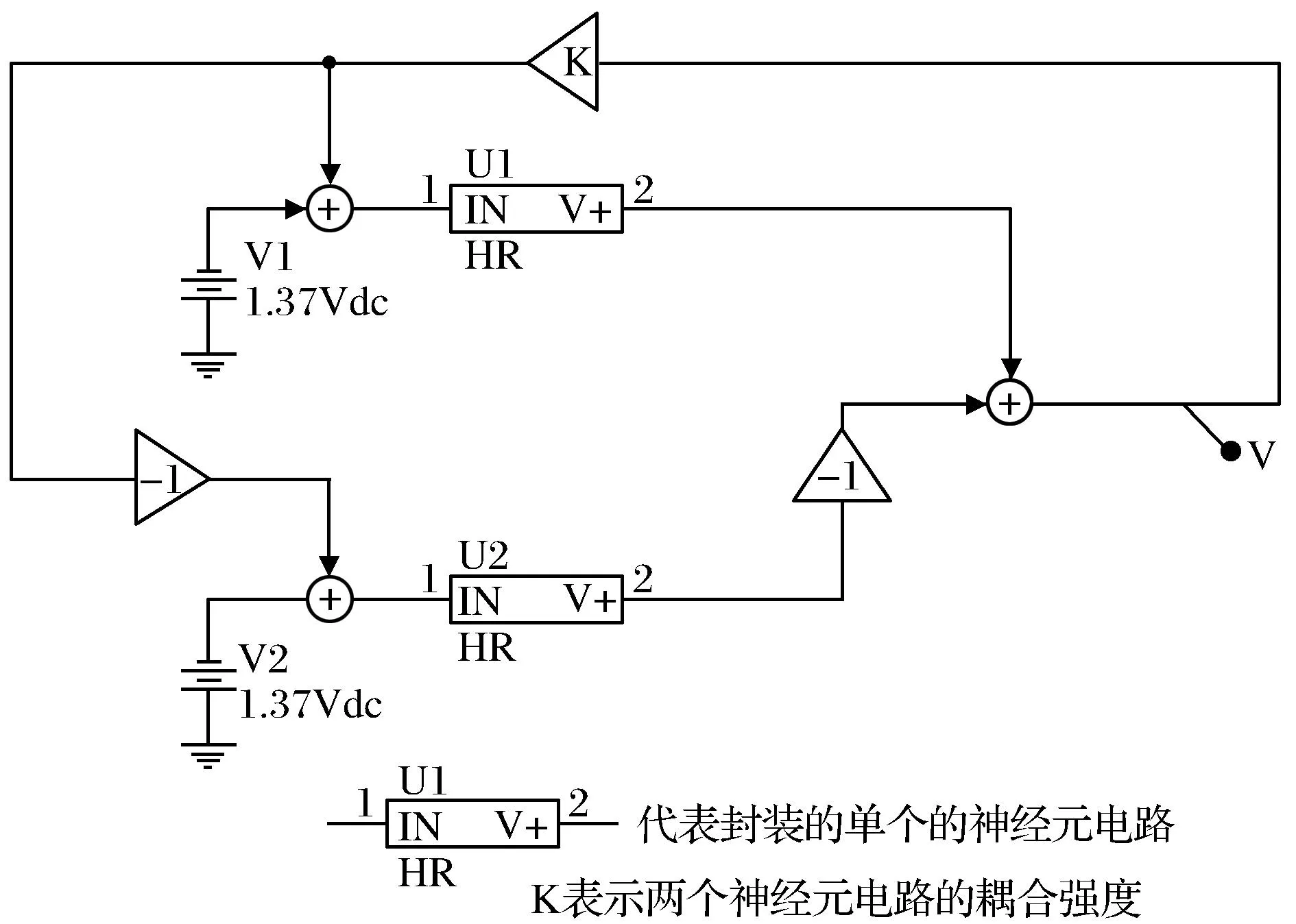
图2　两个神经元耦合电路Fig.2　Sketch map of two neuron coupling circuits

2仿真结果与分析

首先利用Pspice仿真单个神经元电路(k=0)的电位变化序列,单个神经元电路的Pspice输出见图3。

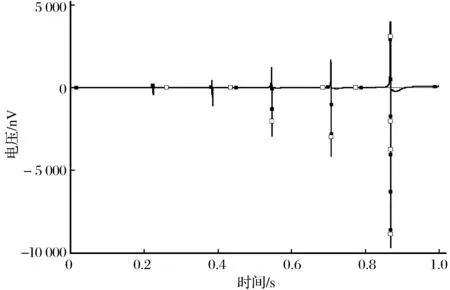
图3　单个神经元电路的Pspice输出Fig.3　Pspice output diagram of single neuron circuit

由图3可知,单个神经元电路两端输出电压随时间变化,可以看出电路输出电压取值在10-6~10-5V。选择不同的k作为增益,观察耦合电路系统是否达到同步。

k分别为0.1、0.5、1.0、1.5时两个神经元耦合电路两端输出电压见图4~图7。

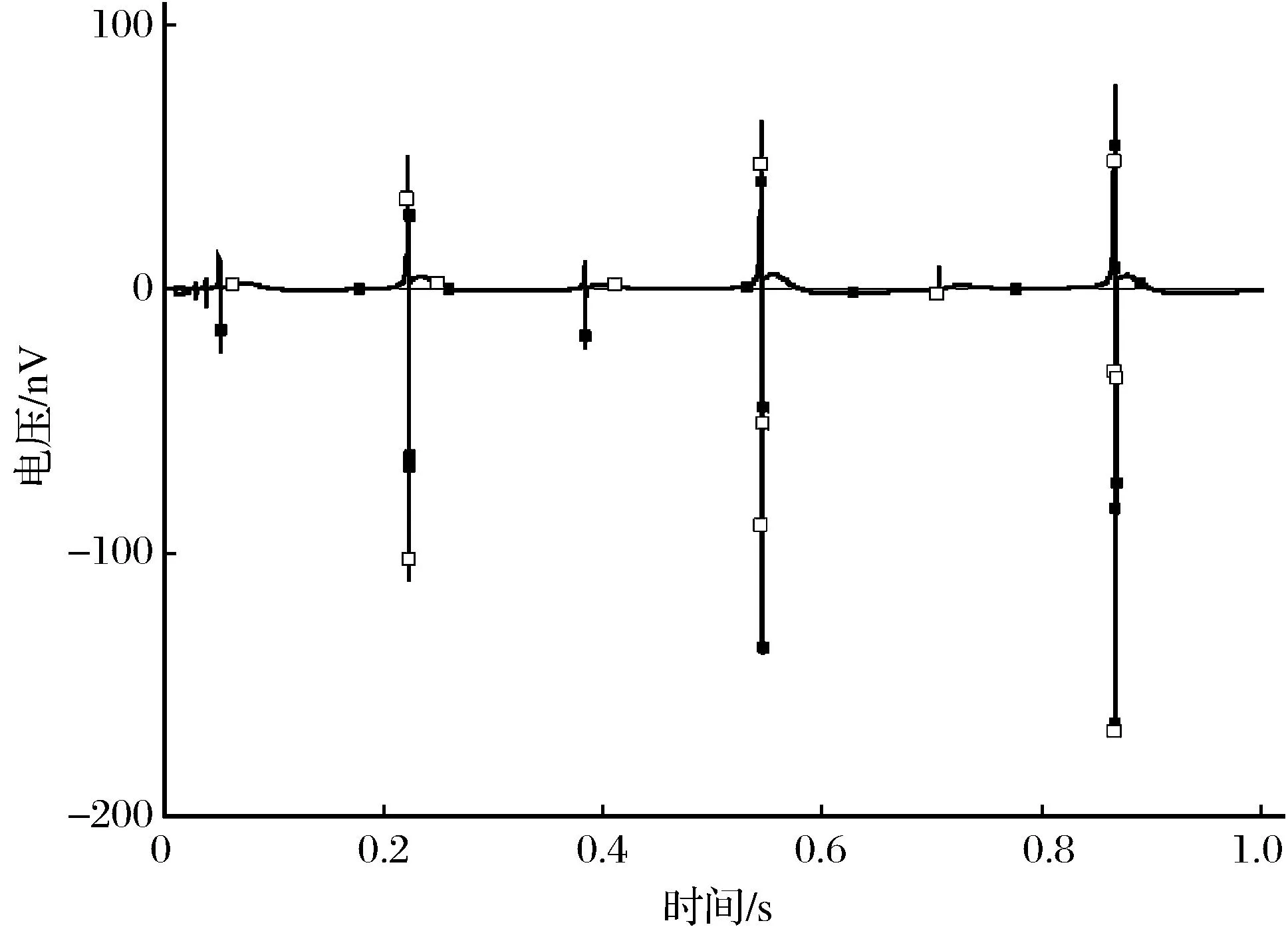
图4　k=0.1时两个神经元耦合电路两端输出电压Fig.4　Change of output voltages on two ends of twoneuron coupling circuits along with time when k=0.1

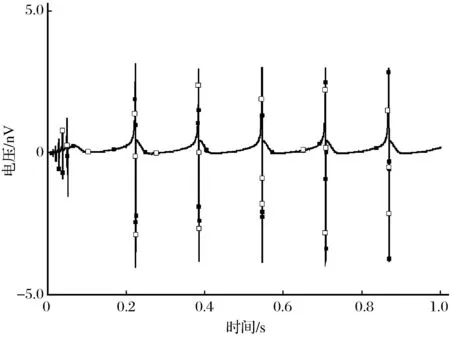
图5　k=0.5时两个神经元耦合电路两端输出电压Fig.5　Change of output voltages on two ends of twoneuron coupling circuits along with time when k=0.5

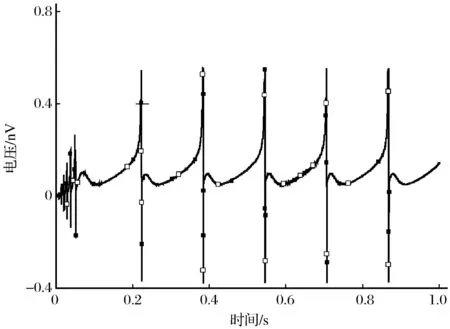
图6　k=1时两个神经元耦合电路两端输出电压Fig.6　Change of output voltages on two ends of twoneuron coupling circuits along with time when k=1

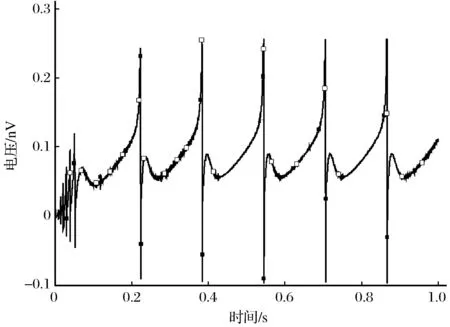
图7　k=1.5时两个神经元耦合电路两端输出电压 Fig.7　Change of output voltages on two ends of twoneuron coupling circuits along with time when k=1.5

由图4可知,k=0.1时系统输出电压为10-7V,与10-6~10-5V相差不大,耦合系统不同步。

由图5可知,k=0.5时系统输出电压为10-9V,与10-6~10-5V差别比较大,耦合系统接近于同步。

由图6可知,k=1时系统输出电压为10-10V,与10-6~10-5V相差明显,耦合系统达到同步。

由图7可知,k=1.5时系统输出电压为10-10V,与10-6~10-5V相差明显,耦合系统达到同步。利用Matlab软件进行数值计算来验证以上电路模拟结果。耦合强度k分别取0.1、0.2、0.3、0.4时,两个变量的差值如图8~图11所示。

由图8可知,k=0.1时系统不同步。

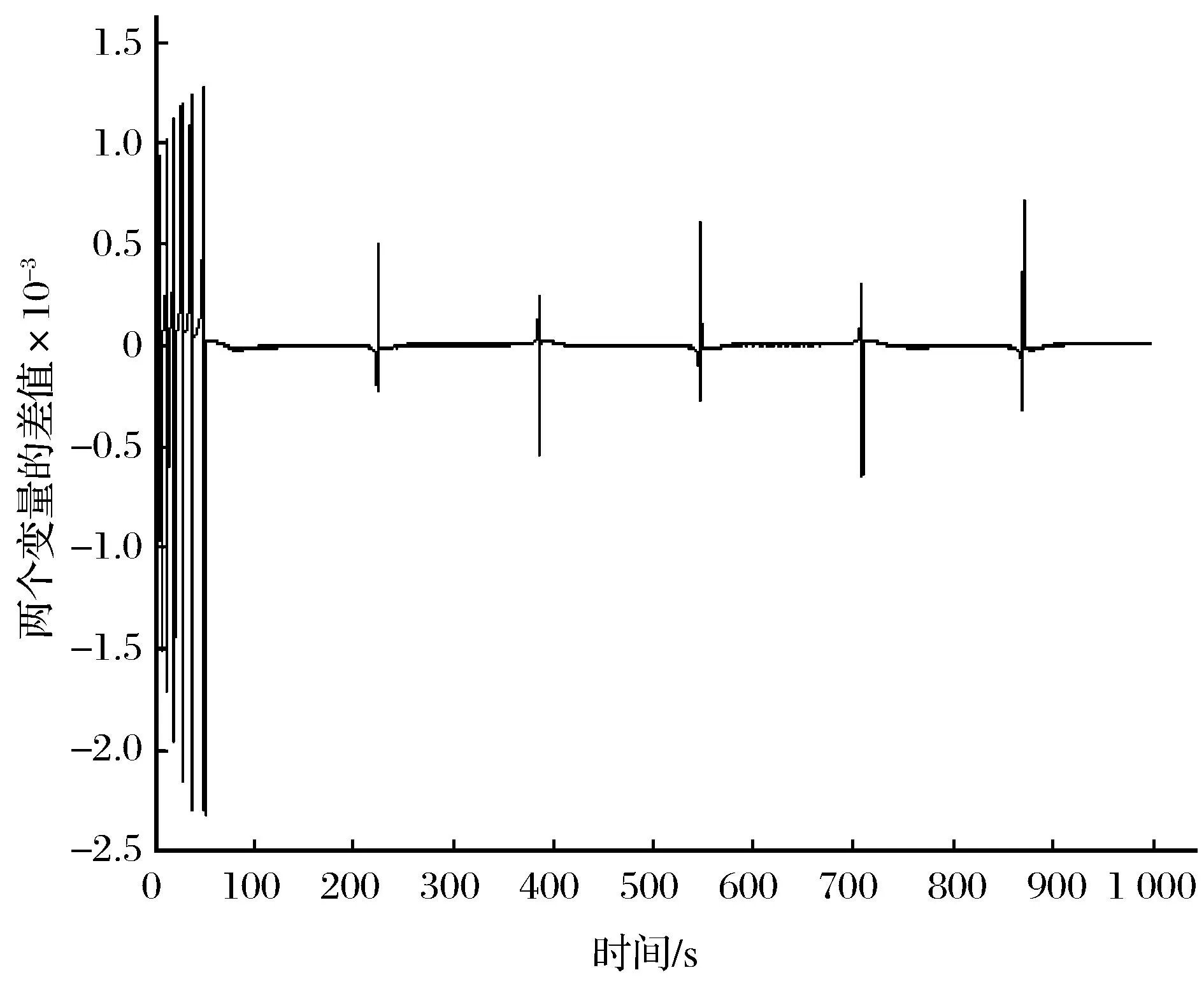
图8　k=0.1时两个变量的差值随时间的变化Fig.8　Change of difference of two variables alongwith time when k=0.1

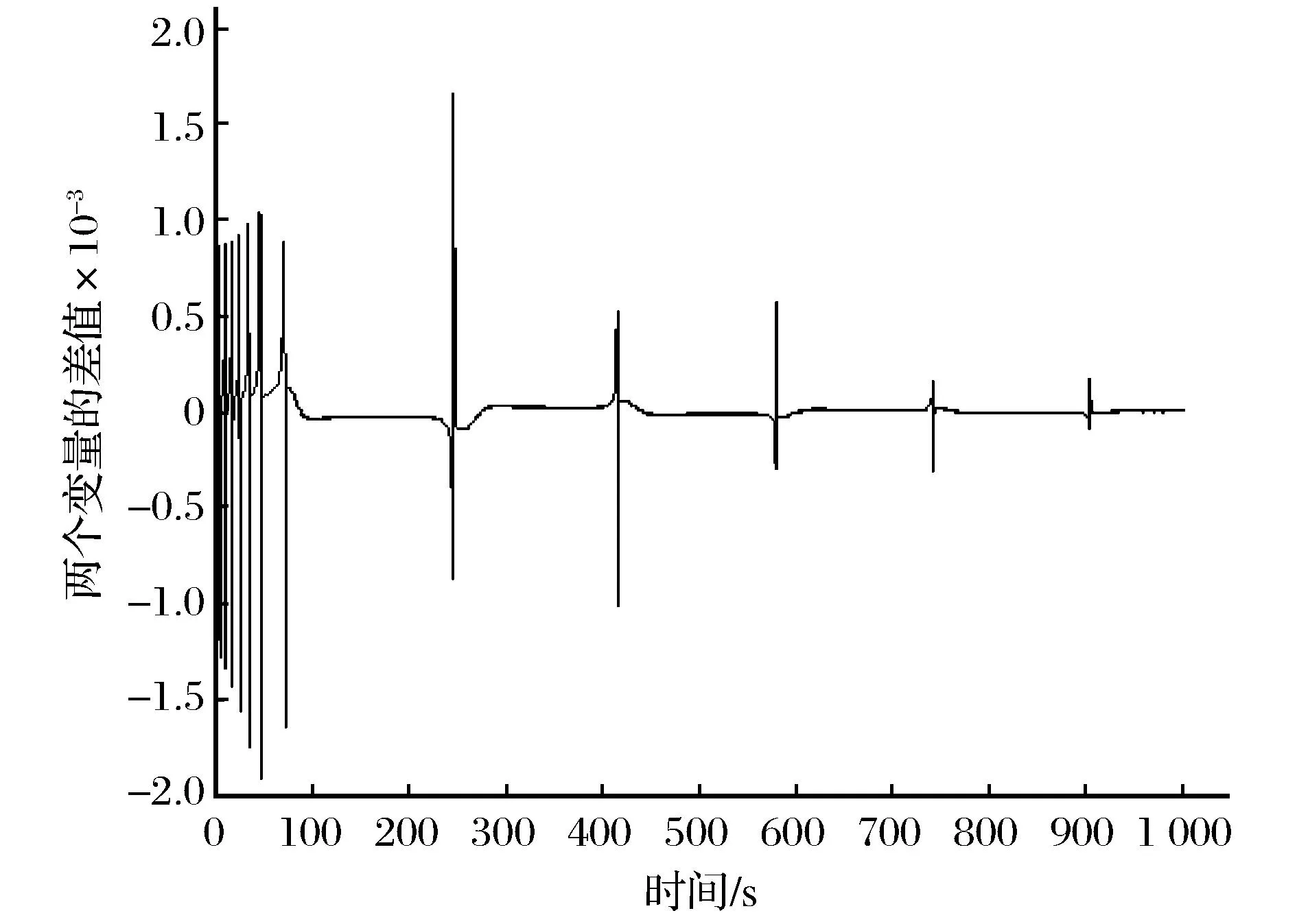
图9　k=0.2时两个变量的差值随时间的变化Fig.9　Change of difference of two variables alongwith time when k=0.2

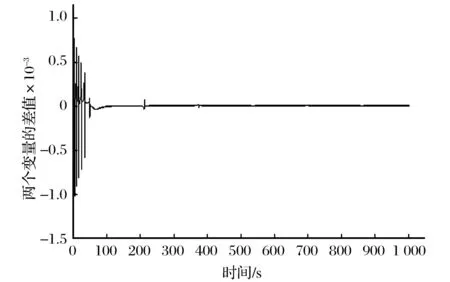
图10　k=0.3时两个变量的差值随时间的变化Fig.10　Change of difference of two variables alongwith time when k=0.3

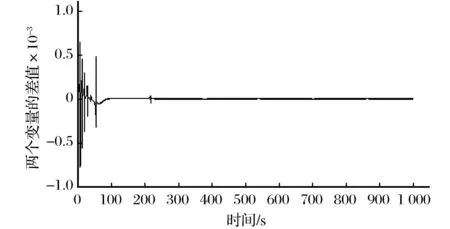
图11　k=0.4时两个变量的差值随时间的变化Fig.11　Change of difference of two variables alongwith time when k=0.4

由图9可知,k=0.2时系统不同步。

由图10可知,k=0.3时系统逐渐同步。

由图11可知,k=0.4时系统逐渐同步。数值计算结果表明,比较小的耦合强度如k取0.1、0.2时系统始终不同步,而比较大的耦合强度如k取0.3、0.4时容易使系统逐渐达到同步。

3结论

基于Pspice软件,设计了一类简化神经元Hindmarsh-Rose神经元电路,对两个封装的HR神经元电路线性耦合同步进行了研究。发现当神经元电路耦合增益比较小,两个电路不同步,逐渐增加耦合强度到临界值之上,两个混沌神经元电路则实现了完全同步。进一步基于Matlab软件,利用数值模拟验证了电路结果的可靠性。

参考文献:

[1]何继爱,黄智武,田亚菲.一种单神经元PID控制器[J].甘肃科学学报,2004,16(4):70-73.

[2]马军,苏文涛,高加振.Hindmarsh Rose混沌神经元自适应同步和参数识别的优化研究[J].物理学报,2010,78(3):1 554-1 561.

[3]彭军,廖晓峰,吴中福.一个延时混沌神经元系统的耦合同步[J].电子与信息学报,2003,25(1):123-127.

[4]杨涛,邵惠鹤. 一类混沌系统的同步方法[J].物理学报,2002,70(4):742-748.

[5]王铁邦,覃团发,陈光旨.超混沌系统的耦合同步[J].物理学报,2001,69(10):1 851-1 855.

[6]俞翔,朱石坚,刘树勇. 广义混沌同步中的多稳定同步流形[J].物理学报,2008,76(5):2 761-2 769.

[7]王念川.简单耦合系统和耦合摆同步的实验研究[D]. 北京:北京邮电大学,2012.

[8]徐克生,张伟东,唐国宁. Hindmarsh-Rose神经元模型的单变量控制同步与反同步[J].广西师范大学学报:自然科学版,2010,28(4):5-8.

[9]于娜,丁群,陈红. 异结构系统混沌同步及其在保密通信中的应用[J].通信学报,2007,28(10):73-78.

[10]林晨,于洪洁.延迟-完全连接H-R神经网络的同步[J].上海交通大学学报,2008,53(6):1 017-1 021.

Study of Linear Coupling and Synchronization of A Class of Neuron Circuits

Zhang Zhuangzhi,Ren Guodong,Wang Yufeng

(DepartmentofPhysics,LanzhouUniversityofTechnology,Lanzhou730050,China)

AbstractA class of neuron circuits simulating activities of neuroelectricity was designed by using Pspice software to further research linear coupling and synchronization of two neuron circuits after encapsulation in order to research the synchronization problem of the neuron. It found that synchronization of two chaotic neuron circuits could be realized when the coupling gain in the circuit was greater than the critical value by modulating the coupling intensity gain. Further,the linear coupling was further studied by using numerical calculation to carry out neuron synchronization,wherein the result of numerical calculation was consistent with that of circuit simulation.

Key wordsHindmarsh-Rose neuron;Coupling circuit;Synchronization

中图分类号:O415.5

文献标志码:A

文章编号:1004-0366(2016)01-0061-05

作者简介:张壮志(1987-),男,山西临汾人,硕士研究生,研究方向为非线性物理.E-mail:592047326@qq.com.

收稿日期:2015-03-10;修回日期:2015-06-17.

doi:10.16468/j.cnki.issn1004-0366.2016.01.014.

引用格式:Zhang Zhuangzhi,Ren Guodong,Wang Yufeng.Study of Linear Coupling and Synchronization of a Class of Neuron Circuits[J].Journal of Gansu Sciences,2016,28(1):61-64,104.[张壮志,任国栋,王宇峰.一类神经元电路线性耦合同步研究[J].甘肃科学学报,2016,28(1):61-64,104.]