双参数有界算子C群与双参数C半群的关系

薛　双,赵华新,薛风风

(延安大学 数学与计算机科学学院,陕西 延安　716000)



双参数有界算子C群与双参数C半群的关系

薛双,赵华新,薛风风

(延安大学 数学与计算机科学学院,陕西 延安716000)

摘要在Banach空间上,根据双参数有界算子C群及它的无穷小生成元的概念,与双参数C半群及它的无穷小生成元的概念,利用概念之间的关系,证明了双参数有界算子C群与双参数C半群的关系。

关键词双参数;有界算子C群;C半群

根据文献[1-4]中双参数C半群及它的无穷小生成元的概念,定义了双参数有界算子C群及它的无穷小生成元的概念,利用概念之间的关系,证明了双参数有界算子C群与双参数C半群的关系。

研究中的空间X是Banach空间,所有算子是有界线性算子,C表示X上有界单射算子,B(X)表示X上所有的有界线性算子,D表示A1A2在X上的定义域。

(1)T(0,0)=C;

(2)CT((s1,t1)+(s2,t2))=T(s1,t1)T(s2,t2),∀s1,s2,t1,t2∈R;

(3)映射(s,t)→T(s,t)x 强连续,∀s,t∈R;∀x∈X,

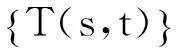
下面证明双参数有界算子C群与双参数C半群的关系。

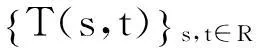
当s,t≥0时,我们把T(s,t)记作T1(s,t),下面验证T1(s,t)是双参数C半群,其无穷小生成元是(A1,A2)。

(1)T1(0,0)=T(0,0)=C;

(2)T1((s1,t1)+(s2,t2))=T((s1,t1)+(s2,t2))=CT(s1,t1)T(s2,t2)=CT1(s1,t1)T1(s2,t2);

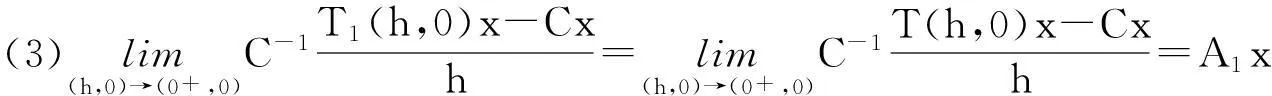
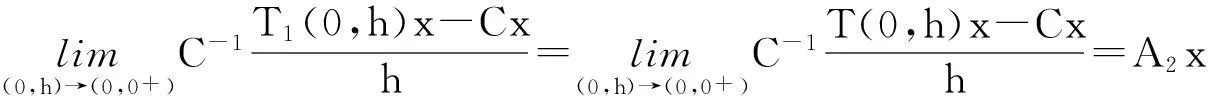
所以T1(s,t)是双参数C半群,其无穷小生成元是(A1,A2)。

当s,t≤0时,我们把T(s,t)记作T2(s,t)。设T2(s,t)=T(-s,-t) ,同理可证T2(s,t)是双参数C半群,其无穷小生成元是(-A1,-A2),证毕。

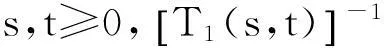
证明对于∀s,t≥0,都有

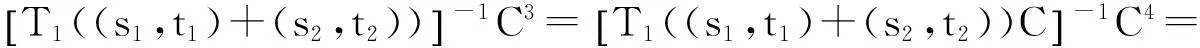
T2(s1,t1)T2(s2,t2),∀s1,t1,s2,t2≥0

从而验证T2(s,t)是双参数C半群。又因为对∀x∈D,有

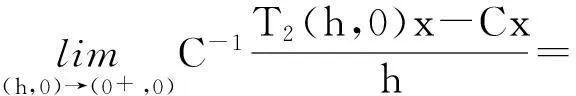
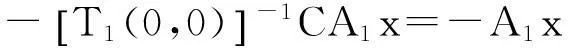
故T2(s,0)满足双参数C半群的定义,且其无穷小生成元是-A1。另有

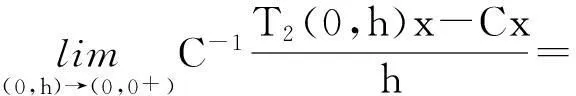
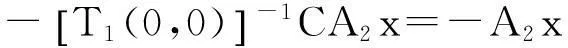
故T2(0,t)满足双参数C半群的定义,且其无穷小生成元是-A2。

从而T2(s,t)满足双参数C半群的定义,其无穷小生成元是(-A1,-A2)。

综上所述,T1(s,t),T2(s,t)是双参数C半群,其无穷小生成元分别是(A1,A2),(-A1,-A2)。

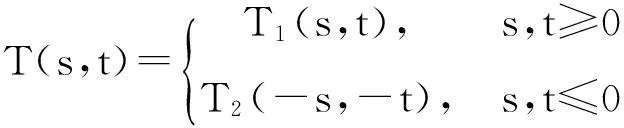
(1)T(0,0)=T1(0,0)=T2(0,0)=C;

(2) 当∀s1,t1,s2,t2≥0时,有

T((s1,t1)+(s2,t2))=T1((s1,t1)+(s2,t2))=CT1(s1,t1)T1(s2,t2)=CT(s1,t1)T(s2,t2),

当∀s1,t1,s2,t2≤0时,有

T((s1,t1)+(s2,t2))=T2((s1,t1)+(s2,t2))=CT2(s1,t1)T2(s2,t2)=CT(s1,t1)T(s2,t2),

得

T((s1,t1)+(s2,t2))=C(s1,t1)T(s2,t2),∀s1,t1,s2,t2∈R;

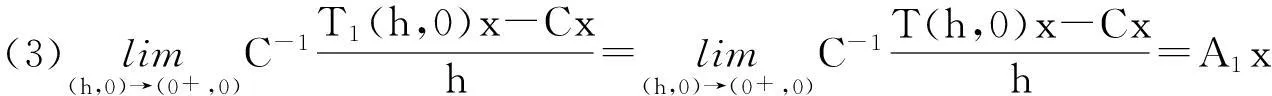
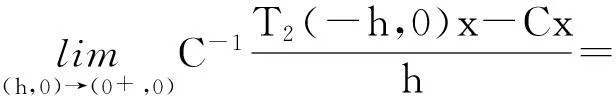
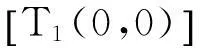
得出

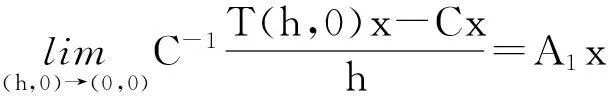
同理可证

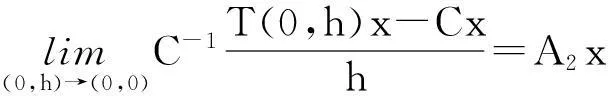
综上所述,T(s,t)是双参数有界算子C群,其无穷小生成元是(A1,A2),证毕。

参考文献:

[1]徐敏,赵华新,赵拓.双参数C半群的一些结果[J].沈阳师范大学学报:自然科学版,2013,31(3):363-366.

[2]赵拓,赵华新,徐敏.C半群和双参数C半群的指数公式[J].天津师范大学学报:自然科学版,2013,33(4):13-15.

[3]赵华新,李晓爱.C-半群的可逆性与C-群[J].延安大学学报:自然科学版,1997,16(2):10-13.

[4]黄翠,王彩侠,张明翠,等.双参数C-半群[J].纯粹数学与应用数学,2013,29(3):299-305.

[5]刘瑞,赵华新,马强强,等.广义C0算子群[J].延安大学学报:自然科学版,2009,28(4):3-5.

[6]徐敏,赵华新,赵拓.双参数C半群Yosida逼近的应用[J].江西科学,2013,31(5):580-582.

[7]蔡亮,宋晓秋,李玉霞.双参数C0有界算子群[J].黑龙江科技学院学报,2011,21(1):77-80.

[8]陈文忠.C-无穷小生成元的表示式[J].厦门大学学报:自然科学版,1993,32(2):135-140.

Relationship of Biparameter Bounded Operator GroupCand Biparameter SemigroupC

Xue Shuang,Zhao Huaxin,Xue Fengfeng

(CollegeofMathematicsandComputerScience,Yan’anUniversity,Yan’an716000,China)

AbstractThe relationship of biparameter bounded operator groupCand biparameter semigroupCwas proved by using the relationship among the concepts in the Banach space according to the concepts of biparameter bounded operator groupCand infinitesimal generator thereof,as well as the concepts of biparameter bounded operator semigroupCand infinitesimal generator thereof.

Key wordsBiparameter;Bounded operator groupC;SemigroupC

中图分类号:O177.2

文献标志码:A

文章编号:1004-0366(2016)01-0029-03

作者简介:薛双(1990-),女,陕西清涧人,硕士研究生,研究方向为应用泛函分析.E-mail:602539891@qq.com.

基金项目:陕西省教育厅专项科研计划项目(2013JK0570);延安大学自然基金项目(YDZ2013-03).

收稿日期:2015-04-07;修回日期:2015-07-11.

doi:10.16468/j.cnki.issn1004-0366.2016.01.007.

引用格式:Xue Shuang,Zhao Huaxin,Xue Fengfeng.Relationship of Biparameter Bounded Operator GroupCand Biparameter SemigroupC[J].Journal of Gansu Sciences,2016,28(1):29-31.[薛双,赵华新,薛风风.双参数有界算子C群与双参数C半群的关系[J].甘肃科学学报,2016,28(1):29-31.]