基于SVR的上海市商品房价格预测

袁秀芳,郑伯川,焦伟超

(西华师范大学 数学与信息学院,四川 南充　637009)



基于SVR的上海市商品房价格预测

袁秀芳,郑伯川,焦伟超

(西华师范大学 数学与信息学院,四川 南充637009)

摘要商品房价格受诸多因素影响,研究因素与商品房价格的关系是当前研究房价的一个热点。从1998—2013年的上海市商品房基本信息中,选取了对商品房价格产生影响的8个因素,利用LIBSVM工具建立了基于SVR的商品房价格预测模型,并对1998—2013年的商品房价格进行预测。实验表明,SVR模型比ARIMA模型具有更好的预测值,预测能力更强。

关键词商品房价格;ARIMA;SVR;预测

在市场经济条件下,具有经营资格的房地产开发公司通过出让方式取得土地使用权后经营的住宅就是商品房,其价格由成本、税金、利润、代收费用以及地段、层次、朝向、质量、材料差价等组成。进入21世纪以后,商品房价格不断上涨,房价已经成为关乎国计民生的问题,对商品房价格的研究也成为了学术界的一个热点。孔凡文等[1]采用直线趋势法和一元线性回归法预测沈阳市商品房价格,刘悦婷等[2]基于MATLAB建立多元线性回归模型预测兰州市商品住宅价格,武秀丽等[3]采用时间序列预测房价,常振海等[4]采用非参数自回归预测房价,陈森君[5]采用BP神经网络预测房价,徐富强[6]采用神经网络组合预测合肥市房价,陈博[7]采用灰色GM(1,1)模型预测西安市商品房价格。目前,支持向量回归(SVR,support vector regression)机被认为是预测能力十分出色的工具,它通过引入一个损失函数,将 SVR回归问题转化成对偶问题进行求解,克服了最小二乘回归方法的过拟合问题,在时间序列预测上得到了更为精准的结果。不仅如此,SVR不受数据区间较短的影响,能在数据样本较小的情况下建立良好的模型,采用原始数据建模即可,具有较高的泛化能力和预测精度。因此,我们采用SVR预测模型对上海市商品房价格进行预测,并与自回归求和移动平均(ARIMA,autoregressive integrated moving average)模型的预测结果进行对比。

1基于SVR模型的房价预测

1.1数据选取

1998年中国住房市场发生了变革,那么1998年就是商品房价格的一个分水岭,故从1998年的数据开始进行研究,从供给和需求[8,9]两个方面选取了8个影响上海市商品房价格的因素,通过1999—2014年的《上海市统计年鉴》[10]得到1998—2013年房地产价格相关数据,见表1。表1中X1为上海市生产总值(亿元);X2为上海市居民消费价格指数;X3为上海市土地交易价格指数;X4为上海市房屋租赁价格指数;X5为上海市建筑业总产值(亿元) ;X6为上海市房屋竣工面积(万m2);X7为上海市恩格尔系数;X8为上海市房地产住宅投资总额(亿元)。上海市单位面积商品房价格Y(元)=商品房销售额/商品房销售面积。

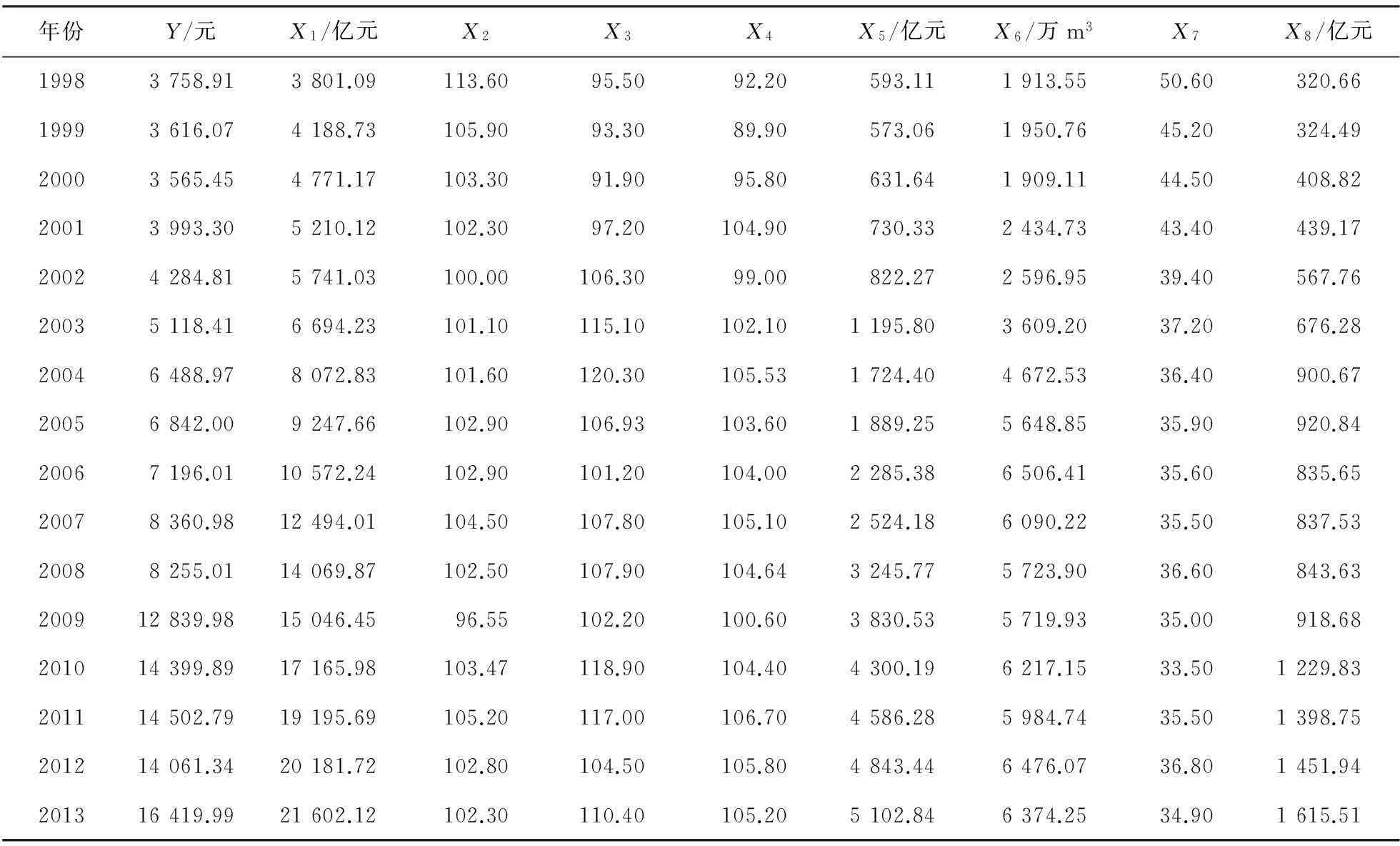
表1　上海市1998—2013年商品房基本信息

1.2数据归一化处理

以1998—2013年的Y、X1、X2、X3、X4、X5、X6、X7和X8的时间序列为SVR预测模型的输入变量,以Y的时间序列作为目标向量建立商品房价格预测模型。为消除各时间序列之间不同量纲的影响,对数据做归一化处理,使得每一时间序列向量在区间[0,1]之间,采用公式为

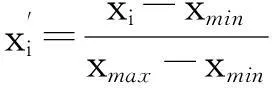
(1)

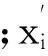
1.3房价预测步骤

采用以下步骤进行房价预测:

(1)数据归一化处理;

(3)利用LIBSVM软件工具[11]的svmtrain函数,选择ε-SVR算法和径向基核函数,对表1中选定的样本数据进行学习,得到回归模型。通过反复实验和效果对比,发现参数在一定范围内取值时,不同参数下的实验结果相差很小。因此,实验表明取多组不同参数都能得到相似的结果,上述实验结果所选用参数值为:g=0.2,c=10,p=0.005,e=0.001。其中:g表示多项式、径向基函数(RBF,radial basis function)和sigmoid核函数中的γ系数;c表示ε-SVR中的惩罚系数;p为ε-SVR的损失函数p的值;e为允许的终止判据;

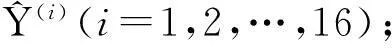
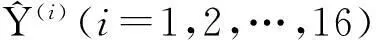
2实验结果

首先采用房价预测步骤对表1的数据进行实验,得到SVR模型的预测值和真实值的对比图和绝对百分比误差,结果见图1和表2。然后使用Eviews 7.2软件对表1中的Y建立ARIMA模型[12],得到Y的预测值和真实值的对比图和绝对百分比误差,结果见图1和表2。根据图1可知,两种模型的预测效果都比较好,但ARIMA模型的预测曲线波动比较大,SVR模型的预测曲线更接近真实值。

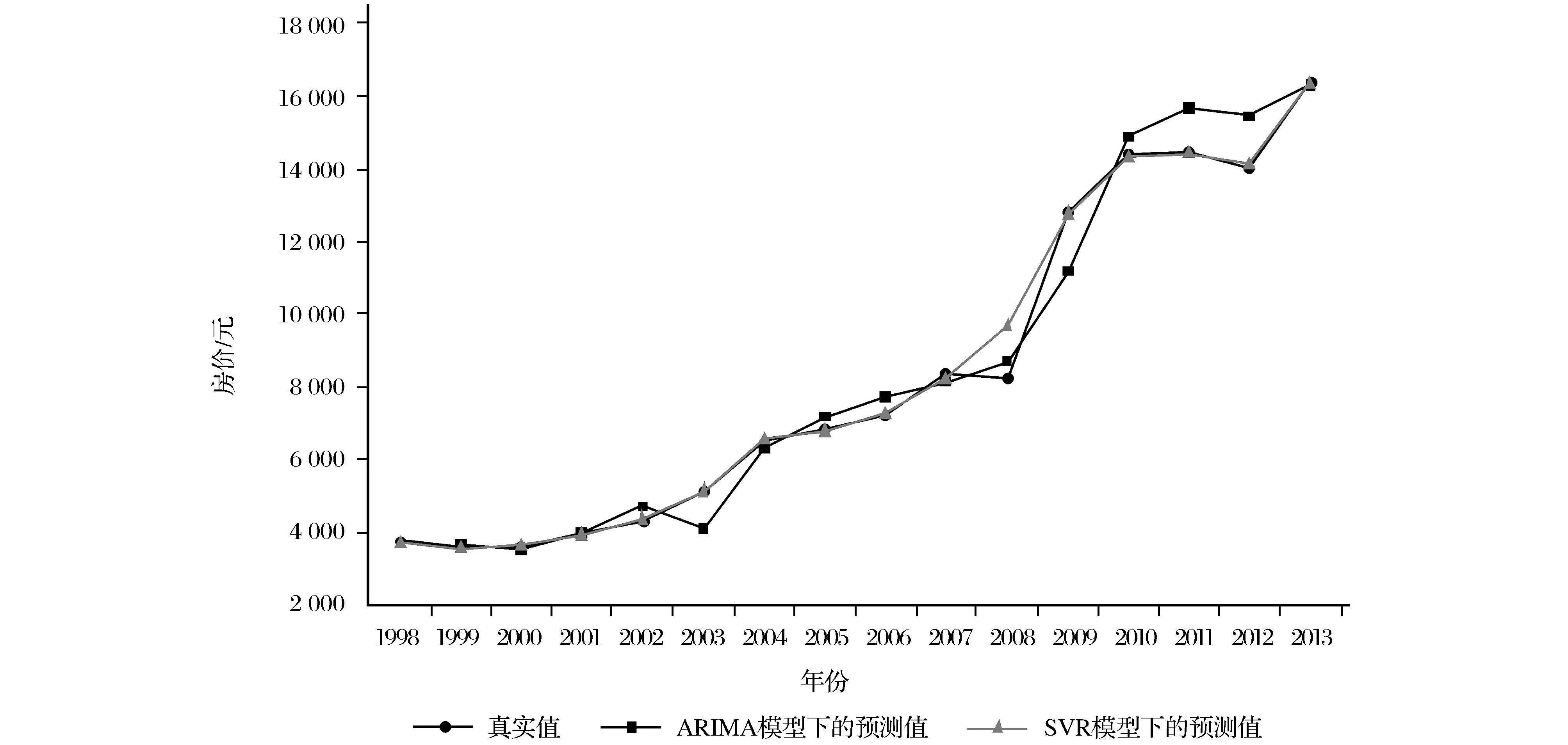
图1　商品房价格真实值以及两种模型下的预测值对比Fig.1　Comparison diagram of actual value of commodity house price and forecasting values under two models

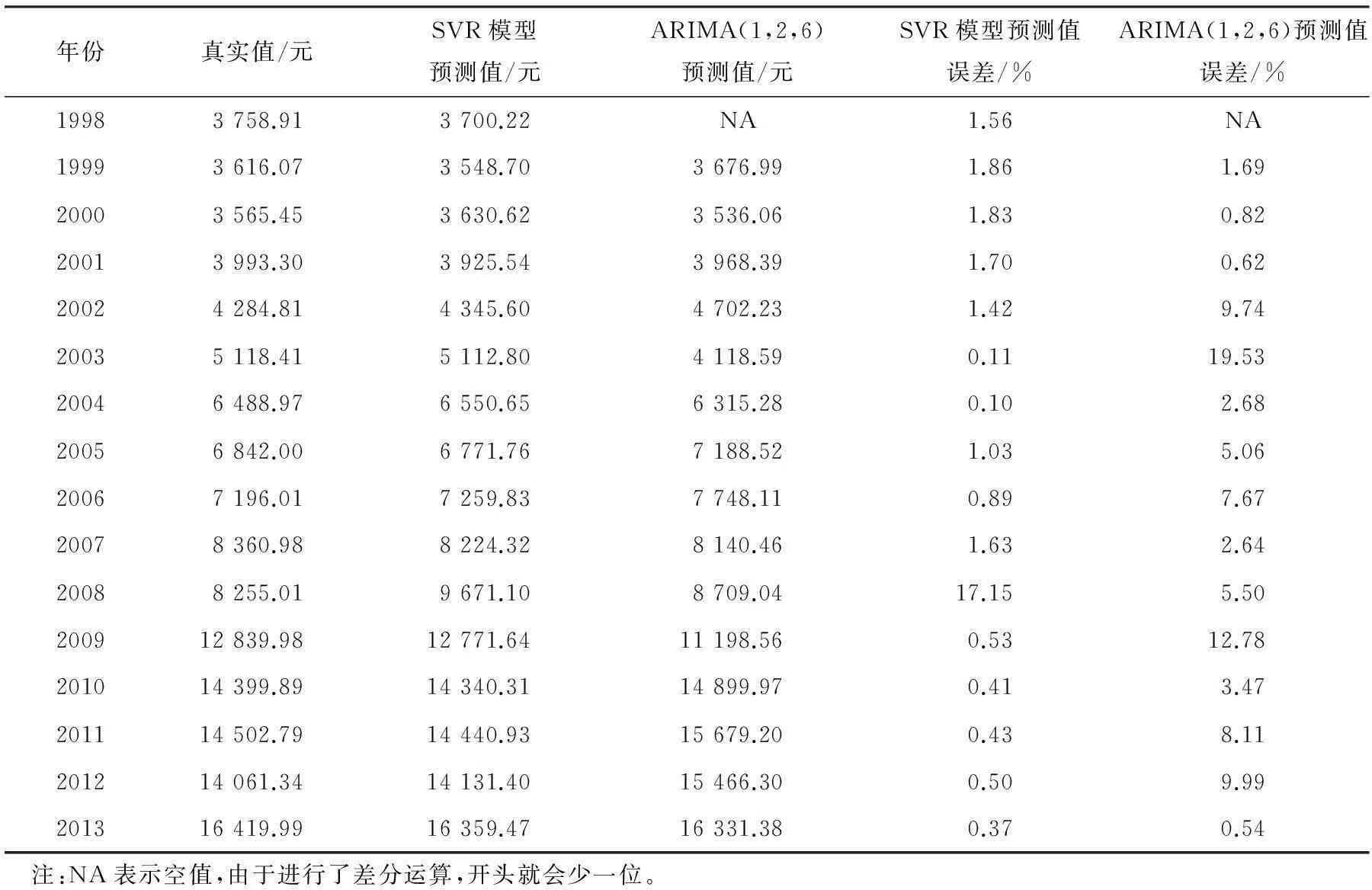
年份真实值/元SVR模型预测值/元ARIMA(1,2,6)预测值/元SVR模型预测值误差/%ARIMA(1,2,6)预测值误差/%19983758.913700.22NA1.56NA19993616.073548.703676.991.861.6920003565.453630.623536.061.830.8220013993.303925.543968.391.700.6220024284.814345.604702.231.429.7420035118.415112.804118.590.1119.5320046488.976550.656315.280.102.6820056842.006771.767188.521.035.0620067196.017259.837748.110.897.6720078360.988224.328140.461.632.6420088255.019671.108709.0417.155.50200912839.9812771.6411198.560.5312.78201014399.8914340.3114899.970.413.47201114502.7914440.9315679.200.438.11201214061.3414131.4015466.300.509.99201316419.9916359.4716331.380.370.54注:NA表示空值,由于进行了差分运算,开头就会少一位。

根据表2可知SVR模型在2008年商品房价格预测值与真实值相差较大,其他年份的预测值与真实值比较接近。查阅相关资料可知造成2008年预测值偏差大有两个原因:一是由于2008年宏观经济形势恶化、房地产行业呈现衰退局面;二是2007年国家多次提出加息政策调控住房民生问题,在2008年得到了集中体现,导致房价出现空前下降。除此之外,比较两种模型的预测值绝对百分比误差,大致上可见ARIMA模型的预测值绝对百分比误差更大更波动一些,反之SVR模型的预测值绝对百分比误差更小更均匀,所以SVR模型的预测效果比较好。为进一步对比SVR模型和ARIMA模型的预测效果,计算预测值绝对百分比误差的均值和标准差,计算公式为

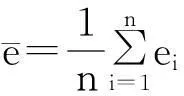
(2)

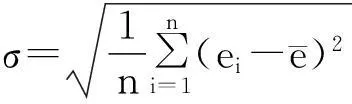
(3)

表3　预测结果的均值和标准差

由表3可知SVR模型预测值的绝对百分比误差均值和标准差都小于ARIMA模型,说明SVR模型预测值更接近于真实值。因此得出基于SVR模型的拟合精度很高,能够较好地拟合出商品房房价的走势。该模型在处理类似小样本多影响因素的预测分析中呈现了很大的优势和参考价值,能够为我国政府部门、宏观经济工作者及房地产相关人员提供参考和指导。

3结语

通过建立一种误差较小、回归效果理想的SVR商品房房价预测模型,与ARIMA模型的实验结果进行对比,得出了SVR模型的预测效果更好,预测能力更强的结论。该模型不仅为预测商品房价格提供了一种有效的方法,同时也通过实例体现了解决回归问题的优越性。

参考文献:

[1]孔凡文,李忠利,张春雨.沈阳市商品房价格预测分析[J].沈阳建筑大学学报:自然科学版,2001,23(3):232-234,238.

[2]刘悦婷,郑卓.基于MATLAB的兰州市商品住宅价格变动分析预测[J].甘肃科学学报,2011,23(3):155-158.

[3]武秀丽,张锋.时间序列分析法在房价预测中的应用——以广州市的数据为例[J].科学技术与工程,2007,7(21):5 631-5 635.

[4]常振海,刘薇.基于非参数自回归模型的房价预测[J].天水师范学院学报,2010,30(2):56-58.

[5]陈森君.中国商品房价格的影响因素分析及价格预测[D].武汉:华中科技大学,2008.

[6]徐富强.神经网络组合预测模型及其在房价趋势中的应用[D].合肥:安徽大学,2011.

[7]陈博.西安市商品房价格趋势的研究及其预测[D].西安:西安建筑科技大学,2012.

[8]曹玉.我国商品房价格影响因素研究[D].昆明:云南大学,2011.

[9]董艳芳.我国商品房价格形成的主要因素及形成机制分析[J].软科学,2012,26(6):96-98.

[10]上海市统计局.上海市统计年鉴[M].北京:中国统计出版社,1999-2014.

[11]Chang Chihchung,Lin Chihjen.LIBSVM :a Library for Support Vector Machines[EB/OL].http://www.csie.edu.tw/~cjlin/libsvm/,2015-06-22.

[12]王黎明,王连,杨楠.应用时间序列分析[M].上海:复旦大学出版社,2012.

SVR-based Price Forecasting of Commodity House in Shanghai

Yuan Xiufang,Zheng Bochuan,Jiao Weichao

(CollegeofMathematicandInformation,ChinaWestNormalUniversity,Nanchong637009,China)

AbstractThe price of the commodity house may be influenced by many factors;and study on relationship between the factors and the price of the commodity house is deemed as one hot issue in research of house price so far.The SVR-based commodity house price forecasting model was set up and the prices of the commodity house from 1998 to 2013 was forecasted by using LIBSVM tool after selecting eight factors generating influence to the price of the commodity house from the basic information of the commodity house in shanghai from 1998 to 2013.The experiments showed that SVR model,compared with the ARIMA model,had more excellent forecasting value and stronger forecasting ability.

Key wordsPrice forecasting of commodity house;ARIMA;SVR;Forecasting

中图分类号:O29

文献标志码:A

文章编号:1004-0366(2016)01-0025-04

作者简介:袁秀芳(1990-)，女，陕西延安人，硕士，研究方向为统计回归分析和支持向量机.E-mail:1141512393@qq.com.通讯作者:郑伯川.E-mail:80700399@qq.com.

基金项目:四川省教育厅自然科学重点项目(12ZA172)；西华师范大学启动基金(12B023).

收稿日期:2015-05-25;修回日期:2015-07-13.

doi:10.16468/j.cnki.issn1004-0366.2016.01.006.

引用格式:Yuan Xiufang,Zheng Bochuan,Jiao Weichao.SVR-based Price Forecasting of Commodity House in Shanghai[J].Journal of Gansu Sciences,2016,28(1):25-28.[袁秀芳,郑伯川,焦伟超.基于SVR的上海市商品房价格预测[J].甘肃科学学报,2016,28(1):25-28.]