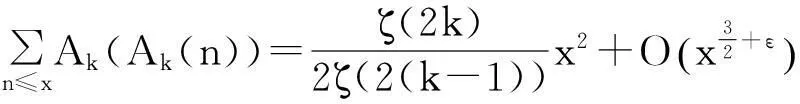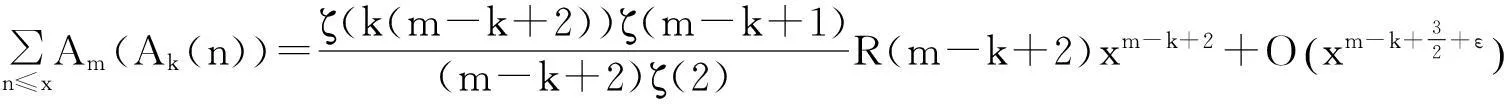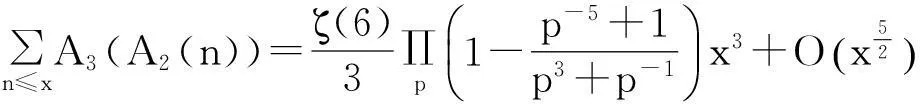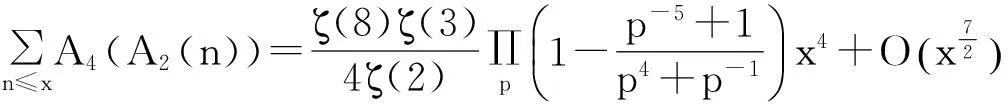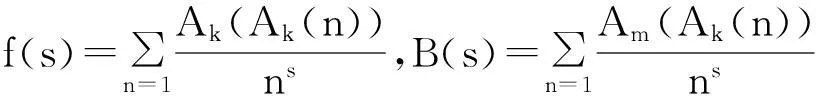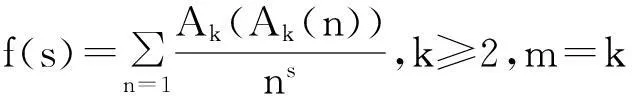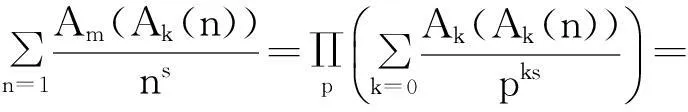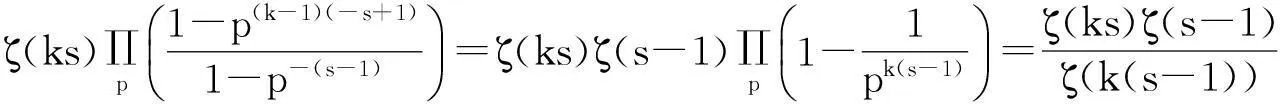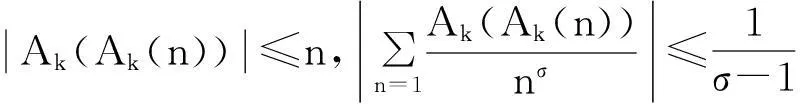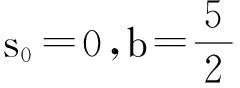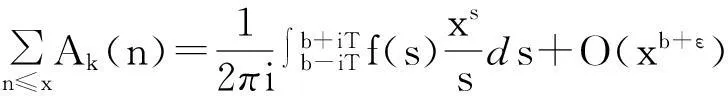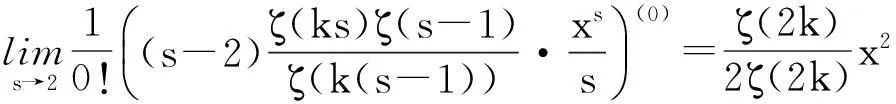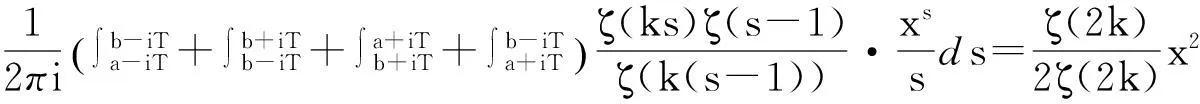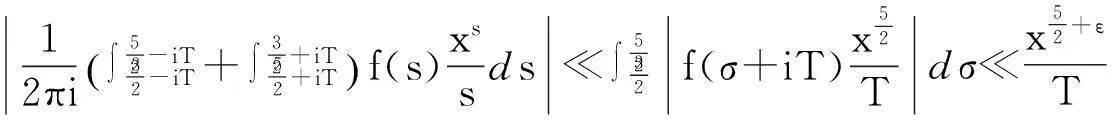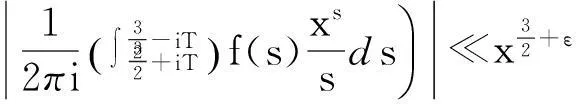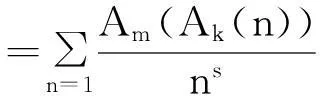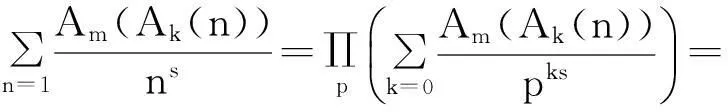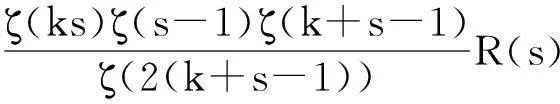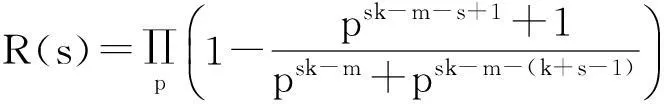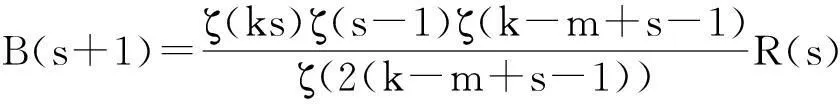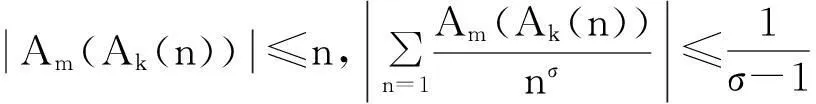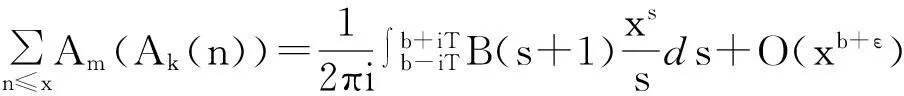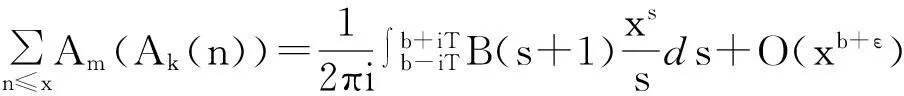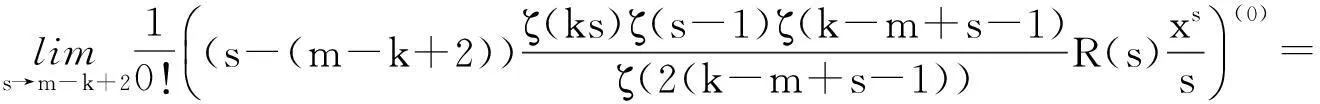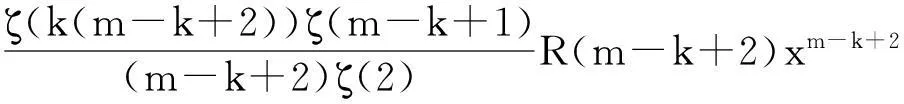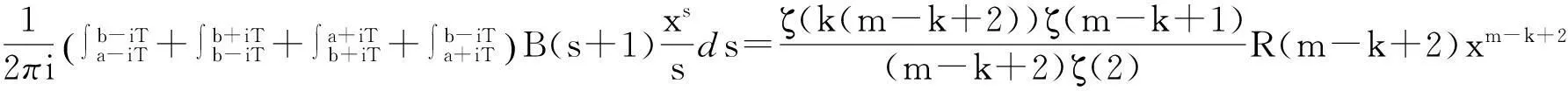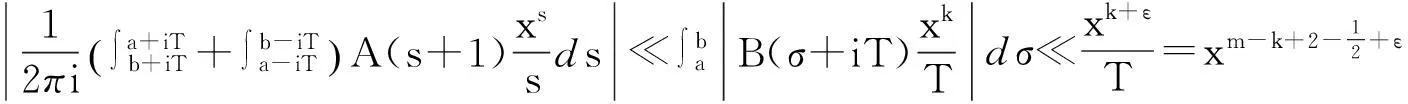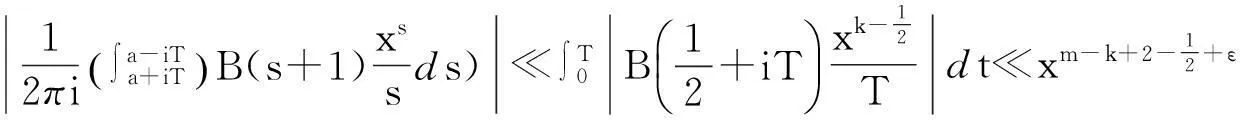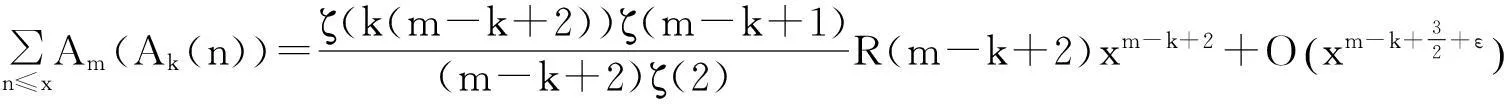关于混合补数数列的均值研究

陈珠社,黄　炜

(宝鸡职业技术学院 基础部,陕西 宝鸡　721013)



关于混合补数数列的均值研究

陈珠社,黄炜

(宝鸡职业技术学院 基础部,陕西 宝鸡721013)

摘要设n为任意正整数,Ak(n)为n的k次幂补数。利用初等数论和解析方法研究k次补数Ak(n)函数与m次补数Am(n)函数复合函数Am(Ak(n))的复合均值问题,给出两个有趣的渐近公式。

关键词k次幂补数;混合补数;均值;渐近公式

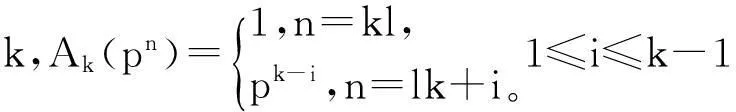
显然Ak(n)=nk-i≤nk,例如k=2时,有

A2(1)=1,A2(2)=2,A2(3)=3,A2(4)=1,A2(5)=5,A2(6)=6,A2(7)=7,A2(8)=2,…,

即

Ak(2)=2k-1,Ak(3)=3k-1,Ak(2k)=1,…,

当k=2或k=3时称Ak(n)为n的平方幂或者立方幂补数,记作A2(n)或A3(n) 。在文献[1]的第27个问题中,美籍罗马尼亚著名数论专家F.Smarandache教授建议研究有关n的k次补数Ak(n)的性质。目前,对于补数问题的研究文献很多[2-11],获得了不少有趣的结果,张文鹏[2]也研究了补数的性质,给出了几个有趣的恒等式,文献[3]中也对补数数列做了研究,给出了几个较强的渐近公式,文献[4]中研究了对于正整数k,m(3≤m

定理1设k≥2,m=k是两个给定的正整数,n为任意正整数,Ak(n)为n的k次补数,ζ(s)是Riemann-zeta-函数,对任意的实数x≥1,有渐近公式

其中:ε是任意给定的正整数。

定理2设k≥2,m>k是两个给定的正整数,n为任意正整数,Ak(n)为n的k次补数,ζ(s)是Riemann-zeta-函数,对任意的实数x≥1,有渐近公式

特别地,当k=2,m=3或k=2,m=4时有如下的推论。

推论1对任意的实数x≥1,有渐近公式

定理证明设s=σ+it,t为复常数,ζ(s)是Riemann-zeta-函数,p为素数,若k,m(k≥2,m>k),ε是任意正整数,当σ>k-1+ε时,定义

定理1的证明设p是一个素数,对于k次补数Ak(pn),有

(1)

其中:ε表示任意给定的正数。

即

(2)

我们可以容易地得到估计:

(3)

(4)

因此有

这就完成了定理1的证明。

定理2的证明设p是一个素数,对于k次补数Ak(pn)有

(5)

其中:ε表示任意给定的正数。

其中:ε表示任意给定的正数。

即

(6)

可以容易地得到估计:

(7)

(8)

结合式(7)、式(8),有

这就完成了定理2的证明。

参考文献:

[1]Smarandache F.Only Problems,Not Solutions[M].Chicago:Xiquan Publishing House,1993.

[2]Zhang Wenpeng.Identities On thek-th Power Complement[C]//Research on Smarandache Problems in Number Theory.Hexis,2004:61-64.

[3]Yao Weili.On thek-th Power Complement Sequence[C]//Research on Smarandache Problems in Number Theory.Hexis,2004:43-46.

[4]王婧哲.关于混合补数序列的均值性质[J].内蒙古师范大学学报:自然科学汉文版,2011,40(5):441-443.

[5]朱伟义.关于整数n的k次补数[J].数学学报,2005,48(4):817-820.

[6]张德瑜,翟文广.关于整数n的k次补数[J].山东大学学报:理学版,2006,41(5):4-6.

[7]李静.一个包含k次补数的方程[J].数学的实践与认识,2007,37(9):172-175.

[8]黄炜.K次方根序列的均值渐近公式[J].甘肃科学学报,2009,21(3):49-52.

[9]黄炜.关于Smarandache下部及上部阶乘数列[J].甘肃科学学报,2011,23(4):5-8.

[10]Tom M Apostol.Introduction to Analytic Number Theory[M].New York:Springer-Verlag,1976.

[11]张文鹏.初等数论[M].西安:陕西师范大学出版社,2007.

Study on Mean Value of Mix Complement Sequence

Chen Zhushe,Huang Wei

(DepartmentofBasis,BaojiVocationalandTechnicalCollege,Baoji721013,China)

AbstractLetnbe a positive integer,Ak(n) bek-power complement ofn.To study the question of compound mean values ofk-power complementAk(n) function andm-power complement compound functionAm(Ak(n)) ofAm(n) function,with the elementary number theory and analytic number theory and to give an interesting asymptotic formula.

Key wordsk-power complement;Mixed complement;Mean value;Asymptotic formula

中图分类号:O156.4

文献标志码:A

文章编号:1004-0366(2016)01-0021-04

作者简介:陈珠社(1964-),男,陕西武功人,硕士,副教授,研究方向为基础数学.E-mail:hwxy6@163.com.

基金项目:国家自然科学基金项目(10871123);陕西省自然科学基金项目(SJ08A28).

收稿日期:2015-02-02;修回日期:2015-05-11.

doi:10.16468/j.cnki.issn1004-0366.2016.01.005.

定义:设n为正整数,k次补数Ak(n)。

引用格式:Chen Zhushe,Huang Wei.Study on Mean Value of Mix Complement Sequence[J].Journal of Gansu Sciences,2016,28(1):21-24.[陈珠社,黄炜.关于混合补数数列的均值研究[J].甘肃科学学报,2016,28(1):21-24.]