水利工程中业主和监理博弈行为分析

王 洁，章恒全

（河海大学 商学院，江苏 南京 211100，E-mail：1174764572@qq.com）



水利工程中业主和监理博弈行为分析

王 洁，章恒全

（河海大学 商学院，江苏 南京 211100，E-mail：1174764572@qq.com）

摘 要：水利工程质量是决定工程建设成败的关键。为了应对施工过程中监理的道德风险问题，构建了业主与监理行为策略相互依赖的博弈模型，得出了不同参数关系下的纳什均衡解，解释了纯策略与混合策略的形成机理。分析了混合策略下，业主的奖励比例、对承包商的违规惩罚、对监理的合谋惩罚以及监理不合谋时其能力和态度决定的发现违规行为的概率与均衡策略的互动协调关系。并分析了重复博弈下业主采取报复策略对自身监督概率的影响，得到了监理获得最大期望时不同参数对业主监督概率的影响。

关键词：监督；合谋；纳什均衡；混合策略

水利工程往往规模大、过程复杂、建设期长，且建设地形复杂，需要专业的施工队伍进行施工。业主会选择专业的施工承包商，业主受限于专业知识的限制会委托专业的监理单位对施工承包商的施工过程进行监督，施工过程中的监理质量控制对保障水利工程质量起着至关重要的作用。但目前监理市场中高资质、高素质监理单位数量较少，据中国建设监理协会的研究报告，综合实力强、信誉度高的监理单位仅占10%，而实力弱、信誉存在缺陷的监理单位高达60%[1]。监理单位在监督过程中基于个体理性，追求自身利益最大化原则，存在道德风险问题[2]，有可能损害了业主的利益，影响水利工程的建设运行。

水利工程建设过程中业主与监理的交往实际是一场博弈，业主和监理通过信息交流与观察会选择最有利于自身利益最大化的策略[3]，最终形成博弈均衡解，因此适用博弈论对业主与监理的行为进行分析。国内外学者对此做了相应的研究。Abdul 等[4]通过分析合谋产生的原因，表明多层委托代理关系为工程合谋提供了条件，并建立了应对合谋的程序化模型。武英利等[5]在博弈论和寻租理论的基础上，分析了监理单位及业主之间的博弈关系，表明监理单位在施工阶段合谋的概率与业主监管的力度、积极性呈负相关。赵磊等[6]基于博弈分析，建立道德风险模型，表明业主根据惩处能力设计奖励与惩罚机制，可以最大限度地防止监理合谋行为的发生。王雪青等[7]构建了动态演化博弈模型，表明业主的动态惩罚策略能抑制策略的波动，并且使得业主倾向于完全监督。朱林美等[8]建立了一个基于监督成本与惩罚函数的关于工程监理的激励监督模型，得到了业主的最优监督水平和相应的激励策略。上述文献主要是从业主建立惩罚激励机制，满足监理的个人理性的角度，对双方的策略进行博弈分析，较多从业主角度出发，考虑业主行为对监理的影响，但对业主与监理单位之间决策的依赖性和行为诱导性的研究比较少，比如监理的合谋策略是一个道德风险问题，监理策略的选择依赖于业主的监督水平，同样业主的监督策略是一个逆向选择的问题，依赖于监理策略的选择。因此本文基于博弈论中的纳什均衡原理，分析水利施工过程中施工承包商发生违规行为时业主方与监理方的博弈，得到了业主与监理博弈的纳什均衡，针对其影响因素及内涵，得出了纯策略与混合策略的形成机制。最后将模型扩展到更具实际意义的重复博弈情形，分析在混合策略下，业主采取报复策略对自身均衡解影响的协调策略。

1 模型构建

1.1 模型假设

水利工程施工过程中，施工承包商为了追求自身的经济利益，会做出如偷工减料、欺骗业主等损害业主利益的行为，为此业主委托专业监理方来监督承包商的行为，但监理作为经济活动主体，追求自身利益最大化，可能会受到承包商的贿赂，与承包商合谋，因此业主在与监理单位的交往过程中实际进行着博弈。为了避免歧义，文中所指的业主和监理，均表示业主方和监理方，不考虑双方中存在的个人机会主义行为的影响。模型存在的基本假设如下：

假设1：业主和监理都是风险中性的，追求自身利益最大化。

假设2：策略空间集：业主为{监督，不监督}，监理为{合谋，不合谋}。

假设3：承包商在施工过程中违规，出现道德败坏行为；监理不合谋时，监理因能力水平及工作态度，以一定概率发现承包商的违规行为；业主监督时一定会发现承包商与监理的道德败坏行为。

假设4：按合同要求，业主的期望收益为B1，监理的期望收益为B2。承包商在出现道德败坏的违规行为时给业主带来的损失为ΔB。业主对承包商和监理的行为进行监督的成本为C，若监理合谋，监理会获得合谋报酬，为业主损失的一定比例αΔB，此时业主监督，对承包商和监理的惩罚分别F1、F2。若监理未合谋，业主未监督时，监理发现承包商违规行为的概率为γ，此时业主会对监理奖励对承包商惩罚收益的一定比例为βF1；业主进行监督，自己发现了承包商的违规行为并对其进行惩罚；业主监督的概率为x，监理不合谋的概率为y。

1.2 业主与监理的博弈模型

根据上述假设和各博弈方的行动策略，建立水利工程施工过程中业主与监理的博弈支付矩阵，如表1所示。

表1 业主与监理博弈支付矩阵

2 业主与监理的决策均衡分析

根据经济学原理，业主与监理作为“经济人”，业主不监督承包商及监理的行为会节省监督成本，监理通过与承包商合谋会得到合谋报酬，监理对业主监督概率的判断，在“诚信”与“投机”之间决策，而业主基于对监理的实力和信誉的判断，确定监督策略。当业主的行为对监理的预期收益没有影响，同时监理的行为对业主的预期没有影响时，该博弈存在唯一的Nash均衡解。

（1）无论业主采取何种策略，监理采取合谋与不合谋的预期收益相等，则：

求得业主采取监督策略的概率为：

由式（1）可知，均衡时业主监督的概率为：业主不监督时，监理合谋时获得的合谋报酬与不合谋并发现违规行为时获得的奖励收益之差，与业主监督时监理的惩罚与业主不监督时监理发现违规行为获得的奖励收益之差的比值。

（2）无论监理采取何种策略，业主监督与不监督的预期收益相等，则：

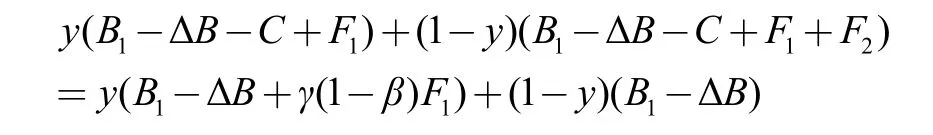
求得监理采取不合谋策略的概率为：

由式（2）可知，均衡时监理不合谋的概率为：监理合谋时业主监督获得的惩罚收益与监督成本之差，与监理合谋时业主获得的惩罚收益与监理不合谋并发现违规行为时业主对其奖励之差的比值。

因此，当业主监督的概率为x*，监理不合谋的概率为y*时，该博弈模型存在唯一的Nash均衡解。

根据式（1）、式（2）的存在条件，分析纳什均衡解在不同的参数条件下的变化情况：

当αΔ B＜ γβF1时，即监理合谋从承包商处获得的合谋报酬小于业主不监督时监理不合谋并发现违规行为从业主处获得的奖励，业主监督的概率x=0，此时若F1+F2＜C，即业主在监理合谋监督所获得的惩罚收益小于其监督的成本时，监理不合谋的概率y=0；否则监理不合谋的概率y=1。

若αΔB＞F2，即监理合谋获得的合谋报酬大于被发现业主对其的惩罚损失，业主监督的概率x=1，此时若C＜[1-γ(1-β)]F1，即业主的监督成本小于监理不合谋并发现违规行为时业主所需要支付的奖励，则监理不合谋的概率y=1，否则y=0。

若F1+F2＜C ，监理不合谋的概率y=0，此时若γβF1＜αΔB ＜F2，即监理合谋从承包商处获得的合谋报酬大于业主不监督时监理不合谋并发现违规行为从业主处获得的奖励，小于合谋被发现而被惩罚所支付的损失，则业主监督的概率x=0；

若C＜[1-γ(1-β)]F1，则监理不合谋的概率y=1，此时若γβF1＜αΔB＜F2，则业主监督的概率x=1。

当γβF1＜αΔB ＜F2且[1-γ(1-β)]F1＜C ＜F1+F2时，双方采取纳什均衡混合策略。将上述情况汇总成表，如表2所示。

表2 纳什均衡解的情况

3 混合策略均衡解的分析及协调机制

3.1 混合策略均衡解与奖励比例、惩罚的互动关系

根据上述分析，不难发现影响业主与监理行为的关键因素是业主对监理的奖励比例β、业主对承包商及监理的惩罚F1、F2以及监理不合谋时其能力和态度所决定的发现违规行为的概率γ，因此分析这些影响因素对混合策略均衡解变化的影响，即对业主监督概率x*和监理不合谋的概率为y*的变化趋势的影响，以及均衡解变化的图像。

（1）业主对监理的奖励比例β对于混合策略均衡解变化的影响。

对x*和y*分别关于β求导，得到

可以看出，在混合策略下业主监督的概率随着对监理奖励比例的增大而减小，监理不合谋的概率随着奖励比例的增加而提高。

对式（3）、式（4）变形，分别得到关于x*和y*的函数，则可以变为：

图1 x*与，y*与的图像

从图1可以看出，在0≤x*≤1范围内，业主监督的概率与业主监督的概率关于奖励比例的变化率呈二次函数关系，并且随着监督概率的不断增大过程中，业主监督的概率关于奖励比例的变化率不断地增大，并且增大的幅度不断减小；同理，在0≤y*≤1范围内，监理不合谋的概率关于奖励比例的变化率随着监理不合谋的概率的增大而增大的越显著。

（2）业主对承包商违规的惩罚F1对混合策略均衡解变化的影响。

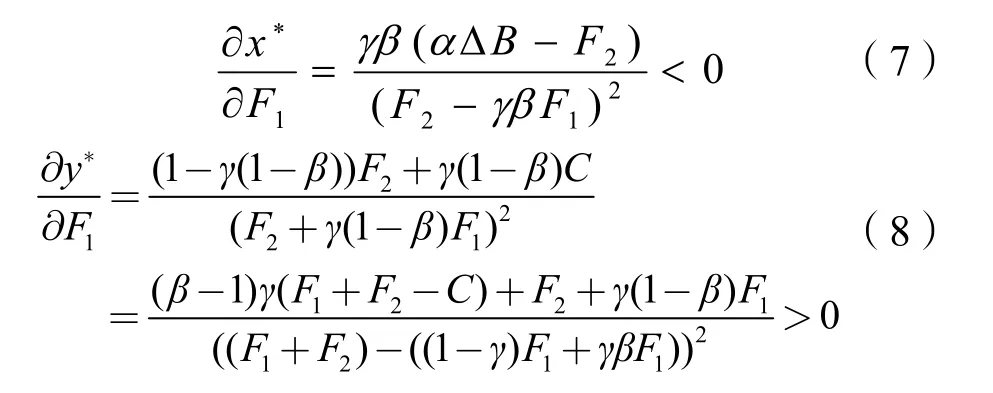
可以看出，在混合策略下业主监督的概率随着对承包商惩罚的增大而减小，监理不合谋的概率随着对承包商惩罚的增加而提高。

对式（7）、式（8）变形，可以得到：

因此，业主的监督概率x*与，监理不合谋的概率y*与的关系曲线如图2所示。

图2 x*与，y*与的图像

从图2可以看出，在0≤x*≤1范围内，业主监督的概率关于对承包商惩罚的变化率随着监督概率增大而增大，增大的幅度不断减小；同理，在0 ≤y*≤1范围内，监理不合谋的概率关于对承包商违规惩罚的变化率随着监理不合谋的概率的增大而先增大后减小，并且增大的幅度不断减弱，减小的幅度不断加强。

（3）业主对监理合谋的惩罚F2对混合策略均衡解变化的影响。

可以看出，在混合策略下业主监督的概率随着对监理合谋惩罚的增大而减小，监理不合谋的概率随着合谋惩罚的增加而提高。

对式（11）、式（12）变形，可以得到：

由此，业主的监督概率x*与，监理不合谋的概率y*与关系曲线如图3所示。

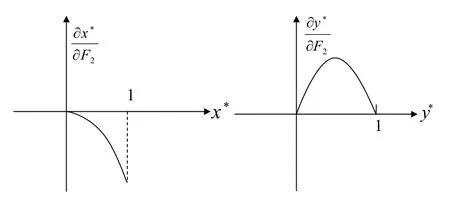
图3 x*与，y*与的图像

从图3可以看出，在0≤x*≤1范围内，业主监督的概率关于合谋惩罚的变化率随着监督概率增大而减小的越显著；同理，在0≤y*≤1范围内，监理不合谋的概率关于合谋惩罚的变化率随着监理不合谋的概率的增大而先增大后减小，并且增大的幅度不断减弱，减小的幅度不断加强。

（4）监理发现违规行为的概率γ对混合策略均衡解变化的影响。

可以看出，在混合策略下业主监督的概率随着监理发现承包商违规行为概率的增大而减小，监理不合谋的概率随着监理发现违规行为概率的增加而降低。

对式（15）、式（16）变形，分别得到关于x*和y*的函数，则可以变为：

因此，业主的监督概率x*与，监理不合谋的概率y*与的关系曲线如图4所示。

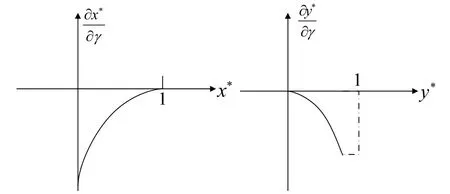
图4 x*与，y*与的图像

从图4可以看出，在0≤x*≤1范围内，业主监督的概率与业主监督的概率关于监理发现违规行为的概率的变化率呈二次函数关系，并且随着监督概率的不断增大过程中，业主监督的概率关于监理发现违规行为的概率的变化率不断地增大，并且增大的幅度不断减小；同理，在0≤y*≤1范围内，监理不合谋的概率关于监理发现违规行为的概率的变化率随着监理不合谋的概率的增大而减小的越显著。

3.2 重复博弈情形下业主策略的分析

将模型扩展到更具有实际意义的重复博弈模型，存在如下假设：

假设1：博弈能够无限次的进行，虽然在项目过程中博弈次数是有限的，但是从整个市场上看，博弈在未来的项目中还在继续，永远持续下去，因此可以将此博弈看成是无限的。此外，无限次重复博弈去掉某一阶段前的所有阶段，仍为无限次重复博弈，因此本文将第t-1阶段作为该无限次重复博弈的第一阶段，所得结果与原博弈相同[9]。

假设2：在重复博弈中业主的期望收益不变，只观察混合策略下各参数对监理策略选择的影响。

假设3：业主一旦发现监理采取了合谋策略，那么业主就会对监理进行报复，终止与监理的合作。贴现率为δ，在第t阶段，若前t-1均未发现监理有合谋行为，则继续合作，否则业主报复监理，终止合作[10]。

（1）监理不合谋时，监理的收益现值为：

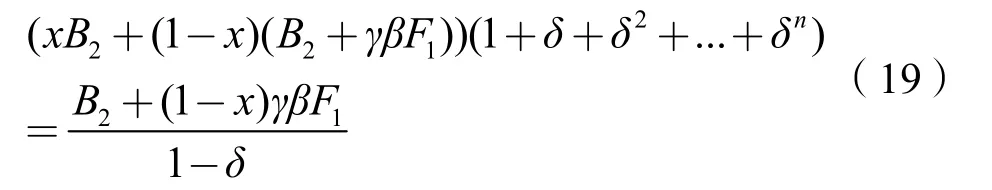
（2）监理合谋时，监理的收益现值为：

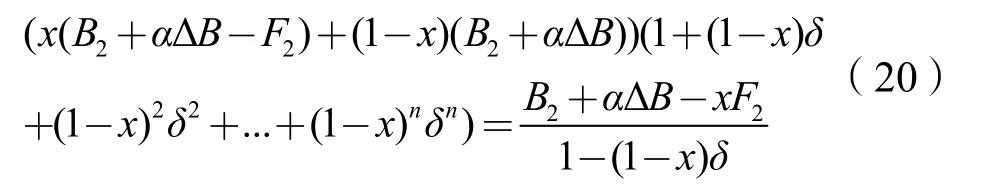
对监理的总期望收益求导，令：

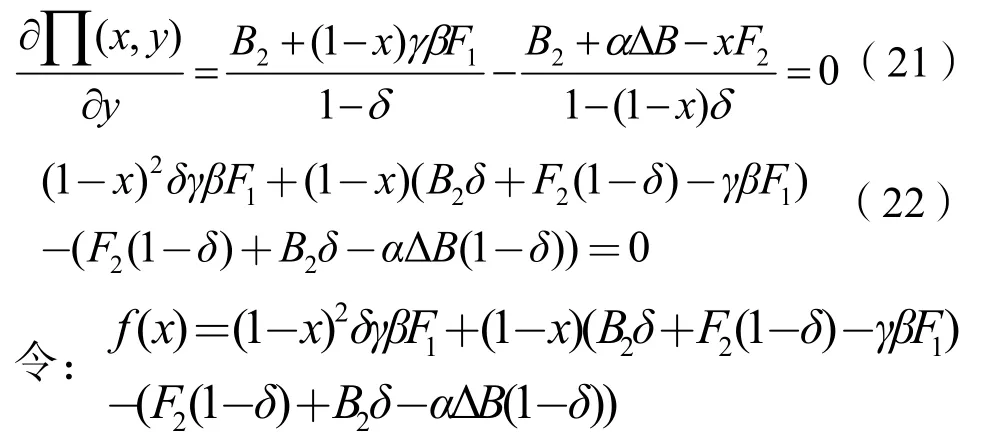
可以看出f(x)在0≤x≤1是关于x二次函数，f(0)=(1-δ)(αΔB-γβF1)＞0，f(1)=(αΔB-F2)(1-δ)-B2δ＜0，对称轴为，所以f(x)关于x的图像如图5所示。

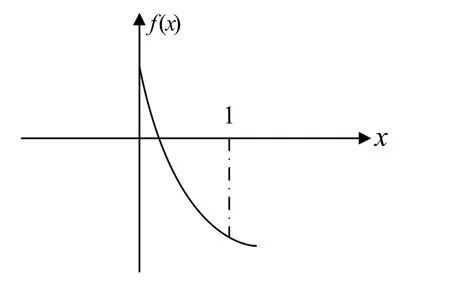
图5 f(x)关于x的图像

从图5可以看出，存在业主以一定概率监督时，监理可以取得最大期望，并且业主监督概率随参数变化而变化，现对业主监督概率随参数的变化情况进行分析。

（1）对式（22）求x关于贴现率δ的变化情况，可以得到：

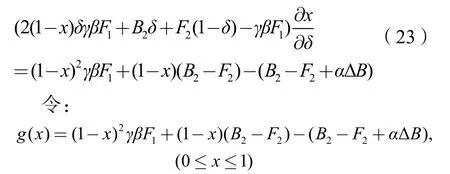
图6 g(x)关于x的图像

根据图6，g(x)在0≤x≤1恒小于0，同时，2(1-x)δγβF1+B2δ+F2(1-δ)-γβF1＞0代入式（23）求得，即监理获得最大期望时，随着贴现率的提高，业主监督的概率不断地减小。

（2）观察式（22）可以发现，x关于奖励比例β、对承包商惩罚F1、监理发现违规行为γ的变化情况相同，因此只分析x关于奖励比例β的变化情况，其余两种情况与其相同。

对式（22）求x关于奖励比例β的变化情况，可以得到：

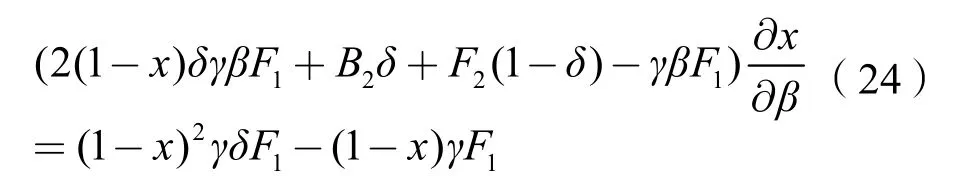
令h(x)=(1-x)2γδF1-(1-x)γF1,(0≤x≤1)，则h(0)=γ( δ-1) F1＜0；h ( 1 ) = 0，且对称轴为，当；当，h(x)关于x的图像如图7所示。

图7 h(x)关于x的图像

同理可得，随着业主对建立的承包商惩罚的不断增加和随着监理能力的不断提升及态度的不断端正，在不合谋时发现违规行为的概率的不断提高，业主监督的概率不断地减小。

（3）对式（22）求x关于对监理合谋惩罚F2的变化情况，可以得到：

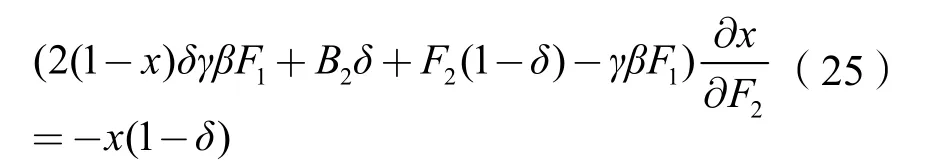
因此在重复博弈模型中，监理可以获得最大期望值，并且贴现率越高、对监理的奖励比例越大、对承包商违规惩罚越重、对监理的合谋惩罚越重，监理在不合谋时发现违规行为的概率越高，业主监督的概率越低。

4 结语

本文构建了水利工程施工过程中业主与监理行为相互依赖的博弈模型。首先，建立了双方静态博弈模型，并找到了不同参数条件下的博弈纳什均衡解；其次，针对纳什均衡解中的混合策略情形，分析了业主对监理的奖励比例、业主对承包商的违规惩罚、对监理的合谋惩罚和监理发现违规行为的概率对均衡解的影响机理，表明通过调整参数可以得到自身的最佳策略。并将模型延伸到更具实际意义的重复博弈模型，讨论了业主采取报复策略时均衡解的影响因素及变化情况，得到在业主以一定概率监督时监理可以取得最大期望收益，并且通过增大贴现率、提高对监理的奖励、增大对承包商及监理不德行为的惩罚和增大监理对违规行为的发现概率，可以使得业主的策略向不监督转化。本文从另一个角度分析了业主方和监理方博弈行为，可以看出双方策略存在的依赖性及诱导性，并且通过对均衡解变化的分析以及对重复博弈情形的考虑，使得结果更加具有实际意义，为水利工程中业主和监理的交往提供了依据。

参考文献：

[1] 段清谊．水利工程施工监理质量控制信息系统[D]．黑龙江大学，2013．

[2] Paul Anthony Bowen，Akintola Akintoye，Robert Pearl，Peter J．Edwards．Ethical Behavior in the South African Construction Industry[J]．Construction Management and Economics，2007，25：631-648．

[3] 郑君君，张 平，胡小诗，蒋伟良．基于随机微分方程的股权拍卖保价策略及模型研究[J]．系统工程理论与实践，2013，33（4）：893-900．

[4] Abdul Rahman H，Wang C，Saimon M A．Client’s Perspectives of Professional Ethics for Civil Engineers[J]．Journal of South African Institution of Civil Engineering，2011，53（2）：2-6．

[5] 武英利，彭 丰．承包商在工程建设各阶段的寻租博弈[J]．武汉大学学报（工学版），2013，46（6）：780-783．

[6] 赵 磊，钟 胜．工程建设中的施工与监理串谋分析[J]．西南交通大学学报，2013，48（6）：1136-1141．

[7] 王雪青，朱丽娜，杨秋波．建筑市场监理过程中失信行为的演化博弈分析[J]．广西大学学报（自然科学版），2013，38（1）：202-207．

[8] 朱林美，周 晶，吴孝灵．基于委托代理的工程监理激励—监督模型[J]．运筹与管理，2011，20（3）：176-180．

[9] 李 杨．非经营性政府投资项目参建主体博弈模型研究[D]．华北电力大学，2014．

[10] 谢识予．经济博弈论[M]．复旦大学出版社，2002．

王 洁（1990-），女，硕士研究生，研究方向：管理科学与工程；

章恒全（1957-），男，教授，博士生导师，研究方向：工程项目管理，投资管理。

Behavior Game Analysis of Owners and Supervisors in Water Conservancy Projects

WANG Jie，ZHANG Heng-quan
（School of Commercial，Hohai University，Nanjing 211100，China，E-mail：1174764572@qq.com）

Abstract：Quality is key to success of hydraulic engineering projects. In order to reduce moral risks of the supervisors in the construction process，a game model is established between owners and supervisors. The Nash equilibrium solution is obtained in the different parameters and the mechanism of the pure strategy and mixed strategy equilibrium is explained. Secondly，it analyzes interactive coordination relationship between mixed strategy equilibrium solution and parameters of the owners' incentive ratio，the punishment of contractors' violation and supervising agent’s collusion and the probability of finding irregularities determined by supervising agent’s ability and attitude when not in collusion. At the end of the analysis，in repeated game the influence of the owner's retaliation strategy on the self-supervision probability is analyzed，and the influence of different parameters to the owner's supervision probability is obtained when the supervisor achieves maximum expectation.

Keywords：supervision；collusion；Nash equilibrium；hybrid strategy

作者简介：

收稿日期：2015-12-02．

中图分类号：TU712.2

文献标识码：A

文章编号：1674-8859（2016）01-071-06

DOI:10.13991/j.cnki.jem.2016.01.013