XLPE电缆局放信号传播特性仿真研究

汪迪锋，孔海洋，吴 磊,李文娟

(1.广东电网有限责任公司江门供电局，广东 江门 529300；2.武汉大学电气工程学院，湖北 武汉 430072；3.中国长江电力股份有限公司溪洛渡水力发电厂，云南 昭通 657300)

0 引言

局部放电通常是引起电缆及其附件绝缘性能下降的主要原因之一，对电缆局部放电信号的在线监测技术及其定位技术成为近年来国内外专家学者的研究热点[1-4]。然而，局放信号在电缆介质中传播出现严重的衰减和耗散，使得接收到的信号并不是真实的局部放电信号。因此，研究电缆中局放信号的传播特性，掌握局放信号在电缆中的传播规律，是将局放信号从噪声和外界干扰信号中识别、提取出来的关键，也是确定局部产生位置及其严重程度的前提，其研究结果将有利于提高局部放电量定量和局部放电定位的精度。

局放信号是一种脉冲电流，关于局部放电信号在同轴电缆中的传播，已经可以通过经典的行波理论列出波动方程从而解出能够表征电缆特性的特性阻抗及传播常数。文献[5]指出局部放电信号在电缆中传播，其衰减的倍率随信号频率和传播距离的增加将产生严重的衰减。文献[6]通过对长度不等的11 kV电缆进行局部放电信号传播的仿真实验，结果表明输出脉冲信号的脉冲上升时间和脉冲宽度将随局部放电信号在电缆中传播距离的增加而单调上升。由于电缆及其附件的结构复杂，仍然无法将局部放电信号在电缆中的传播过程用精确的数学表达式来量化表示[7-9]。

为了电力电缆的局放在线监测能够实现局放放电量的定量和局放定位，必须掌握局放信号在电缆中传播的规律与特征。本文使用现有的电缆分布参数数值模型进行局放信号在电缆中传播特性的数值仿真计算，以实际电力电缆的参数进行了仿真计算，最终的计算结果可以为局放信号分析程序提供参考，从而提高局放放电量和局放定位的精度。

1 模型建立

1.1 电缆模型

在电缆结构中，交联聚乙烯电力电缆的内半导电层，除了在线芯和主绝缘之间起着平滑电场的作用外，还对局放信号中的高频分量有着很严重的衰减和散射作用，从而增加了检测局放信号的难度。因此，本文采用Bergeron Model单芯电缆模型来仿真局放信号在电缆中的传播，Bergeron Model将电力电缆简化为外皮、绝缘层和导体层3个部分，如图1所示。图中外皮主要起到屏蔽和保护的作用。

图1 Bergeron模型Fig.1 Bergeron model

MATLAB的电力系统模块库中分布参数等值电路在电力电缆长度不大于300 km时，能够代替电力电缆分布参数电路，这样不仅很好地近似了分布参数型的电路，同时也简化了电路模型，有利于分析计算，电缆参数计算如下式[10-12]。

式中：R0、L0、C0、G0分别为电缆单位长度上的电阻、电感、电容和电导；DA为电缆屏蔽层直径（即外径）、DC为电缆线芯直径（即内径）；ε为材料相对介电常数；ε0为真空介电常数；μ0为磁导率；Li、Le分别为内部电感和外部电感ρ为导线材料的电阻率；S为导线的标称截面积。

1.2 局放信号的数学模型

局放信号是一种具有陡峭上升沿、包含多种高频率分量的窄脉冲信号。高频分量主要集中的频率范围为1 kHz～100 MHz，并且频率越高，其在电力电缆中传播时的衰减将会越严重[13]。随着电力线上负载增加和传输距离的增加，传输的准确率随之下降。因此，建立有效的局放信号的数学模型有利于更清楚地了解和分析电缆中局放信号的传播特性。常见的模拟局放信号的数学模型主要有单指数衰减模型、双指数衰减模型、单指数衰减振荡模型和双指数衰减振荡模型。在这四种局放的数学模型中，通常用双指数衰减模型来模拟局放信号，其数学表达式为

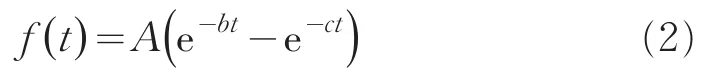
本文双指数衰减函数的数学模型参数为A=0.012 5，b=4×106，c=494×106，脉冲信号波形图如图2所示，该脉冲信号的幅值为9.688×10-4V，上升时间大约为128 ns，脉冲宽度约为550 ns，出现幅值时间为 2.24×10-7。

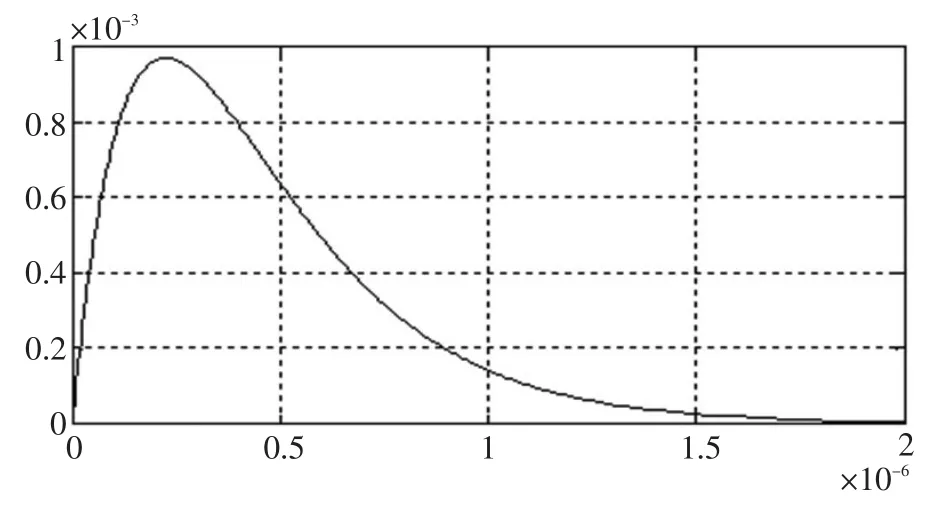
图2 局放信号的双指数衰减模型Fig.2 Double exponential attenuation model of PD

2 仿真分析及结果

基于Simulink搭建仿真电路，如图3所示。将局放信号从电缆的一端A点注入，观察从电缆另一端B点出来的信号波形并将其与原始信号波形进行对比分析。

通过改变电缆长度、电缆参数、脉冲信号的上升时间以及脉冲信号的频率进行四组不同的仿真，对比分析研究电缆中局放信号的传播特征，具体如下。

图3 局放信号在电缆中传播仿真电路图Fig.3 The simulation circuit of PD transmission in the cable

2.1 不同长度电缆的局放信号传播特性

配置3根长度分别为150 m、500 m和1 000 m的电缆。将上述上升时间为128 ns的局放信号分别加载在3根电缆上，得到局放信号分别经过3根电缆后的波形，仿真结果如图4所示。

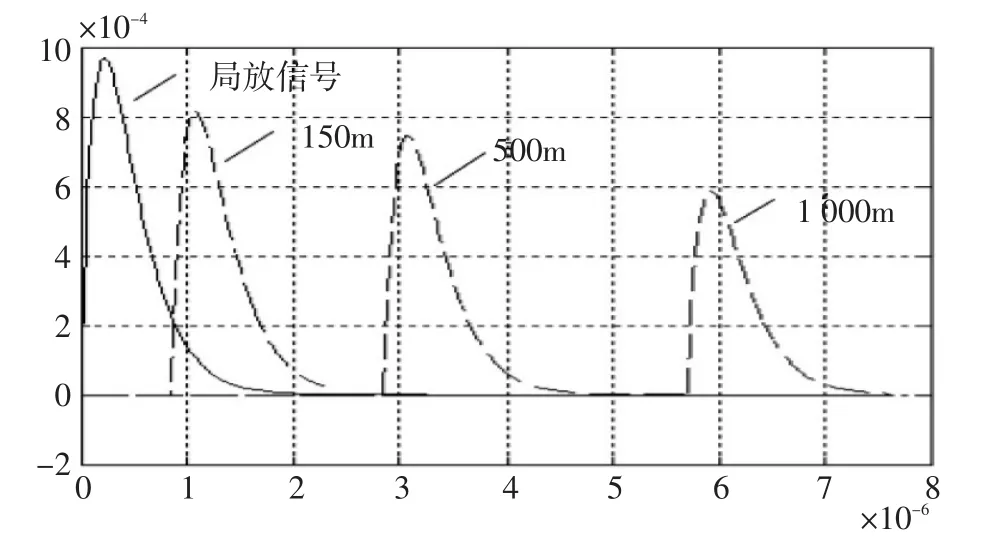
图4 局放信号在不同长度电缆中传播后的波形Fig.4 The PD waveforms after transmission in different length of cable

a)长度为150 m的电缆

经过电缆后的局放信号存在一个时间上的延时以及幅值的衰减，衰减后的局放信号的峰值变为8.159×10-4V，出现峰值的时间为1.079×10-6s，脉冲时延为854.83 ns。而脉冲的上升时间与脉冲宽度几乎没有变化，分别为129 ns和557 ns，其原因主要是本实验中忽略了半导电层的衰减和散射作用及电晕效应等因素的影响。

b)长度为500 m的电缆

原始局放信号经过500 m的电缆后，其峰值为7.489×10-4V，出现峰值的时间为3.074×10-6s，产生的时延为2 849.4 ns。上升时间和脉冲宽度分别为129 ns和552 ns，与原始信号的上升时间和脉冲宽度没有太大的区别。

c)长度为1 000 m的电缆

原始局放信号经过1 000 m的电缆后产生了更为明显的衰减。其峰值变为5.882×10-4V，出现峰值的时间变为5.923×10-6s，产生的时延为5 698.9 ns。上升时间和脉冲宽度分别为129 ns和553 ns，与原始信号的上升时间和脉冲宽度没有太大的区别。

由此，局放信号在电缆中传播后幅值会出现一定的衰减，并且在时间上有延迟。同时随着电缆长度的增加，幅值的衰减更为严重，延迟的时间也越来越长。

2.2 不同电压等级电缆的局放信号传播特性

取电缆的长度为500 m，选取6/10 kV、26/35 kV和64/110 kV 3个不同电压等级的电力电缆来进行仿真分析，得到局放信号分别经过3根电缆后的波形，仿真结果如图5所示。

a)6/10 kV电力电缆。

通过6/10 kV电力电缆后的信号峰值变为7.380×10-4V，上升时间为129 ns，脉冲宽度为552 ns，出现峰值时间为 3.279×10-6s(3 279 ns)，时延为3.0548×10-6s(3 054.8 ns)。产生了较为明显的衰减。

b)26/35 kv电力电缆。

原始局放信号通过该电压等级的电缆后，峰值变为7.489×10-4V，上升时间为129 ns，脉冲宽度为552 ns。出现峰值的时间为3 074 ns，时延为2 849.4 ns。从数据看出其衰减程度略有减小。

c）64/110 kV电力电缆。

原始局放信号通过该电压等级的电缆后，信号峰值变为7.482×10-4V，上升时间为128 ns，脉冲宽度为552 ns，出现峰值的时间变为2 956 ns，时延为2 732.3 ns。

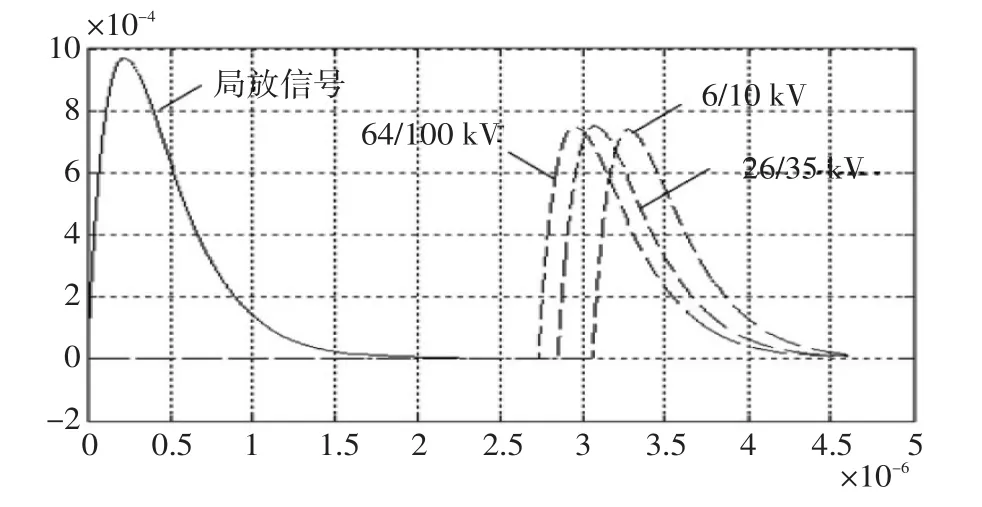
图5 局放信号在不同电压等级电缆中传播后的波形Fig.5 The PD waveforms after transmission in different voltage level cable

局放在不同电压等级的电缆中传播时幅值的衰减几乎相同，即在仿真中电缆参数对信号幅值衰减的影响很小；同时，信号在较高电压等级电缆中的时延小于在较小电压等级电缆中的时延。

2.3 宽脉冲与窄脉冲在电缆中传播特性

取电缆的长度为500 m，电压等级为26/35 kV。宽脉冲信号即为图2中双指数衰减脉冲，其脉冲宽度约为550 ns，该信号通过电缆后的幅值变为7.489×10-4V，上升时间为129 ns，脉冲宽度552 ns，出现幅值时间 3.074×10-6s，时延为2849.4ns。窄脉冲信号的波形幅值为9.688×10-4V，上升时间为38 ns，脉冲宽度206 ns，比宽脉冲信号的上升沿陡峭了许多，出现幅值时间为68 ns。经过电缆后，信号幅值变为7.4839×10-4V，上升时间为38 ns，脉冲宽度为206 ns，出现幅值时间为2 917 ns，时延为2 849.4 ns。

将宽、窄脉冲通过电缆后的波形如图6所示。由图看出，峰值相等的宽脉冲信号与窄脉冲信号，除了本身在上升时间和脉冲宽度上的区别，它们通过相同的电力电缆后脉冲幅值的衰减与产生的时延完全相同。

图6 宽脉冲信号与窄脉冲信号的比较Fig.6 The comparison of wide pulse signal and narrow pulse signal

2.4 正弦衰减信号在电缆中的传播特性

取电缆的长度为500 m，电压等级为26/35 kV。仿真生成3个频率分别为10、30、50 MHz的正弦衰减信号来比较不同频率的正弦衰减信号在电缆中的传播特征，正弦衰减信号波形如图7所示。选取各波形的峰值及其出现时刻进行分析，不同频率的正弦衰减信号峰值及经过电缆后的信号峰值如表1、2所示。

图7 正弦衰减信号波形Fig.7 The waveform of sine attenuation signal

表1 原信号的波形峰值表Tab.1 The peak value of original signals

10MHz信号各个峰值衰减比例依次为：23.61%，22.64%，21.74%，22.77%，22.75%，22.74%。各个峰值之间的时间间隔为0.5T=50 ns。各峰值经过电缆后的时延均约为2 849.4 ns。

表2 经过电缆后信号的波形峰值表Tab.2 The peak value of signals after transmission

30 MHz信号各个幅值衰减比例依次为：28.57%，26.76%，26.03%。26.56%，26.92%，27.5%，26.67%，27.27%，25%，29.79%。各幅值出现间隔大约为16 ns。各峰值的时延几乎都约为2 849.4 ns。50 MHz信号各个峰值衰减比例依次为：32.14%，31.58%，32.39%，33.33%，31.94%，32.84%，32.20%，32.69%，33.33%，34.21%。各峰值出现的时延都约为2 849.4 ns。

综上所述，频率为10、30和50 MHz的正弦衰减信号在同一电缆中传播后信号幅值的衰减分别为22%、27.5%和33%，说明在同一电缆中，频率越高的信号其幅值衰减越大。由于仿真在同一电缆中进行，因此各个频率信号出现的时延都相同。

3 结论

通过四组不同的仿真实验，得到以下结论：

1)局放信号在电缆中传播后幅值会出现一定的衰减，并且在时间上有一个延迟。同时随着电缆长度的增加，幅值的衰减更为严重，延迟的时间也越来越长；

2)信号在不同电压等级的电缆中传播时幅值的衰减几乎相同，即在本实验中电缆参数对信号幅值衰减的影响很小；同时，信号在较高电压等级电缆中的时延小于在较小电压等级电缆中的时延；

3)对于峰值相等的宽脉冲信号与窄脉冲信号，除了本身在上升时间和脉冲宽度上的区别，二者通过相同的电力电缆后脉冲幅值的衰减与产生的时延是完全相同的；

4)在同一电缆中，频率越高的信号其幅值衰减也越大。

（References）

[1]魏钢，唐炬，文习山，等.局部放电信号在交联聚乙烯高压电力电缆中的衰变及其检测[J].高电压技术，2001，37(6)：1377-1383.Wei Gang,Tang Ju,Wen Xishan,et al.Decay and detection of partial discharge signals in high-voltage cross-linked polyethylene power cable[J].High Voltage Engineering,2001,37(6):1377-1383.

[2]徐红义，黄斌，郭和清.XLPE高压电缆在线监测方法综述与设计[J].湖北电力，2009，33(6)：38-40.Xu Hongyi,Huang Bin,Guo Heqing.Summary and design ofon-line monitoring method forXLPE high-voltage cable[J].Hubei Electric Power,2009,33(6):38-40.

[3]张磊祺，盛博杰，姜伟，等.基于电缆传递函数和信号上升时间的电力电缆局部放电在线定位方法[J].高电压技术，2015，41(4)：1204-1213.Zhang Leiqi,Sheng Bojie,Jiang Wei,et al.On-line powercable partialdischarge localisationmethod based on cable transferfunction and detected pulse rise-time[J].High Voltage Engineering,2015,41(4):1204-1213.

[4]郭灿新，张丽，钱勇，等.XLPE电力电缆中局部放电检测及定位技术的研究现状[J].高压电器，2009，45(3)：56-60.Guo Canxin,Zhang Li,Qian Yong,et al.Current sta⁃tus of partial discharge detection and location tech⁃niques in XLPE power cable[J].High Voltage Appa⁃ratus,2009,45(3):56-60.

[5]段乃欣，赵中原，邱毓昌，等.XLPE电缆中局部放电脉冲传播特性的实验研究[J].高压电器，2002，38(4)：16-18.Duan Naixin,Zhao Zhongyuan,Qiu Yuchang,et al.Experimental study on the propagation characteris⁃tics of the PD pulse in XLPE power cable[J].High Voltage Apparatus,38(4):16-18.

[6]Sheng Bojie,Zhou Chengke,Hepburn D M,et al.Partial discharge pulse propagation in power cable and partial discharge monitoring system[J].IEEE Transactions on Dielectrics and Electrical Insula⁃tion,2014,21(3):948-956.

[7]Yu Ting-Chung,Marti Jose R.A robust phase-coor⁃dinates frequency-dependent underground cable model(zCable)for the EMTP[J].IEEE Transactions on Power Delivery,2003,18(1):189-194.

[8]Jobava R,Pommerenke D,Heinrich R,et al.Calcu⁃lation of pulse propagation in coaxial cables with multi-layered insulation system[J].DIPED-2000 Pro⁃ceedings,2000:35-40.

[9]Yu T C.zCable model for frequency dependent mod⁃elling of cable transmission systems[J].IPST,2001:1034-1040.

[10]Oussalah N,Zebboudj Y,Bogg S A.Partial dis⁃charge pulse propagation in shielded power cable and implications for detection sensitivity[J].IEEE Electrical Insulation Magazine,2007,23(6):5-10.

[11]陈锡阳，桂峻峰，高胜友，等.局部放电信号在电缆中的传播对波形影响的分析[J].电线电缆，2014(4)：37-39.Chen Xiyang,Gui Junfeng,Gao Shengyou,et al.Analysis of the impact to the waveform of partial discharge signalduring its propagation in cable[J].Electric Wire＆Cable,2014(4):37-39.

[12]张伟，张龙，黄志伟，等.考虑频变参数的交联聚乙烯电缆中局部放电传播特性的时域分析[J].高电压技术，2014，40(11)：61-67.Zhang Wei,Zhang Long,Huang Zhiwei,et al.Time domain analysis of partial discharge propagation in cross-linked polyethylene cables considering fre⁃quency-dependent parameters[J].High voltage engi⁃neering,2014,40(11):61-67.

[13]刘红，张东来，孙光伟.电力线载波中传输线模型的建立及应用[J].电力系统及其自动化学报，2002，14(3)：27-32.Liu Hong,Zhang Donglai,Sun Guangwei.The es⁃tablishment and application of transmission line model in power line carrier[J].Proceedings of the EPSA,2002,14(3):27-32.