基于多种群合作协同算法的电力系统调度优化

刘 勇， 伍大清, 2, 3, , 5， 孙 莉， 杨治平

(1. 四川省人工智能重点实验室， 四川 自贡 643000； 2. 南华大学 计算机科学与技术学院， 湖南 衡阳 421001；

3. 安徽大学 教育部计算智能与信号处理重点实验室， 安徽 合肥 230039； 4. 东华大学 旭日工商管理学院，

上海 200051； 5. 农业部农业信息服务技术重点实验室， 北京 100081)

基于多种群合作协同算法的电力系统调度优化

刘 勇1， 伍大清1, 2, 3, 4, 5， 孙 莉4， 杨治平4

(1. 四川省人工智能重点实验室， 四川 自贡 643000； 2. 南华大学 计算机科学与技术学院， 湖南 衡阳 421001；

3. 安徽大学 教育部计算智能与信号处理重点实验室， 安徽 合肥 230039； 4. 东华大学 旭日工商管理学院，

上海 200051； 5. 农业部农业信息服务技术重点实验室， 北京 100081)

为解决电力系统环境经济调度这一复杂多目标约束优化问题，提出一种有效多种群合作协同优化算法，采用多个种群对搜索空间进行搜索，运用新型的速度位移更新方式以及种群周期内拓扑结构重组策略. 结果表明，该算法能对解空间进行更加全面、充分的探索，可快速找到一组分布具有尽可能好的逼近性、宽广性和均匀性的最优解集合.将该算法应用到某电力系统的环境经济调度中, 其仿真计算结果与其他求解方法结果的对比分析表明, 该算法可以有效兼顾全局收敛性和Pareto非劣调度方案的多样性, 具有较高的效率以及鲁棒性.

合作协同优化； 多种群优化； 粒子群优化； 环境经济调度

近年来，随着人类对环境保护的日益重视，电力系统中传统的经济调度模式已不能满足环保的需求，一种综合考虑发电成本和污染气体排放的新型环境经济调度(environmental-economic dispatch， EED)模式受到国内外学者的广泛关注.国内外学者通过分析运用电力调度的约束模型，将电力调度的经济最小化作为单一目标进行优化，也有采用多目标遗传算法NSGA-Ⅱ[1]、粒子群优化算法[2]、进化规划算法[3]和差分进化算法[4]等来求解电力系统环境经济调度问题，并取得了丰富的研究成果，但这些方法仍存在诸如计算速度慢、搜索精度不高、难以处理实际工程问题中复杂的约束条件等问题.

本文以求解EED的多目标约束优化问题为背景,将多目标分解思想与人类社交行为有机地结合起来,提出一种有效的多种群合作协同微粒群优化算法(an effective co-evolutionary multi-swarm particle swarm optimization，简称ECMPSO).ECMPSO将多目标优化问题分解为若干个单目标优化子问题,每个子问题对应一个子种群，不同子种群间通过共享外部存档集相互合作,有效地近似整个Pareto前沿面，提出了基于人类奖惩行为的奖励-惩罚学习因子的微粒群优化算法速度更新方式.该算法的理论分析与试验结果表明,ECMPSO在收敛性和多样性方面均表现出明显优势，能够避免陷入局部最优解，可高效搜索外部存档中新粒子，能够获得均匀的Pareto前沿.

1 多目标环境经济调度问题的数学描述

电力系统环境经济调度问题是在已知机组开停计划的情况下，以某时间段机组的有功出力为决策变量，将系统总负荷合理分配，使整个机组消耗的燃料以及污染气体排放量达到最少化[5].

1.1 约束条件

(1) 发电机运行容量约束.每个机组的发电功率应介于其最小输出功率与最大输出功率之间，即

(1)

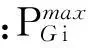
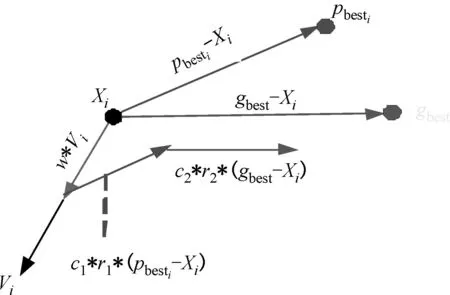
(2) 有功功率平衡约束.负载总的需求功率与网络损耗之和等于各机组发电功率之和，即

(2)

式中:Ploss为系统网络损耗；PD为系统总负荷需求；NG为系统内发电机总数.

采用B系数法，系统网损与发电机有功功率的关系为

(3)

式中：Bij， Bi0， B00称为B系数.

1.2 目标函数

(1) 燃料消耗目标函数为

(4)

式中：ai， bi， ci均为系统参数.

(2) 污染气体排放量函数为

式中：αi， βi， ξi， γi均为系统参数.

2 基于多种群合作协同的环境经济调度算法

2.1 算法原理

基本粒子群优化(PSO)算法[6]通常用来求解单目标优化问题，每个粒子视为搜索空间中待优化问题的可行解，假设n个粒子在D维的空间中，粒子之间通过相互竞争与协作来寻找问题的最优解，在每次迭代中，粒子个体搜索到的最好位置称为个体最优，用pbest表示，群体中所有粒子搜索到最好位置称为全局最优，用gbest表示，通常以寻找最低适应度值为最优.

在基本的PSO算法中，所有的粒子仅仅围绕个体最优和群体最优学习，显然,这是一个理想社会条件.然而,本文算法引进人的社交行为特点，而社交过程中环境因素给人带来巨大影响.粒子在搜索过程中也同样如此，不仅受到周围好环境(适应度值低的邻居粒子)的影响，也可能受到差环境(适应度值高的邻居粒子)的影响.但如果客观、理性看待这些“坏习惯/行为”，提前对这些“坏习惯/行为”的粒子有所警惕,采取措施，那么对搜索是非常有益的.因此,ECMPSO算法中引进最大局部邻居粒子Nmax,即每次迭代,每个小种群都会产生一个局部最优粒子，所对应的适应度值排序，最大的适应度粒子被选作Nmax, Nmax(t)=argmax{f(pbest1), f(pbest2), …, f(pbestn)}, f(·)代表每个粒子的适应度函数的评估值.ECMPSO引进一个随机学习因子r3,且r3服从标准正态N(0, 1)分布的随机数.每一代新个体的生成，判断是否对共享的外部存档集做出贡献决定r3的取值.如果产生的新个体能支配外部存档集中的非支配解，则产生r3>0的奖励学习因子，加快粒子的飞行速度，则有利于提高粒子勘测区域深度；如果产生的新个体未能支配外部存档集中的非支配解，则产生r3<0惩罚学习因子，将减缓粒子的飞行速度，有利于提高粒子开发广度.

基本PSO算法中，粒子在个体最优以及全局最优的引导下寻找区域的最优值，搜索过程如图1(a)所示，该搜索方式能促使粒子搜索速度加快，但很容易陷入局部最优解.ECMPSO算法的粒子搜索过程如图1(b)和1(c)所示，从图1(b)和1(c)能清楚看到，奖励学习项以及惩罚学习项能促使粒子探索更广阔的空间，有助于粒子跳出局部最优解，从而提高种群多样性，使其快速收敛到全局最优值.

ECMPSO算法中的子种群采用环形拓扑结构，为了粒子向周围环境中的不同的粒子学习，充分保持

(a) 基本PSO搜索过程

(b) ECMPSO奖励学习过程

(c) ECMPSO惩罚学习过程

Fig.1 Process of particles searching

2.2 数学描述

为了减少参数灵敏性对算法带来的影响，本文算法使用随机学习因子r1以及r2代替基本粒子群中的加速因子，每个粒子通过式(7)和(8)更新速度和位移.

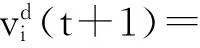
(6)

(7)

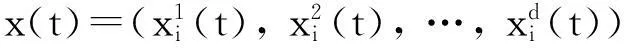
2.3 算法描述

ECMPSO算法基于多目标技术，种群中的粒子相互协同合作寻找到分布尽可能好的逼近性、宽广性和均匀性Pareto最优解集合.基于ECMPSO算法的环境经济发电调度流程如下：

步骤1 获得具有多台发电机组的电力系统中每台机组的出力数据上限与下限、燃料消耗函数的系数数据、有害气体排放量函数的系数数据、输电线路损耗的B系数数据和系统总负荷数据.

步骤2 建立电力系统环境经济调度问题的数学优化模型.

工作经验告诉我，面对幸福的选择困难情况时，相信自己的直觉，结果往往美滋滋。这一次，我毫不犹豫地选择GT，法拉利的GT跑车。

步骤3 初始化种群.随机初始化粒子数为N的群体以及对应的适应度, 针对多目标问题的目标个数N,将种群划分成N个子种群，各个粒子所对应的速度，最大迭代次数，粒子的局部最优位置pbest,群体最佳位置gbest以及每个子群体中Nmax,初始化外部存档集.

步骤4 迭代更新.对于每个种群的每个粒子进行如下操作：(1)对种群中所有的粒子采用式(6)和(7)更新粒子的速度和位置；(2)计算新粒子的各个目标适应度值,判断是否能支配外部存档中的非支配解，若是则产生奖励学习因子，若否则产生惩罚学习因子,分别更新pbest、gbest以及Nmax.注意, 这里对速度越界的粒子适应度值不进行更新.

步骤5 更新外部存档集，判断外部存档大小是否超过种群规模，若是，使用拥挤距离更新外部存档.

步骤6 迭代计数器累增1，是否能整除拓扑结构重组周期L.若是则执行步骤4;若否则执行步骤7.

步骤7 迭代次数累增,判断是否满足算法终止条件.若满足,则执行步骤8，否则转步骤4.

步骤8 输出Pareto最优前沿面, 算法结束.

步骤9 将确定的最终解作为指令，通过自动发电控制装置发送给相关发电厂或机组的自动控制调节装置,实现对机组发电功率的控制.

3 仿真试验结果与分析

3.1 测试函数

试验部分选用了国际测试函数ZDT系列的4个双目标问题来验证ECMPSO算法的有效性,这些测试问题能够在不同的方面对进化多目标问题进行测试.试验结果与NSGAII[1], MOABC[8], MOCLPSO[9]进行了对比.其中,NSGAII是一种公认而有效地进化多目标优化算法,MOABC是最近提出来的蜂群多目标优化方法, MOCLPSO是一种非常有效的微粒群多目标优化算法.表1列出了4个测试函数的表达式.

表1 测试函数

综合评价指标IGD(inverted generational distance)[10]被用来评估算法的性能.假定Q*为多目标优化问题理想PF上的一组均匀采样,Q为多目标优化算法求得的一组理想PF的逼近解,则解集Q的IGD指标定义如下

(8)

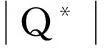
表2给出了4种算法在不同测试函数上的IGD度量结果，其中的数据为算法运行30次得到的平均值和方差.由表2可知，ECMPSO算法在ZDT1、 ZDT2、 ZDT3、 ZDT6收敛性和分布性上均优于其他3种算法，在ZDT3函数中MOCLPSO算法获得的IGD值与ECMPSO算法差不多，两者无显著差异.

表2 4种算法分别求得4个测试函数IGD评价指标

试验数据表明ECMPSO算法具有很强稳定性.图2中分别给出4种算法在ZDT1、 ZDT2测试函数上的Pareto前沿面.由图2表明，ECMPSO算法使用奖惩学习因子，种群周期内拓扑结构重组策略在解群分布的均匀性和宽广性方面要明显优于其他3种算法.

3.2 环境经济调度优化仿真试验

本试验用标准的IEEE 30节点六发电机测试系统,该系统的负荷需求为2.834 p.u，所有的线路通过41条输电线路进行连接.详细的燃料成本数据和氮氧化合物的排放系数见文献[11].为了清晰表明不同算法的性能，测试时考虑有网损和无网损两种

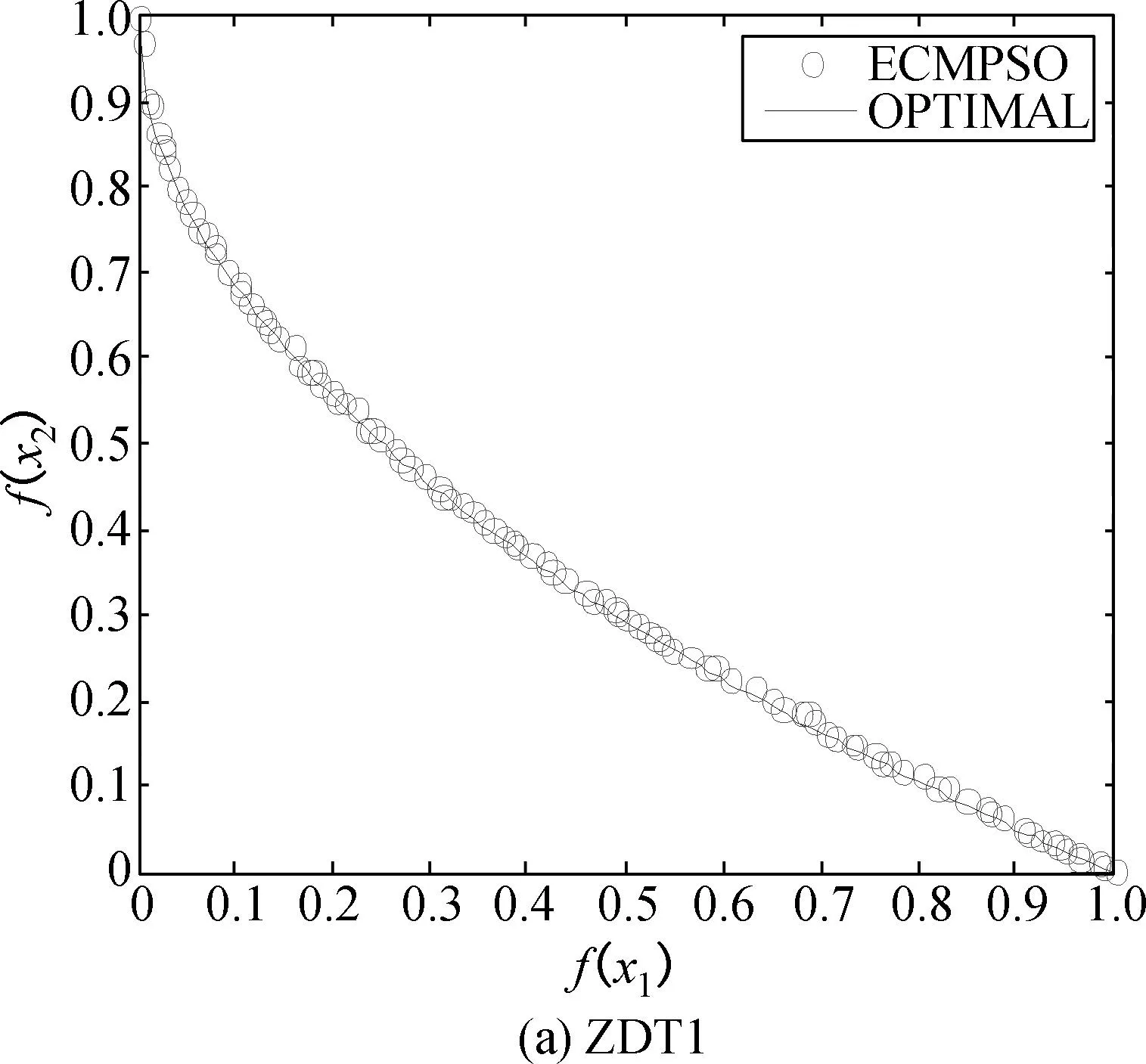
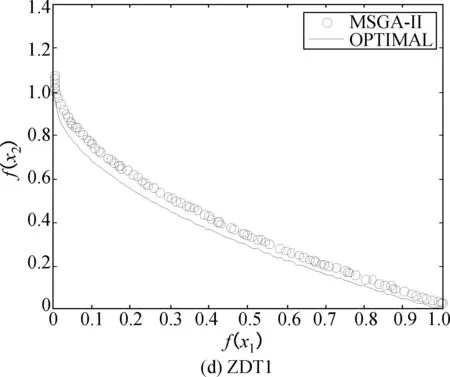
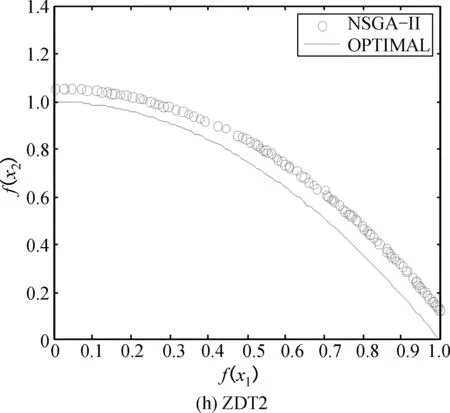
图2 各算法在2 000次迭代后的最优Pareto前沿面

情况.两种情况具体如下：

情况1 忽略6个机组的系统损耗，只考虑容量约束和平衡约束；

情况2 考虑系统损耗，同时考虑容量约束和平衡约束.

为验证本文算法的可靠性，在参数设置一致的情况下，每组试验独立运行20次，分别以最低的发电成本以及相应较好的排放、最低的排放量以及相应较低的发电成本两种方式来评估ECMPSO算法、DE-IMOPSO算法[12]、NSGAII算法[1]以及2LB-MOPSO算法.4种算法在情况1和2条件下的运算结果如表3～6所示.

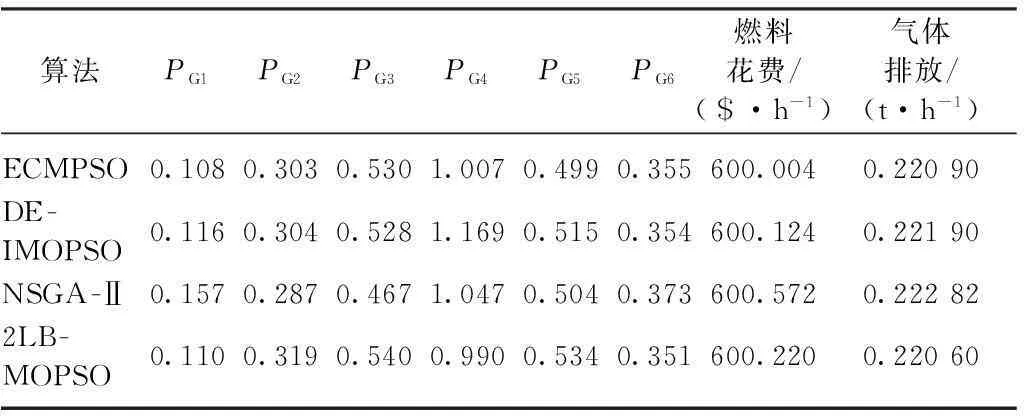
表3 不同算法在情况1中燃料花费最小的运算结果

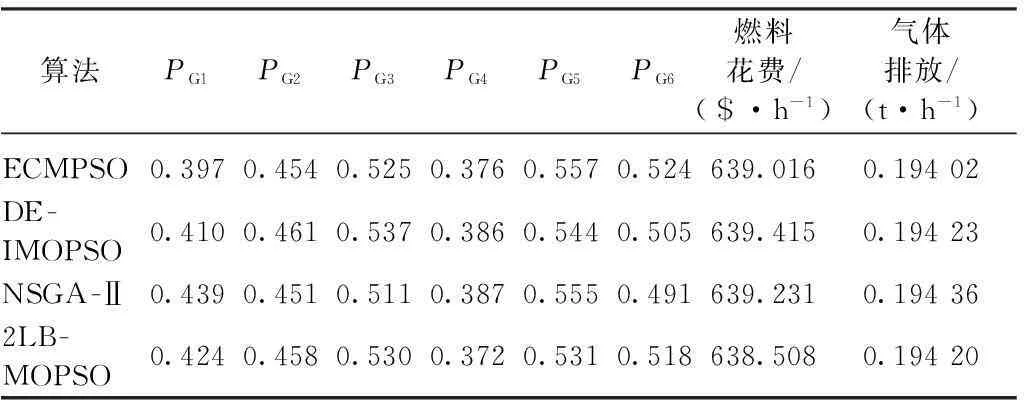
表4 不同算法在情况1中气体排放量最少的运算结果

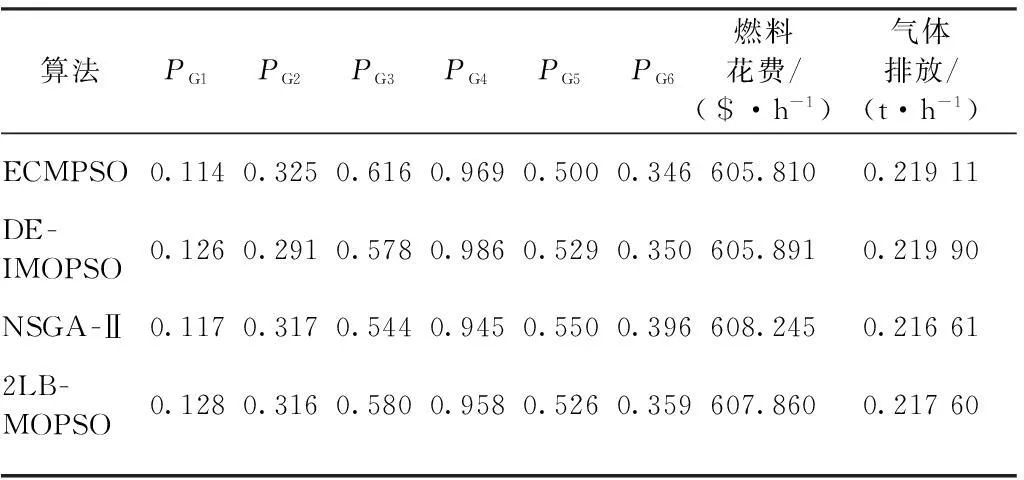
表5 不同算法在情况2中燃料花费最小的运算结果

表6 不同算法在情况2中气体排放量最少的运算结果

由表3和4可知，在情况1中ECMPSO算法求得的燃料花费最小值为600.004 ＄/h和气体排放量最小值为0.194 02 t/h，优于DE-IMOPSO、 NSGA-Ⅱ、 2LB-MOPSO 3种算法的结果.由表5和6可知，在情况2中ECMPSO算法求得的燃料花费最小值为605.810 ＄/h和气体排放量最小值为0.189 72 t/h,均优于DE-IMOPSO、 NSGA-Ⅱ、 2LB-MOPSO算法的结果.表3～6结果表明，ECMPSO算法取得了更好的最优解.ECMPSO算法在情况1和2中求得Pareto最优前沿如图3所示.由图3可以观察到，ECMPSO算法所得解遍布整个均衡面，在保持多样性的同时均匀分布性也较好.

(a) 情况1

(b) 情况2

4 结 语

针对电力系统的新型环境经济调度模式，提出了一种多种群协同微粒群优化(ECMPSO)算法,并将其与其他算法进行仿真试验对比，结果表明，ECMPSO算法在兼顾调度方案多样性的同时具有更高的求解精度，求出的调度方案分布均匀, 可为决策者提供更多有价值的候选调度方案.

[1] DEB K， PRATAP A， AGARWAL S, et al. A fast and elitist multi-objective genetic algorithm: NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation, 2002，6(2):182-197.

[2] 伍大清,郑建国. 基于混合策略自适应学习的并行粒子群优化算法[J].控制与决策，2013,28(7):1087-1093.

[3] 刘贞,张希良, 张继红,等.排污总量控制下的电力交易市场与排污权交易市场分析[J].电力系统保护与控制,2009,37(22):4-8.

[4] 卢有麟,周建中,覃晖,等.差分进化算法在电力系统环境经济调度中的应用[J].华中科技大学学报(自然科学版),2010(8):121-124.

[5] LIU G, PENG C, XIANG L. Economic-environmental dispatch using improved multi-objective particle swarm optimization [J]. Power System Technology, 2011, 35(7):139-144.

[6] HU W, LI Z S. A simpler and more effective particle swarm optimization algorithm [J]. Journal of Software, 2007, 18(4):861-868.

[7] WU D Q, ZHENG Z G. A dynamic multistage hybrid swarm intelligence optimization algorithm for function optimization[J]. Discrete Dynamics in Nature and Society, 2012, doi:10.1155/2012/578064.

[8] ZOU W P, ZHU Y L， CHEN H N, et al. Solving multi-objective optimization problems using artificial bee colony algorithm [J]. Discrete Dynamics in Nature and Society, 2011, doi:10.1155/2011/569784.

[9] HUANG V L, SUGANTHAN P N， LIANG J. Comprehensive learning particle swarm optimizer for solving multi-objective optimization problems [J]. International Journal of Intelligent Systems, 2006, 21(2)：209-226.

[10] 李密青，郑金华.一种多目标进化算法解集分布广度评价方法[J].计算机学报,2011,34(4)：647-664.

[11] HEMAMALINI S， SIMON P S． Emission constrained economic dispatch with valve-point effect using particle swarm optimization [C]//TENCON 2008 IEEE Region 10 Conference，India，2008．

[12] 徐丽青, 吴亚丽.求解环境经济调度问题的多目标差分粒子群优化算法[J].西安理工大学学报,2011,27(1):62-68.

[13] 瞿博阳，梁静，SUGANTHAN P N.双局部粒子群算法解决环境经济调度问题[J].计算机工程与应用,2014,5(11):45-53.

Power System Optimization Based on Multi-swarm Cooperation Collaborative Algorithm

LIUYong1，WUDa-qing1, 2, 3, 4, 5,SUNLi4,YANGZhi-ping4

(1. Artificial Intelligence Key Laboratory of Sichuan Province, Zigong 643000， China； 2. Computer Science and Technology Institute, University of South China, Hengyang 421001， China； 3. Key Laboratory of Intelligent Computing & Signal Processing, Ministry of Education, Anhui University, Hefei 230039， China； 4. Glorious Sun School of Business and Management, Donghua University, Shanghai 200051, China； 5. Key Laboratory of Agri-Informatics, Ministry of Agriculture, Beijing 100081， China)

An effective co-evolutionary multi-swarm particle swarm optimization (ECMPSO) is proposed for environmental-economic dispatch (EED), which is a complicated multi-objective constrained problem. The strategies such as multi-swarm, new particle swarm optimization (PSO) update as well as restructuring topology structure strategy with dynamic population in period are introduced in ECMPSO, so the algorithm has strong global search ability and good robust performance. Some typical multi-objective optimization functions are tested to verify the algorithm, the results show that the proposed algorithm has superior performance of faster convergence speed and strong ability to jump out of local optimum. The proposed algorithm is applied to solve the EED problem of a power system, experimental results demonstrate the successful application of ECMPSO, compared with other methods, ECMPSO outperforms in globe convergence and the diversity of the Pareto set with higher effectiveness and robustness.

cooperation collaborative optimization; multi-swarm optimization； particle swarm optimization； environmental economic dispatch

1671-0444(2016)01-0110-07

2014-09-25

四川省人工智能重点实验室基金资助项目(2015RYJ01)；湖南省科技计划资助项目(2015JC3089)；教育部计算智能与信号处理重点实验室基金资助项目(2014C16304)；上海市自然科学基金资助项目(15ZR1401600)；农业部农业信息服务技术重点实验室基金资助项目(2015-AIST-02)；四川省模式识别与智能信息处理重点实验室基金资助项目

刘 勇(1981—)，男，四川自贡人，实验师，硕士，研究方向为复杂系统优化.E-mail:24297633@qq.com

伍大清(联系人)，女，讲师，E-mail:dqw_1982@126.com

TM 734

A