纤维截面形状对纤维捕集效率及压力损失的影响

赵洪亮, 付海明, 雷陈磊, 张 杰, 冯 丰, 朱 辉

(东华大学 a.环境科学与工程学院； b.国家环境保护纺织污染防治工程技术中心， 上海 201620)

纤维截面形状对纤维捕集效率及压力损失的影响

赵洪亮a, b, 付海明a, b, 雷陈磊a, b, 张 杰a, b, 冯 丰a, b, 朱 辉a, b

(东华大学 a.环境科学与工程学院； b.国家环境保护纺织污染防治工程技术中心， 上海 201620)

为研究纤维截面形状对纤维过滤器性能的影响，采用Visual Basic 的应用程序版(VBA)随机生成不同几何截面形状的虚拟纤维过滤介质，通过计算流体动力学(CFD)技术求解流体在纤维介质流动的动量方程，得出不同几何截面形状纤维的压力损失.采用拉格朗日方法统计被纤维捕集颗粒数，获得纤维介质的捕集效率.采用质量因子综合评价模拟纤维过滤介质的过滤性能，研究不同几何截面形状纤维的异型度和形状系数对其捕集效率、压力损失以及质量因子的影响.模拟结果表明：压力损失随着形状系数的增大而增大；在填充率小于0.20时，三叶形纤维的捕集效率最高且压力损失最大；异形度、形状系数大的纤维对直径小于2 μm的颗粒具有较好的捕集效果；在纤维直径为30 μm时，对于颗粒直径小的粒子，三叶形纤维的综合过滤性能最好，而当纤维直径为5 μm时，圆形纤维的质量因子最高.

纤维过滤器； 异形纤维； 异形度； 形状系数； 捕集效率； 扩散

随着现代工业的发展，空气污染越来越严重.纤维过滤器是控制空气污染的有效设备，研究纤维过滤器的性能显得尤为重要[1].近年来，国内外许多学者对纤维过滤器的特性进行了研究，但大多数研究仅针对圆形纤维过滤介质，也有一些研究针对非圆形纤维的研究，如椭圆[2]、正方形或长方形[3-5]，以及“+”形、“T”形、“O”中空形[6].其中比较经典的有通过Zhukovsky转换探讨弧形纤维的流场[7]，文献[8]在文献[7]的基础上，研究了弧形纤维结构对纤维过滤器性能的影响.文献[9]讨论了不同的尺寸和纵横比的内部结构的三叶形纤维对压力损失和捕集效率的影响.文献[10]对圆形、方形、椭圆形、三叶形纤维进行了研究.但现有文献均采用单纤维模型，忽略了纤维与纤维之间对流场的影响.为此，本文采用多纤维模型，将抽象复杂的纤维形状假设成规则具体的椭圆形、三叶形、三角形、正方形、六边形，并与圆形纤维做对比，研究不同截面形状纤维对纤维过滤器性能的影响，旨在获得纤维异形度及纤维形状系数与纤维介质压力损失、捕集效率以及质量因子间的定性关系，为纤维过滤介质的优化设计提供理论参考.

1 研究方法

1.1 计算模型的建立

本文是以Visual Basic 的应用程序版(VBA)开发技术为平台，以AutoCAD软件为基础,开发出生成随机纤维的程序，导入CAD中生成随机虚拟纤维过滤介质模型，VBA程序主要通过控制纤维的直径、孔隙率及根数等参数来生成不同异形度、形状系数、填充率及直径的纤维模型. 为了确保模拟收敛于精确值，使过滤器前段流场均匀，后端流场不受过滤介质的影响，参照文献[9]，将过滤器前端延长部分距离设置为35(a+b)，过滤器后端延长部分设置为15(a+b)，其中，a为纤维直径，b为纤维间的最小距离.模拟计算流域如图1所示.

图1 纤维二维随机分布模型Fig.1 Two-dimensional random distribution model of fiber

1.2 边界条件的定义和网格划分

将气流进入的边界设置为速度入口，气流出口设置为压力出口，两侧的边界设置为对称边界条件.在模拟之前对模型进行了网格无关性测试，并对比三角形网格和方形网格对捕集效率的影响. 结果表明，当纤维直径为20～30 μm，每根纤维表面网格数从10增加到100以上时，纤维捕集效率从刚开始的趋近于1逐渐减小并趋于平稳，相同网格密度情况下，三角形网格收敛速度明显快于其他几种网格，所以本文采用三角形网格，且每根纤维表面选取网格数为100，并在纤维表面以及进出口边界采用网格加密技术，以增强计算精度.

1.3 研究方法的可靠性分析

为验证模拟方法的可靠性，本文针对几何截面为圆形的纤维，对其进行压力损失及捕集效率模拟计算，并与相关文献进行对比分析.

1.3.1 捕集效率

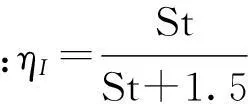
(1)

将式(1)代入对数穿透律公式

(2)

得到过滤介质总捕集效率计算式：

(3)

图2为模拟结果与式(3)计算结果的对比.模拟计算中参数设定如下：α=0.16, v=0.6m/s， df=30μm.由图2可知，捕集效率随着被捕集颗粒直径的增加呈抛物线型增加.对比模拟数据与式(3)计算值可知，模拟结果与理论计算结果中捕集效率的变化趋势基本一致，但式(3)计算值大于模拟值.

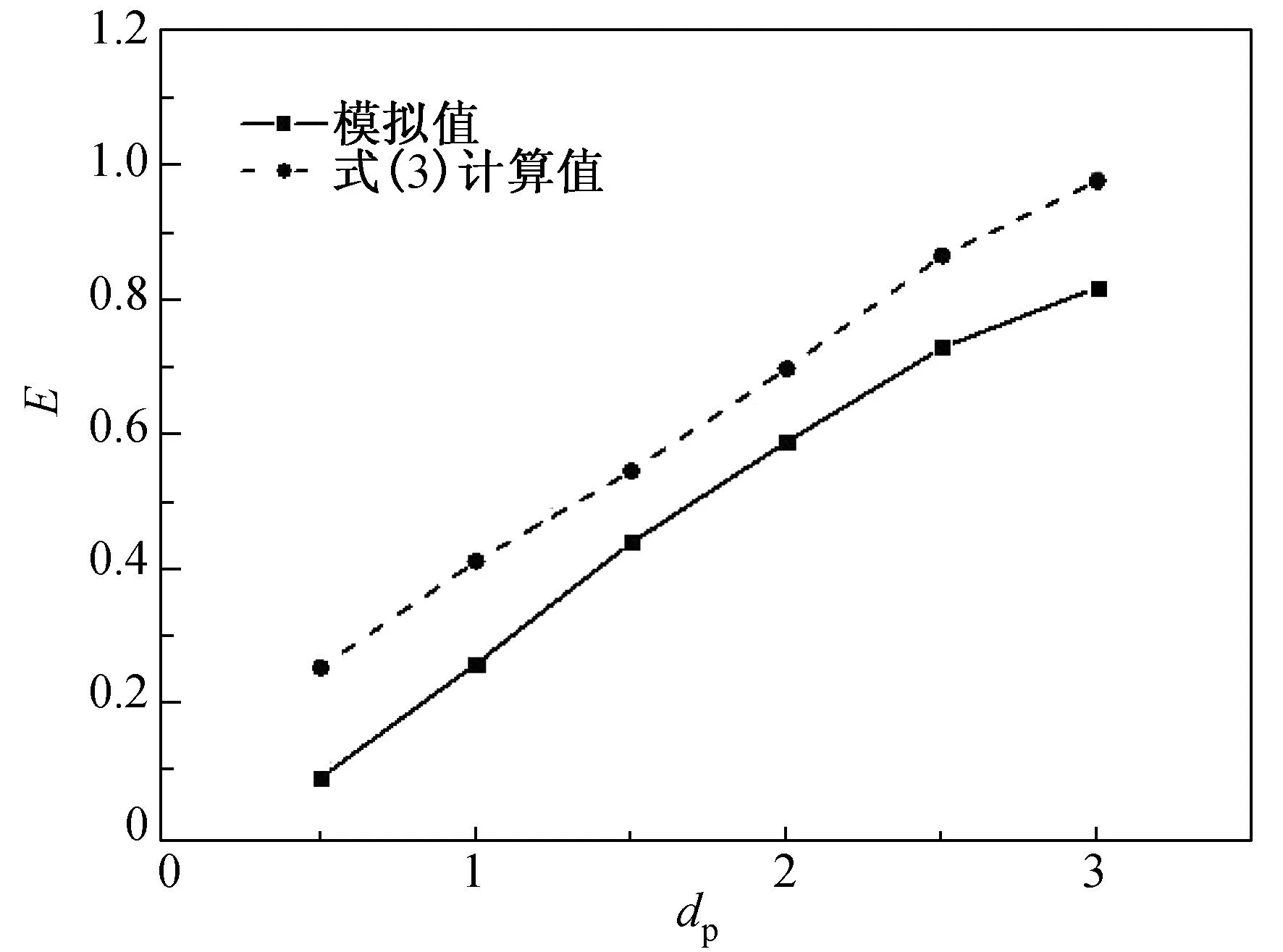
图2 捕集效率模拟结果与计算值比较Fig.2 Comparison between simulated collection efficiency and the calculated values

1.3.2 压力损失

本文采用Davies[14]压力损失半经验计算公式预测过滤介质的压力损失，如式(4)和(5)所示.

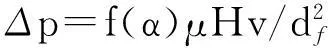
(4)

(5)

其中：H为纤维的厚度.

式(5)适用于填充率为0.6%～30%范围内的情况，是工程上普遍接受的一个压力损失模型.

图3 压力损失的模拟结果与计算结果对比Fig.3 Comparison of simulation results and calculated results of pressure drop

图3为模拟结果与式(4)计算结果的对比.模拟计算中参数设定如下：α=0.16,df=30 μm.由图3可知，随着过滤速度的增大，压力损失逐渐增大.对比两条曲线可知，计算得出的压力损失稍大于模拟得出的压力损失，但两条曲线非常接近，表明模拟计算结果与Davies[14]压力损失理论预测结果非常吻合.

1.4 纤维异形度与形状系数计算

本文选用异形度和形状系数[15-16]作为评价不同几何截面形状纤维的特征参数，两者的计算式如式(6)和(7)所示.

B=(1-r/R)

(6)

T=l2/A

(7)

其中：B为纤维异形度；R为异形截面外接圆半径；r为异形截面内接圆半径；T为纤维的形状系数；l为纤维截面的周长；A为纤维截面的面积.经计算常见的几种不同几何截面形状纤维的异形度和形状系数如表1所示.

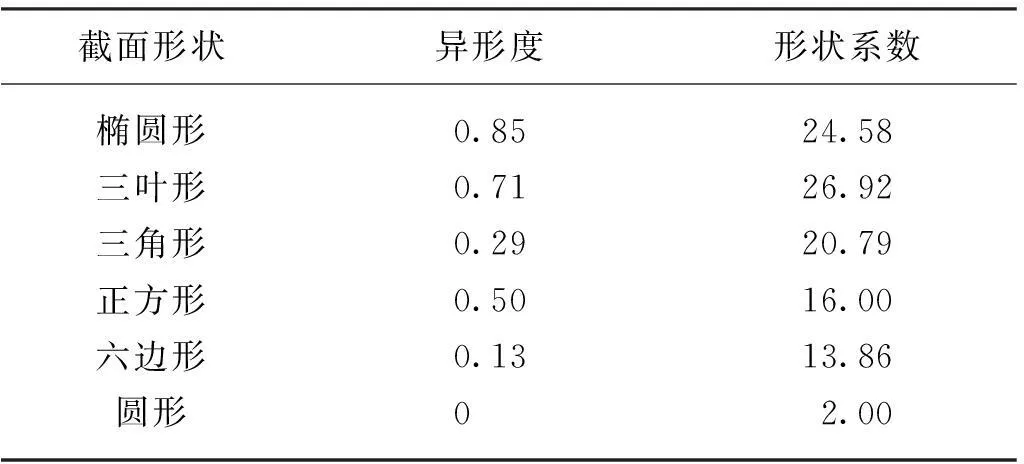
表1 不同截面形状纤维的异形度和形状系数值

2 数值计算

通常单丝直径为30 μm称为粗纤维；直径为10～20 μm称为中级纤维；直径为3～10 μm称为纺织纤维.本文主要讨论粗纤维及纺织纤维，分别取纤维直径为5 和30 μm时纤维过滤器对直径为1～3 μm颗粒的捕集效果.由于一般纤维滤料的填充率在0.01～0.30，因此，本文选取填充率为0.08～0.25的不同异形度和形状系数的纤维模型，选择计算过滤速度为0.2～1.2 m/s.采用计算流体动力学(CFD)软件模拟计算.

采用拉格朗日方法，求解颗粒在纤维介质中的运动轨迹，并添加能量方程，主要考虑扩散和惯性碰撞机理，通过被纤维捕集颗粒数的统计，获得纤维介质的捕集效率.

通过拉格朗日离散模型(DPM)计算，获得颗粒在不同截面形状纤维介质中的运动轨迹如图4所示.模拟计算中所需参数：α=0.16, v=0.6m/s，

(a) 椭圆形

(b) 三叶形

(c) 三角形

(d) 正方形

(e) 六边形

(f) 圆形

由图4可以看到，小颗粒粒子在流场中的布朗运动以及颗粒在不同截面纤维模型中随着气流的扰动情况.

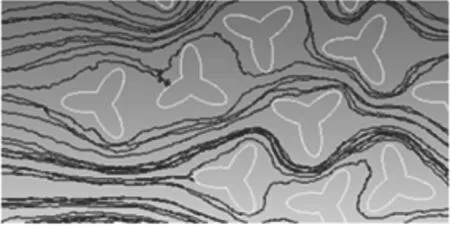
当模拟参数为α=0.16, v=0.6m/s情况下，不同截面形状纤维模型的涡流图如图5所示. 由图5可以清晰地看到，在相同过滤速度下，流体在不同截面形状的纤维模型内所产生的旋涡运动.

(a) 椭圆形

(b) 三叶形

(c) 三角形

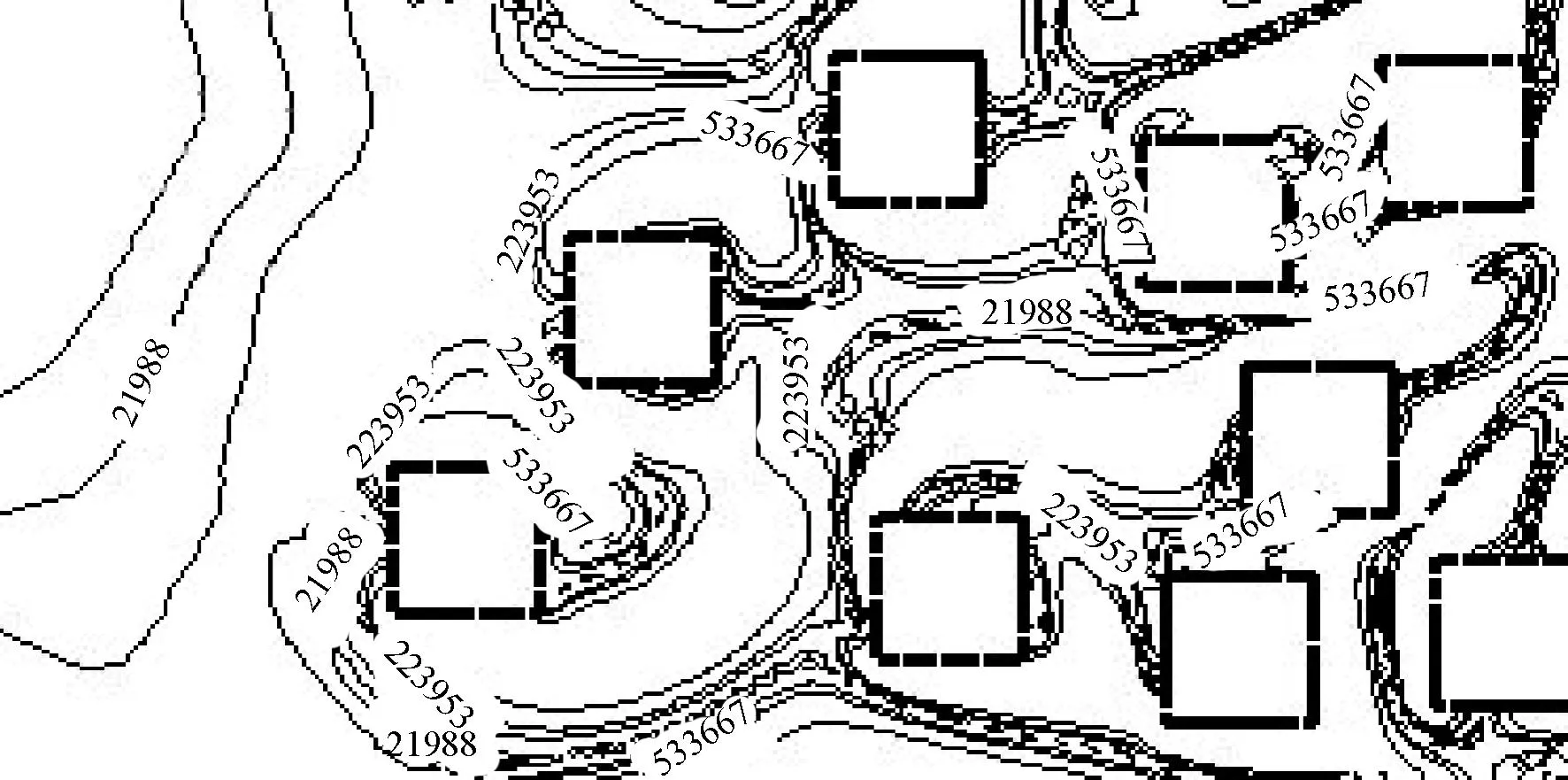
(d) 正方形

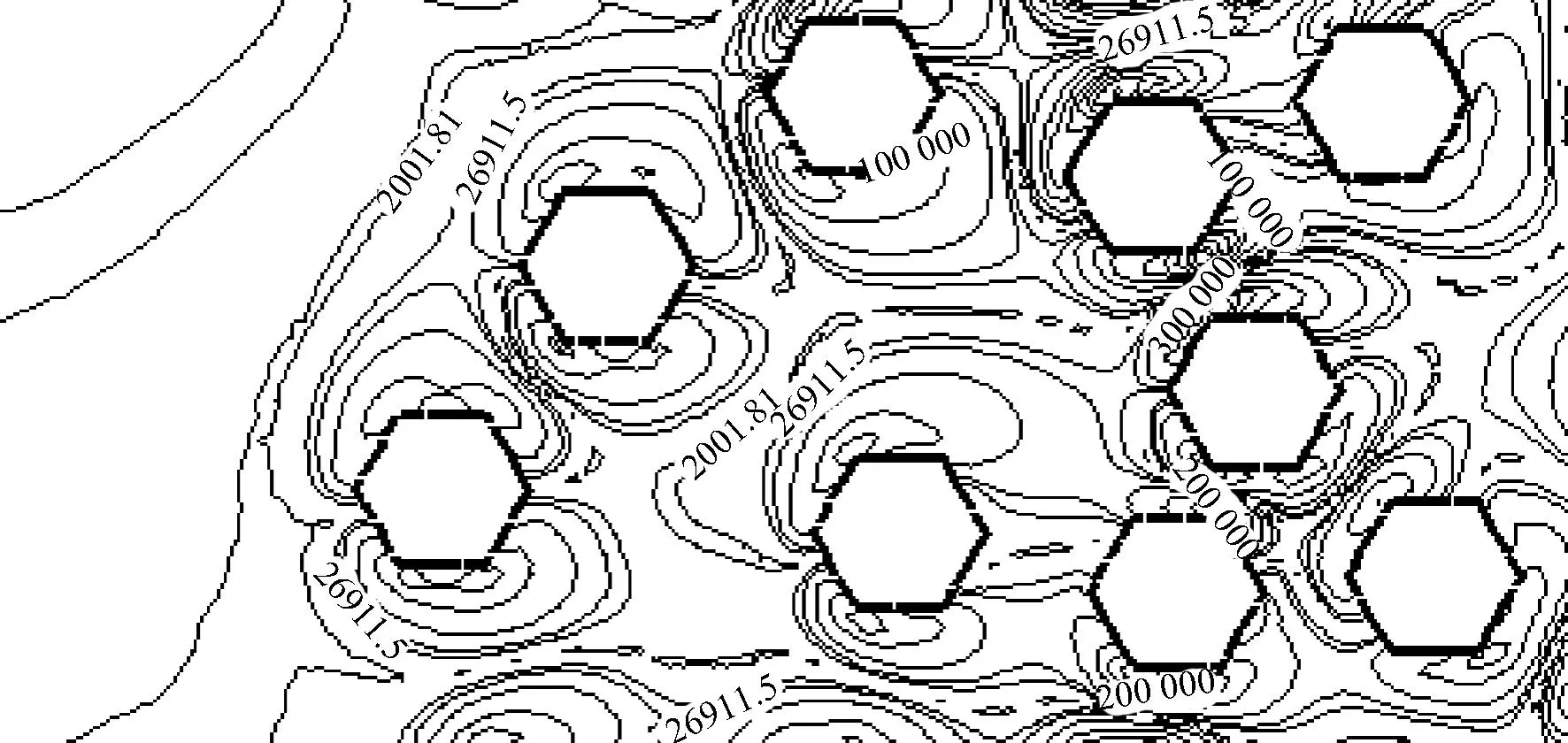
(e) 六边形

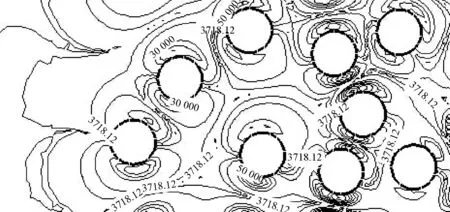
(f) 圆形

3 结果分析与讨论

3.1 捕集效率与异形度和形状系数的关系

当α=0.16，dp=2.5 μm，df=30 μm时，不同过滤速度下捕集效率与纤维异形度及形状系数的关系如图6所示.由图6可以看出，随着过滤速度的增加，捕集效率不断增加.当过滤速度为0.2和0.4 m/s时，随着截面异形度的增加，纤维的捕集效率先增加后减小；随着形状系数的增加，纤维的捕集效率增加.当过滤速度增加至0.6 m/s时，纤维的捕集效率出现明显的波动.

当v=0.6 m/s，dp=2.5 μm，df=30 μm时，不同填充率下捕集效率与纤维异形度和形状系数的关系如图7所示.

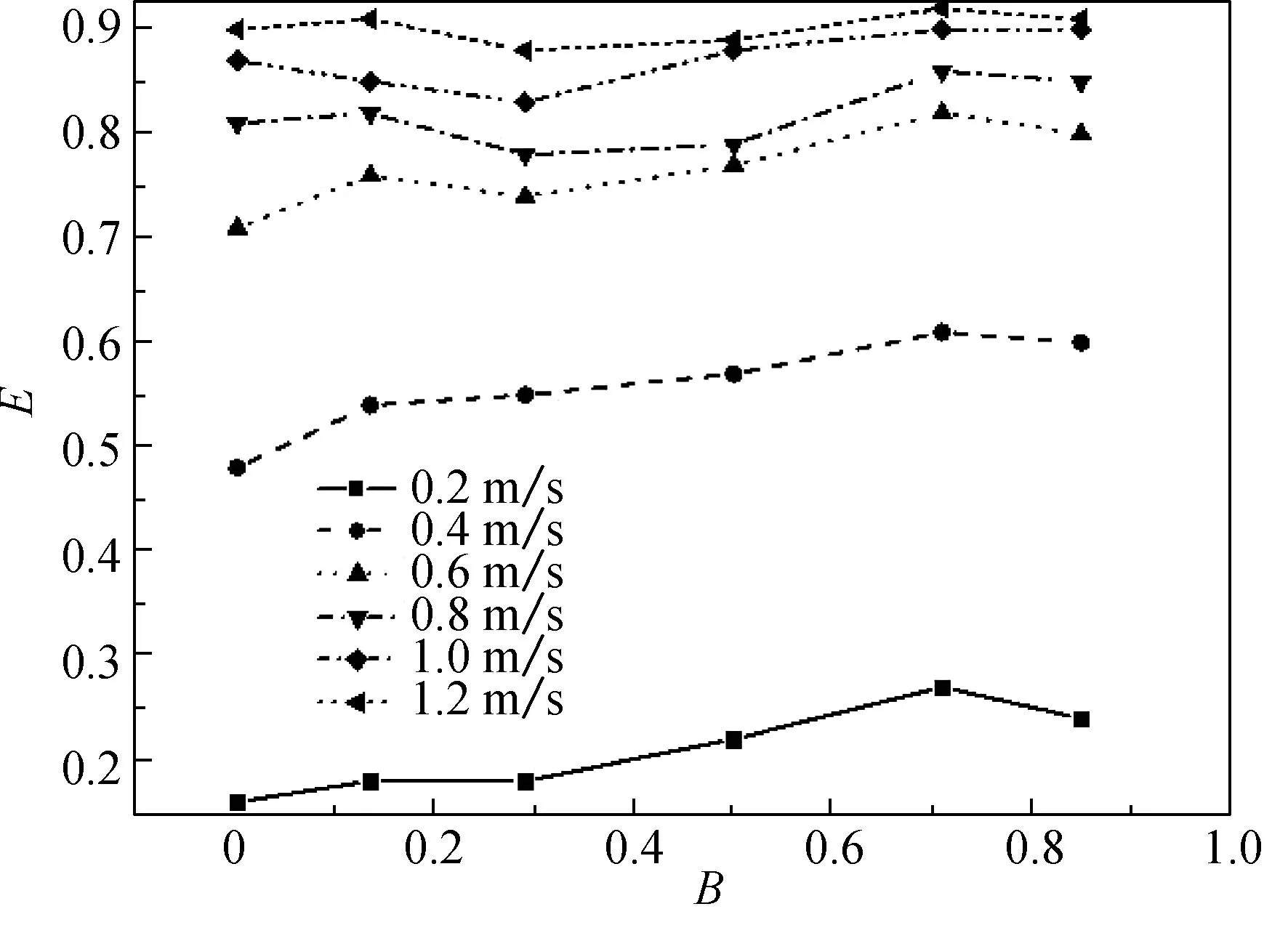
(a) 异形度

(b) 形状系数

(a) 异形度

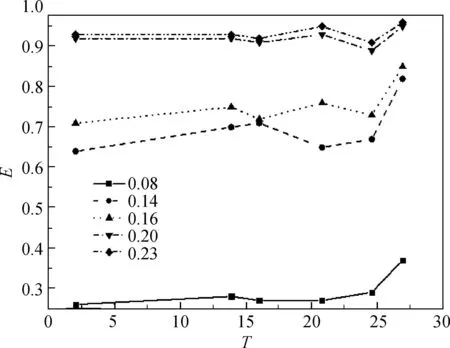
(b) 形状系数

由图7可以看出，捕集效率随着填充率的增加而增加；相同填充率条件下，三叶形纤维对于微粒的捕集效率高于其他几种截面形状纤维；当填充率大于0.20后再继续增大时，捕集效率变化很小.由图7(b)可知，在填充率较小时，捕集效率随着形状系数增大整体呈比较明显的增大趋势；当填充率由0.20继续增大时，捕集效率出现波动.

3.2 压力损失与异形度和形状系数的关系

填充率为0.16，不同过滤风速和纤维直径下压力损失与纤维的异形度的关系如图8所示.对比图8(a)和(b)可知，在相同填充率的条件下，相比于纤维直径为5 μm的模型，纤维直径为30 μm的模型压力损失随着过滤风速的变化较小，且随着异形度的变化也较平缓.

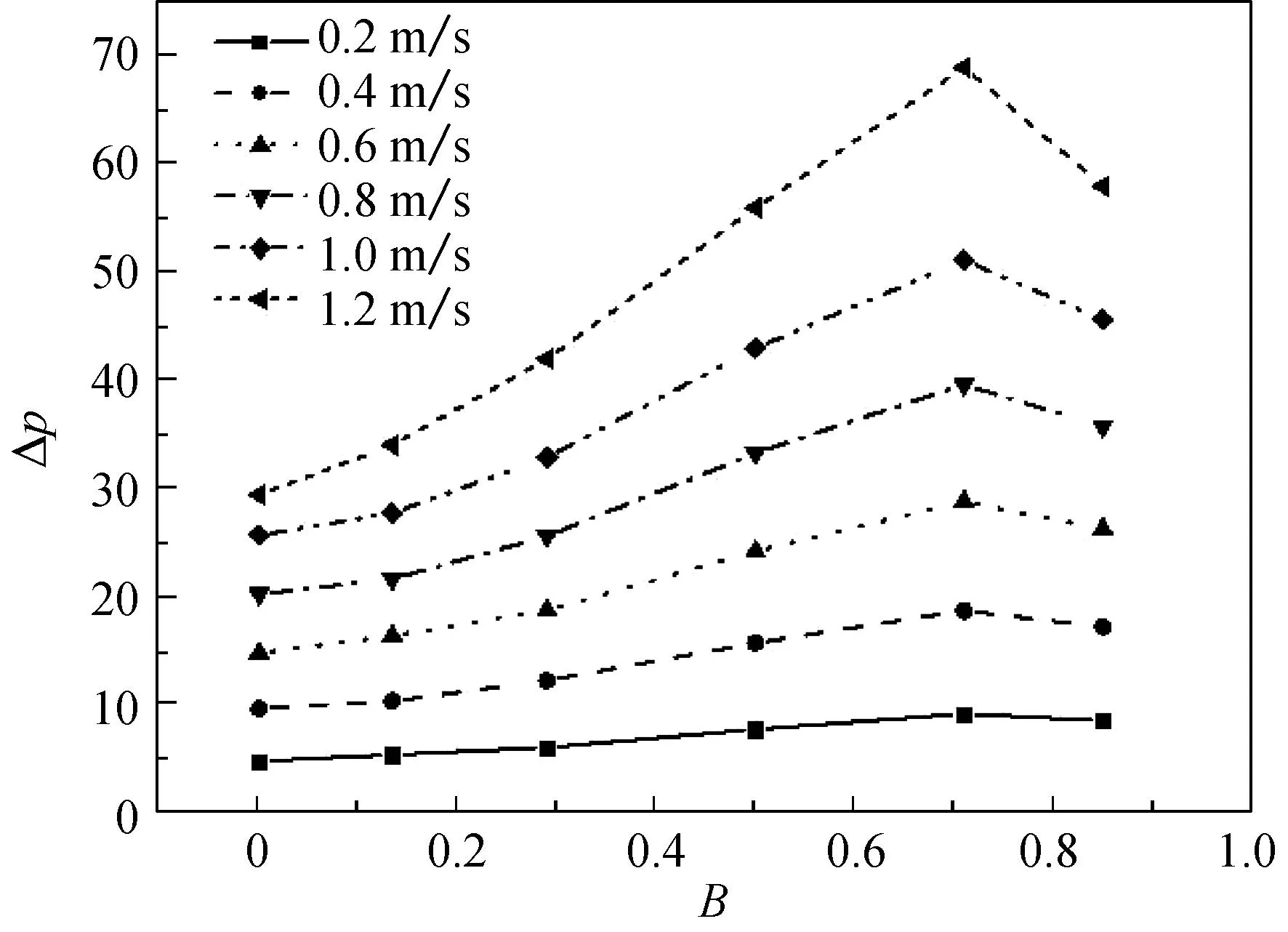
(a) df=30 μm

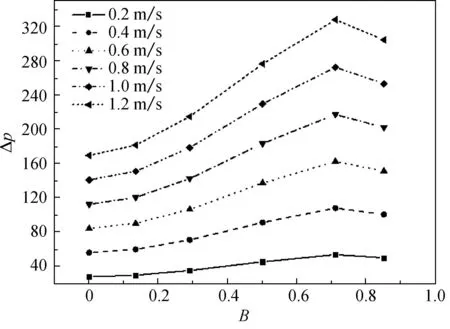
(b) df=5 μm

填充率为0.16，不同过滤速度和纤维直径下压力损失与纤维形状系数间的关系如图9所示.由图9可知，在两种不同纤维直径下，纤维过滤器的压力损失均随着纤维形状系数的增加而增加.

(a) df=30 μm

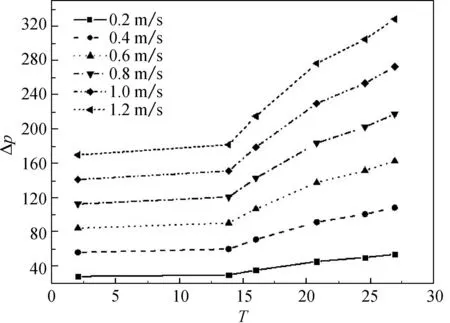
(b) df=5 μm

3.3 异形纤维优化分析

通常纤维过滤介质的压力损失越大，捕集效率越高，但理想状态是压力损失小而捕集效率高.因此，本文引入质量因子对异形纤维进行讨论，质量因子是衡量纤维过滤性能的综合指标，它综合考虑了捕集效率和压力损失的影响，其计算式如式(9)所示.

(8)

其中：Y为质量因子;E为纤维捕集效率;Δp为压力损失.Y值越大表示综合过滤性能越好.

当纤维直径分别为30和5 μm时，不同粉尘颗粒直径下质量因子与异形度的变化关系如图10所示.由图10可以看出，随着颗粒直径的增大，纤维综合过滤性能不断提高.在纤维直径等于30 μm时，对于颗粒直径比较小的粒子，随着纤维异形度的增大，质量因子Y先增大后减小，即三叶形的纤维综合过滤性能比较好；而对于颗粒直径较大的粒子，质量因子随着纤维异形度的增大先减小后增大，综合而言，圆形截面纤维的综合过滤性能较好.而对于当纤维直径为5 μm时，质量因子随着异形度的增加先减小后增大，对于颗粒直径比较小的粒子，三叶形纤维的质量因子最低，对于粒径比较大的颗粒，三角形纤维的质量因子最低，圆形截面纤维的质量因子最高.

(a) df=30 μm

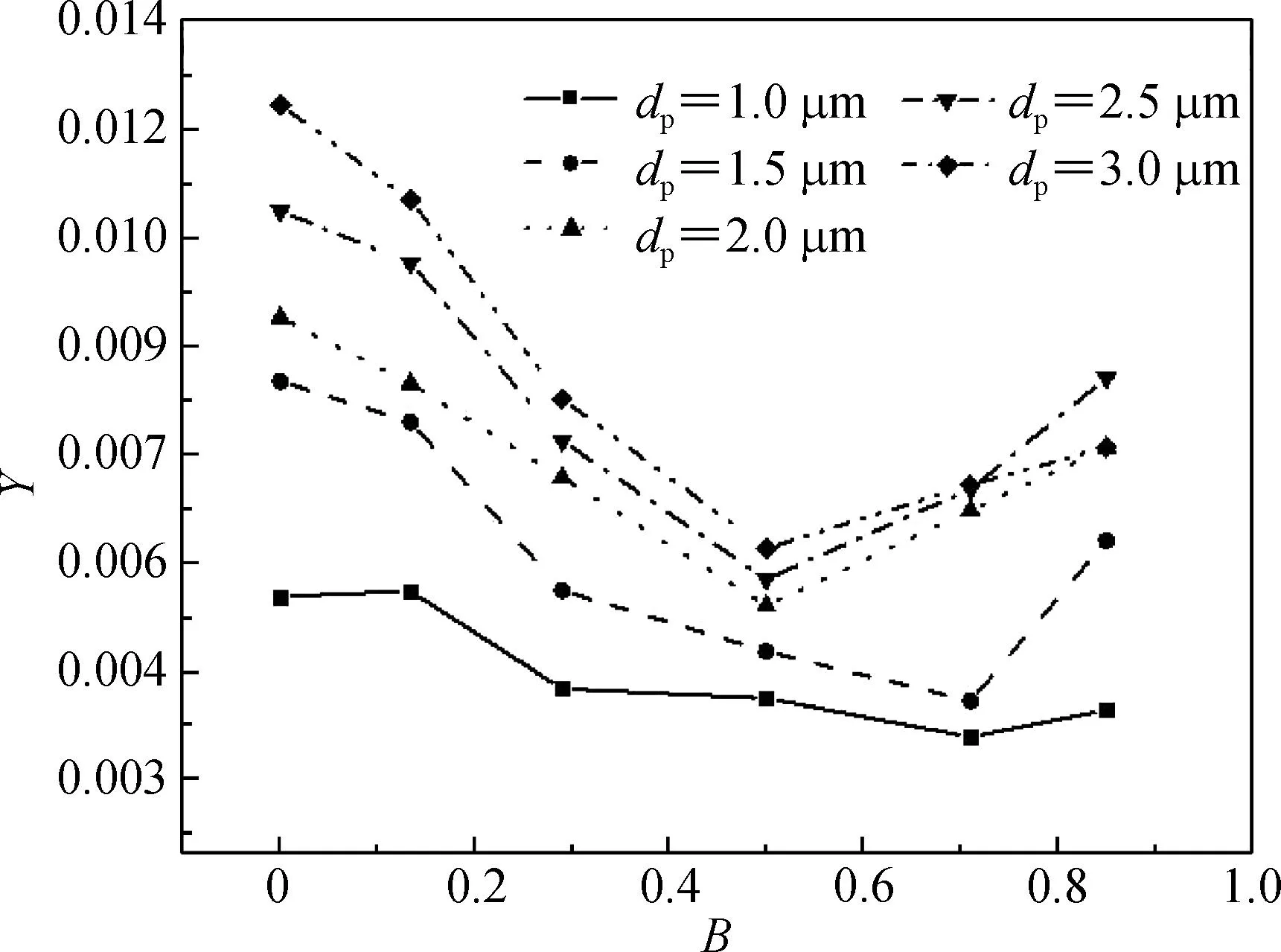
(b) df=5 μm

当纤维直径分别为30和5 μm时，不同粉尘颗粒直径下质量因子与形状系数的关系曲线如图11所示.由图11可知，当颗粒直径较小时，质量因子随着形状系数的变化不明显，而随着颗粒直径的增大，形状系数对于质量因子的影响也相应增大.

(a) df=30 μm

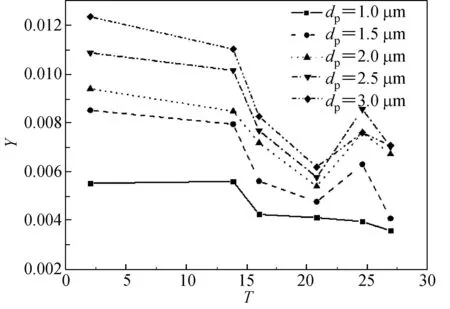
(b) df=5 μm

Fig.11 Relationship between quality factor and shape factor

4 结 语

本文采用拉格朗日方法，分别对不同异形度和形状系数的纤维的捕集效率和压力损失进行模拟研究，引入综合过滤性能评价指标(质量因子)分析不同几何形状纤维的过滤性能，得到下述结论.

(1) 纤维异形度和形状系数在过滤速度为0～0.8 m/s时，对捕集效率的影响比较大，纤维的捕集效率随着形状系数的增大而增大，三叶形纤维的捕集效率高于其他几种形状；在其他条件相同的情况下，填充率越大捕集效率也越大，且异形度和形状系数对于填充率小于0.20的纤维影响较明显.

(2) 纤维压力损失随着形状系数的增大而增大，随着异形度的增大先增大后减小，即相同纤维当量直径、填充率、过滤速度和粒径条件下，纤维压力损失由大到小依次为三叶形、三角形、正方形、六边形、圆形，且纤维的当量直径越小，纤维的异形度和形状系数对压力损失的影响越大.

(3) 在其他条件相同的情况下，纤维直径为30 μm时，对于颗粒直径小的粒子，三叶形纤维的质量因子最大，即过滤性能最好，随着颗粒直径的增大，质量因子的变化会出现波动.而纤维直径为5 μm时，圆形纤维的质量因子最高.

[1] 付海明,沈恒根.纤维过滤器过滤理论的研究进展[J].中国粉体技术,2003(1):41-46.

[2] WANG W X, XIE M L, WANG L P. An exact solution of interception efficiency over an elliptical fiber collector[J]. Computer and Fluids, 2013,88:354-362.

[3] FARDI B, LIU B Y H. Flow field and pressure drop of filters with rectangular fibers[J].Aerosol Science & Technology, 1992,17:36-44.

[4] FARDI B, LIU B Y H. Efficiency of fibrous filters with rectangular fibers[J]. Aerosol Science & Technology, 1992, 17:45-48.

[5] OUYANG M, LIU B Y H. Analytical solution of flow field and pressure drop for filters with rectangular fibers[J]. Aerosol Sci, 1998,29(1):187-196.

[6] USHE Z. The effect of different shaped cross-sectional microfibers on filtration[C]//Advances in Filtration and Separation Technology. 1993:146-147.

[7] WANG W X, HE Q, CHEN N, et al. A solution for potential flow over an arc fiber[J]. Thermal Sci, 2012,16:1564-1568.

[8] XIE M L， HE Q， WANG W X， et al. An exact solution of interception efficiency over a circular-arc fiber[J]. Computers & Fluids, 2013, 88:354-362.

[9] FOTOVATIA S, TAFRESHIA H V, POURDEYHIMI B. Analytical expressions for predicting performance of aerosol filtration media made up of trilobal fibers[J]. Journal of Hazardous Materials, 2011,186(2/3):1503-1512.

[10] HOSSEINI S A, TAFRESHI H V. On the importance of fibers’ cross-sectional shape for air filters operating in the slip flow regime[J]. Powder Technology, 2011, 212(3):425-431.

[11] HENRY F S, ARIMAN T. An evaluation of the Kuwabara model[J]. Particulate Science and Technology, 1983,1(1):1-20.

[12] GABRIEL I T. Separation of airborn dust in deep-bed filtration[M]. Boca Roton: Lewis Publishers,1989:236-240.

[13] KVETOSLAV R. Advance in aerosol gas filtration[M]. Boca Roton: Lewis Publishers, 1997:345-365.

[14] DAVIES C N. Air filtration[M]. London: Academic Press, 1973.

[15] 王府梅，赵林，裴豫明，等.纤维截面异形度的研究[J].纺织学报，1991,12(7):300-304.

[16] 魏赛男,崔淑玲.纺丝工艺及截面形状对异形纤维性能的影响[J].毛纺科技，2005(11):43-46.

Effect of Fibers’ Cross-Sectional Shape on Fiber Collection Efficiency and Pressure Drop

ZHAOHong-lianga, b，FUHai-minga, b,LEIChen-leia, b,ZHANGJiea, b,FENGFenga, b，ZHUHuia, b

(a. School of Environmental Science and Engineering； b. State Environmental Protection Engineering Center for Pollution Treatment and Control in Textile Industry, Donghua University, Shanghai 201620, China)

In order to study the influence of fibers’ cross-sectional shape on properties of fiber filter, Visual Basic for Applications (VBA) was used to generate different cross-sectional shapes of virtual fiber filter media randomly. By simulation calculation of the computational fluid dynamics (CFD), the momentum equations of fluid in fiber medium can be solved, so the pressure drop of different cross-sectional shapes of fibers was obtained. Through the statistics particulate number by fiber traps can gain fiber medium collection efficiency by using the Lagrange method. Filtration performance of the fiber filter media was simulated by quality factor comprehensive evaluation, and the effects of different alien degrees and shape factors on the collection efficiency, pressure drop and quality factor were studied. The simulation results show that the pressure drop increases with the shape factor increasing. In the filling rate less than 0.20, the collection efficiency of trilobal fibers is the highest and its pressure drop is the biggest as well. The fiber has good trapping effect for diameters less than 2 μm particles. When the fiber diameter is equal to 30 μm， for small particles,trilobal fibers have the best filter comprehensive performance.When the fiber diameter of 5 μm, quality factor of round fiber is the highest.

fiber filter; profiled fiber; alien degree; shape factor; collection efficiency; diffusion

1671-0444(2016)01-0086-07

2014-12-03

国家自然科学基金资助项目(51178094; 41371445)

赵洪亮(1989—)，男，黑龙江哈尔滨人，硕士研究生，研究方向为建筑环境空气质量控制.E-mail：harlan_zhao@sina.com

付海明(联系人)，男，高级工程师，E-mail：fhm@dhu.edu.cn

TQ 021；TU 834；X 701.2

A