资料匮乏地区径流降尺度模型构建及预测

夏依拉·居尔艾提 ，杨 涛(河海大学水文水资源与水利工程科学国家重点实验室, 南京 210098)

0 引 言

水是干旱区的命脉，中亚干旱区四面环山，径流补给主要来自于冰川和积雪，受气候影响较大，随着气候变化的进一步加剧，冰川退缩、雪盖减少，对水资源产生了重大的影响。

目前研究气候变化对水资源影响的常规方法是: 由全球气候模型GCM结合降尺度方法用来驱动水文模型而产生径流的计算结果。但由于一般流域水文模型需要大量的水文气象观测资料(降水、气温、径流)，而我国大部分西部地区，水文气象观测站网非常低，很多中高山带(2 500 m以上)基本上属于无资料地区，水文气象资料严重匮乏，故常规的流域水文模型根本不能使用，迫切需要研究一种简便快捷同时具有一定精度的径流预测模型。径流降尺度方法简单易行，所需资料少，同时精度不低于常规方法，适合于资料匮乏地区的气候变化影响研究，近来日益受到国内外学者的重视。

研究表明，很多方法都可用于径流降尺度模型构建，例如：人工神经网络(ANN)，广义线性模型(GLM)，关联向量机(RVM)，典型相关分析(CCA)等。Cannon[1]在加拿大不列颠哥伦比亚省21个流域利用人工神经网络构建径流降尺度模型，并与线性回归方法进行了对比，得出人工神经网络可以较好地捕捉到输入和输出之间复杂的非线性关系；Ghosh[2]应用关联向量机构建统计降尺度模型，模拟了印度的雨季径流，并结合GCM预测了未来气候情景下的径流趋势。其中人工神经网络(ANNs)可以很好地捕捉到输入和输出之间的非线性关系并且不需要对其中基本物理过程有深入的了解[3]，常被用来解决很多水文问题，但因其无法给出预报量模拟结果的不确定性，限制了ANNs在解决水文问题中的可用性。贝叶斯神经网络BNNs作为近来的一种较为新的方法，不仅能算出预报量的平均的模拟值，还可以估计预测的置信区间。最近，贝叶斯神经网络广泛地应用于模型的训练、选择和预测等。Zhang[4]等用4种类型的贝叶斯神经网络BNNs来估计美国两个流域的径流模拟的不确定性。

1 研究方法

1.1 神经网络模型结构

人工神经网络是具有很强的处理非线性问题能力的数据处理系统，适合于解决因果关系复杂的非确定性推理等问题，且自身具有自适应性能力、容错性等优良性能[5]。神经网普遍应用于输入输出之间复杂的非线性关系，输入矢量xt到目标函数的yi的映射，即yt=f(xt)+ε，其中f(xt)为神经网络结构：

(1)

式中：p为输入层节点数；M为隐含层节点数；αb为输出层阀值；αi为连接第i个输入到输出的权重；βj为连接第j个隐含层到输出的权重；γj0为第j个隐含层阀值；γji为连接第i个输入到第j个隐含层的权重；Ψ(t)为转移函数，取用双曲正切函数，即：Ψ(t)=tanh(z)。

通常，人工神经网络结构是固定的，即各神经元之间连接的个数固定的。

1.2 贝叶斯神经网络

一组指示函数可以表示特定的连接的有效性，神经网络结构就转变成为：

(2)

令I(ζ)为连接ζ的指示函数，若I(ζ)=1，此链接有效；若I(ζ)=0，此链接无效。

使∧为包含全部指示函数的矢量，使α=(α0,α1,…,αp)，β=(β1,…,βM)，γj=(γj0,γj1,…,γjp),γ=(γ1,…,γM) ，θ=(α∧,β∧,γ∧,σ∧)，其中α∧,β∧,γ∧分别表示α,β,γ中非零子集，因此可以用(θ,∧)来表示贝叶斯神经网络结构。为了对模型进行贝叶斯分析，需要指定以下分布：αi～N(0,σ2a)(i=0,…,p)，βj～N(0,σ2β)(j=1,…,M)，γji～N(0,σ2γ)(j=1,…,M)(i=0,…,p)，σ2～IG(v1,v2)，其中σ2α,σ2β,σ2γ,λ是需要人为确定的超参数，本文中取σ2α=σ2β=σ2γ=5,λ=10。

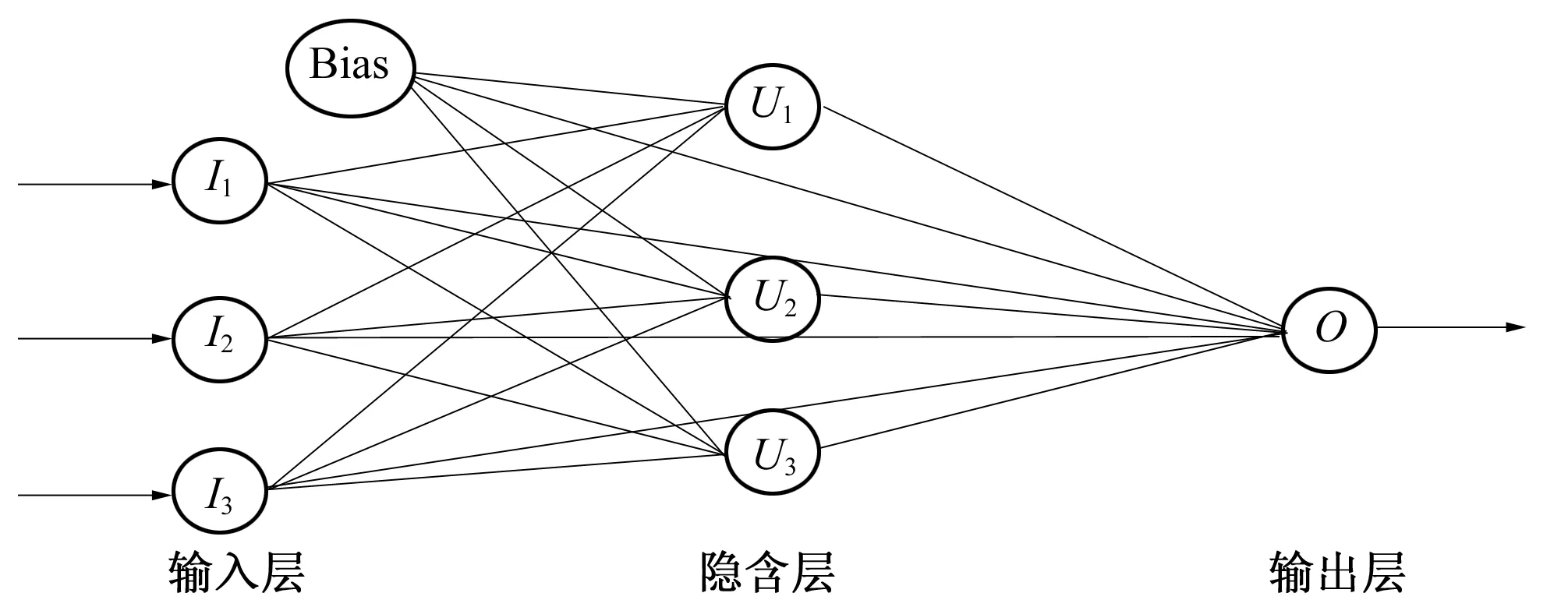
图1 贝叶斯神经网络模型示意图Fig.1 Schematic of bayesian neural networks

在传统神经网络训练中，选出一个最能反映观测数据的最佳网络结构；贝叶斯方法主要原理为在已知观测数据条件下，指导(θ,∧)的后验概率分布。在贝叶斯训练结构中，应用观测数据和参数及模型结构的先验知识来导出模型结构和参数的后验分布。已知数据集D={(x1,y1),(x2,y2),…,(xn,yn)},则：

(3)

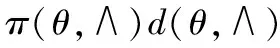
认为人工神经网络模拟误差服从均值为0，将标准差为σ的高斯白噪声分布，则得到的似然函数即为下式所示的表达式，可根据以下表达式进行抽样：

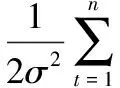
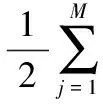
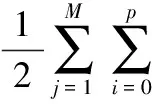
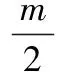
其中，m=∑pi=0Iαi+∑Mj=1Iβjδ(∑pi=0Iγj1)+∑Mj=1∑pi=0IβjIγji，当Z>0时，δ(Z)=1，否则δ(Z)=0。

贝叶斯神经网络中，取选出的样本的平均值为模拟值，即：

(4)

式中：K为所选的模型(θ,∧)的个数。

1.3 EMC

本文所选择的抽样方法为EMC方法，是结合了MCMC重要性抽样、遗传算法的学习能力、平行算法的空间多链搜索能力的一种贝叶斯抽样方法。EMC的一次迭代抽样中包含三个操作，分别为变异、交叉、交换，如图2所示，操作是否有效的判断服从各自的Metropolis原则[6]。

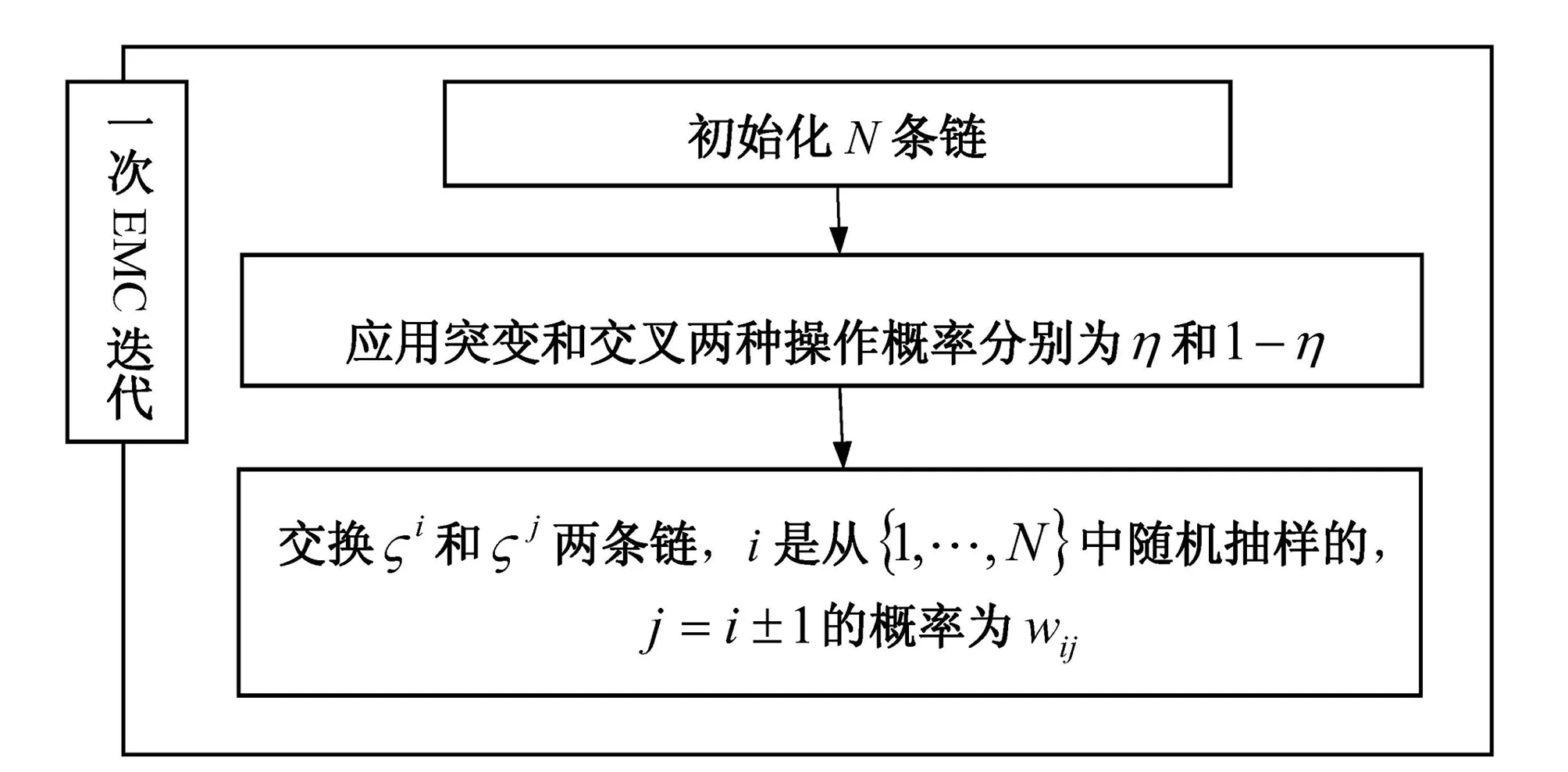
图2 一次EMC迭代过程示意图Fig.2 Schematic of one iteration of EMC

2 统计降尺度方法的建立

2.1 研究区及数据

叶尔羌河是塔里木河四源头之一，发源于克什米尔北部喀喇昆仑山脉的喀喇昆仑山口，流域范围东经74°28′～80°54′，北纬35°40′～40°31′之间。叶尔羌河流域由于南、西、北三面分别受喀喇昆仑山、帕米尔高原和南天山的阻挡，外来水汽较少，为典型的干旱大陆性气候，高山区的冰雪融水成为河川径流的最为主要的补给来源，流域多年平均冰川消融量约占出山口卡群站多年平均径流量的64.0%，雨雪混合补给占13.4%，地下水补给占22.6%[7]。

本文选用了叶尔羌河卡群站月平均径流(1954-2008年)，其中1954-2000年资料用来率定，2001-2008年用来验证统计降尺度模型。本文采用NCEP全球再分析日资料作为观测的大尺度气候资料，未来气候数据来自世界气候研究计划耦合模式比较计划第四代模式(CMIP5)中的几种模式，根据相关研究结果[8]，本文中选GFDL_ESM2G，GFDL_ESM2M，MIROC5等三种模式的RCP 4.5, RCP 6.0, RCP 8.5等3种情景的2011-2100年月平均数据进行预测。

2.2 气象预报因子的选择

逐步回归是多元回归中用以选择自变量的一种常用方法。在变量很多时，其中有的因素可能对因变量的影响不是很大，而且变量之间不完全相互独立的，可能有种种互作关系，在这种情况下，可以用逐步回归分析，进行因子的筛选。

基于流域范围内6个NCEP网格的所有待选预报因子，应用逐步回归方法(其中设置置信度α=0.15)进行筛选,最终优选出径流降尺度所需要的预报因子，如表1所示。

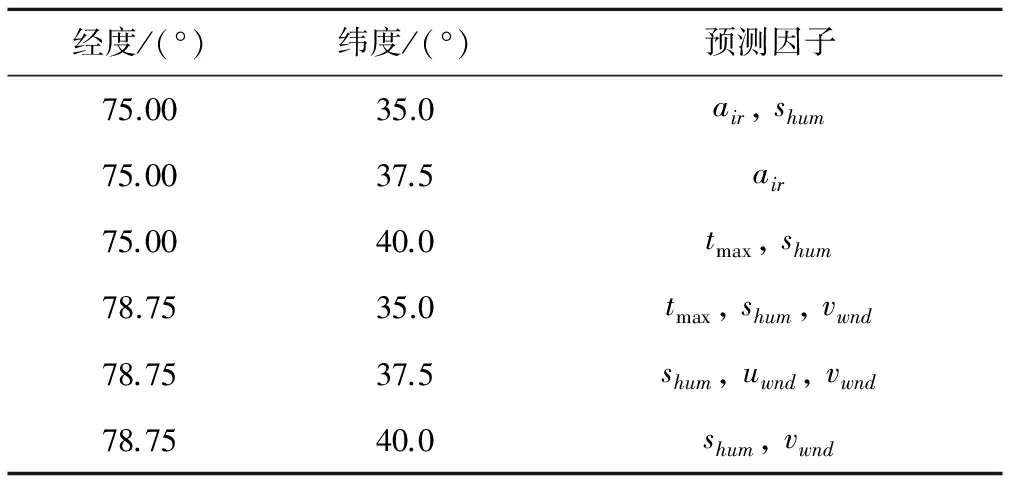
表1 应用逐步回归筛选出来的预报因子Tab.1 The input variables using stepwise selection method

注：air为近地面平均气温；tmax为近地面日最高气温；shum为近地面比湿；uwnd为地表经向风；vwnd为地表纬向风。

2.3 评价指标

为了系统评价降尺度效果，使用纳什效率系数Ens，相关系数R，均方根误差RMSE来衡量模型对径流量及其年际变化的捕捉能力。应用贝叶斯神经网络，可以估计预测结果的不确定性区间。为了定量地评估不同的隐含层节点条件下的不确定性区间，应用以下评价指标：90%不确定性区间所包含观测值的百分比(POC), 平均相对宽度(ARIL), 预测界限关于相应的观测值的平均对称度(AAD) (若AAD值小于0.5表明，观测径流基本在不确定性区间之内，AAD值越大，不确定性边界关于观测值越不对称)和平均偏离度(ADA)。

3 结果与分析

3.1 模拟能力对比分析

以筛选的预报因子为神经网络的输入，用卡群站月平均径流作为网络的期望输出,分别用贝叶斯神经网络和BP神经网络构建径流降尺度模型，评价神经网络统计降尺度法对卡群站月径流的模拟精度(表2)。可以看出，BP神经网络虽然在率定期模拟效果较优，但验证期较差，因为BP神经网络训练中，选出一个最能反映观测数据的最佳网络结构，不一定能很好地反映其他的数据序列，而贝叶斯神经网络取符合条件的多个神经网络结构的平均值作为模拟值，弥补了BP神经网络的不足，即率定期及验证期相关系数都达到0.9以上，效率系数也达到0.8。不同的隐含层节数对模拟效果影响不是很大，相对而言当隐含层节点M=4时，模拟效果较优,故本文中取隐含层节点数为4。贝叶斯神经网络最大的优点是，不仅能给出平均的模拟值，还可以定量估计模拟的不确定性区间(表2)，不同隐含层条件下的不确定区间，难以同时满足较高的覆盖度、较小的相对宽度、较大的对称性和较小的偏离度，当隐含层节点数M=4时，率定期覆盖度达到95%以上，验证期达到91%以上，相对M=5、6来说比较高，观测值基本在90%不确定性区间内；率定期及验证期AAD值都等于0.25，对称性也比较好；率定期相对宽度为2.56及偏离度为73.33，相对M=5、6来说都比较低；图3为当M=4时，率定期及验证期卡群站月平均径流观测值，基于贝叶斯神经网络的平均模拟值及90%不确定性区间。

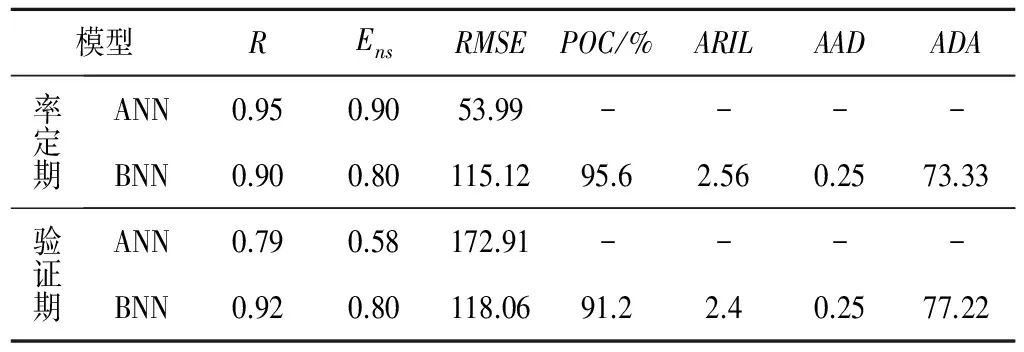
表2 两种模型对月径流模拟能力及不确定性区间的评估Tab.2 Assessment of the performance in monthly streamflow simulating and the uncertainty intervals for BNNs and ANNs

3.2 未来径流情景预测

应用已建立的贝叶斯神经网络，选用GFDL_ESM2G,GFDL_ESM2M, MIROC5等三种模式RCP4.5,RCP6.0,RCP8.5三种情景下的输出结果为气候强迫数据，对叶尔羌河未来3个时段[2011-2040年(2020年代),2041-2070年(2050年代)2071-2100年(2080年代)]卡群站的月平均径流进行预测。3种模式，3种情景下的径流预测值及90%不确定性区间如图4所示。由图4可见，GFDL_ESM2G,GFDL_ESM2M在相同情景下的月径流及其不确定性区间较为相似；MIROC5未来3个时段枯水期(10-4月)月径流普遍比前两个模式大，且其不确定区间宽度也较大。

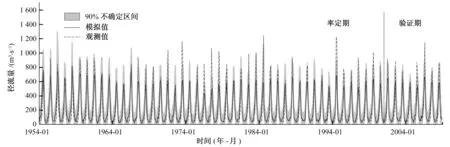
图3 率定期及验证期内径流降尺度模型模拟结果及90%不确定性区间Fig.3 The simulations of the streamflow downscaling in both calibration and validation period with 90% uncertainty intervals

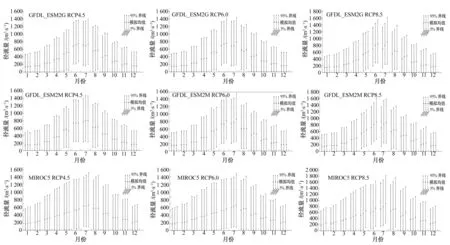
图4 3种模式3种情景下的径流预测平均值及90%不确定性区间Fig.4 Projected scenarios of streamflow with a 90% uncertainty interval in three future time horizons under three RCPs based on three selected GCMs

在未来气候变化情景下，卡群站年径流随时间推移均呈增加的趋势，与基准期(1961-1990年)相比，3种模式3种情景下，未来3个时段年径流变化范围分别为75%～92%，83%～110%，88%～127%。不同情景下的径流预测结果有差异，其中RCP8.5情景下的径流增加幅度比其他情景较明显，尤其是在2050年代和2080年代；主要原因是叶尔羌河径流以冰川补给为主，温度的逐年代升高，加速了山区冰雪资源的消融，对径流的影响也越来越显著。对选取的3个模型3个情景2010-2100年的气温数据进行分析，可知叶尔羌河流域平均气温明显升高，其中RCP8.5情景下气温升高的幅度较大，尤其是在2050年代及2080年代；以GFDL_ESM2G为例，RCP4.5情景下，与基准期(1961-1990年)平均气温相比，未来3个时段平均气温增加幅度分别为3.8,4.7,4.9 ℃；RCP6.0情景下，未来三个时段气温增加幅度为3.1,4.5,5.7 ℃；RCP8.5情景下，未来三个时段气温增加幅度为4.1,5.5,7.6 ℃；故RCP8.5情景下，年径流增加趋势较明显，例如：MIROC5 RCP8.5情景，在2080年代时段的年径流增加速率为2.2 m3/(s·a)。

不同月份的径流存在不同程度的增加趋势，其中9-4月份月径流变化趋势相对不明显，例如：GFDL_ESM2G RCP4.5情景下，1月份的径流增加速率为0.27 m3/(s·a)，MIROC5 RCP6.0情景下，10月份的径流增加速率为0.53 m3/(s·a)；5-8月份变化趋势较明显，例如：GFDL_ESM2G RCP6.0情景下，7月份的径流增加速率为1.77 m3/(s·a)，GFDL_ESM2M RCP8.5情景下，6月份的径流增加速率为2.95 m3/(s·a)。

4 结 语

本文应用贝叶斯神经网络构建气候变化条件下的径流降尺度模型，预测未来气候情景下的径流，定量估计预测结果的不确定性，为解决资料缺乏地区在气候变化条件下的径流预测问题提供科学依据，基本结论为:

(1)与一般的人工神经网络降尺度模型相比，贝叶斯神经网络降尺度模型对叶尔羌河卡群站月平均径流的降尺度效果是较优的，其相关系数达到0.9以上，效率系数达到0.8；其90%不确定性区间对观测径流的覆盖度达到90%以上，区间上下值关于观测值对称性较优，故可以用贝叶斯神经网络对卡群站在未来气候情景下的径流进行预测。

(2) GFDL_ESM2G，GFDL_ESM2M及MIROC5三种模式,RCP4.5, RCP 6.0, RCP 8.5三种情景下,叶尔羌河卡群站未来3个时段( 2020年代,2050年代,2080年代)的年径流受气温升高影响随时间推移呈现增加的趋势，增加幅度为75%～92%，83%～110%，88%～127%，其中RCP8.5情景下的径流增加趋势比其他情景较为明显；不同月份的径流变化存在不同程度的增加趋势,其中9-4月份月径流变化趋势相对不明显，而5-8月份变化趋势较明显。

□

[1] Cannon A J，Whitfield P H．Downscaling recent streamflow conditions in British Columbia Canada using ensemble neural network models [J]．Journal of Hydrology，2002，259 (1-4)：136-151．

[2] Ghosh S，Mujumdar P P．Statistical downscaling of GCM simulations to streamflow using relevance vector machine [J]．Advances in Water Resources，2008，31(1)：132-146．

[3] Kingston G B et al．Bayesian training of artificial neural networks used for water resources modeling [J]．Water Resources Research，2005，41(12)．

[4] Xuesong Zhang, Faming Liang et al．Estimating uncertainty of streamflow simulation using Bayesian neural networks [J]． Water Resources Research，2009，45．

[5] 胡江林，张礼平，宇如聪．神经网络模型预报湖北汛期降水量的应用研究[J]．气象学报，2001，59 (6)：776-783．

[6] Liang F．Bayesian neural networks for non-linear time series forecasting[J]．Statistics and Computing，2005，15：13- 29．

[7] 张贤芳，舒 强，李 偲．叶尔羌河近48年来径流演变规律研究[J]．干旱区资源与环境，2012，26(1)：93-97．

[8] 吴 晶．气候模式对中国西北干旱区气温和降水模拟结果评价[D]．乌鲁木齐：中国科学院研究新疆地理与生态研究所，2013．