基于分形理论的多孔介质渗透破坏研究
王 宇,王士军,谷艳昌(1.南京水利科学研究院,南京 210029;2.水利部大坝安全管理中心,南京 210029;3.河海大学 土木与交通学院,南京 210029)
Mandelbrot创建并发展的分形(fractal)是研究一些具有自相似性的不规则曲线或位形,提出了分维是定量描述这种自相似性的参数[1]。Hausdorff认为维数可以是分数即分数维,并定义了Hausdorff测度[2]。Mandelbrot为模拟分形推广了Hausdorff维数定义,提出分形是一个集合,分形集具有3个特征:①具有任意小尺度下的比例细节或精细结构;②具有某种自相似形式,可以是近似自相似或统计自相似;③分形集的分形维数严格大于它相应的拓扑维数。目前分形几何理论已广泛应用于物理学、化学、地学、生物学、材料学、经济学以及书法艺术等众多领域。
土石坝是由散体粒子、胶结物质和大量各种不同阶次、不规则分布的孔隙、薄弱夹层等构成,是一种结构高度复杂的孔隙体。组成上,土体具有非连续、非均质和不规则性;空间结构上,具有随机分布的多孔隙性;物理力学性质上,呈现非弹性、随机性、各向异性、时间效应和地质环境依赖性[3]。岩土介质的孔隙几何从原子尺度到晶粒尺寸范围内均表现出分形特征,作为一个颗粒群或系统,岩土介质内部结构的渗透破坏具有规律性。因此可以在分形空间中考虑并建立渗透破坏行为的物理指标和运算法则。
目前关于土体渗透变形的理论研究多集中于单个颗粒或者颗粒组的力学平衡上,缺乏对土体颗粒系统性的认识[4]。考虑到分形可以较为准确的揭示非线性动力系统的规律性,将分形理论引入渗透变形的研究中来,试探性地开展了多孔介质渗透破坏的分形特征研究。
1 多孔介质分形几何理论
1.1 多孔介质分形模型
多孔介质可看成更精细粒子的破碎,也用表面积和粒子尺寸分布来表征。谢和平等(1992年)研究了在不同磨碎机理下精细粒子的分形特征,发现粒子尺寸分布的分维D和粒子表面分维Ds都与磨碎机理及样本材料性质相关[5]。根据数目分布函数Yn(x)的定义,尺度在x和x+dx之间的粒子数目dN为:
dN=NtdYn(x)
(1)
式中:Nt为系统总粒子数;Yn(x)为小于尺寸 的粒子总数与系统总粒子数的比值。在这个尺寸区间粒子体积dV可由dN与单一粒子体积的乘积来求得:
dV=Kvx3NtdYn(x)
(2)
式中:Kv为体积形状因子,dV也可由体积分布函数Yv(x)来表示:
dV=VtdYv(x)
(3)
式中:Vt为系统粒子总体积,由式(2)和(3)得:
dYv(x)=Nt(Kv/Vt)x3dYn(x)
(4)
根据数目分布函数的基本定义,Yn(x)可表达为:
Yn(x)=(Nt-N)/Nt%=(1-N/Nt)%
(5)
式中:N定义为尺寸大于x的粒子数目,由于粒子尺寸分布是分形,则有:
Yn(x)∝-x-DdYn(x)∝x-1-D
(6)
代入式(4),再积分,即可得到:
Yv(x)∝x3-D
(7)
式(7)两边乘以密度即可得到质量分布函数的分形表示。应当注意,物体分形往往具有一定的范围,也称无标度区,即当x∈[x1,x2],x1和x2为自相似性存在范围的上下限,上式分形规律成立。
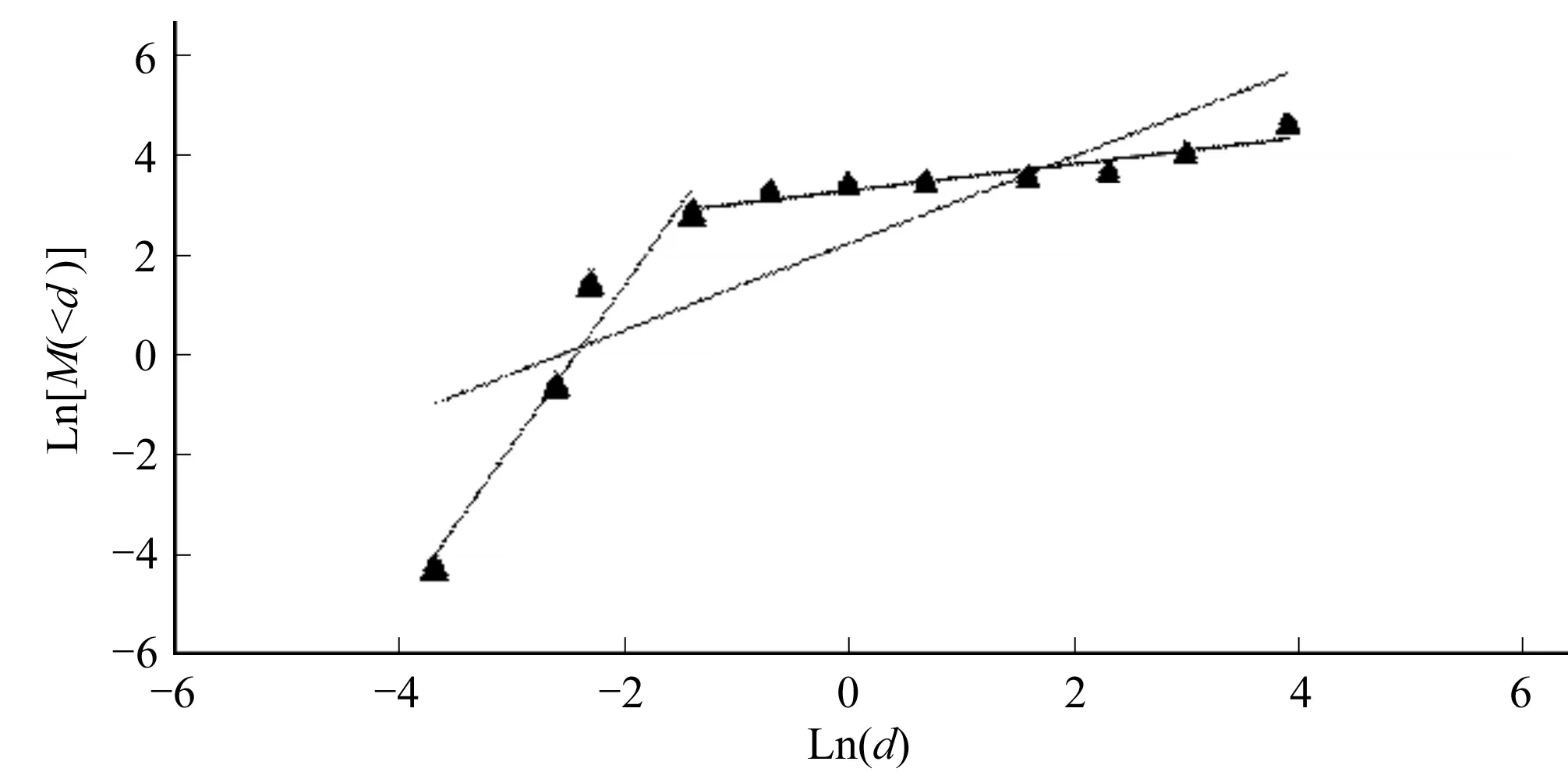
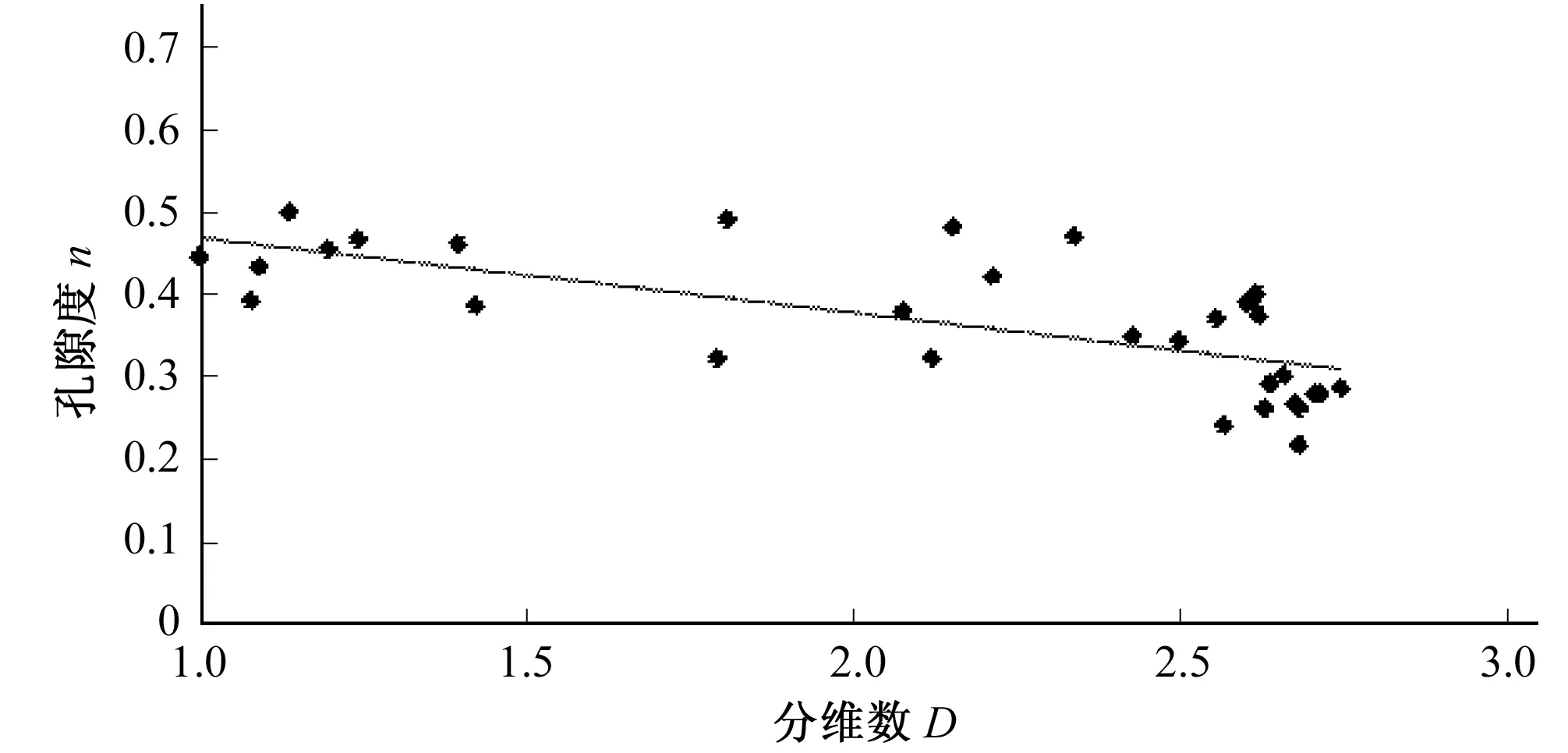
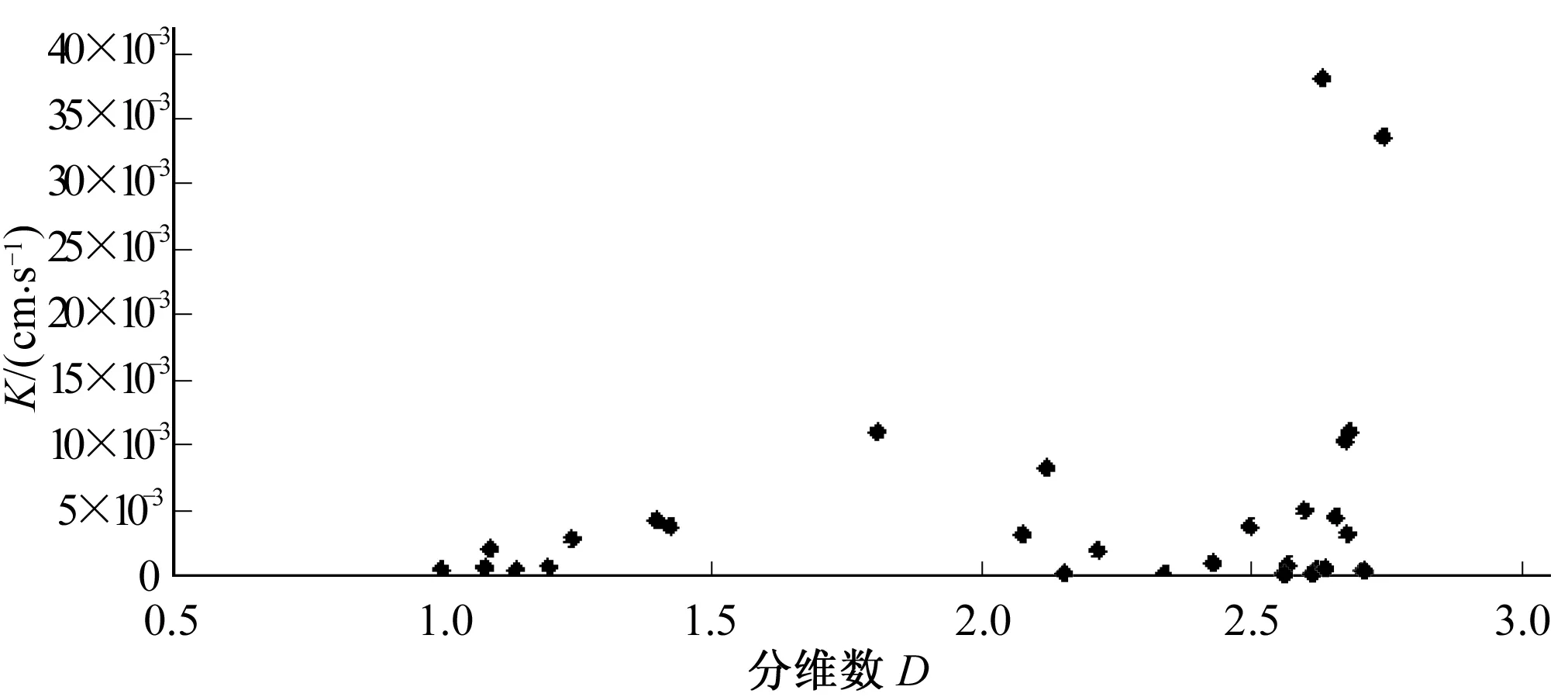
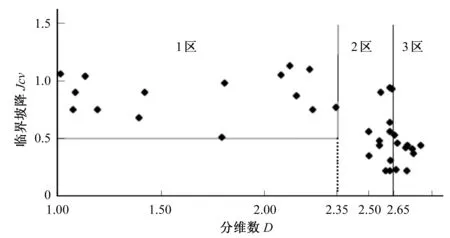
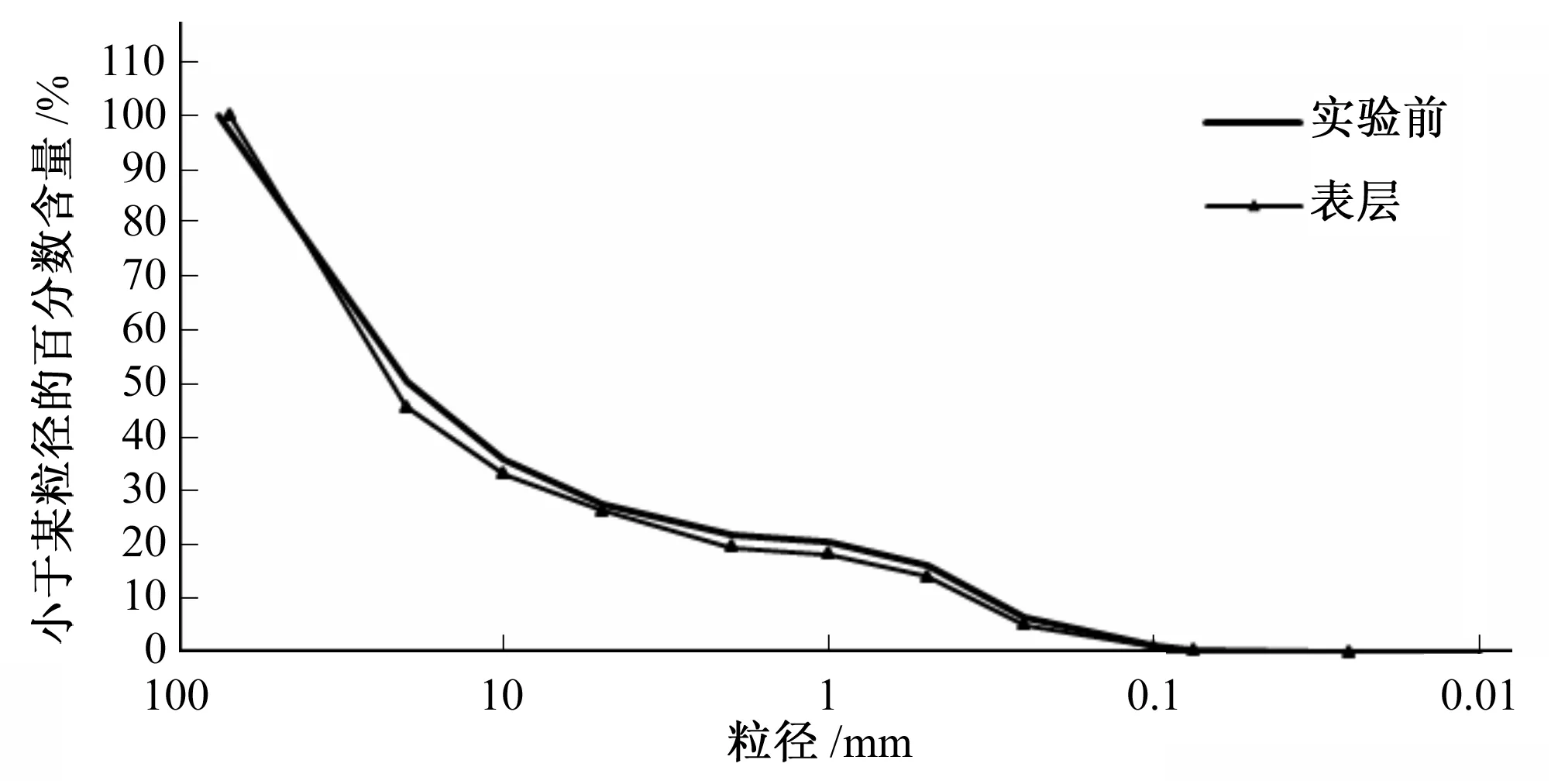
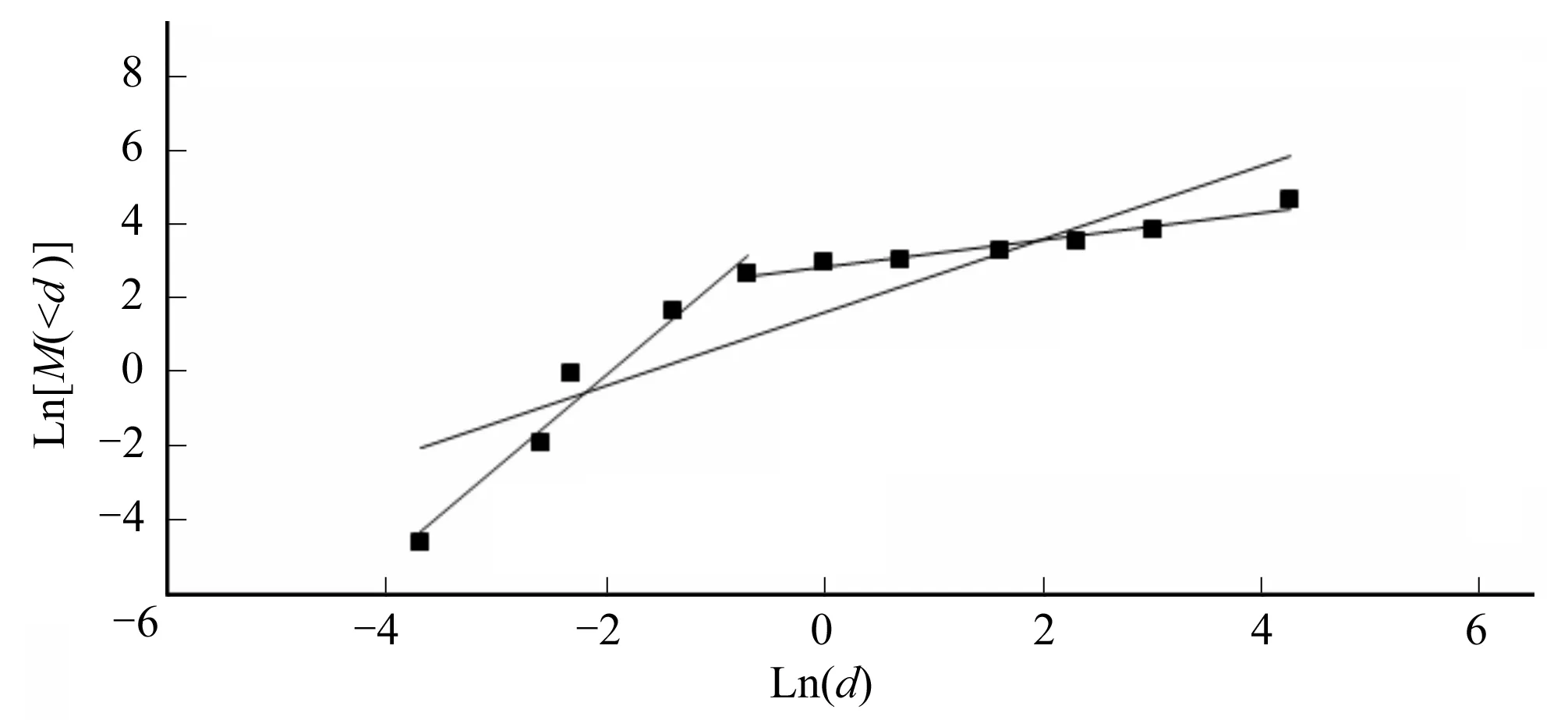
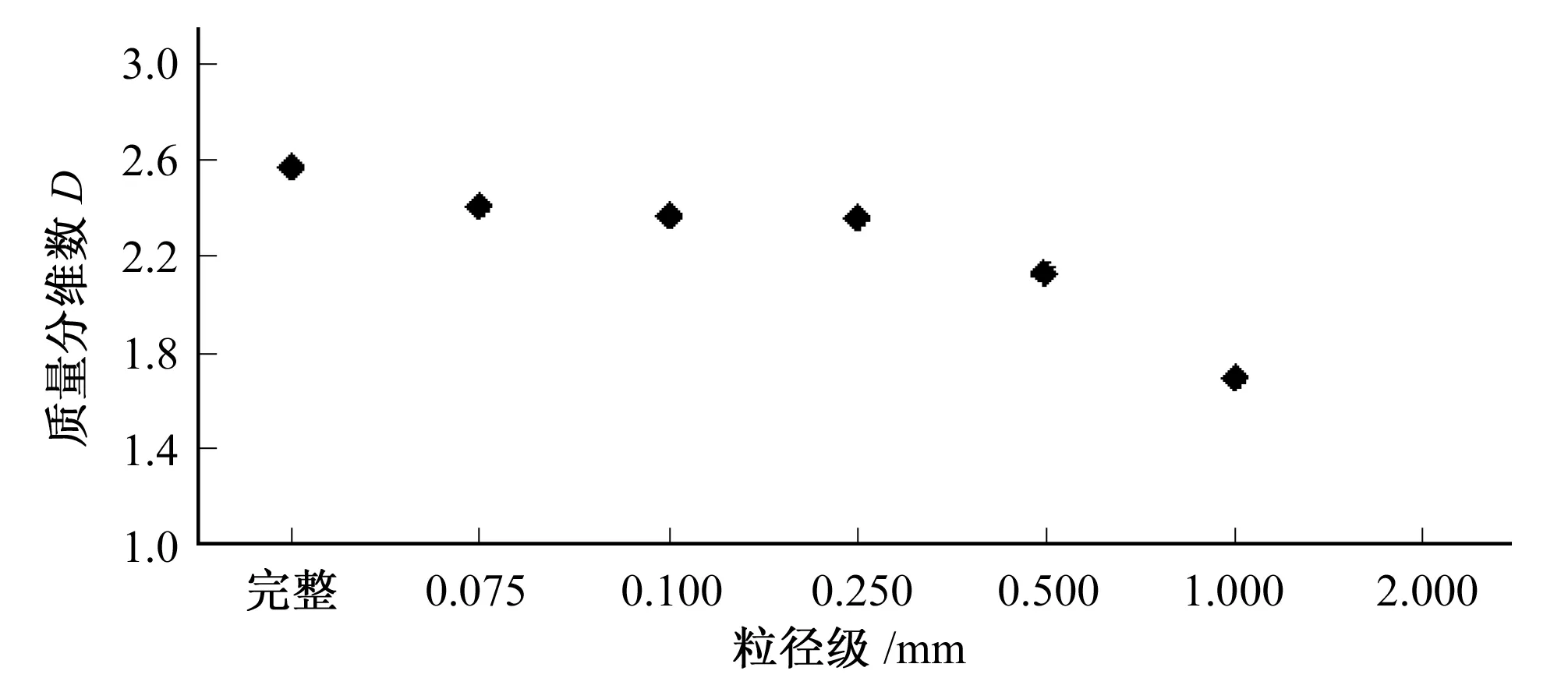
基于多孔介质自相似特点,试验中可利用土样颗分来反映整个土层的级配情况,以及少数土样的物理性质代表整个土层的物理性质,研究多孔介质的质量分维数。土体粒径组成是以小于某一粒径x的土体质量百分含量M( M( (8) 如图1为砂砾石的颗分结果和幂律拟合曲线,其相关系数大于0.99,而且当粒径越小时,拟合程度越高,这正体现了分形存在无标度区。 图1 砂卵砾石的颗分及幂曲线拟合成果Fig.1 Sandy gravels size fitted curve 上述分形模型理论上适用于确定型的分形模型,对于自然条件下统计意义上的自相似分形,因其拓扑结构存在空间差异性,确定型分形模型也有一定的适用性。因此,在岩土介质均匀的情况下,确定型的分形模型能较好的描述土体固相颗粒系统具有幂函数累积数量-尺寸分布关系的分形结构。 在进行分维数计算时,对式(8)两边取对数,对于典型分形而言,小于某粒径的百分含量M( LnM( (9) 其中直线斜率Slope=3-D,则D=3-Slope。根据式(9)可以计算土体的质量分维数,即在已知土体颗分情况下,在双对数坐标轴下绘制质量百分含量和粒径的线性相关曲线,即粒度分布曲线,根据曲线斜率推算分维数。 某砂卵砾石粒度分布曲线如图2所示,相关系数大于0.99,线性关系较好,直线斜率Slope=0.315 6,则D=3-0.315 6=2.684 4。 图2 某砂卵砾石粒度分布曲线Fig.2 Sandy gravels size distribution curve 由于土体结构的不均匀性,可采用多重分形理论来描述具有统计意义的土体质量分形。某土粒度分布曲线如图3所示。若不进行分段统计时,相关系数只有0.666 9,分维数D=2.134 8,可靠性较差。分段统计时,各段拟合度较好,相关系数均大于0.9。此时土体具有两个分维数,需进行分段统计才能准确、完整的描述土体结构特点。对粒径小于0.1 mm进行统计,则D1=3-3.186 6<0,可见土体均匀程度很高,已经不具备分形规律;对粒径大于0.1 mm的土体进行统计,则D2=2.734 6,相关系数大于0.9,可靠性较高。需要指出的是,该土大于0.1 mm的颗粒含量约96%,对土体的稳定性起主控作用,取D=D2=2.734 6是合理的,但此时的质量分维数只能代表大部分土体性质。 图3 某土的粒度分布曲线Fig.3 Soil sizes distribution curve 基于质量分维数的计算方法,理论上对于确定型分形模型质量分维数D∈(2,3),但实际应用中,具有统计意义的分形模型质量分维数D∈(1,2)也是有意义的,这在砂性土、黏性土等比较均匀的细粒料中较常见。 简言之,质量分维数是揭示小于某粒径颗粒累积含量变化规律的重要参数,体现了土体内部结构特征以及与颗粒级配、密实度、渗透性的关系,对土体渗透变形规律有一定的影响。 开展典型级配下多组天然的砂性土、粉质黏土土等主要土石坝材料的渗透破坏物理模拟试验,采用测压管、传感器及电子数据采集系统进行量测,研究土体物理性质、渗透变形及破坏的分形特征。 土体孔隙度随分维数变化情况如图4所示。孔隙度与分维数相关性较好,相关系数R接近0.7;分维数与孔隙度呈反比关系,当D>2时,孔隙度随着分维数增大而减小的规律更明显。分维数表征单位体积下逐级颗粒的积累情况,分维数越大,孔隙度一般越小。 图4 土体分维数和孔隙度的关系Fig.4 Relationship between dimension and porosity 土体不均匀系数随分维数变化情况如图5所示。不均匀系数与分维数之间存在较好的指数关系,相关系数R大于0.7;分维数越大,单位体积土体逐级颗粒质量积累越多,不均匀程度越高。 图5 土体分维数和不均匀系数的关系Fig.5 Relationship between dimension and uneven coefficient 土体中值粒径D50和分维数的关系如图6所示。D50和分维数之间存在较好的二次关系,相关系数R接近0.6;随着分维数的增大,土体D50有增大的趋势。分维数越大,不均匀程度越高,一般颗粒越粗。 图6 土体分维数和中值粒径D50的关系Fig.6 Relationship between dimension and medium size D50 土体干密度和分维数的关系如图7所示。干密度和分维数之间存在较好的二次关系,相关系数R接近0.7;随着分维数的增大,土体干密度有增大的趋势,但是处于同一分区内的土体干密度随分维数增大而增大的规律则不强,主要因为分维数越大,反映出单位体积土体逐级颗粒积累越多,不均匀程度越高,一般颗粒越粗,但对于级配接近的砂砾料或者砂性土而言,干密度的大小和粒径的关系则较弱,干密度大小还受到颗粒排列方式密实情况等的影响。 图7 土体分维数和干密度的关系Fig.7 Relationship between dimension and dry density 土体渗透系数和分维数的关系如图8所示,由图可知,随着分维数D的增大,渗透系数有增大的趋势,这是因为分维数较大,颗粒较粗,渗透性能越强。 图8 土体分维数和渗透系数的关系Fig.8 Relationship between dimension and permeability 分维数D主要反映小于某粒径颗粒累积含量变化规律的参数,和颗粒级配、密实度等都有关系。由分维数的计算方法可知,当分维数较大时,表示小于某粒径颗粒累积含量较少,颗分曲线越平缓,土体有粗化现象。不均匀系数及中值粒径增大,孔隙度减小,干密度也增大,因此质量分维数是表征土体结构情况的参数,对土体渗透变形特性具有一定的影响。 各种典型级配下粉质黏土、砂性土的渗透变形及分维计算结果汇总如图9所示,由图可知,分维数主要为[1,3];流土变形的临界坡降均大于0.5,分维数小于2.35;管涌变形的临界坡降均小于0.5,分维数皆大于2.5;随着分维数增大,土体临界坡降逐渐减小。这是因为分维数越大,土体粒径和干密度较大,不均匀性较高,且渗透系数较大,综合导致土体的临界坡降减小。 图9 土体分维数和临界坡降汇总Fig.9 Soil dimensions and critical gradients 临界坡降和分维数的关系如图10所示,可以分为3个典型区域:1区(D≤2.35)、2区(2.35 图10 土体分维数和临界坡降的关系Fig.10 Relationship between dimensions and critical gradient 不同土体具有不同的分形特征,渗透破坏后的分形特征是否会发生变化以及如何变化也是值得研究的,这对预测堤坝土体是否存在渗流隐患具有重要意义。因此,试验采集各土体渗透破坏前后的颗分情况,开展土体渗透破坏前后分形规律的变化情况研究。 图11为土样渗透破坏前后的颗分情况,试验后分表层、中层、底层三层取样,由图可知,土体渗透破坏后出现了粗化现象;图12为渗透破坏前的粒度分布曲线,分维数D前=3-0.347 4=2.652 6;图13为渗透破坏后表层土样的粒度分布曲线,分维数D后=3-0.374 2=2.625 8;图14为颗粒流试验过程中各阶段土体分维数的变化过程。比较可知,随着土体渗透破坏的逐步发展,质量分维数降低,可见土体出现渗透破坏后, 颗粒中累积的能量会逐步释放。当渗透破坏发展到0.1mm粒径级后,分维数下降较快,这与细颗粒流失后土体趋于均匀有关。因此,可以通过土体出现渗透变形后质量分维数会出现下降的情况,来预测渗透变形的发生和发展情况,从而减少堤坝因渗透破坏而引起的致灾隐患。 图11 土样渗透破坏前后的颗分情况Fig.11 Soil size before and after seepage failure 图12 土样渗透破坏前的粒度分布曲线Fig.12 Soil size distribution curve before seepage failure 图13 土样渗透破坏后表层土的粒度分布曲线Fig.13 Soil size distribution curve after seepage failure 图14 颗粒流试验中各阶段土体分维数的变化过程Fig.14 Soil dimension changing process in particle flowing test 基于分形几何理论,重点研究了土体渗透变形的分形特征,提出了可作为划分渗透变形判别标准的质量分维数,分析了土体渗透变形前后的分形特征。分析认为可通过土体出现渗透变形后质量分维数会出现下降的情况,来预测渗透变形的发生和发展情况,从而减少堤坝因渗透破坏而引起的致灾隐患。 本文仅是对多孔介质渗透破坏的分形特征进行了尝试性研究,仍需要在工程实践中进一步检验和完善。 □ [1] Thevanayagam S, Nesarajah S. Fractal model for flow through saturated soils.[J]. Geotech. and Geoenvir. Engrg., ASCE, 1998,124(1):53-66. [2] Hyslip J P, Vallejo L E. Fractal analysis of the roughness and size distribution of granular materials[J], Engineering Geology, 1997,48(3-4):231-244. [3] 谢和平. 岩土介质的分形孔隙和分形粒子[J]. 力学进展. 1993,23(2):145-147. [4] 杨 超. 堤坝渗透破坏过程物理模拟试验及机理研究[D]. 南京:南京水利科学研究院,2012:53-61. [5] 谢和平, 鞠 杨. 分数维空间中的损伤力学研究初探[J]. 力学进展,1999,31(3):300-305.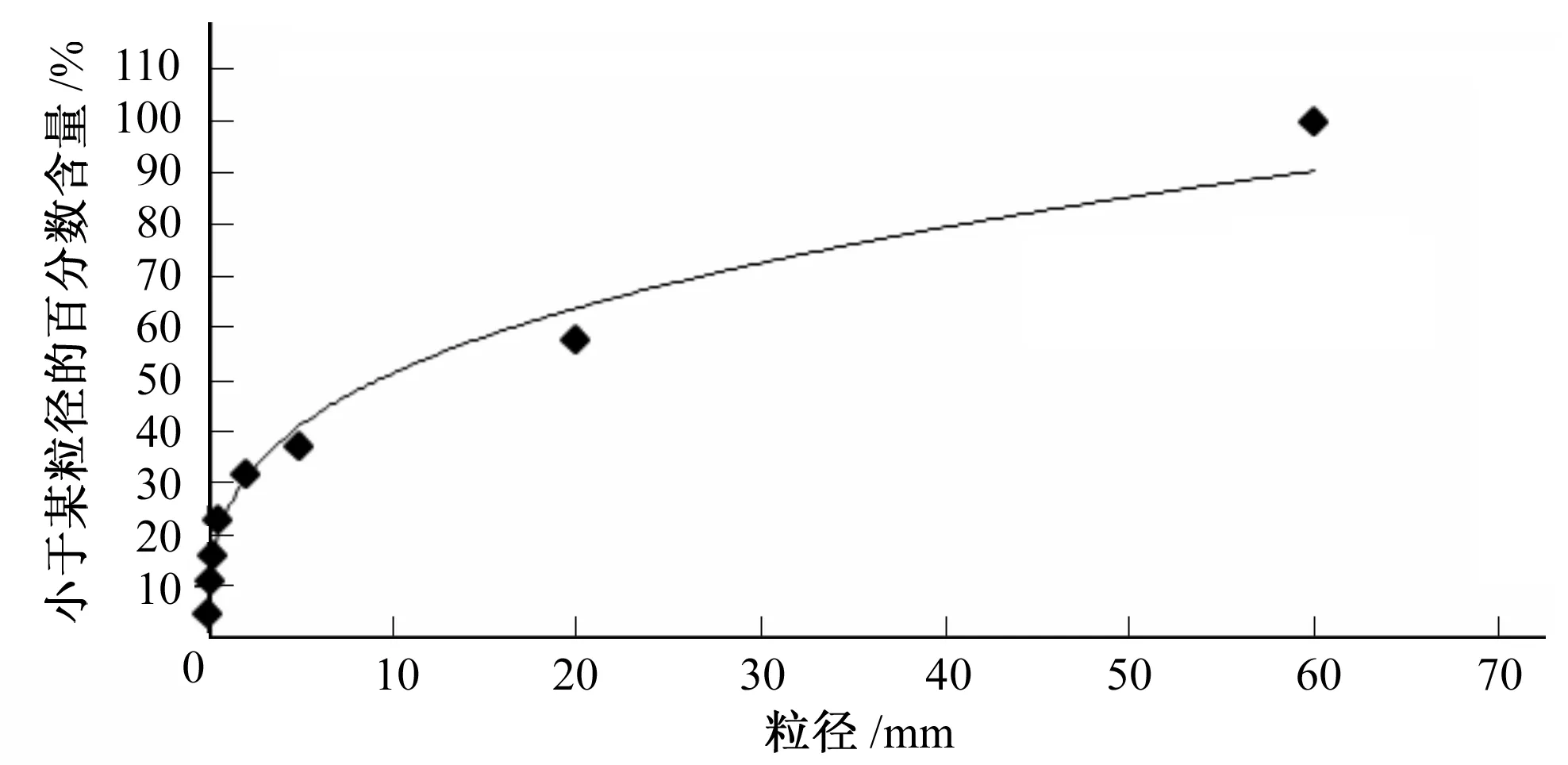
1.2 质量分维数的计算

2 土体渗透破坏分形特征分析
2.1 物理性质分形特征



2.2 渗透变形分形特征

2.3 渗透破坏过程分形特征

3 结 语

