微段时间波浪力计算法在柔性浮式防撞系统上的应用

于 伟，陈徐均，施 杰，刘俊谊

（解放军理工大学 野战工程学院，江苏 南京 210007）



微段时间波浪力计算法在柔性浮式防撞系统上的应用

于 伟，陈徐均，施 杰，刘俊谊

（解放军理工大学 野战工程学院，江苏 南京 210007）

摘要：为了研究波浪力对于柔性浮式防撞系统拦阻效能的影响，本文提出了分步处理波浪力的方法，进行了撞击过程的模拟计算研究。文中基于势流理论运用ansys_aqwa软件，求得了不同波浪入射角及不同相位下结构物的波浪力。在模拟船舶撞击系统的过程中，将计算较为复杂的波浪力，转化为运用处理不同时刻波浪入射角和相位角的问题进行连续分析计算。研究表明，微段时间波浪力计算方法可以用于柔性浮式防撞系统的运动分析，船舶撞击过程中不能忽略波浪力的影响。

关键词：波浪力；势流理论；柔性浮式防撞系统

引 言

波浪力的计算工作开始得比较早[1,2]，方法也比较多[3,4]，国内外对于锚泊系统的在波浪中动力响应问题[5~7]的研究已经十分的深入。M. Yanga[8]用泰勒展开法处理边界条件，在时域上处理了波浪影响下的水动力相应问题。Hiroshi[9]研究了波浪力对于水下浮式隧道的影响。丁军等人[10]基于有限水深格林函数、Morison公式和时域耦合动力分析方法，分析了传统系泊方式和桩柱式系泊方式下平台的运动和系泊系统动力响应。乔东生等[11]利用单根锚泊线由于上部浮体运动而产生的能量耗散原理计算锚泊阻尼。

通常锚泊系统在锚泊作用下，波浪中仅限于微幅的振动和漂移，在考虑走锚的条件下，锚泊系统会出现大幅运动的状况。吴广怀[12]等人设计了由多个锚泊浮体结构相连构成的走锚消能式柔性防船舶碰撞系统，需要对大幅运动的锚泊系统在波浪中的运动进行研究。陈徐均[13~15]等人运用数值模拟撞击过程的方法，分析了走锚消能设施的运动过程以及能量的转换关系。本文在陈徐均等人分析研究的基础上，运用微段时间波浪力计算方法，加入了波浪力对于碰撞过程影响的考虑。

1 柔性浮式防撞系统简介

柔性浮式防撞系统的工作是通过水面拦阻系统拦挡碰撞船舶，主要是以浮筒与碰撞船舶直接接触的方式承载碰撞能量，然后通过缆索链进行力和能量的传递。柔性浮式防撞系统由两大部分组成：水面拦阻系统（上部结构）和锚碇系统（水下结构）。水面拦阻系统由浮式结构和缆索链组成，浮式结构间通过柔性缆索链连接；锚碇系统由锚链和锚组成，锚链的上链端固定于水面拦阻系统的缆索链上。图1是柔性浮式防撞系统的示意，图1（b）中各部件并不在同一平面内，其中锚位于水底，图中用小正方形表示；而浮筒浮于水面，图中以较大长方形表示。

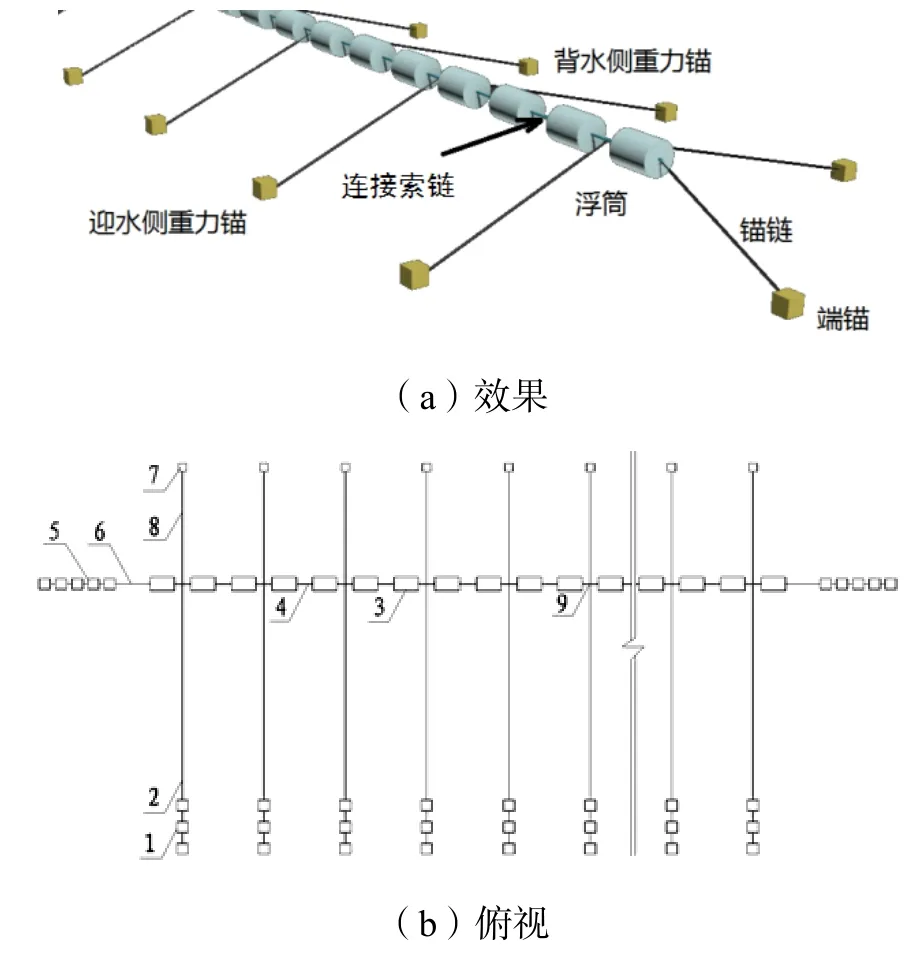
1.锚一 2.锚链一 3.浮筒 4.缆索链 5.端部锚6.端部锚链 7.锚二 8.锚链二 9.索链交点图1 柔性浮式防撞系统示意

柔性浮式防撞系统主要以走锚消能的方式，使撞击船舶的能量逐渐减小，最终拦停船舶，达到防止船舶进一步撞击桥梁的目的。在船舶撞击防撞系统的过程中，船舶撞击系统的水面拦阻系统，通过缆索链的受力传递，使得整个系统在撞击力及其他外力的作用下发生运动。在船舶撞击的过程中，波浪力会直接影响船舶以及系统浮筒的受力状态，波浪以环境能量的形式影响系统的能量转换，从而影响拦阻系统的工作效能，所以波浪力对拦阻系统影响的研究十分必要。

2 波浪力计算理论

通常计算波浪力有2种方法，远场积分方法和近场积分方法。近场积分法是基于势流假定，在物体表面直接对压力进行积分计算得到波浪力。远场积分法是基于动量和能量守恒求得波浪力。本文运用近场积分法分析波浪力对撞击过程的影响。假设流体为均匀、无粘性和不可压缩的理想流体，浮体的特征尺度与波长是同一量级的，波幅远小于浮体的特征尺度且重力是唯一的质量力。在理想流体的流场中，连续性方程和欧拉运动方程可表示为：

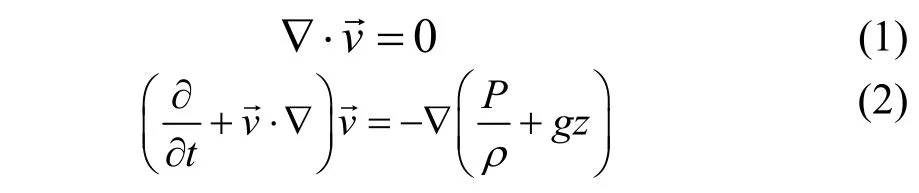
利用无旋条件及速度与速度势的关系，整理式(2)并进行积分可以得到：

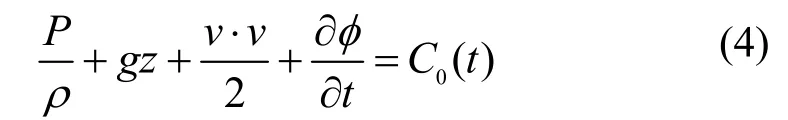
式中，C0( t )为待定的时间t的函数。

对于无旋的理想流体，控制流体的基本方程为式(3)和式(4)，式(3)决定流场中速度的分布，式(4)决定流场中压力的分布，只要求解出流场中的速度势ø，就可根据式(4)求得整个流场的压力分布，进而确定浮体受到的流体作用力。

求解式(3)需要一定的边界条件，这些边界条件包括：

物面条件：

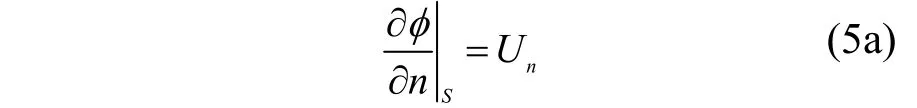
运动学条件：

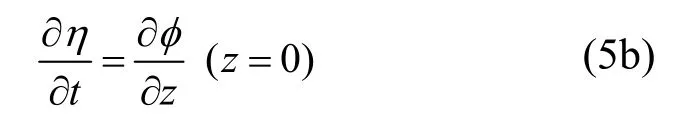
动力学条件：

无限远处辐射条件：

海底边界条件：

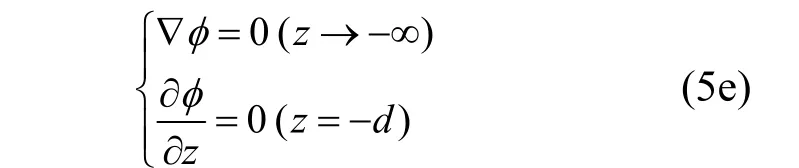
若使用的波浪理论为一阶，可在流体区域内应用叠加原理把速度势分解，定义流场内的速度势为：

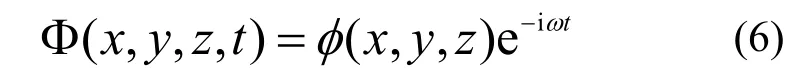
单位波幅引起的波浪总速度势可表示为：

求得场内的速度势后，航速为U0的物体上的波浪力为：

3 计算模型

本文采用如图1所示的计算实物模型，实物模型根据试验模型按相似原则的理论，以一定缩尺比放大得到。柔性浮式防撞系统的工作环境为9 m水深，水流流速为2.26 m/s，船舶为7500 t，长115.0 m，宽17.6 m，型深8.80 m，满载吃水6.60 m。重力锚采用单个或多个串联的等质量钢筋混凝土块，每个钢筋混凝土块与水底的最大摩擦力和动摩擦力都为640 kN。迎水侧由3个钢筋混凝土块串联构成，背水侧由单个钢筋混凝土块构成，两端由10个钢筋混凝土块串联构成。浮筒采用钢材制成的空心圆柱体，浮筒长4.8 m，直径4.8 m，吃水深度2 m。连接索链和锚链采用同样的索链，索链的有效面积为3.66 cm2，弹性模量为2.1×1011Pa，各类索链的有效长度参数如表1。

表1 索链参数

在船舶撞击柔性浮式防撞系统过程中，波浪力对撞击船舶和系统浮筒有一定的影响。由于各种外荷载的综合作用比较复杂，船舶上的作用力的大小、方向、作用点也会实时的发生改变，所以船舶在此过程中的运动姿态也会实时的发生改变。为了研究问题的简单，假定船舶在撞击拦阻系统的过程中，船舶撞击运动的姿态不会发生改变，即波浪入射角与船舶纵轴线的夹角始终不变。虽然在撞击过程中，浮筒的漂浮状态可能有所改变，即浮筒会在水平面中上下浮动，但浮动的幅度相对于整个系统来讲可以忽略不计。可以将浮筒的受力简化在二维平面内，忽略其受到的重力和浮力的作用。基于ansys软件，本文建立的浮筒以及船舶的波浪力计算模型如图2所示。

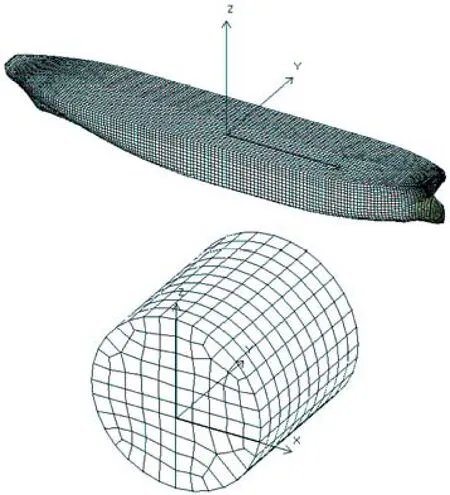
图2 船舶和浮筒网格划分模型

4 波浪力计算方法分析

在分析计算的过程中，分别考虑周期为3 s和5 s的斯托克斯波浪，波高均为0.5 m，在水深为9 m的环境中，求得周期为3 s的波浪的波长为13.8 m；周期为5 s的波浪的波长为34.2 m。波浪的传播方向与船舶撞击方向相同。

波浪力的时域分析较为复杂，流场的变化以及结构物运动等等问题难以综合考虑，而撞击过程需要对复杂的系统进行时域分析。为了简化波浪力的时域计算方法，将波浪的连续作用视为是不同时刻微段内波浪力的作用，这样就可以将波浪力的求解简化。运用力学及运动学基本原理，将时间微段连续化，就可以分析整个的撞击过程。

时间微段连续化过程中，需要考虑结构物运动的连续性以及波浪运动的连续性。对于规则波浪，影响其作用在结构物上的力主要有2部分：1）波浪的传播方向，即波浪传播方向与结构物的位置关系；2）波浪的相位差，特别是波长较长的波浪，波浪相位差的影响更为明显。

波浪传播方向对于波浪作用力的影响，主要是指波浪的入射波与结构物的相对夹角，在柔性浮式防撞系统的计算模型中浮筒纵轴与波浪的夹角，以及船舶的纵轴线与波浪入射的夹角，都会影响波浪对于柔性浮式防撞系统的波浪力。在船舶撞击系统的过程中，假设了船舶不会在外力的状况下发生转动，所以波浪入射波与船舶纵轴线的夹角始终不变。系统中的浮筒或浮式结构物，会随着撞击的进行，改变自身的位置和角度，波浪的入射角不变，入射波与浮筒纵轴的夹角就会随碰撞发生变化。不同时刻，入射波与浮筒纵轴会有不同的夹角，根据浮筒的运动就可以求得每个时间微段内夹角大小。

对于波浪作用力在结构物（以浮筒为例）所在位置的相位差，由2部分组成：1）由于浮筒运动，浮筒位移的改变引起的相位差；2）在浮筒运动过程中，波浪本身随时间向前运动引起的相位差。在考虑相位差的过程中，应当将两类原因综合考虑，可以得到浮筒在不同时刻不同位置的综合相位差。假设浮筒运动时间后，运动的距离为，波浪的周期为，波长为，则相位差的大小可以表示为：

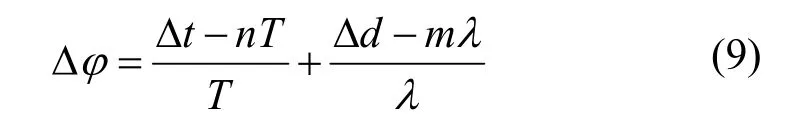
式中：n为相差的周期数；m为相差的波长数。

图3为计算波浪相位差的示意，黑色线条表示波浪和浮筒的初始位置，红色线条表示一段时间后波浪和浮筒的位置，为时间内波浪波形的传播距离。

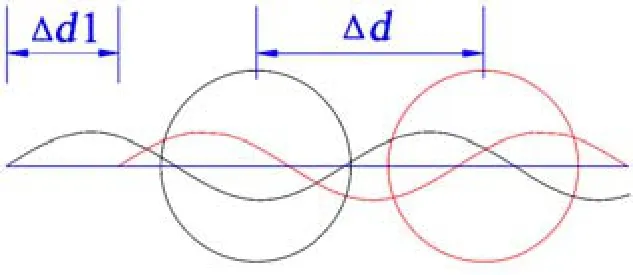
图3 计算波浪相位差示意

在求解波浪力时，运用势流理论为基础的ansysaqwa软件。运用软件可以求出单个浮筒在一定方向的斯托克斯波浪作用下的波浪力的相关参数。由于考虑系统浮筒在二维平面内的运动过程，即忽略了引起浮筒的垂荡、横摇、纵摇运动的3种性质的波浪力。分别将引起浮筒横荡、纵荡、首尾摇运动的力，按照入射波浪的方向、波高、频率为依据，图4~图5列出波浪周期差、浮筒倾斜角度与3种波浪力分量之间的大小关系。图4~图5中，x轴坐标为波浪的周期差值，y轴坐标浮筒为受到的波浪力或弯矩，z轴坐标为浮筒纵轴与入射波浪的夹角。对于船舶受到的波浪力，仅考虑不同相位角对于横荡运动的影响，波浪相位角与船舶受力关系如图6~ 图7。波浪的初始相位角为0°。

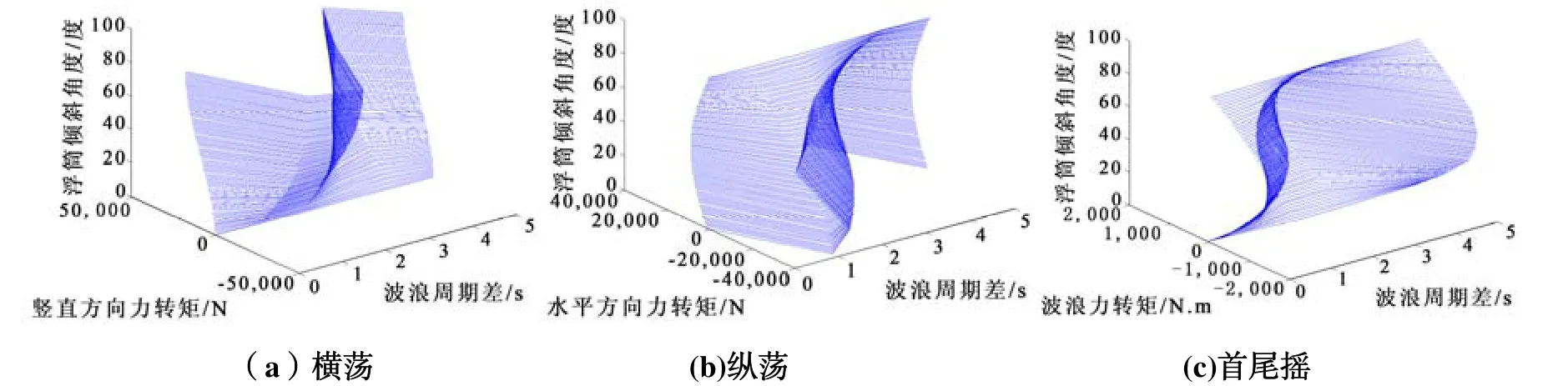
图4 浮筒上两个方向波浪分力及转矩（T=5 s）

图5 浮筒上两个方向波浪分力及转矩（T=3 s）

图6 船舶波浪力(T=5 s)

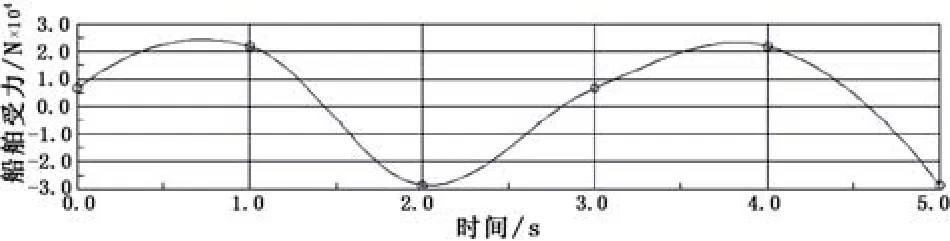
图7 船舶波浪力(T=3 s)

在确定了波浪的初始条件下，如果已知浮筒（船舶）轴线与原始位置轴线的夹角和浮筒（船舶）所在位置与原始位置的相位差，就可以确定浮筒（船舶）在该位置、该姿态下的受力状况，根据时间进程处理波浪力的作用，用于系统运动过程的计算。

5 计算结果与数据分析

分别计算无波浪力作用和周期为3 s、5 s波浪作用下船舶撞击柔性浮式防撞系统的过程。用数值模拟运动的方法，得到当船舶停止运动后，系统最终的姿态如图8。图中矩形代表浮筒，细线代表连接索链或锚链，星号代表上下游的重力锚，圆圈表示两端的重力锚。在无波浪的工况下用蓝色线条标记，在周期为3 s的波浪的作用下用红色线条标记，在波浪周期为5 s的波浪的作用下用黑色线条标记。

从图8中，特别是图8（b）上部结构的姿态看出，周期为3 s的波浪作用下，系统的最终形状与无波浪工况的形状基本相同，这说明周期为3 s、波高为0.5 m的波浪对于系统运动的影响不大。而对于周期为5 s、波高为0.5 m的波浪作用，从图中能够明显看到系统上部结构的漂移距离与船舶的漂移距离都比前两种工况要大。特别是在靠近端锚的两个锚碇交叉点的3个浮筒的姿态，呈现出略微的弧线形状，说明周期为5 s波浪对于系统的上部结构有明显的影响作用。

图8 系统撞击后姿态对比

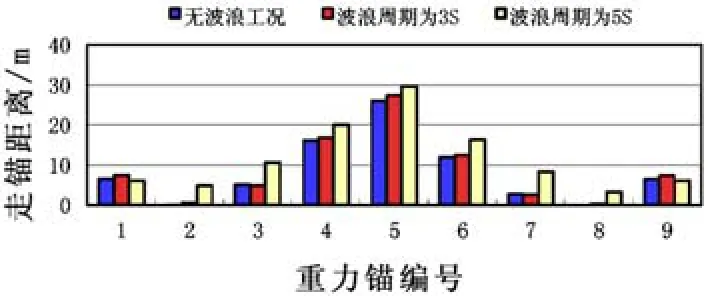
图9 重力锚的走锚距离的比较示意

图9为船舶撞击拦阻系统几种工况下重力锚的走锚距离的比较示意，从图中看出，不考虑两侧的端锚，从2号重力锚至8号重力锚，有波浪作用时重力锚的走锚距离较大；长周期大波长的波浪比短周期小波长的波浪的工况下，走锚距离要大。尽管波浪是周期性往复的作用力作用于碰撞过程，但是总体上，如果碰撞船舶与波浪的传播方向相同，波浪对于碰撞船舶与系统上部结构有推动作用，会影响拦阻系统的效能。

对于两侧的端锚，出现了长周期大波长的波浪影响下，走锚距离更小的状况。对于1号重力锚，将重量锚在不同工况下最终的位置标记如图10。原始端锚点坐标（-52,0），无波浪工况下最终端锚位置（-45.352 2，0.006 8），在周期为3 s波浪作用下最终端锚位置（-44.499 6，0.054 6），在周期为5 s波浪作用下最终端锚位置（-45.901 4，0.150 2）。

图10 不同工况1号端锚位置示意

尽管在周期5 s波浪的作用下，端锚滑移的绝对距离较小，但是，在船舶运动方向上移动的距离较其他两种工况要大的多，而且绝对距离小的程度有限。在模拟船舶撞击过程中，是通过时间微段进行分段的计算，波浪力在每一步时间微段上主要影响了端锚在船舶运动方向的滑移距离。所以尽管在周期5 s波浪的作用下，端锚滑移的绝对距离小，结果也是合理的。在每个微段时间的计算过程中，波浪力的能量更多的消耗在2号重力锚至8号重力锚的走锚耗能上，使得最终出现这样的结果。

6 结 论

本文运用时间微段的方法处理了作用在柔性浮式防撞系统上的波浪力，通过计算分析，比较了几种浅水波浪工况下的结果。研究表明：

1）时间微段处理波浪力时，对于不同性质的波浪，仅需要考虑波浪的入射角度以及不同时间微段上波浪作用的相位差。

2）波浪力对结构物的影响与波浪与结构物的相对尺寸相关，计算结果中波浪对于船舶的影响要大于对拦阻系统上部结构的影响。

3）能量相对较小的波浪对结构物影响效果不大，波浪周期为3 s的短波长波浪的影响效果，要小于波浪周期为5 s的长波长波浪。

总体而言，时间微段处理波浪力的方法能够分析波浪力对于结构物的影响效果，是分析柔性浮式防撞系统防撞的简单有效的方法。

参考文献：

[1] Hajime Maruo. The Drift of a Body Floating on Waves[J].Journal of Ship Research, 1960, 4: 1-10.

[2] Joosen W P A. Slender-body theory for an oscillating ship at forward speed[J]. 5th Symposium on Naval Hydrodynamics, 1964: 167-183.

[3] Eatock Taylor R, Chau F P. Wave diffraction theory-some developments in linear and nonlinear theory[J]. Journal of Offshore Mechanics and Arctic Engineering, 1992, 114: 185-194.

[4] Cong P W, Gou Y, Teng B. A new approach to low-frequency QTF and its application in predicting slow drift force [J]. Ocean Engineering, 2012, 53: 25-37.

[5] Huang S. Dynamic Analysis of Three-Dimensional Marine Cables[J]. Ocean Engineering, 1994, 6(21): 587-605.

[6] A P Shashikala, R Sundaravadivelu, C GanaPathy. Dynamic of A Moored Barge under Regular and Random Waves[J]. Ocean Engineering, 1997, 5(40): 401-430.

[7] Jason I Gobat, Mark A Grosenbaugh. A Simple Model for Heave-induced Dynamic Tension in Catenary Moorings[J]. Applied Ocean Research, 2001, 23: 159-174.

[8] M Yanga, B Tenga, D Ninga, et al. Coupled dynamic analysis for wave interaction with a truss spar and its mooring line/riser system in time domain[J]. Ocean Engineering, 2012, 39: 72-87.

[9] Hiroshi Kunisu. Evaluation of wave force acting on Submerged Floating Tunnels[J]. Procedia Engineering, 2010, 4: 99-105.

[10] 丁军, 程小明, 田超, 等. 近岛礁浅水环境下浮式平台系泊系统设计研究[J]. 船舶力学, 2015, 19(7): 782-790.

[11] 乔东生, 樊天慧, 欧进萍. 不同类型锚泊方式对深水浮式平台的阻尼贡献比较计算[J]. 船舶力学, 2014, 18(5): 507-515.

[12] 吴广怀, 于群力, 陈徐均. 非通航孔桥的大距离走锚消能式防撞系统[J]. 公路, 2009, (1): 213-218.

[13] 陈徐均, 黄光远, 吴广怀. 船舶撞击锚泊防撞系统的能量平衡关系分析[J]. 解放军理工大学学报（自然科学版）, 2009, 10(1): 71-76.

[14] 陈徐均, 黄光远, 吴广怀. 柔性浮式系统受撞后运动的算法及其收敛性[J]. 解放军理工大学学报（自然科学版）, 2011, 12(5): 501-506.

[15] Chen X J, Huang G Y, Wu G H, et al. New numerical method for flexible floating collision-prevention system and its convergency discussion[J]. Journal of PLA University of Science and Technology (Natural Science Edition), 2011, 12(5): 501-506.

[16] Chen X J, Huang G Y, Wu G H, et al. Numerical simulation for the motion of the flexible floating collision-prevention system[J]. Journal of Offshore Mechanics and Arctic Engineering, 2013, 135:1-9.

Application of Micro-time Wave Force Calculation in Flexible Floating Collision-avoidance System

Yu Wei, Chen Xujun, Shi Jie, Liu Junyi
（Academy of Field Engineering, PLA University of Science and Technology, Nanjing Jiangsu 210007, China）

Abstract:In order to study the wave force for effect of The Flexible Floating Collision-Prevention System (FFSCS), step by step computational method of the wave force is presented in this paper, numerical simulation is carried out for the collision process. Based on potential flow theory, the ansys_aqwa software is used to obtain the wave forces of different incident angles and different phase angles. In the process of simulation of the ship collision, the calculation of the wave force is more complex. This paper use the method, which deal with different wave incident angles and different wave phase angles at Micro times, to calculate continuously. Comparative analysis of the results show that, the effect of different waves for the collision process is different. In the collision process, the influence of the wave force can’t be neglected.

Key words:wave force; potential flow theory; flexible floating collision-avoidance system

作者简介：于伟（1982-），男，博士，研究方向为浮桥设计理论及关键技术。

基金项目：国家自然科学基金资助项目（51379213）；国家科技支撑计划课题（2014BAB16B05）；工信部高性能船舶科研资助项目[工信部联装（2012）533号文]

收稿日期：2015-10-19

DOI:10.16403/j.cnki.ggjs20160101

中图分类号：U653.2

文献标识码：A

文章编号：1004-9592（2016）01-0001-06