深挖式蓄水池的挖深优化设计模型

陈晓俊，王文君，吴英杰，王玉川，全 强，周泉成，尹 航(.水利部牧区水利科学研究所，呼和浩特0000；.西北农林科技大学，陕西 杨凌 700)

近年来内蒙古、新疆等西北干旱地区新建了大量露天煤矿。煤炭开采前需把地下水水位降到煤层标高以下，目前主要采用疏干方式来降低地下水位，而疏干降水过程中会产生大量的疏干水，因此为了提高疏干水的水资源利用，很多地处平原的煤矿在煤矿开采初期建设储藏疏干水的蓄水池，为后期煤矿配套园区工业用水及排土场道路降尘、排土场复垦绿化、生产建设及生活等用水提供保证，对露天矿的可持续绿色发展意义深远。本文以深挖式蓄水池为研究对象，通过分析蓄水池建设和运行成本与挖深的关系，建立蓄水池挖深优化模型，得出蓄水池最优挖深，以期为类似条件下的蓄水池设计提供参考。

1 蓄水池挖深优化模型建立

露天煤矿蓄水池建设的主要目的是为后期工业及配套设施供水，因此蓄水池的挖深优化，直接关系到工程投资大小和投资效益，而判断挖深优化与否，主要看在设计使用年限内平均单位体积供水成本的高低。根据分析研究可知，蓄水池的挖深H不仅直接决定了其固定资产等费用，也间接影响建成后的运行费用等，因此选择蓄水池挖深H为决策变量，模型以蓄水池平均单位供水成本最低为目标函数，将筑坝费用、护坡费用、征地费用、引、供水费用、蒸发损失等与挖深H建立函数关系，最终建立以挖深H为决策变量的单目标优化模型。

1.1 基本假设

为了简化目标函数，通过分析研究，本文模型建立基于如下几个假设。①为节约占地压煤，假设蓄水池蓄水部分主要位于地面以下，挖深H即为地面以下深度，地面以上围坝高只为超高，且围坝总的平面布置是闭合的，坝高处处相等。②蓄水池平面形状假设为正方形或圆形。③蓄水池主要为深挖，征地面积及费率对挖深影响很小，因此不考虑征地部分投资。④单位坝长造价与坝的断面积A成线性关系，所用土料均一，沿坝轴线方向内、外边坡比不变。⑤蓄水池土方开挖单价为考虑土类、运距及开挖方法等因素的一个综合单价，填筑单价为考虑碾、压夯实等因素的一个综合单价。⑥当H≥10时自动设马道，马道设于0.5H处。

1.2 建设费用组成

蓄水池建设及运行期间的投资 ，主要包括以下7个部分[1]：①固定资产I1及其折旧费I′1，其中固定资产包括围坝填筑费用I11、护坡费用I12、防渗费用I13和土方开挖费用I14；②蓄水池征地补偿费I2，根据假设不考虑该部分费用；③年引、供水费用 ，包括煤矿疏干水引水至蓄水池费用I31和蓄水池供水至用水目标费用I32；④年蒸发损失费用I4；⑤年渗漏损失费用I5；⑥年运行管理费I6；⑦年大修理费I7。

1.3 目标函数

根据蓄水池的建设费用组成，在蓄水池容积V及年供水量Q供确定的条件下，目标函数为单位体积供水的成本最低。则目标函数为：

(1)

1.4 池底边长L或池底半径R

由于深挖式蓄水池蓄水部分均为地面以下开挖部分，若计算各部分费用，首先需要确定池底边长L或池底半径R，根据蓄水池容积V及挖深H，可得方形蓄水池池底边长L计算公式如下：

(2)

同理圆形蓄水池底边半径R计算公式如下：

(3)

式中：L、R分别为蓄水池底边长和半径，m；H为蓄水池挖深，m；m1为蓄水池池内坡比；V为蓄水池容积，万m3；ΔL为马道宽度，m。

1.5 蓄水池各部分费用计算

1.5.1建筑费用

(1)土坝填筑费用I11。根据工程特性，蓄水池蓄水部分位于地面以下，因此土坝填筑部分仅为地面上部超高部分填筑，断面见图1。由于水池开挖土方可以直接用于土坝填筑，且运距很短，土坝填筑费用不考虑运距，只考虑碾压夯实等单价费率，具体计算公式如下：

(4)

(注：若设马道，则在第二项括号里加马道宽度2ΔL。)

式中：i11为坝体土料碾压、夯实等项的单价费率(定额)之和，元/m3；Ad为地面上土坝断面面积，其余各参数见图1所示。

图1 蓄水池土坝剖面图Fig.1 Sectional view of the reservoir dam

(2)护坡费用I12。

I12=I底+I内坡+I外坡=

i12底S底+i12内坡S内坡+i12外坡S外坡

(5)

式中：i12底、i12内坡和i12外坡分别为池底、池内侧和池外侧坡护砌单价，元/m2；S底、S内坡和S外坡为蓄水池到底面积、内侧坡面积及外侧坡面积，均根据L(R)、H及相关参数求得。

(3)防渗费用I13。

I13=I底+I内坡=i13底S底+i13坡S内坡

式中：i13底、i13坡分别为蓄水池池底防渗和池内侧边坡防渗单价，元/m2。

(4)蓄水池土方开挖费用I14。

I14=i14V

(7)

式中：i14为蓄水池开挖、运输等项的单价费率(定额)之和，各费率为根据施工组织综合考虑不同土类、运距及开挖方法后的综合费率，元/m3。

1.5.2固定资产的折旧费I′1

根据《水利工程管理单位供水部分固定资产基本折旧率和大修理费率表》，取折旧费率为2%。

I′1=I1×2%

(8)

1.5.3年引、供水费用I3

(1)年引水费用I31。露天煤矿疏干水引至蓄水池所消耗的电能的电费为：

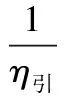
(9)

(2)年供水费用I32。蓄水池供水所消耗的电能的电费为：

(10)

式中：Q引为露天煤矿疏干水引入蓄水池水量，万m3；Q供为蓄水供水水量，万m3，其中Q供=Q引-Q蒸-Q渗-Q损；Q蒸为蓄水池年蒸发水量，万m3；Q渗为蓄水池年渗漏水量，万m3；Q损为蓄水池年其他损失水量，万m3；H引为露天煤矿疏干水引至蓄水池的水泵净扬程，m；H供为蓄水池至供水目标水泵净扬程及损失，m；η引、η供为引、供水的装置效率；i3为用电单价，元/kWh。

1.5.4年蒸发损失费I4

水面蒸发可根据水库附近蒸发站或气象站蒸发资料折算成自然水面蒸发，则蓄水池蒸发损失计算公式为：

(11)

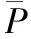
1.5.5年渗漏损失费用I5

渗漏损失大小与地质情况、防渗形式、水位高低等多种因素有关，无法较为准确的计算，本文渗漏损失参考平原水库渗漏统计资料，按库容的1%进行估算[2]。即：

I5=i5V×1%

(12)

式中：i5为露天煤矿疏干水供给蓄水池的引水成本，元/m3；V为蓄水池的总容积，万m3。

1.5.6年运行管理费费I6

I6=I1ξ

(13)

式中：ξ为年运行管理费率，取值3%～5%[3]，取4%；

1.5.7年大修理费I7

I7=I1×0.75%

(14)

1.6 蓄水池挖深优化模型求解

根据已建的数学模型，可知蓄水池挖深H的优化设计模型是一个非线性规划问题，目前关于非线性规划求解算法较多，各种算法都有特定的适用范围。MATLAB软件作为MathWorks公司出品的商业数学软件，是一个包含大量计算算法的集合。其有600多个工程中要用到的数学运算函数，可以方便的实现用户所需的各种计算功能。其具有以下3方面的优势：①具有高效的数值计算及符号计算功能，②具有完备的图形处理功能，③具有友好的用户界面及接近数学表达式的自然化语言。因此本研究蓄水池挖深优化模型采用MATLAB中关于非线性优化函数进行求解。并利用MATLAB编程语言编制了优化计算程序，可以实现直观、方便的参数输入。

MATLAB中非线性规划的数学模型写成以下形式：

式中：f(H)是标量函数，A，B，Aeq，Beq是相应维数的矩阵和向量C(H)；Ceq(H)是非线性向量函数。

模型求解则通过调用MATLAB内置非线性规划函数求得最优挖深H，同时利用MATLAB的图像显示功能，将目标函数在取值范围内曲线绘出，可直观了解挖深H与供水单价之间的关系。

2 模型应用

2.1 工程概况

根据《内蒙古准哈诺尔露天煤矿可行性研究报告》，以下简称《可研报告》，准哈诺尔露天煤矿可采毛煤量1 436.93 Mt，设计年原煤年产量为12.00 Mt，设计服务年限为104.13 a。根据《可研报告》蓄水池供水近期目标为煤化工园区，年供水量为1 500 万m3，远期供水目标为乌里雅斯太工业园区，年供水量60.4万m3。

工程根据煤矿设计疏干水量和用水量，确定疏干水蓄水池总容积650万m3，蓄水池地面以上四周为均质土坝，坝高2 m，坝顶宽10 m，当蓄水池挖深大于10 m时设马道，马道宽为5 m，蓄水池内侧边坡取1∶3，外侧边坡取1∶2.5。疏干水至蓄水池引水管道采用DN1000焊接钢管，蓄水池供水泵站位于蓄水池土堤外侧，泵站加压后通过一条长5.14 km的DN700钢管将水直接输送到煤化工园区水厂。

2.2 模型参数说明及输入

根据工程实际情况，编制挖深优化计算程序，界面见图2，具体各参数、参数值及说明见表1。

2.3 模型求解

根据蓄水池建筑结构尺寸和挖深优化计算模型，输入相应参数并优化计算，可得内蒙古准哈诺尔露天煤矿蓄水池最优池挖深为14.36 m，最优池底边长为624.05 m，最小供水单价为1.053元/m3。具体见图3优化计算成果图。

2.4 小 结

根据计算结果，可得蓄水池设计容积为650.00万m3，当蓄水池挖深为14.36 m时，蓄水池平均每年的单位供水成本最低。虽然模型建立过程中部分参数进行了简化，但对于挖深H的确定基本可以满足工程设计要求。根据优化结果，准哈诺尔煤矿深挖式蓄水池实际挖深H取为14.50 m。

图2 参数输入及参数值图Fig.2 The paramete input and parameter values chart

表1 参数说明Tab.1 Parameter description

图3 优化计算成果图Fig.3 The optimization calculation results chart

3 结 语

(1)本文在分析研究了深挖式蓄水池挖深H对工程建设及运行成本影响基础上，建立了挖深式蓄水池优化设计的非线性规划数学模型。并利用MATLAB编程语言编制了优化计算程序。

(2)根据所建立的优化设计模型，以内蒙古准哈诺尔煤矿蓄水池设计为实例，进行了实证计算分析。分析结果表明，蓄水池设计容积650.00万m3，当蓄水池挖深为14.36 m时，蓄水池平均单位供水成本最低。

(3)模型虽然基于若干假定条件，但其仍具有相当的适用性，能为一大批露天煤矿建设蓄水池的优化设计提供参考，有利于水资源的高效利用和节约投资。

□

[1] 周 建.平原水库优化设计研究[D]. 山东泰安：山东农业大学,2007.

[2] 卢 华,刘福胜,王少杰,等.基于遗传算法的平原水库优化[J].人民黄河,2011,33(1).

[3] 李三省.水库工程年运行管理费费率统计与分析[J].水利经济,1994,(4):63-64.

[4] 解可新.最优化方法[M].天津:天津大学出版社,1997.

[5] 屠晓峰.供水成本与理论价格计算方法初探[J].水利经济,1999,(1):33-36.

[6] 赵书兰.MATLAB编程与最优化设计应用[M].北京:电子工业出版社,2013.