原子费米气体附近BCS-BEC过渡区Ginzburg-Landau方程组稳态解的存在性

蓝丽红，金玲玉*

（华南农业大学数学系，广东广州510642）



原子费米气体附近BCS-BEC过渡区Ginzburg-Landau方程组稳态解的存在性

蓝丽红，金玲玉*

（华南农业大学数学系，广东广州510642）

摘要：研究了费米-玻色模型中Feshbach共振附近费米原子气体超流中所呈现的依赖于时间的Ginzburg- Landau （TDGL）方程组，并得到了该方程组在一定条件下稳态解的存在性及正则性。

关键词：稳态解；Ginzburg- Landau方程；山路引理

BCS- BEC过渡现象最早被发现于1992年［1-2］，众多学者对原子费米气体超流中所呈现的BCS- BEC过渡现象进行了研究［3-6］。另外，Ginzburg- Landau理论在原子费米气体超流的研究史上扮演了重要的角色，这是由于它能够捕获超流体在宏观上［7-8］所能呈现出来的几乎所有特征。在文献［6］中，M. Machida等建立了在费米-玻色模型中Feshbach共振附近费米原子气体超流中所呈现的依赖于时间的Ginzburg- Landau方程模型如下

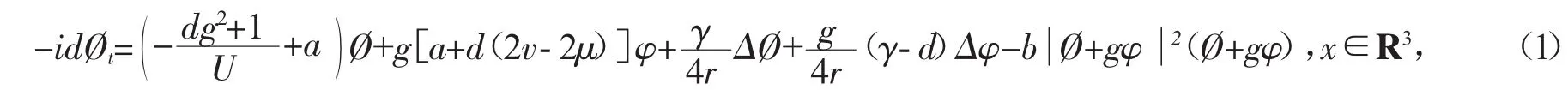
首先给出一些符号和预备知识。令Hr1（RN），LrP（RN）为径向对称函数的Sobolev空间。记C和c为任意的正常数。将方程（2）两边同乘以- dg，并加上方程（1）得

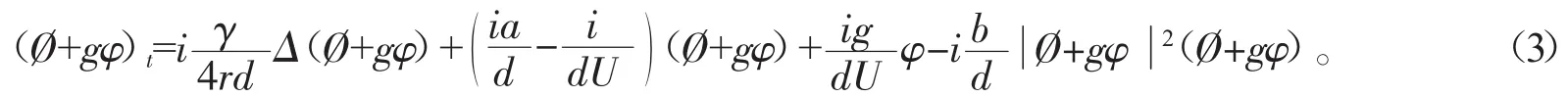
记W=覫+gφ，则方程组（2）、（3）等价于

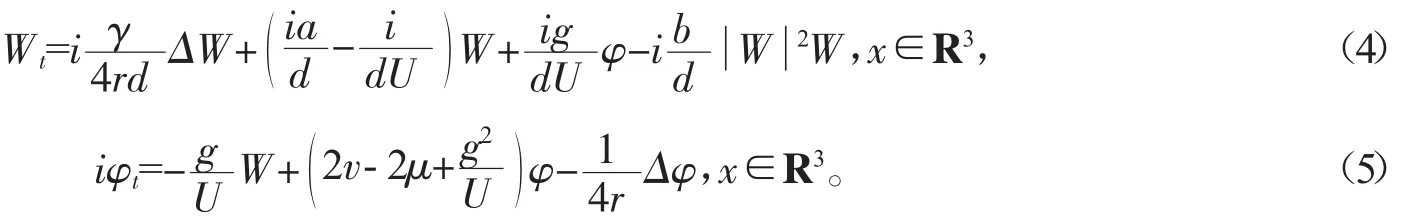
对方程（4）、（5），考虑其稳态解（驻波解）。令

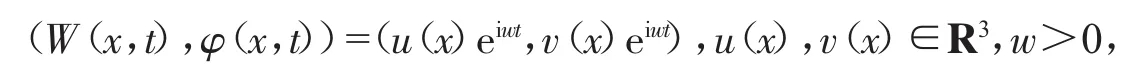
则u，v满足

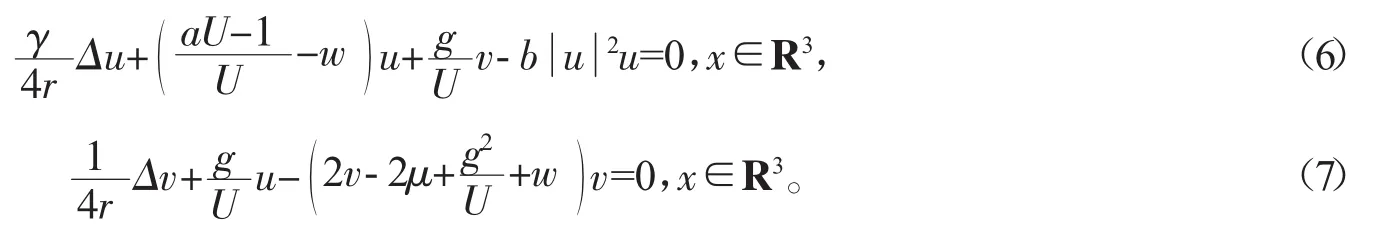
记

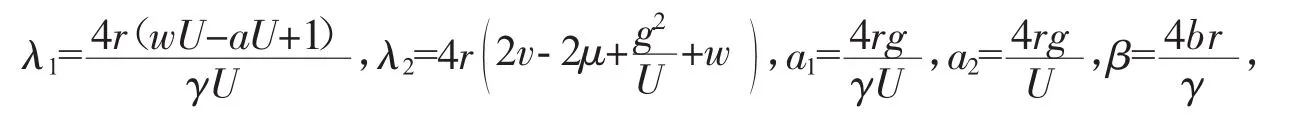
则方程（6）、（7）可简化为

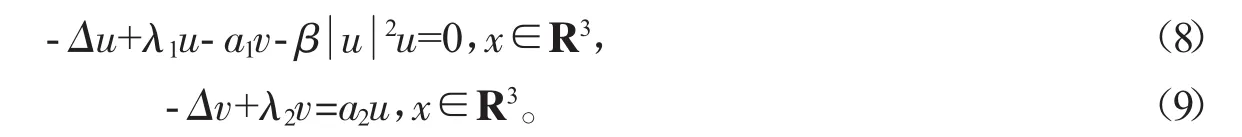
对任意λ2＞0，u∈Hr1（R3），方程（9）的解可表示为

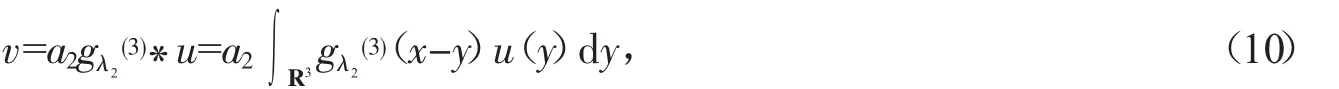
其中gλ2

(3)为算子-△+λ2的基本解。方程组（8）、（9）的弱解

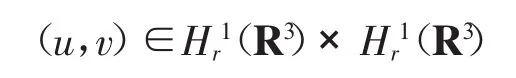
可转化为

的弱解，其中α=a1a2。

主要结果如下：

定理1假定λ1＞0，λ2＞0，β＞0，存在一个常数λ*＞0，使得α∈（-∞，λ*），则问题（11）有一个解，即问题（1）、（2）有稳态解。

定理2令u∈H1（RN）是方程（11）的解，则u∈C2，v（RN），其中0＜v＜1。

1方程组（1）、（2）稳态解的存在性

定义函数Iα：Hr1（R3）→R

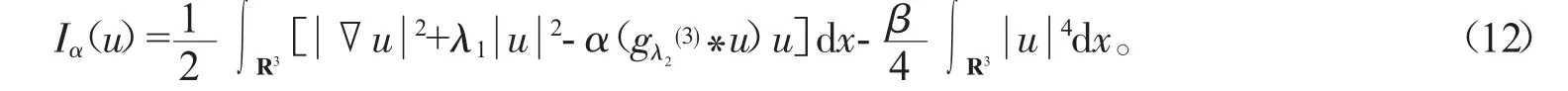
由于Iα函数在临界点的值就是方程（11）的弱解。下面先给出函数Iα的一些性质。由方程（9），对任意λ2＞0有

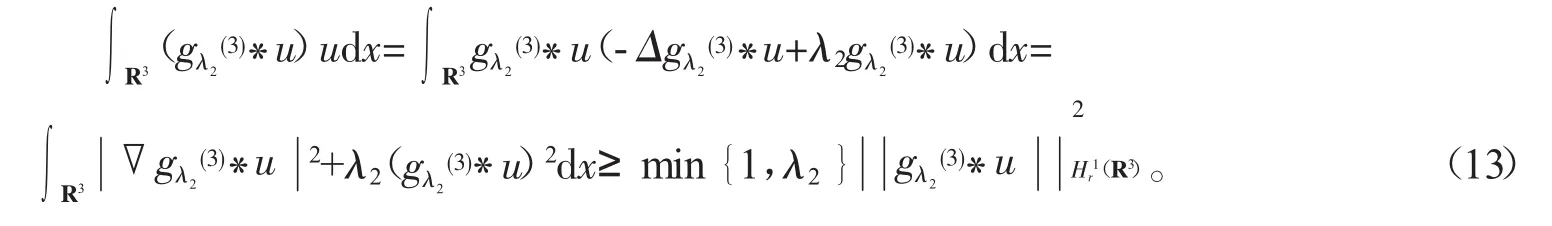
利用Holder不等式可知

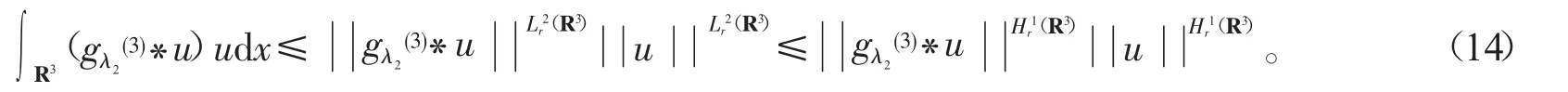
由式（13）、（14）可得

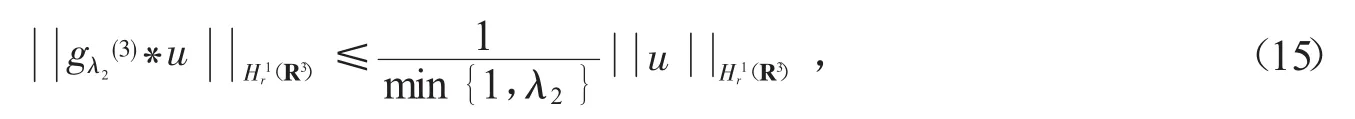
其中C为正常数。

引理1假定β＞0，λ1＞0，λ2＞0，函数Iα满足山路引理［15］条件：

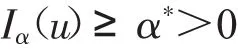
证明考虑α＜0的情形，有

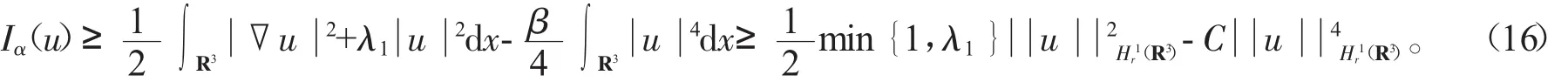
对α＞0的情形，利用式（15）及Sobolev不等式可得

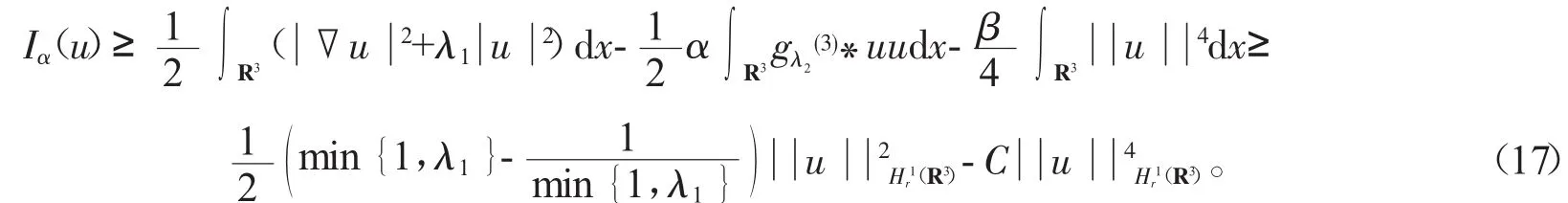
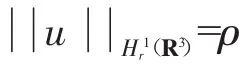
，利用式（16）和（17），存在一个常数α*＞0，使得Iα≥α*＞0。

固定一个u∈Hr1（R3），则

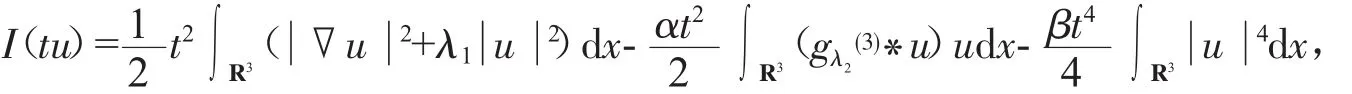
令t→+∞，则有Iα（tu）→-∞。故引理1得证。

定义

显示，M≥α*。利用引理1及山路引理［15］可知，存在一个（PS）序列unλ λ奂Hr1（R3），使得当n→∞时，有

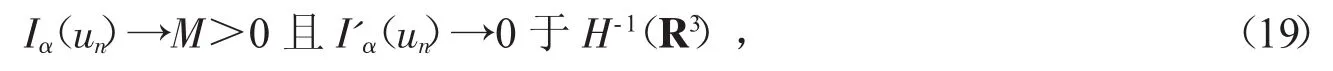
其中H-1（R3）记为Hr1（R3）的对偶空间。

引理2在引理1的条件下，由式（19）可得（PS）数列unλ λ在H1（RN）上有界。

证明由式（18）、（19）有

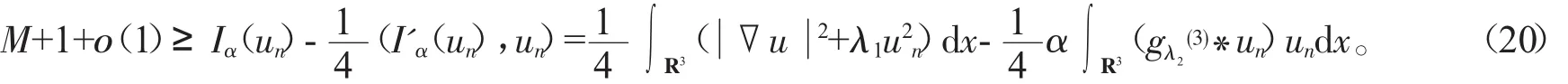
当α＜0时，有

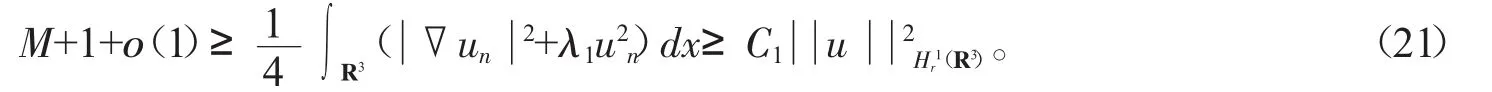
考虑α＞0的情形，由式（15）和式（20）有

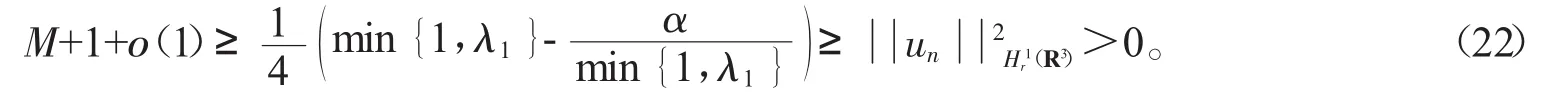
其中C1是正常数，选取α＜minλ 1，λ2λminλ 1，λ1λ，则式（22）中最后一个不等式成立。

利用式（21）、（22），对所有α＜λ*，存在一个常数λ*＞0，使得数列λunλ在Hr（1R3）上有界。故引理2证明完毕。

引理3泛函I（αun）的（PS）序列（满足式（19））具有收敛子列。

证明由引理2知序列λunλ在Hr（1R3）上有界，则存在u∈Hr（1R3），当n→∞时，存在子列（不妨记为un）：un→u弱收敛于Hr（1R3），un→u强收敛于Lr（pR3），1＜p＜6。

下面证明un→u且u≠0。由式（19）得

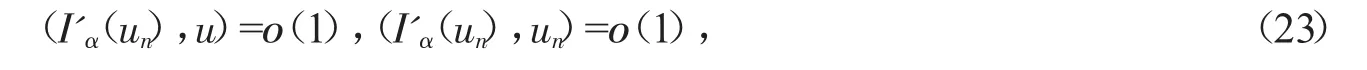
i.e.

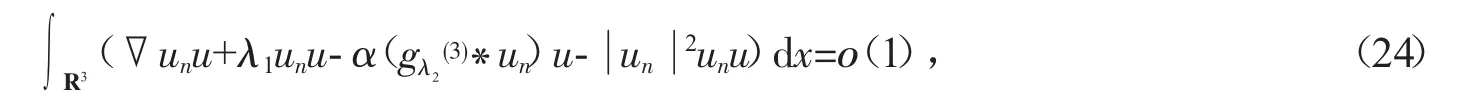
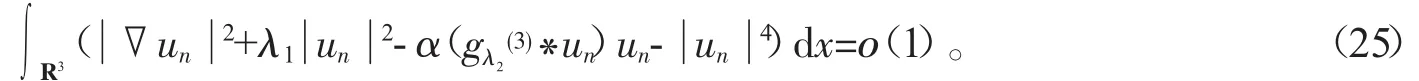
由于当n→∞时，有

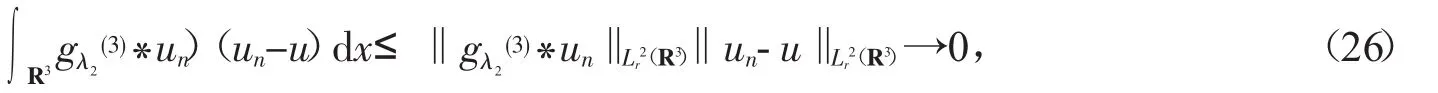
及

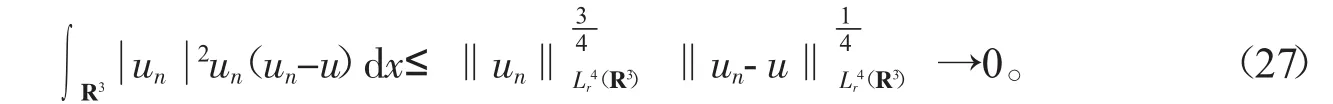
2正则性

本节将讨论方程（11）解的正则性，首先回顾一些基本的结果。引理4［16］Helmholtz方程在RN中的基本解是

的一个解，其中μ∈C和gμ（N）满足：

（1）当x≠0时，gμ（N）＞0且gμ（N）∈C∞（RN｛｝）；

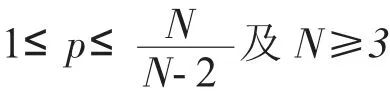
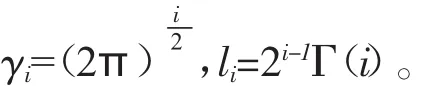
定理2的证明假定u∈Hr（1R3）是方程（11）的解。由引理4知，对1≤p＜3有g(λ32)∈L（pR3）。利用卷积的Young不等式可得

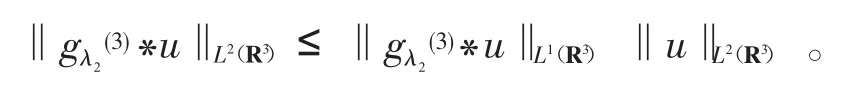
则gλ2(3)* u∈L（2R3）。显然由Sobolev嵌入不等式知‖u‖2u∈L（2R3）。利用方程（11）得u∈W2，（2R3），从而当0＜v＜1时有u∈C0，（vR3）。应用靴带技巧可推知，当0＜v＜1时有u∈C2，（vR3）。故定理2证明完毕。

参考文献：

［1］DRECHSLER M, ZWERGER W. Crossover from BCS- superconductivity to Bose- condensation［J］. Ann Phys, 1992, 504（1）: 15- 23.

［2］MELO C A, RANDERIA M, ENGELBRECHT J R. Crossover from BCS to Bose superconductivity: Transition temperature and time- dependent Ginzburg- Landau theory［J］. Phys Rev Lett, 1993, 71: 3202- 3205.

［3］HOLLAND M. Resonance Superfluidity in a Quantum Degenerate Fermi Gas［J］. Phys Rev Lett, 2001, 87（12）: 120406-120409.

［4］OHASHI Y, GRIFFIN A. The BCS- BEC Crossover in a Gas of Fermi Atoms with Feshbach Resonance［J］. Phys Rev Lett, 2002, 89（13）: 130402- 130406.

［5］TIMMERMANSE. Prospect ofcreatinga composite Fermi- Bose superfluid［J］. Phys Lett A, 2001, 285: 228- 233.

［6］MACHIDA M, KOYAMA T. Time- dependent Ginzburg- Landau theory for atomic Fermi gases near the BCS- BEC crossover ［J］. Phys Rev A, 2006, 74: 033603- 033608.

［7］GENNESP G. Superconductivityof Metals and Alloys［M］. Boulder, CO: WestviewPress, 1988.

［8］ABRIKOSOVAA. Fundamentals ofthe Theoryof Metals［M］. NewYork : Elsevier- Science Ltd, 1988.

［9］CHENSH, GUOBL. On the Cauchy Problemofthe Ginzburg- Laudau Equations for Atomic Fermin Gases Near the BCS- BEC Crossover［J］. J Partial Differential Equations, 2009, 22（3）: 218- 233.

［10］FANG S M, JIN L Y, GUO B L. Global attractor for the initial- boundary value problems for Ginzburg- Landau equations for atomic Fermi gases near the BCS- BECcrossover［J］. Nonlinear Anal Theor, 2010, 72（11）: 4063- 4070.

［11］KIKUCHI H, OHTA M. Stabilityofstandingwaves for the Klein- Gordon- Schrodinger system［J］. J Math Anal Appl, 2010, 1 （365）: 109- 114.

［12］ZHANG W G, QIN Y H, ZHAO Y, et al. Orbital stability of solitary waves for Kundu equation［J］. J Differential Equations, 2009, 247（5）: 1591- 1615.

［13］GUI C. Existence of mmulti- bump solutions for nonlinear schrodinger equations via variational method［J］. Comm Partial Differential Equations, 1996, 21: 787- 820.

［14］WANGZP, ZHOUH S. Positive solution for a nonlinear stationaryschrodinger- possion system in R3［J］. Discrete Contin Dyn Syst, 2007, 18（4）: 800- 818.

［15］AMBROSETTI A, RABINOWITZ P H. Dual vartional methods in critical point theory and applications［J］. J Funct Anal, 1973, 14: 349- 381.

［16］STUART C A. An introduction to elliptic equations on RNNonlinear Functional Analysis and Applications to Differential Equations［M］. Singapore: World Scientific, 1998.

【责任编辑：王桂珍foshanwgzh@163.com】

Stationary solutions for a Ginzburg- Landau system with atomic Fermi- gases near the BCS- BEC crossover

LANLi- hong, JINLing- yu
（Department of Mathematics, South China Agricultural University, Guangzhou 510642，China）

Abstract:In this paper, we investigate the time- dependent Ginzburg- Landau (TDGL) equations come from the superfluid atomic Fermi- gases near the Feshbach resonance from the fermion- boson model. We prove the existence of the stationary solution for this system under some conditions. And the exponential decay of the solution is obtained in our paper.

Keywords:stationarysolution; Ginzburg- Landau system; mountain- pass theorem

文章编号：1008- 0171（2016）01- 0035- 05

*通信作者：金玲玉（1979-），女，湖北荆州人，华南农业大学副教授。

作者简介：蓝丽红（1990-），女，畲族，广东河源人，华南农业大学硕士研究生。

基金项目：国家自然科学基金资助项目（11101160，11271141）

收稿日期：2015-05-28

中图分类号：O241.8

文献标志码：A