仓内稻谷干燥的多尺度多层结构热质传递模拟及试验

李　艳，徐英英，袁月定，赵　哲，袁越锦（. 陕西科技大学电气与信息工程学院，西安 700； . 宜春学院数学与计算机科学学院，宜春 336000）



仓内稻谷干燥的多尺度多层结构热质传递模拟及试验

李艳1，徐英英1，袁月定2，赵哲1，袁越锦1
（1. 陕西科技大学电气与信息工程学院，西安 710021； 2. 宜春学院数学与计算机科学学院，宜春 336000）

摘要：为研究仓内稻谷干燥的热质传递机理，确定稻谷颗粒内部不同组织结构特性对干燥过程的影响，以仓内稻谷堆为研究对象，针对谷粒的多层结构问题，运用多尺度理论、热质传递原理和孔道网络方法等知识，建立了仓内稻谷热风干燥的多尺度多层结构热质传递模型，并进行了稻谷堆热风干燥试验，模拟分析了仓内稻谷的干基含水率、温度分布以及孔隙汽相的温度分布等情况。结果表明：建立的热质传递模型可有效模拟仓内稻谷干燥过程，干燥器尺度下仓内稻谷的平均干基含水率的模拟值与试验值的最大相对误差为7.6%，颗粒尺度下单颗粒稻谷干基含水率的模拟值与试验值的最大相对误差约为6.8%；稻谷颗粒内部传热比传质速率快，颗粒内存在较大的水分梯度。稻谷胚扩散系数对干燥的影响较大，其次是稻谷壳扩散系数，稻谷衣扩散系数影响最小。研究结果为稻谷就仓干燥的品质及工艺分析提供了理论基础。关键词：干燥；模型；谷物；稻谷；多层结构；多尺度

李艳，徐英英，袁月定，赵哲，袁越锦. 仓内稻谷干燥的多尺度多层结构热质传递模拟及试验[J]. 农业工程学报，2016，32（2）：258－265.doi：10.11975/j.issn.1002-6819.2016.02.037http://www.tcsae.org

Li Yan， Xu Yingying， Yuan Yueding， Zhao Zhe， Yuan Yuejin. Multi-scale and multi-layer structural heat and mass transfer modeling and experiment on drying of rice in bin[J]. Transactions of the Chinese Society of Agricultural Engineering （Transactions of the CSAE）， 2016， 32（2）: 258－265. （in Chinese with English abstract）doi：10.11975/j.issn.1002-6819.2016.02.037 http://www.tcsae.org

0　引　言

目前，对农产品颗粒物料干燥过程的机理及模拟研究，传统的方法主要是连续介质法，即将这类物料视为虚拟的连续湿固体，不考虑物料堆中颗粒骨架与孔隙的差别，也不考虑颗粒内部组织结构的不同，直接运用现有热质传递等理论进行建模求解[1-5]。而事实上，农产品颗粒物料干燥时随机堆积，结构复杂，在大部分情况下更接近于离散介质[6-7]；且其骨架颗粒内部是一个多层物理结构，包括种皮（壳）、种衣和胚体等组织。显然，忽略这些因素对干燥过程的影响是不符合实际情况的。

多尺度理论是研究各种不同空间尺度或时间尺度相互耦合现象的科学。经过近30 a的发展，多尺度理论已是流体动力学[8]、材料科学[9]、环境科学、化学、气象学和高能物理等[10-12]科学的核心理论之一。孔道网络干燥理论是在20世纪90年代初，Daian和Saliba以及Nowicki 等[13]率先将渗流理论中常用的孔道网络方法引入到多孔介质干燥理论中，后经Prat和Yiotis等[14-21]进一步研究完善而逐渐发展起来的。这一理论认为多孔介质的湿分迁移在孔隙中具有很大优势，用一系列规则排列的节点及与其相互连接的孔道来重现多孔介质孔隙空间的几何及拓扑结构，直接在孔道等级上研究干燥过程中多孔介质的热质传递问题[22-27]。

本文拟将多尺度理论的基本思想引入稻谷颗粒物料干燥研究领域，综合运用热质传递原理、孔道网络方法等交叉学科的知识，建立其干燥过程的多尺度多层结构热质传递模型。并以稻谷堆为农产品颗粒物料的典型代表进行热风干燥试验验证，模拟分析仓内稻谷的干基含水率、温度分布以及孔隙汽相的温度分布等情况，以期为稻谷就仓干燥的品质及工艺分析提供理论基础。

1　试验材料与方法

选用稻谷（购于西安当地粮贸市场）为原料进行就仓热风干燥试验。首先，将稻谷除杂洗净并调质获得均匀一致的干基含水率（0.312 kg/kg）；然后，将稻谷置于干燥试验仓中进行热风干燥。同时测得稻谷堆主要结构特征参数如表1所示，其中孔隙率采用密度比较法测得；平均长轴粒径、短轴粒径和孔喉径采用统计计数法测得；孔隙个数面密度、颗粒个数面密度和孔隙配位数采用影像法测得。干燥试验仓是一个顶部无盖的立方体（图1），仓体内部尺度为200 mm（长）×100 mm（宽）×300 mm（高），仓内稻谷堆的高度为200 mm，仓材料为有机玻璃（厚8 mm）；仓底部中心处开一直角等腰三角形进风口，顶部与外界相通为热风出口；一正面（图1）上开了24个测量孔，并编号测量点11个。仓内稻谷的平均干基含水率和平均温度计算方法为：已测得干燥仓上的11个测量点的温度值Ti（i＝1，2，…，11），K；每个点对应的有效控制面积为Ai（i＝1，2，…，11），mm2。则该干燥仓内的稻谷平均温度（K）的计算公式为

同理，测得干燥仓上的11个测量点的干基含水率值Mi（i＝1，2，…，11），kg/kg。可得仓内稻谷平均干基含水率（kg/kg）的计算公式为

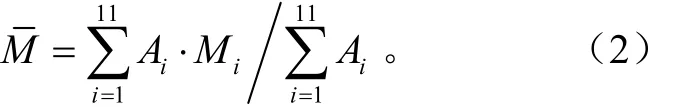
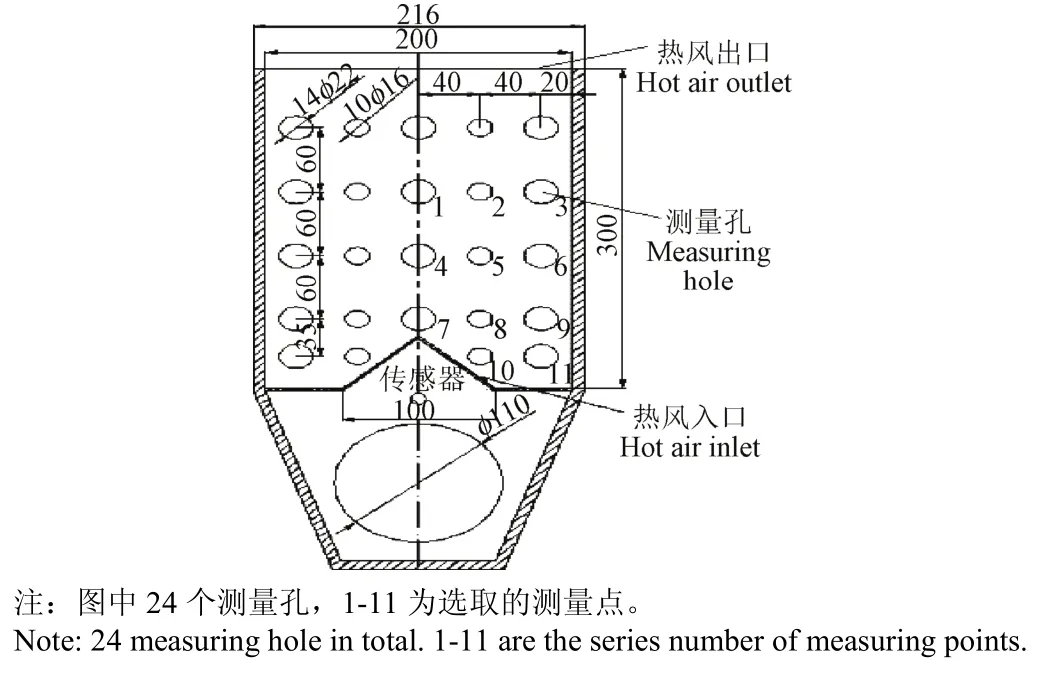
图1　干燥仓结构示意图Fig.1　Structure design map of drying container

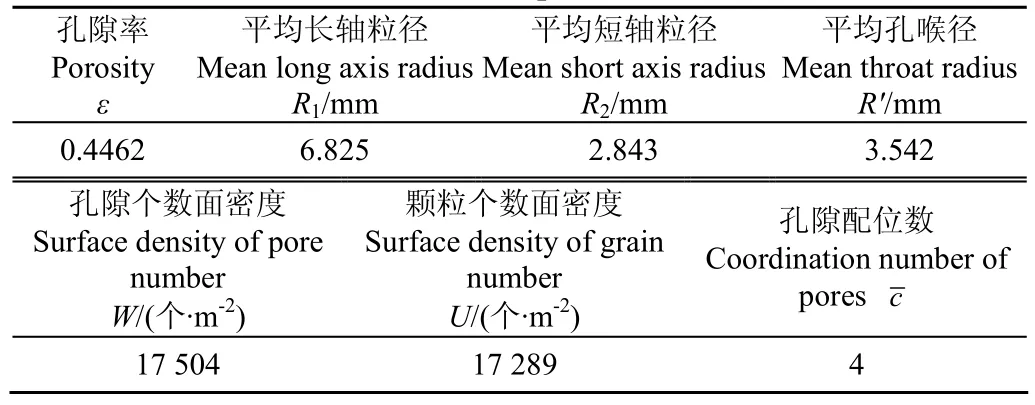
表1　稻谷堆主要结构特征参数值Table 1　Main structural parameters of rice stack

干燥试验开始时，仓进风口热风温度42.0℃，热风相对湿度6.5%，热风静压56.0 Pa；环境温度20.1℃；稻谷颗粒初始温度18.0℃，稻谷颗粒初始干基含水率0.312 kg/kg。干燥试验过程中，每隔一段时间拔开测量孔橡胶塞，采用美国Raytek公司的Raytek ST6型红外测温仪测量各点稻谷颗粒的温度；并从测量孔中取出适量稻谷样品，采用烘干法测得各样品的干基含水率。仓内稻谷堆中孔隙气相的温、湿度由埋入各测量点的温、湿度传感器测量。

2　二维多尺度多层结构传热传质模型

2.1物理模型

从上述试验过程可以看出，农产品颗粒物料就仓通风干燥主要是指热风在风压力的推动下，从物料的某个或多个方向进入其孔隙体系，与骨架颗粒进行热质交换后从另一个或多个方向排出的过程（图2a）[28]。显然，在该干燥过程中，孔隙是热质传递的优势通道。为区分颗粒骨架与孔隙的差别，本文采用文献[20]中的方法构建孔道网络物理模型如图2b所示。模型主要由“孔-喉-孔”网络和骨架两部分组成，孔为球体，喉为圆柱体，孔和喉径服从一定的概率分布。一个二维孔道网络物理模型可由分布律、两节点间距离、模型规模数、配位数等参数来描述[15，20]。其次，为考查骨架颗粒内部壳、衣、胚等组织结构不同对干燥过程的影响，本文将研究对象划分为颗粒尺度与干燥器尺度2个不同级别来处理。在颗粒尺度上，每一个骨架颗粒都具有种皮（壳）、种衣和胚体三层不同的物理组织结构，如图2c所示。

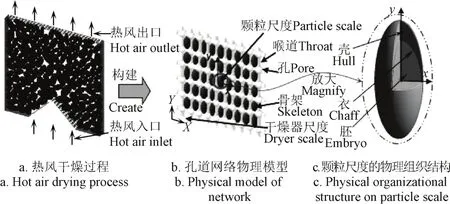
图2　多尺度多层结构模型Fig.2　Model of multi-scale and multi-layer

2.2数学模型

为简化数学模型，针对上述颗粒物料热风干燥过程，作如下基本假设：1）在颗粒尺度上假设骨架颗粒为具有多层物理结构的椭球体，不收缩、无变形；假设颗粒内部湿分传递主要依靠液态或汽态扩散；假设骨架颗粒内的水分相变所需耗热由骨架颗粒本身提供。2）在干燥器尺度上以对流换热为主，忽略热传导、辐射传热；对流传质为主，忽略扩散传质，不考虑有液相参与的各种传质；假设气相为不可压缩的理想气体。

2.2.1颗粒尺度

对于孔道网络物理模型中在颗粒尺度上的每个稻谷粒，考虑其对称性，只需取其整体的1/4对称面（图3）进行分析，运用雷可夫理论[6]描述其热质传递过程，由上述基本假设，经推导可得在圆柱坐标系下的热质传递控制方程组为式（3）：

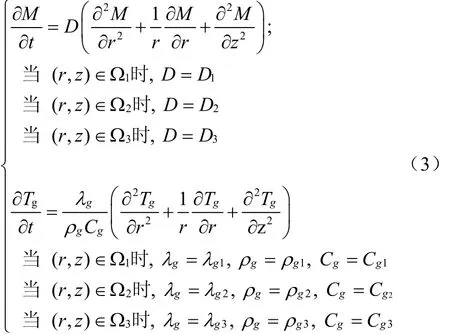
式中Tg为骨架颗粒内部某时刻某处的温度，K；λg为骨架颗粒热导率，W/（m·K）；ρg为骨架颗粒密度，kg/m3；Cg为骨架颗粒比热容，J/（kg·K）；M为骨架颗粒内部某时刻某处的干基含水率，kg/kg；D为颗粒内水分扩散系数，m2/s；t为时间变量，s；r、Z为圆柱坐标变量，m。

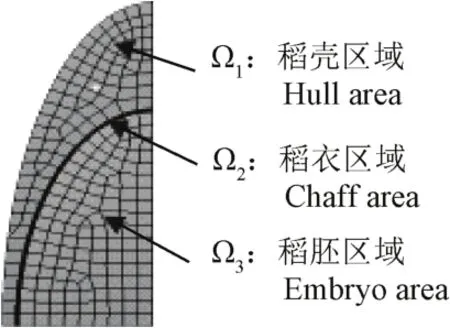
图3　稻谷粒内部结构与网格划分Fig.3　Inside structure and meshing generation of rice

方程组（3）的边界条件为：

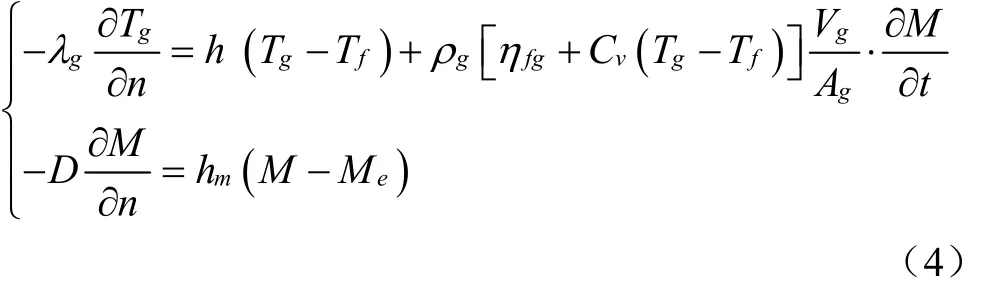
式中h为对流换热系数，W/（m2·K）；ηfg为汽化潜热系数，J/kg；Cv为水蒸气比热容，J/（kg·K）；Vg为颗粒体积，m3；Ag为颗粒表面积，m2；Tf为气流温度，K。hm为对流传质系数，m/s；Me为干基平衡含水率，kg/kg。

方程组（3）的初始条件为：

式中T0为谷粒初始时刻的温度，K；M0为谷粒初始时刻的干基含水率，kg/kg。

2.2.2干燥器尺度

如图2b，设在某一时刻nΔt，模型中某孔节点（i，j）内的水蒸汽密度为，则应用质量守恒、能量守恒与达西定律可推导获得在干燥器尺度上的传质、传热及动量传递控制方程组为

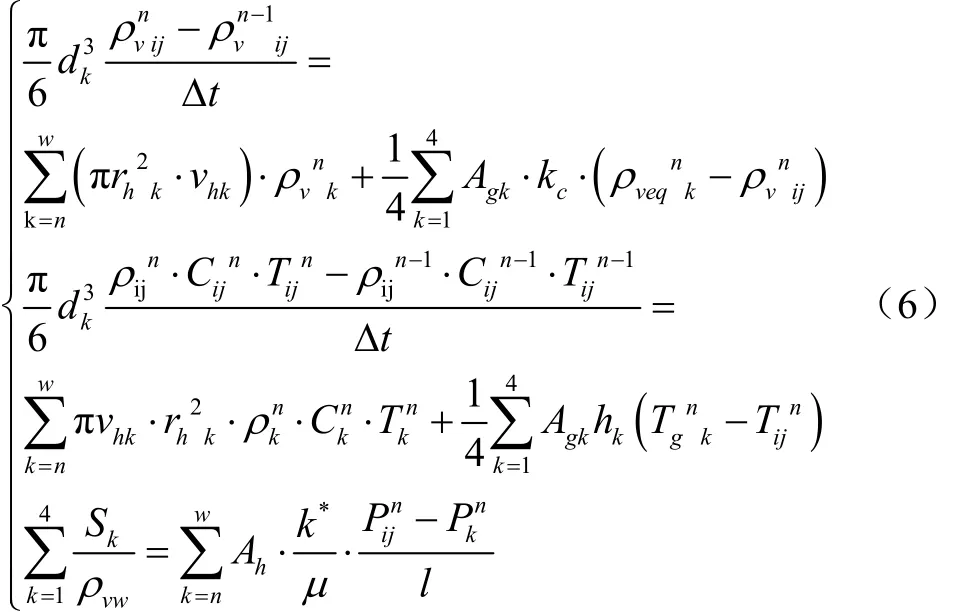
2.2.3跨尺度热质交换控制方程

上述2个尺度的方程之间没有联系，热质传递信息彼此分离，故需补充一定的跨尺度热质交换平衡方程方可使模型方程组封闭。

在孔道网络物理模型的每个骨架颗粒表面上，存在着跨尺度的热质交换，即该颗粒内水分的减少量等于气化流入颗粒周围孔隙的蒸汽量；同时，该颗粒内热焓变化量等于颗粒从周围气相中对流换热得到的热量减去气化颗粒内水分所耗的热量。于是应用质量守恒、能量守恒定律可得跨尺度的热质交换平衡方程组如式（7）

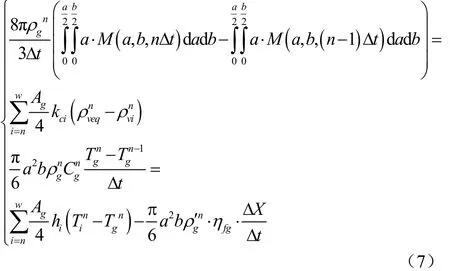
式中gρ′为颗粒的绝干密度，kg/m3；ηfg为水分气化潜热系数，J/kg；表示某一时刻颗粒密度，kg/m3；ɑ为颗粒短轴径，m；b为颗粒长轴径，m；Cg为颗粒比热容，J/（kg·K）；Ag为颗粒表面积，m2；kci为颗粒表面对流传质系数，m/s；n 表示时间序数；Tg为颗粒温度，K；ΔX为颗粒平均含水率差，kg/kg；hi为颗粒的对流换热系数，W/（m2·K）。

3计算机模拟

基于上述干燥模型，本文采用VC＋＋与MATLAB语言联合编程开发模拟程序。模拟程序主要由数学模型模块、物理模型模块及数据处理模块等组成；物理模型模块的主要功能是读取模型文件，根据节点、喉等坐标值生成物理模型框架，定义孔（节点）、喉、骨架等的结构属性；该模块采用VC＋＋编程，利用其面向对象的编程（OOP）技术，将物理模型中的各个组成部分如骨架颗粒、孔与喉等用OOP中的某个“类”的对象来表示，从而将各个组成部分的属性、相互关系等特性要素封装起来，使得数学模型模块在求解时能够较方便地访问各个组成部分，及时吸纳物理模型孔道结构信息。数学模型模块是本模拟程序的核心模块，主要完成数学模型的求解计算等，其计算量巨大，因此该模块主要采用MATLAB语言编程，以充分利用其强大的矩阵运算优势。求解过程中干燥器尺度控制方程和跨尺度热质交换平衡方程已是离散型的差分方程，直接采用有限差分的分离式解法求解；而颗粒尺度方程为偏微分形式，需先进行网格划分然后对其有限差分离散方可求解。稻谷颗粒为理想的椭球体，具有对称性，为提高计算速度，只需取其对称面的1/4进行分析，其网格划分如图3所示。计算机模拟流程图如图4所示。

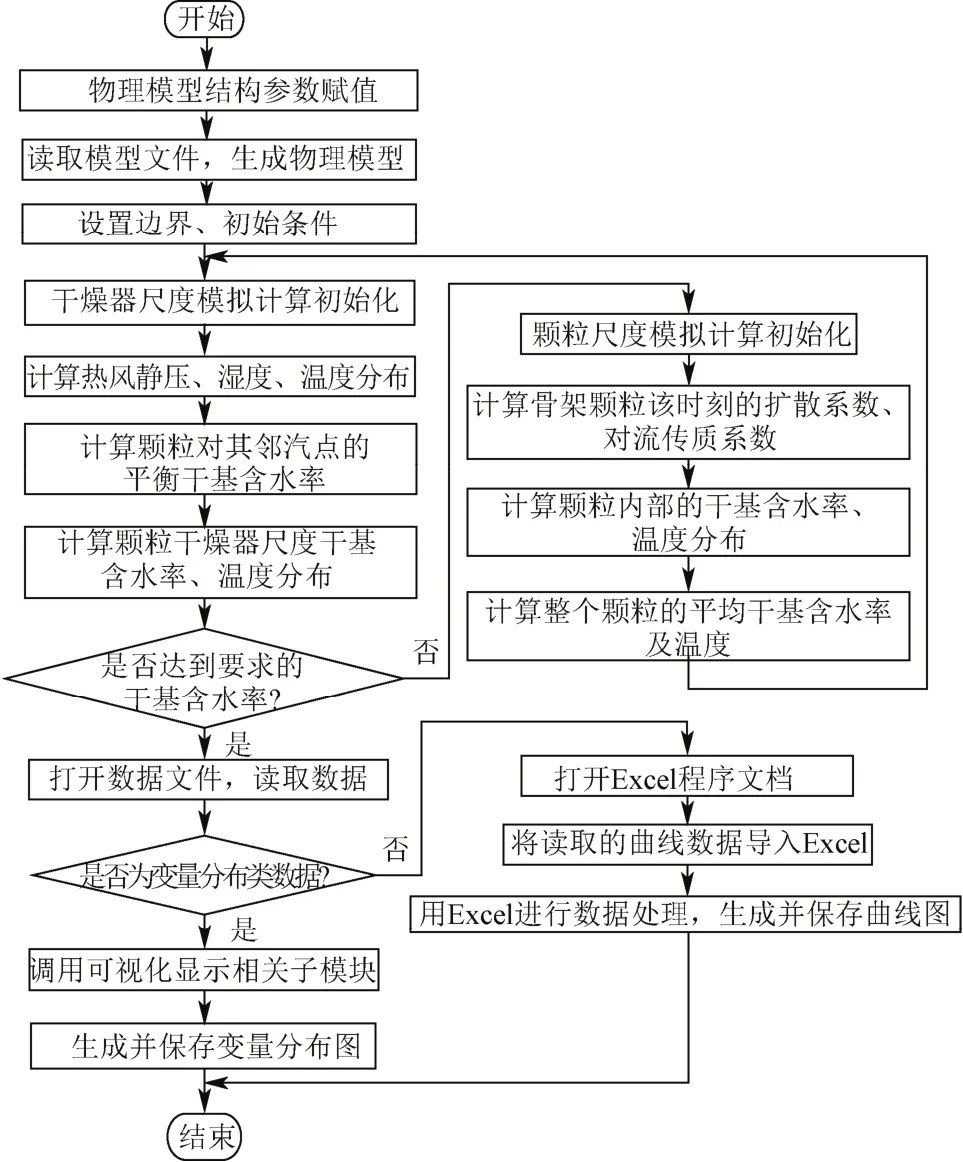
图4　计算机模拟流程图Fig.4　Flow chart of computer simulation

模拟计算过程中模型初始边界条件采用的工况参数与试验相同，即热风温度42.0℃，热风相对湿度6.5%，热风压力56.0 Pa；环境温度20.1℃；稻谷颗粒初始温度18.0℃，稻谷颗粒初始干基含水率0.312 kg/kg；对流换热系数h满足[29]

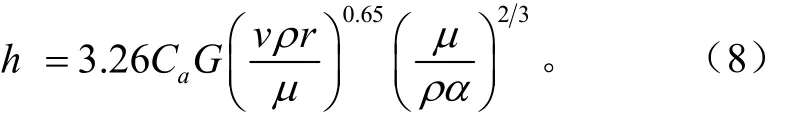
式中Cɑ为热风比热容，J/（kg·K）；G为热风质量流量，kg/（m2·s）；v为热风风速，m/s；r为颗粒半径，m；ρ为热风密度，kg/m3；μ为热风黏度，kg/（m·s）；α为颗粒导温系数，m2/s。

对流传质系数hm满足Frossling公式[29]，即

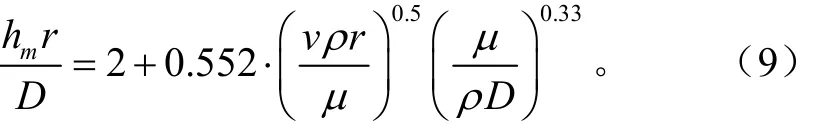
其他所需的主要模拟计算参数值如表2所示[29]。

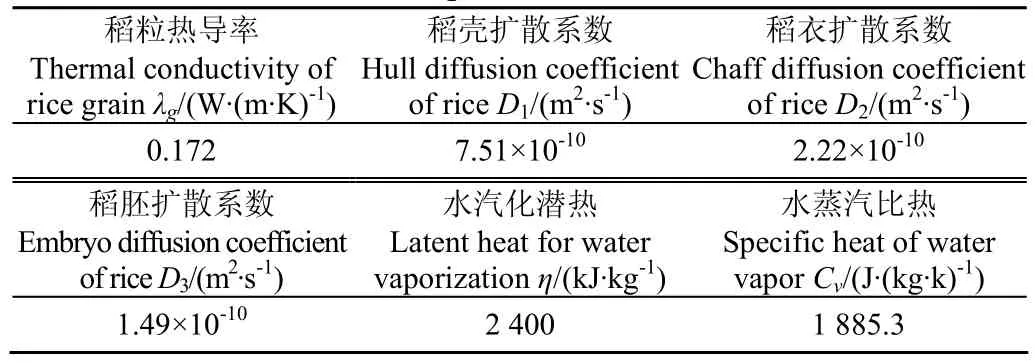
表2　模拟计算过程中采用的主要计算参数值Table 2　Main parameters for simulation

4　结果与分析

4.1干燥器尺度

4.1.1干燥仓内稻谷平均干基含水率变化曲线

图5为仓内稻谷颗粒的平均干基含水率曲线模拟与试验结果的比较。从图中可以看出，仓内稻谷颗粒的平均干基含水率随时间大致呈线性下降，模拟与试验变化曲线基本吻合，其最大相对误差约为7.6%。这从宏观上表明，本文在干燥器尺度上建立的模型合理有效。误差产生的原因主要有2个方面：一是试验与模拟情况不完全一致，如为了便于通过有机玻璃观察仓内稻谷的干燥情况，试验时没有对干燥仓进行完全绝热处理；二是试验数据的计算处理只采用了有限的11个数据为代表计算平均干基含水率，必然会产生计算误差，理论上只有测量点无数多时才能测得平均干基含水率的真值。

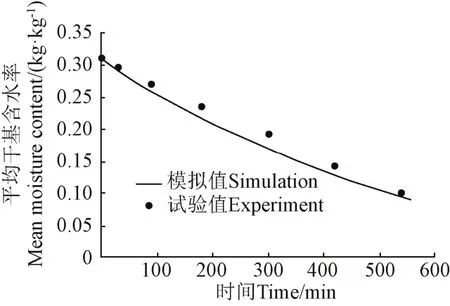
图5　仓内稻谷颗粒的平均干基含水率曲线模拟与试验结果的比较Fig.5　Average dry basis moisture content curves comparison of simulation and experiment

4.1.2仓内稻谷与孔隙内汽相平均温度变化曲线

从图6可以看出，仓内稻谷平均温度及孔隙汽相平均温度模拟与试验变化曲线趋势基本一致。在干燥初始阶段，稻谷与汽相温度均上升较快，随着时间的推移，温度曲线在平稳中有所上升。另外，从图中还可看出，稻谷温度无论是模拟还是试验值均比相应汽相温度低2 K左右，这说明传统干燥理论不区分颗粒骨架与孔隙的差别是不妥的。其原因主要在于干燥过程中，热风进入物料颗粒周围的孔隙中，其热量被骨架颗粒吸收，这时骨架颗粒开始升温，导致骨架颗粒中的水分因干燥汽化为水蒸气，水分汽化需要吸热，使得颗粒本身的温度又有降低趋势，所以颗粒骨架温度要比周围孔隙空气略低。

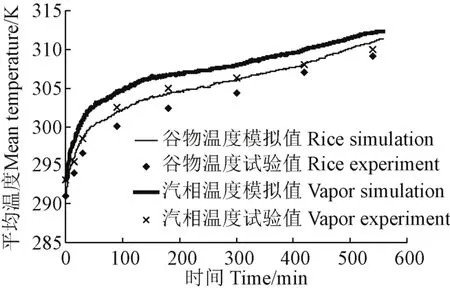
图6　稻谷颗粒和孔隙汽相平均温度曲线模拟与试验结果的比较Fig.6　Average temperature curves comparison of simulation and experiment

4.1.3仓内稻谷干基含水率、温度分布和孔隙汽相温度分布

如图7所示，依次为仓内稻谷颗粒的干基含水率分布、温度分布以及孔隙汽相的温度分布。从图中可以观测到干燥过程中仓内的各个分布随时间的变化情况。在干燥初始阶段，进风口处的稻谷温度和汽相温度均上升很快，接近热风温度，而在该处的干基含水率降低得要慢一些；其他区域的温度上升稍缓，尤其是上侧角部区域，温度和干基含水率几乎没有变化。随着干燥的进行，上侧角部区域逐渐缩小，中间区域整体上移。到了干燥末期，仓内大部分区域已接近热风温度，只有少量的稻谷尚未完全干燥。

图7　仓内中截面干基含水率和温度分布的模拟结果Fig.7　Dry basis moisture and temperature distributions of simulation for rice drying on middle section

4.2颗粒尺度

4.2.1单颗粒稻谷干燥曲线与干基含水率分布

从图8a可以看出，单颗粒稻谷干基含水率在干燥开始阶段下降较快，到干燥末期由于干燥速率下降曲线趋于平缓，稻谷干基含水率即将达到平衡干基含水率。总体上单颗粒稻谷干基含水率模拟与试验变化曲线吻合较好，其最大相对误差约为6.8%。这从介观上表明，本文在颗粒尺度上建立的模型合理有效。

图9a为模拟得到的稻谷颗粒内部的干基含水率分布。从图中可以看出，稻谷颗粒内中心部位干基含水率在干燥过程中一直较高，到干燥快结束时，中心部位水分干基含水率仍有约0.14 kg/kg，而在稻谷颗粒表层特别是谷尖处干基含水率已非常低，这势必造成颗粒内存在较大的水分梯度，而大水分梯度的存在将对稻谷干燥品质如应力裂纹等产生非常不利的影响。

4.2.2单颗粒稻谷温度曲线与温度分布

从图8b可以看出，进风口处单颗粒稻谷温度模拟与试验值变化曲线基本吻合。干燥过程中该处稻谷颗粒温度上升很快，几乎在干燥一开始的5 min内就已近似达到热风温度；这与在干燥器尺度温度场显示的结果一致。

图9b为模拟得到的稻谷颗粒内部的温度分布。从图中可以看出，干燥过程中颗粒内部温度分布随时间的变化很快，前3min温度直线上升，谷尖处最先近似达到热风温度，随后温度升高速度有所变慢，到5min时颗粒内部温度整体近似均匀一致。

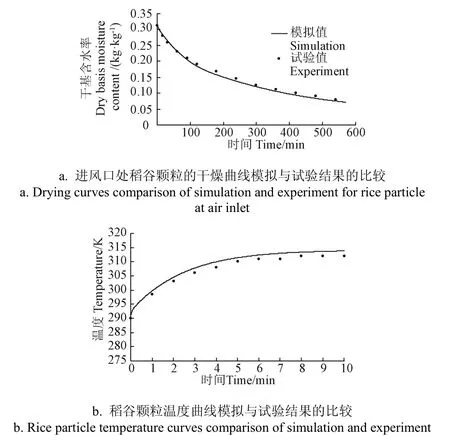
图8　试验结果与模拟结果的对比曲线Fig.8　Comparison curves between simulation and experiment

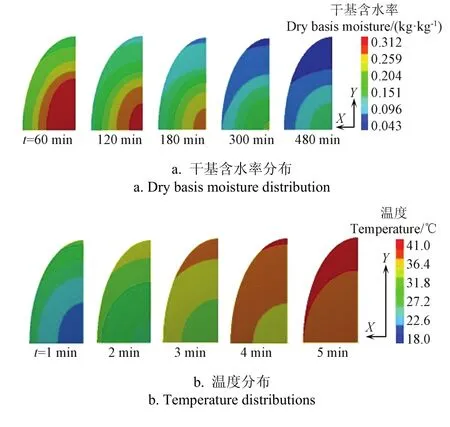
图9　稻谷颗粒内部干基含水率及温度分布Fig.9　Dry basis moisture contributions and temperature distributions of simulation for rice particle drying

4.2.3颗粒内部不同组织物理特性对干燥过程影响的模拟分析

稻谷壳、衣、胚扩散系数是影响稻谷干燥过程的重要因素。这些扩散系数是关于温度和含水率的函数[29]，是一变化值。为研究稻谷颗粒内部壳、衣、胚等不同组织结构特性对干燥过程的影响，本文将稻谷壳、衣、胚扩散系数分别设定为5种不同的值，进行相应干燥过程的模拟及分析。

1）不同壳扩散系数

将稻谷壳扩散系数设定为5种不同的值，其余参数如表2所示，进行颗粒物料干燥模拟，得到不同壳扩散系数下的颗粒干燥曲线如图10a所示。从图中可以看出，颗粒壳扩散系数对干燥过程有一定影响。随着壳扩散系数的减小，干燥速度逐渐变慢，达到相同干基含水率所需干燥时间越长。这主要是因为壳扩散系数越小，导致颗粒内湿分逸出壳表面越困难，干燥也就越慢。

2）不同衣扩散系数

将稻谷衣扩散系数设定为5种不同的值，其余参数如表2所示，进行颗粒物料干燥模拟，得到不同衣扩散系数下的颗粒干燥曲线如图10b所示。从图中可以看出，颗粒衣扩散系数对干燥过程的影响很小。随着衣扩散系数的减小，干燥速度虽有所变慢，但变慢的幅度特别小，可以忽略不计。这主要是因为颗粒种衣的组织物理厚度相对壳、胚来说薄得多，其扩散系数的变化对颗粒内部湿分迁移所起的作用有限。

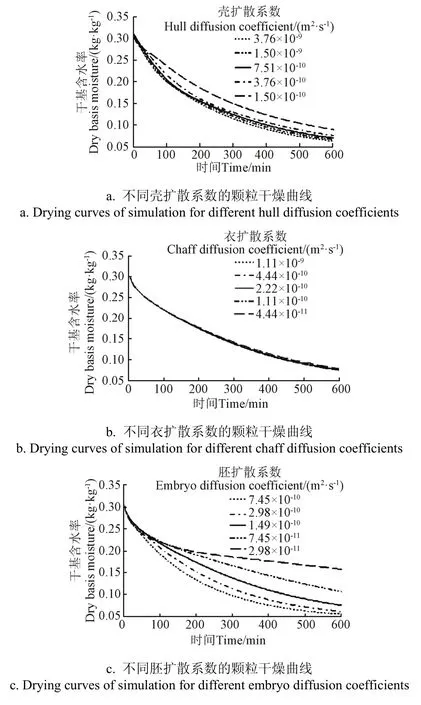
图10　不同扩散系数下的颗粒干燥曲线Fig.10　Drying curves of simulation for different diffusion coefficients

3）不同胚扩散系数

将稻谷胚扩散系数设定为5种不同的值，其余参数如表2所示，进行颗粒物料干燥模拟，得到不同胚扩散系数下的颗粒干燥曲线如图10c所示，干基含水率分布（t＝300 min时）如图11所示。

由图10c可以看出，颗粒胚扩散系数对干燥过程的影响较大。随着胚扩散系数的减小，干燥速度明显变慢，特别是干燥的中、后期，达到相同干基含水率所需干燥时间显著增加。这一方面是因为种胚在颗粒组织中占有较大比例；另一方面，从图11也可以看出，胚扩散系数越小，颗粒内湿分从胚内迁移到壳表面越困难，湿分仿佛被“囚禁”在胚内，如当胚扩散系数为2.98×10-11m2/s时，其颗粒中心区域的干基含水率几乎没有减小。因此，干燥也就越慢。

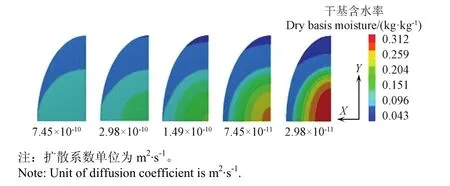
图11　不同胚扩散系数下的干基含水率模拟结果（t＝300min）Fig.11　Dry basis moisture distributions of simulation for different embryo diffusion coefficients（t＝300min）

5　结　论

本文建立的多尺度多层结构传热传质模型可有效模拟稻谷堆干燥过程。干燥器尺度下仓内稻谷颗粒的平均干基含水率的模拟值与试验值的最大相对误差为7.6%，颗粒尺度下单颗粒稻谷干基含水率的模拟值与试验值的最大相对误差约为6.8%。模拟得到的仓内稻谷平均干基含水率、温度变化曲线和单颗粒干燥曲线反映了其干燥过程的实际情况。在干燥过程中，特别是在非干燥终了阶段，稻谷温度比相应汽相温度低2 K左右，传统干燥理论不区分颗粒骨架与孔隙的差别是不妥的；稻谷颗粒内传热比传质速率快，进风口处颗粒内温度上升在5 min左右基本达到均匀一致，而颗粒内中心区域到干燥快结束时仍具有较高的干基含水率，颗粒内存在较大的水分梯度。

颗粒内部不同组织物理特性对稻谷干燥有较大的影响，稻谷胚扩散系数的影响较大，其次是稻谷壳扩散系数，稻谷衣扩散系数影响最小。在干燥过程中，随着胚扩散系数的减小，干燥速度明显变慢，特别是干燥的中、后期，达到相同干基含水率所需干燥时间显著增加。

[参考文献]

[1] 刘相东，杨彬彬. 多孔介质干燥理论的回顾与展望[J]. 中国农业大学学报，2005，10（4）：81－92. Liu Xiangdong， Yang Binbin. Review and vista on drying theories of porous medium[J]. Journal of China Agricultural University， 2005， 10（4）: 81－92. （in Chinese with English abstract）

[2] ElGamal Ramadan， Ronsse Frederik， Radwan Sherif M， et al. Coupling CFD and diffusion models for analyzing theconvective drying behavior of a single rice kernel[J]. Drying Technology， 2014， 32（3）: 311－320.

[3] Ranjbaran Mohsen， Emadi Bagher， Zare Dariush. CFD simulation of deep-bed paddy drying process and performance[J]. Drying Technology， 2014， 32（8）: 919－934.

[4] 胡志超，王海鸥，谢焕雄，等. 谷物横流干燥数学模型及模型预测控制[J]. 农业工程学报，2009，25（4）：96－102. Hu Zhichao， Wang Hai'ou， Xie Huanxiong， et al. Mathematical models and model predictive control for crossflow graindrying[J]. Transactions of the Chinese Society of Agricultural Engineering （Transactions of the CSAE），2009， 25（4）: 96－102. （in Chinese with English abstract）

[5] 颜建春，谢焕雄，胡志超，等. 固定床上下换向通风小麦干燥模拟与工艺优化[J]. 农业工程学报，2015，31（22）：292－300. Yan Jianchun， Xie Huanxiong， Hu Zhichao， et al. Simulation and process optimization of upward and downward reversing ventilating drying by fixed bed[J]. Transactions of the Chinese Society of Agricultural Engineering （Transactions of the CSAE）， 2015， 31（22）: 292－300. （in Chinese with English abstract）

[6] 王艳丽，塔娜，吴菲菲，等. 基于分形理论的谷物干燥试验研究[J]. 粮食与饲料工业，2014，12（4）：24－27. Wang Yanli， Ta Na， Wu Feifei， et al. Grain drying experiments based on fractal theory[J]. Cereal and Feed Industry， 2014， 12（4）: 24－27. （in Chinese with English abstract）

[7] 袁越锦，徐英英，刘相东. 仓内谷物通风干燥过程的孔道网络模型[J]. 农业机械学报，2009，40（8）：115－118. Yuan Yuejin， Xu Yingying， Liu Xiangdong. Pore network model for drying of corn material in bin[J].Transactions of the Chinese Society for Agricultural Machinery， 2009， 40（8）: 115－118. （in Chinese with English abstract）

[8] 杨晨，何航行. 气液两相分离的免方程多尺度模拟法[J].化工学报，2015，66（6）：2031－2040. Yang Chen， He Hangxing. Equation-free multi-scale simulation of two-phase gas-liquid separation[J]. CIESC Journal， 2015， 66（6）: 2031－2040. （in Chinese with English abstract）

[9] 吴可义，郭佳. 多尺度共轭微孔聚合物的可控合成[J]. 化学学报，2015，73（6）：480－486. Wu Keyi， Guo Jia. Controllable synthesis of multi-scale conjugated microporous polymer[J]. Acta Chimica Sinica，2015， 73（6）: 480－486. （in Chinese with English abstract）

[10] 岳安志，杨建宇，张超，等. 基于多尺度形态学滤波的高分辨率遥感影像分割[J]. 农业工程学报，2013，29（增刊1）：89－95. Yue Anzhi， Yang Jianyu， Zhang Chao， et al. Multi-scale morphological filter for image segmentation of very high resolution satellite imagery[J]. Transactions of the Chinese Society of Agricultural Engineering （Transactions of the CSAE）， 2013， 29（Supp.1）: 89－95. （in Chinese with English abstract）

[11] Perré P. Multi-scale modeling of drying as a powerful extension of the macroscopic approach: Application to solid wood and biomass processing[J]. Drying Technology， 2010，28（8）: 944－959.

[12] 张宝忠，许迪，刘钰，等. 多尺度蒸散发估测与时空尺度拓展方法研究进展[J]. 农业工程学报，2015，31（6）：8－16. Zhang Baozhong， Xu Di， Liu Yu， et al. Review of multi-scale evapotranspiration estimation and spatio-temporal scale expansion[J]. Transactions of the Chinese Society of Agricultural Engineering （Transactions of the CSAE）， 2015，31（6）: 8－16. （in Chinese with English abstract）

[13] Nowicki S C， Davis H T， Scriven L E. Microscopic determination of transport parameters in drying porous media[J]. Drying Technology， 1992， 10（4）: 925－946.

[14] Prat M. Recent advances in pore-scale models for drying of porous media[J]. Chemical Engineering Journal， 2002，86（1/2）: 153－164.

[15] Vorhauer N， Tran Q T， Metzger T， et al. Experimental investigation of drying in a model porous medium: influence of thermal gradients[J]. Drying Technology， 2013， 31（8）: 920－929.

[16] Laurindo J B， Prat M. Numerical and experimental network study of evaporation in capillary porous media， drying rates[J]. Chem. Eng. Sci. 1998， 53（12）: 2257－2269

[17] Xiao Bo， Chang Jian， Huang Xiaoli， et al. A moisture transfer model for isothermal drying of plant cellular materials based on the pore network approach[J]. Drying Technology， 2014，32（9）: 1071－1081.

[18] Yiotis A G， Tsimpanogiannis I N， Stubos A K， et al. Pore-network study of characteristic periods in the drying of porous media[J]. Journal of Colloid and Interface Science，2006， 297（2）: 738－748.

[19] Prat M. On the influence of pore shape， contact angle and film flows on drying of capillary porous media[J]. International Journal of Heat and Mass Transfer， 2007，50（7/8）: 1455－1468.

[20] Xiao Zhifeng， Yang Deyong， Yuan Yuejin， et al. Fractal pore network simulation on the drying of porous media[J]. Drying Technology， 2008， 26（6）: 651－665.

[21] 王会林，卢涛，姜培学. 生物多孔介质热风干燥数学模型及数值模拟[J]. 农业工程学报，2014，30（20）：325－333. Wang Huilin， Lu Tao， Jiang Peixue. Mathematical model and numerical simulation of biological porous medium during hot air drying[J]. Transactions of the Chinese Society of Agricultural Engineering （Transactions of the CSAE）， 2014，30（20）: 325－333. （in Chinese with English abstract）

[22] Yiotis A G， Tsimpanogiannis I N， Stubos A K. Fractal characteristics and scaling of the drying front in porous media: A pore network study[J]. Drying Technology， 2010， 28（8）: 981－990.

[23] Francisco A. SanMartin Joao B. Laurindo Luis A Segura. Pore-scale simulation of drying of a porous media saturated with a sucrose solution[J]. Drying Technology， 2011， 29（8）: 873－887.

[24] 刘玲霞，刘相东，常剑，等. 果蔬干燥过程的水分跨膜传输模型构建[J]. 农业工程学报，2012，28（20）：256－264. Liu Lingxia， Liu Xiangdong， Chang Jian， et al. Transmission model of moisture transmembrane during fruit and vegetable drying process[J]. Transactions of the Chinese Society of Agricultural Engineering （Transactions of the CSAE）， 2012，28（20）: 256－264. （in Chinese with English abstract）

[25] Shaeri Mohammad Reza， Beyhaghi Saman， Pillai Krishna M. On applying an external-flow driven mass transfer boundary condition to simulate drying from a pore-network model[J]. International Journal of Heat and Mass Transfer， 2013， 57（1）: 331－344.

[26] Huang Xiaoli， Qi Tingting， Wang Zhenhua， et al. A moisture transmembrane transfer model for pore network simulation of plant materials drying[J]. Drying Technology， 2012， 30（15）: 1742－1749.

[27] 袁越锦，徐英英，刘相东. 仓内谷物通风干燥孔道网络数值模拟与验证[J]. 农业机械学报，2009，40（11）：119－123. Yuan Yuejin， Xu Yingying， Liu Xiangdong. Numerical simulation and experiment on drying of corn material in bin[J]. Transactions of the Chinese Society for Agricultural Machinery， 2009， 40（11）: 119－123. （in Chinese with English abstract）

[28] 张烨，李长友，马兴灶，等. 干燥机粮层通风阻力特性数值模拟与试验[J]. 农业机械学报，2014，45（7）：216－221. Zhang Ye， Li Changyou， Ma Xingzao， et al. Experiment and numerical simulation of layer resistance parameters in dryer[J]. Transactions of the Chinese Society for Agricultural Machinery， 2014， 45（7）: 216－221. （in Chinese with English abstract）

[29] 曹崇文，朱文学. 农产品干燥工艺过程的计算机模拟[M].北京：中国农业出版社，2000.

Multi-scale and multi-layer structural heat and mass transfer modeling and experiment on drying of rice in bin

Li Yan1, Xu Yingying1, Yuan Yueding2, Zhao Zhe1, Yuan Yuejin1
（1. College of Electricɑl ɑnd Informɑtion Engineering, Shɑɑnxi University of Science ɑnd Technology， Xi’ɑn 710021, Chinɑ; 2. College of Mɑthemɑtics ɑnd Computer Science， Yichun University， Yichun 336000， Chinɑ）

Abstract:The traditional drying theory of grain materials is mainly based on the assumption of moisture transfer in continuous medium at present， which indicates that the difference between the skeleton and pore is ignored. However， the complex structure inside grain stack is closer to a discrete solid， and the internal part of grain is a multi-layer physical structure，including seed coat （hull）， chaff and embryo tissue. Obviously， it is not consistent with the actual situation to ignore the influence of these factors on drying process. So， in order to study the mechanism of heat and mass transfer for the grain drying in bin and the effect of rice stack structure characteristics on the drying process， the basic idea of multi-scale theory was introduced to the drying research field of grain materials in this paper， and a multi-scale and multi-layer structural model of heat and mass transfer processes for grain drying was established by applying the pore network method and taking the rice in bin as the study object， of which the physical model included the pore-throat-pore network and the skeleton （grain） and the rice stack was divided into the particle scale and the dryer scale. The difference of skeleton and pore at different scale was taken into account by distinguishing the mechanism of heat and mass transfer at different scale， and the corresponding heat and mass transfer theory was applied to describe the heat and mass transfer process during the drying in rice stack porous media. The information correlation point between the 2 adjacent scales was found to fuse the corresponding heat and mass transfer information. The effect of rice stack structure characteristics on the drying process was considered by obtaining the rule of the rice packing structure transformed into the pore network and coupling the momentum， energy and mass equations. An experimental study on rice drying was conducted in order to validate this model. The drying bed of experiment was a rectangular cavity with 0.1 m thickness， 0.2 m width and 0.2 m height. There was an air inlet with the shape of isosceles right triangles at the bottom of the drying container， the top of the drying container was as air outlet open to the atmosphere， and there were 14 holes opened on the front wall of the drying container， which were for measurements of the air humidity and temperature. The simulation and experimental results indicated that the established model could explain the mechanical properties of rice drying well. The maximum relative error between the simulation results and experimental data for the average moisture content of rice stack in the container was about 7.6%， and the maximum relative error between the simulation results and experimental data for the dry basis moisture content of single grain of rice at air inlet was approximately 6.8%. During the drying process， the temperature of rice was about 2 K lower compared with the corresponding vapor temperature，and the traditional drying theory that neglected the difference between the grain skeleton and pore was inappropriate. The heat transfer rate of rice grain was much faster than the mass transfer rate and there was a higher moisture gradient inside the rice particle. The diffusion coefficient of rice embryo played an important role in the drying process， whose effect on drying was larger than that of rice hull and chaff. The migration of the moisture in the rice grain from embryo to hull surface became much more difficult when the diffusion coefficient of rice embryo was very small， and the moisture was imprisoned effectively inside the rice grain. The research results can provide a theoretical basis for the design of the process and equipment of the grain drying in bin.

Keywords:dying; models; grains; rice; multi-layer structural; multi-scale

作者简介：李艳，女，四川仁寿人，陕西科技大学副教授，主要从事工业自动化与干燥过程及控制的研究。Email：yan7205@sina.com

基金项目：国家自然科学基金项目（51276105）和陕西省科技厅科学技术研究发展计划项目（2013k07-28）资助。

收稿日期：2015-08-19

修订日期：2015-11-23

中图分类号：TQ021.4

文献标志码：A

文章编号：1002-6819（2016）-02-0258-08

doi：10.11975/j.issn.1002-6819.2016.02.037