A survey on rough set theory and its applications

Qinghu Zhng,Qin Xie,Guoyin Wng,*

aChongqing Key Laboratory of Computational Intelligence,Chongqing University of Posts and Telecommunications,Chongqing 400065,China

bSchool of Science,Chongqing University of Posts and Telecommunications,Chongqing 400065,China

A survey on rough set theory and its applications

Qinghua Zhanga,b,Qin Xiea,Guoyin Wanga,*

aChongqing Key Laboratory of Computational Intelligence,Chongqing University of Posts and Telecommunications,Chongqing 400065,China

bSchool of Science,Chongqing University of Posts and Telecommunications,Chongqing 400065,China

After probability theory,fuzzy set theory and evidence theory,rough set theory is a new mathematical tool for dealing with vague,imprecise, inconsistent and uncertain knowledge.In recent years,the research and applications on rough set theory have attracted more and more researchers' attention.And it is one of the hot issues in the artificial intelligence field.In this paper,the basic concepts,operations and characteristics on the rough set theory are introduced firstly,and then the extensions of rough set model,the situation of their applications,some application software and the key problems in applied research for the rough set theory are presented.

Rough sets;Fuzzy sets;Soft computing;Artificial intelligence;Approximation space;Extended models

1.Introduction

In the research of theory and application for information science,intelligent information processing is a hot issue. Because of the development of computer science and technology,especially the development of computer network,a large amount of information is provided for people every second of the day.With the growing amount of information, the requirement for information analysis tools is also becoming higher and higher,and people hope to automatically acquire the potential knowledge from the data.Especially in the past 30 years,knowledge discovery(rule extraction,data mining,machine learning,etc.)has attracted much attention in the field of artificial intelligence.Thus,various kinds of knowledge discovery methods came into being.

Proposed by Professor Pawlak in 1982,the rough set theory is an important mathematical tool to deal with imprecise,inconsistent,incomplete information and knowledge[1].Originated from the simple information model,the basic idea of the rough set theory can be divided into two parts.The first part is to form concepts and rules through the classification of relational database.And the second part is to discovery knowledge through the classification of the equivalence relation and classification for the approximation of the target.As a theory of data analysis and processing,the rough set theory is a new mathematical tool to deal with uncertain information after probability theory,fuzzy set theory,and evidence theory.For the fuzzy set theory,membership function is a key factor.However,the selection of membership function is uncertain.Therefore,in a sense,the fuzzy set theory is an uncertain mathematical tool to solve the uncertain problems.In rough set theory,two precise boundary lines are established to describe the imprecise concepts.Therefore,in a sense,the rough set theory is a certain mathematical tool to solve the uncertain problems.

Because of novel thinking,unique method and easy operation,the rough set theory has become an important information processing tool in the field of intelligent information processing [2,3].And it has been widely used in machine learning,knowledge discovery,data mining,decision support and analysis,etc. In 1992,the first International Workshop on rough set theory was held in Poland.And the rough set theory was considered as a new research topic in computer science by the ACM in 1995. Currently,there are four international conferences on rough sets, i.e.,RSCTC,RSFDGrC,RSKT,and IJCRS.At the same time, Chinese scholars have made a lot of achievements in this field.Since 2001,Chinese rough set and soft computing academic conference(CRSSC)has been held every year.In addition,a series of international academic conferences are held in China, such as RSFDGRC2003,IEEE GrC2005,RSKT2006, IFKT2008,RSKT2008,IEEE GrC2008,RSKT2010,etc.[4].

2.Basic concepts of rough sets

One of the main research problems of the rough sets is the approximation of sets,and the other one is the algorithms of the analysis or reasoning for related data.Some basic concepts on rough set theory are reviewed as follows.

Consider a simple knowledge representation scheme in which a finite set of objects is described by a finite set of attributes.Formally,it can be defined by an information system S expressed as the 4-tuple[5].

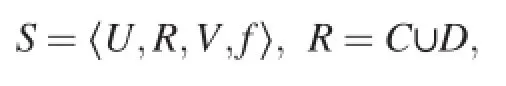
whereUis a finite nonempty set of objects,Risa finite nonempty setof attributes,the subsetsCandDare called condition attribute set and decision attribute set,respectively.whereVais the set of values of attributea,and card(Va)＞1, andf:R→Vis an information or a description function.

In Table 1U={x1,x2,…,x6}is a finite nonempty set,also called a universe,andR={Headache,Myalgia,Temperature,Flu}is a finite nonempty set,also called an attribute set.

Definition 1.(Indiscernible relation)[5]Given a subset of attribute setB⊆R,an indiscernible relationind(B)on the universeUcan be defined as follows,

The equivalence relation is an indiscernible relation.And the equivalence class of an objectxis denoted by[x]ind(B),or simply[x]Band[x],if no confusion arises.The pair (U,[x]ind(B))is called an approximation space.

Definition 2.(Upper and lower approximation sets)[5] Given an information systemS=〈U,R,V,f〉,for a subsetX⊆U,its lower and upper approximation sets are defined, respectively,by

where[x]denotes the equivalence class ofx.

Table 1 An information table[5].

The family of all equivalence classes is also known as the quotientsetofU,and itis denoted byU/R={[x]|x∈U}.The universe can be divided into three disjointregions,namely,the positive,boundary and negative regions[6],

If an objectx∈POS(X),then it belongs to target setXcertainly.

If an objectx∈BND(X),then it doesn'tbelong to targetsetXcertainly.

If an objectx∈NEG(X),then it cannot be determined whether the objectxbelongs to target setXor not.

Definition 3.(Definable sets)[5]Given an information systemS=〈U,R,V,f〉,for any target subsetX⊆Uand attribute subsetB⊆R,if and only ifXis called a definable set with respect toB.

Definition 4.(Rough Sets)[5]Given an information systemS=〈U,R,V,f〉,for any target subsetX⊆Uand attribute subsetB⊆R,if and only ifXis called a rough set with respect toB.

A rough set and its three disjoint regions are shown as Fig.1.

The uncertainty of a rough set is caused by its boundary region.The larger the boundary region is,the greater the degree of uncertainty will be.The uncertainty of a rough set can be measured by the roughness.

Definition 5.(Roughness of rough sets)[5]Given an information systemS=〈U,R,V,f〉,for any target subsetX⊆Uand attribute subsetB⊆R,the roughness of setXwith respect toBcan be defined as follows,

where,X≠φ(IfX=φ,thenPB(X)=0);|·|denotes the cardinality of a finite set.

Proposed by professor Zadeh[7],soft computing(SC)is one of key intelligent system technologies in the future,and it has been researched and applied in solving various practical problems extensively.The guiding principle of soft computing is to allow the imprecise,uncertain or some real approximate solutions to replace the exact solutions of an original problem.So,a solution with strong robustness and low cost can be established to coordinate with the real systems better[8].

3.Basic operations of rough sets[9]

Fig.1.A rough set in rough approximation space.

where～Xis an abbreviation forU-X.

De Morgan's laws have the following counterparts[1]:

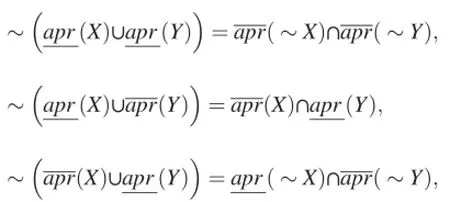
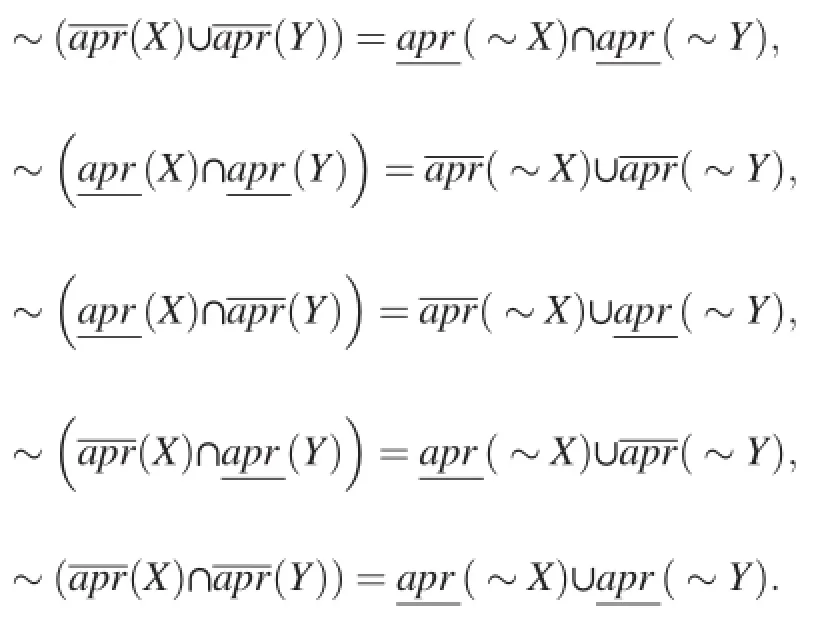
IfX⊆Y,then

In addition,it is obviously that following operations can be gotten,

As a typical soft computing method,rough set theory has been developed and applied rapidly since it was put forward. Some characteristics of the theory are shown as follows,

(1)The mathematical structure of rough set is mature,and it doesn't need any prior knowledge;

(2)The rough set model is simple,and it is easy to be calculated;

(3)Including imprecise,incomplete and fuzzy data,various types of data can be processed by rough set model;

(4)By rough set model,minimum expression(the simplest reduction,the attribute core,etc.)of the knowledge can be obtained,and an approximate description for an uncertain concept can be described in different granularity levels;

(5)The precise and simplified rules can be produced by rough sets,and they can be applied to intelligent controls.

Based on the above characteristics,there are three distinctions between rough set theory and other uncertainty theories.Firstly,for the rough set theory,the priori in formation of data doesn't need to be provided except the data.Secondly,the rough set theory is relatively objective to describe and deal with uncertainty.Finally,the rough set theory has strong complementary with probability theory,fuzzy mathematics, evidence theory and other uncertainty theories or methods.

The classical rough set model can only process discrete data.However,in real life,many data are continuous.Thus, how to deal with real data by rough set model is still a valuable research issue in the future.

4.Several extensions of rough set model

The extensions of rough set model are the important research direction of rough set theory.Combining the rough set theory with other theoretical methods or technologies,a large number of research results on extensions have emerged. Several typical extensions will be reviewed in this section. And the extended definition of the upper approximation set and the lower approximation set will be given firstly in this section,and then several extended models will be introduced.

4.1.Probabilistic rough sets

Based on the classical rough set theory,the lower approximation set requires that the equivalence class is a subset of the target set,for the upper approximation set,the equivalence class must have a non-empty overlap with the target set.Thus, the classical rough set theory does not allow any uncertainty, in other words,the main limitation of the classical rough sets is lack of error tolerance.In order to overcome this shortcoming,Wong and Ziarko[6,10]brought the probability approximation space into the rough set theory in 1987.

Based on the notions of rough membership functions[11] and rough inclusion[12],approximation sets of probabilistic rough sets can be formulated.Both notions can be interpreted in terms of conditional probabilities or posteriori probabilities. Suppose Pr(X|[x])is the conditional probability of an object belonging to the target setXgiven that the object belongs to [x].This probability may be simply estimated asdenotes the cardinality of a finite set[13,14].In terms of conditional probability,the three disjoint regions of the classical rough sets can be equivalently defined by[10].

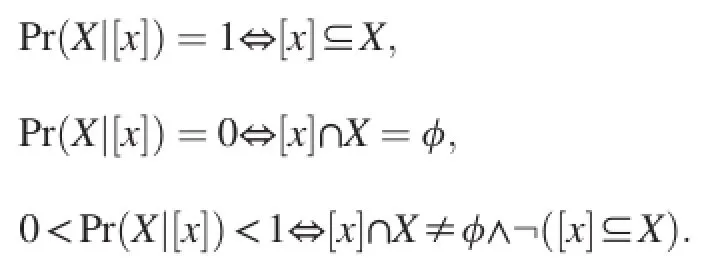
The three disjoint regions of the classical rough sets can also be expressed as follows,

According to the different probability approximation formulas and the different interpretations of the required parameters,the probabilistic rough set model has three typical extended models.The three probabilistic models have been proposed and studied intensively.They are the decision theoretic rough set model[15-17],the variable precision rough set model[18,19],and the Bayesian rough set model [20,21].

The decision-theoretic rough set model and the variable precision rough set model are introduced in the next section.

4.1.1.Decision-theoretic rough set model

Based on the classical rough set model,the decisions of acceptance and rejection are made withoutany error.However, the probabilistic rough set model allows the tolerance of inaccuracy in lower and upper approximation sets,or equivalently in the probabilistic positive,boundary and negative regions.

The probability of two extreme values,namely 0 and 1,are used in three regions of the classical rough set model.Inspired by this,the decision-theoretic rough set model is proposed by Yao[17].In this model,the values 0 and 1 mentioned ahead are replaced by a pair of probabilistic thresholdsα,β. Considering two limiting conditions,0≤β＜α≤1,0≤α, β≤1,three disjoint regions with two probabilistic thresholds are shown as follows,

Obviously,the unit interval[0,1]of probability values are divided into three regions,namely,the acceptance region [α,1],the rejection region[0,β],and the deferment region (α,β).

Let the two probabilistic thresholds beα=1,β=0,the decision-theoretic rough set model just degrades to the classic rough set model.Therefore,from the formal perspective, positive,negative and boundary regions with two thresholds are the extensions compared to the theory of the classical rough sets.

For the construction of a new model,the basic concepts, basic quantities and semantic interpretation of the model need to be explored and explained.

There are at least three problems need to be solved for the probabilistic rough set model shown as follows[22],

(1)How to interpret and calculate the thresholds.

(2)How to estimate the conditional probability Pr(X|[x]).

(3)How to interpret and apply positive,negative and boundary regions with probability thresholds.

For the decision-theoretic rough set model,the solutions to the above three problems are shown as follows[23],

(1)Based on the well-established Bayesian decision procedure,for defining the three disjoint regions,systematic methods for deriving the required probabilistic thresholds α,βon probabilities are provided by the decision-theoretic rough set model.

(2)An easy method can be obtained to evaluate the conditional probabilities by the Naive Bayesian rough set model proposed by Yao and Zhou[24].

(3)The three-way decision theory can be considered as the application of the three regions of the model.

The contribution of the decision-theoretic rough set model lies in that it not only gives the results of probability positive, negative and boundary regions,the more important is that a reasonable solution to solve the three problems mentioned ahead is given.Therefore,the decision-theoretic rough set model is a practical model with a solid theoretical foundation.

4.1.2.Variable precision rough set model

The rough set theory has been widely used in dealing with data classification problems.However,the classical rough set model is quite sensitive to noisy data.To deal with noisy data and uncertain information,the variable precision rough set model was proposed by Ziarko[19]in 1993.

In this model,based on degree of data noise,a probabilistic thresholdβwas defined.And the value range of this probabilistic threshold is the interval[0,0.5).Considering the mentionedβ,three disjoint regions are shown as follows,

(1)β-positive region:POSβ(X)=

{x∈U|Pr(X|[x])≥1-β};

(2)β-negative region:NEGβ(X)={x∈U|Pr(X|

[x])≤β};

(3)β-boundary region:BNDβ(X)

={x∈U|β＜Pr(X|[x])＜1-β}.

Definition 6.The degree of correlation between the equivalence class[x]and the target setXis defined as follows,

Kβ([x],X)denotes the proportion that the samples on universeUdivided intoβ-positive region andβ-negative region roughly or definitely.

4.2.Rough set model based on tolerance relation

The equivalence relation in the classical rough set theory must satisfy reflexivity,symmetry and transitivity.If the transitivity can't be satisfied in an equivalence relation,the equivalence relation will be replaced with the tolerance relation[25].Research shows that based on the traditional in discernibility relation,the rough set theory is unable to deal with incomplete information systems.Thus,the classical rough set theory model needs to be extended so that it can deal with the incomplete information system.In this section,the new extension based on tolerance relation is shown as follows.

LetS=〈U,R,V,f〉be an information system,thenull valuewill be denoted by‘*’for the missing property value in the attribute subset(B⊆R).

Definition 7.[5,25]The tolerance relationTis defined as follows,

Obviously,Tis reflexive and symmetric,but not necessarily transitive.IB(x)denotes the tolerance class of objectx.Based on the definition of tolerance class,the upper approximation set and the lower approximation set of the target setXon attribute subsetB⊆Rcan be defined in the incomplete information system.

Definition 8.[5]Given an incomplete information systemS=〈U,R,V,f〉,the definitions of the upper approximation setand the lower approximation set

4.3.Multi-granulation rough set model

Nowadays,in the research of multi-granulation rough sets, there have been many achievements[26-29].It has been widelyused in various fields.In 2010,Qian[31]proposes multi granulation rough set model(MGRS)to extend classical rough set model for the first time.The approximation sets of target setXcan be discussed by two equivalence relations,firstly.

Definition 9.[31]LetS=＜U,R,V,f＞be a complete information system,P,Q⊆Rbe two subsets of the attributes, andX⊆U.The lower and upper approximation sets ofXon universeUare defined as follows,

Then,the approximation sets ofXcan be defined by multi equivalence relations on the universe.

Definition 10.[31]LetS=＜U,R,V,f＞be a complete information system,P1,P2,…,Pm⊆Rbemsubsets of the attributes,and∀X⊆U.The lower and upper approximation sets ofXare defined as follows,

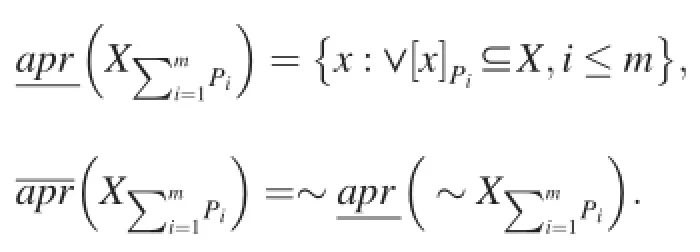
If the multi-granulation rough set model is constructed, compared with classical rough set model,the smaller lower approximation and bigger upper approximation sets will be obtained.From the view of decision-making,foran optimistic decision is made by an obtained rule.So this model is called the optimistic rough set model on multi-granulation rough set theory.In addition,the other model called the pessimistic multi-granulation rough set model is also defined by Qian[32].

Definition 11.[33]LetS=＜U,R,V,f＞be a complete information system,P,Q⊆Rbe two subsets of the attributes, and∀X⊆U.The pessimistic lower and upper approximation sets ofXonUare defined as follows,

Definition 12.[30,33]LetS=＜U,R,V,f＞be a complete information system,P1,P2,…,Pm⊆Rbemsubsets of the attributes,and∀X⊆U.The pessimistic lower and upper approximation sets of X are defined as follows,

From the view of decision-making,a rule which is obtained by the lower approximation set of pessimistic rough sets will lead to a pessimistic decision.So this model is called the pessimistic rough set model on multi-granulation rough set.

The difference between classical rough set model and MGRS is shown in Fig.2[32].

In Fig.2,the bias region is the lower approximation setofXobtained by a single granulationP∪Q,which is expressed by the equivalence classes in the quotient setU/(P∪Q).And the shadow region is the lower approximation set ofXinduced by two granulationsP+Q,which is characterized by the equivalence classes in the quotient setU/Pand the quotient setU/Qtogether.

4.4.Game-theoretic rough set model[34,35]

Defined by probabilistic rough set theory,the positive, negative and boundary regions are associated with three certain levels of uncertainty.In these regions,the uncertainty levels are determined by a pair of threshold values.A critical problem is the determination of optimal values of these thresholds.The problem may be investigated by considering a possible relationship between changes in probabilistic thresholds and their impacts on uncertainty levels of different regions.The game-theoretic rough set(GTRS)model is investigated in exploring such a relationship.

For analyzing and making intelligent decisions,when multiple conflicting criteria are involved,the GTRS model is applicable.The process of determining probabilistic thresholds with this model will be reviewed as follows.

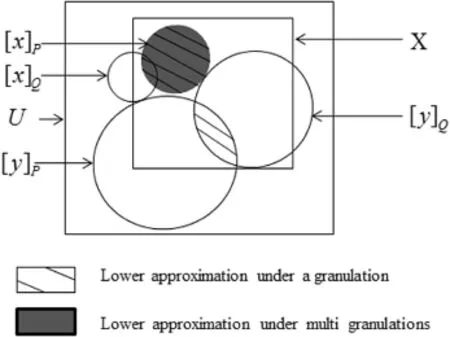
Fig.2.MGRS model[32].

For calculating probabilistic thresholds with the context of probabilistic rough sets,the GTRS model provides a game theoretic setting.For players in a game,in terms of changes to probabilistic thresholds,the model formulates strategies of players by realizing multiple criteria.Each player will configure the thresholds in order to maximize his benefits. When strategies are played together and considered as a strategy profile,the individual changes in thresholds are incorporated to obtain a threshold pair.This means that eachstrategy profile of the form(s1,s2,...,sn)is associated with a threshold pair(α,β).

The model requires that the game be formulated such that each player represents the region parametersαorβ.The actions all players choose are summarized in Table 2.They either increase or decrease their actual probabilistic values by a small increment or decrement respectively.This will result in equivalence classes from the boundary region moving to either the positive region(decrease ofα)ornegative region(increase ofβ).

For the game between two individuals,the final outcome will always reach Nash equilibrium.Namely,none of the players can benefit by changing their respective strategies. Thus,through this model,the optimal thresholds of probability rough sets can be gotten.

5.Theory and application on rough sets

Based on rough set theory,application research mainly focuses on attribute reduction,rule acquisition,intelligent algorithm,etc.Attribute reduction as a NP-Hard problem has been carried out a systematic research.Based on rough set model,the development of reduction theory provides a lot of new methods for data mining.For example,in the different information systems(coordinated or uncoordinated,complete or incomplete),with information entropy theory,concept lattice and swarm intelligence algorithm,the rough set theory has gained the corresponding achievements.At present,the research is mainly concentrated on three aspects,such as theory,application and algorithm.

(1)The theoretical research

·Research on algebraic structure of rough sets with abstract algebra[36-39].

·Describing rough approximation space with topology [40-43].

·Combining rough set theory with other soft computing methods or artificial intelligence methods[5,44-48].

·Extending classical rough set model to generalized rough set model[49-51],namely,equivalence relations are extended to similar relations or general binary relations.

·Rough set models based on data distribution[52-56], such as the probabilistic rough setmodel,the decision theoretic rough set model,the cloud rough set model, etc.

Table 2 The strategy scenario for decreasing the boundary region(winner-take-all) [34].

·Rough set models based on multi-granularity [32,33,56-63].

·Optimal approximation sets of a target concept [64,65].

(2)The application research

(a)Application of the rough sets in fault diagnosis.

·The medical diagnosis[47,66-68].

·Power system and other industry for fault diagnosis[69-72].

·Prediction and control[73-75].

·Pattern recognition and classification[76,77].

(b)Application of the rough sets in image processing.

·Intelligent emotion recognition[78].

·Remote sensing image processing[79].

·Image segmentation,enhancement and classification[80,81].

(c)Application of the rough sets in massive data processing.

·Analyzing data of gene expression[82].

·Intrusion detection[83,84].

·Intelligence analysis[85].

(d)Application of the rough sets in intelligent control system.

·Intelligent dispatching[86,87].

·E-mail filtering[88].

(3)The algorithm research

(a)Heuristic algorithm on attribute reduction and rule extraction.

·The study based on attribute significance[89].

·Incorporating the heuristic algorithm based on information metric[90,91].

·The integrating with parallel computing[92].

(b)Combining the rough sets with other computational intelligence algorithm.

·Combining with neural network algorithm.It is used to preprocess data for improving the convergence speed of neural network[93].

·Combining with support vector machine(SVM) [94].

·Deriving the rough set models from the cloud models[80].

·Combining with genetic algorithm and Particle Swarm Optimization algorithm(PSO)[80,95].

6.The related software of rough set theory

As the development of the rough sets,some software applied to data analysis are beginning to emerge.At present, some institutions and individuals have exploited pieces of useful software about the rough sets.For example,for knowledge discovery in database,Data Logic R is exploited by Reduct System Inc in Canada.The software is programmed by the C language,and it can be used in the field of science research,industry service,etc.LERS(learning from Examp on Rough Sets)is exploited by the University of Texas in theUnited States.And it can extractrules from a large number of complex data.LERS has been adopted by NASA's Johnson Space Center as a development tool for expert system.And it also has been adopted by a project funded by United States Environmental Protection Agency.Rough DAS system is exploited at Poznan University of Technology.RIDAS system is exploited by Wang,etc.who are from Chongqing University of Posts and Telecommunications[96].In addition,ICE(Info bright Community Edition)is exploited by Dominik,etc.The development of above software promotes development and application of the rough set theory.

7.Academic activities on the rough sets

In the last thirty years,the development of rough set theory has gotten a good result whether in the theoretical research or applied research.In recent years,an increasing number of academic activities on rough sets have been held.Athome and abroad,a range of academic conferences promote the development of rough set theory.With academic and applied value, a number of papers are published.It makes academic communication convenient,and also promotes the development and application of the rough sets.A list of the representative academic activities is shown as follows,

·In 1992,the first International Workshop on rough set theory was held in Poland.In 1993,there were 15 papers published inFoundation of computing and decision science;

·In 1993-1994,the second and the third International Workshop on rough set theory was held in Canada and America,respectively;

·In 1995,Rough Setswas published inACM Communicationsby Pawlak,etc.It greatly expanded the international influence of the theory;

·In 1996-1999,in Japan and the United States,the 4th to 7th International Workshop on rough set theory was held, respectively.

·Since 1998,RSCTC has been held every even-numbered year,RSFGrC has been held every odd-numbered year;

·Since 2005,IEEE GrC has been held every year.

·Since 2006,RSKT has been held every year.

·In 2007,the first session of IJCRS was held,and itwas reestablished in 2012.Then since 2012,it has been held every year.

In China,the rough set theory has been developed rapidly, and academic activities are also very active.

·In 2003,CRSSC was established.

·Since 2001,CRSSC has been held every year.

·Since 2007,CGrC and CWI have been held every year.

8.Outlook of rough set theory and its applications

At present,research for rough sets has achieved fruitful results,but rough set theory is still a valuable research problem.As the founder of the rough set theory,Pawlak, interpreted that:some problems forrough set theory need to be solved,such as rough logic,rough analysis,etc.

Rough set theory is confronted with some new problems in the process of its development.For example,the generalization ability of rough sets needs to be improved,and the probability distribution of sample data needs to be further considered.To sum up,the main problems that need to be further concerned in the future are shown as follows,

(1)Extensions of equivalence relation.The strict equivalence relation should be replaced with the general binary relations,such as order relation,tolerance relation,and similarity relation.

(2)Improvements of the generalization ability of rough sets. Based on the data information system,the existing rough set theory does not consider the problem about probability distribution of the data samples.Moreover,in the process of training sample sets,attribute reduction would lead to over-fitting problem.

(3)Research on rough logic.Based on the rough set theory, the rough logic and its deduction theory system can be established.And combining with probability logic, random truth degree of rough logic can be studied in the future.

(4)Granular computing based on rough set theory.Several extended models need to be further studied,such as multi granulation rough set model,variable multi-granularity rough set model,dynamic rough set model,etc.

(5)Research on random rough sets models.Rough set theory describes vagueness(uncertainty)in decision information systems,but the problem is still lack of research. Combining rough sets with cloud model may be an effective way to solve this problem.

(6)3DM[97](Data-driven Data Mining Domain-oriented).1 Encoding prior domain knowledge,user's interest and constraint for a specific task and user's control.2 Designing an incremental method that could take data, prior domain knowledge,user's interest,user's constraint, user's control together as its input.3 Applying our incremental mining method to real-world data mining task, such as instance financial data mining in capital markets.

(7)Research on the fusion of rough sets and various soft computing methods.For example,the combination of rough sets and neural network accelerates the convergence speed of neural network.In order to deal with large data sets conveniently,combining rough sets and genetic algorithm forms a hybrid intelligent system.

(8)The interaction among attributes.The interaction among redundant attributes may have a profound effect on the expression and resolution of problems.

(9)Rough sets and three-way decisions[98].To fully understand and appreciate the value and power of three-way decisions,we may look into fields where the ideas of three-way decisions have been used either explicitly or implicitly.In one direction,one can adoptideas from these fields to three-way decisions.In the other direction,we canapply new results of three-way decisions to these fields. We can cast a study of three-way decisions in a wider context and extend applications of three-way decisions across many fields.In the next few years,we may investigate three-way decisions in relation to interval sets[99], three-way approximations of fuzzy sets[7,100],shadowed sets[101],orthopairs[102-104],squares of oppositions [105-107],granular computing[108,109],multilevel decision-making[110],etc.

9.Conclusions

The rough set theory has been researched for more than thirty years.And it has made many achievements in many fields,such as machine learning,knowledge acquisition,decision analysis,knowledge discovery in database,expert system,decision support system,inductive inference,conflict resolution,pattern recognition,fuzzy control,medical diagnostics applications and so on.And for research on granular computing,it has become one of the main models and tools. The application prospect of rough set theory is very broad.The rough sets not only can be used to deal with new uncertain information systems,butalso can optimize many existing soft computing methods.For the rough set theory,in the process of data mining,there are still a large number of problems need to be discussed,such as large data sets,efficient reduction algorithm,parallel computing,hybrid algorithm,etc.

Acknowledgments

This work has been supported by the National Key Research and Development Program of China under grant 2016YFB1000905,the National Natural Science Foundation of China under Grant numbers of 61272060,61472056 and 61572091.

[1]Z.Pawlak,Rough set[J],Int.J.Comput.Inf.Sci.11(5)(1982).

[2]Z.Pawlak,Inf.Sci.147(1-4)(2002)1-12.

[3]T.Li,H.S.Nguyen,G.Y.Wang,et al.,Rough Sets and Knowledge Technology,Springer Berlin Heidelberg,2012.

[4]G.Y.Wang,Y.Y.Yao,H.Yu,Chin.J.Comput.32(7)(2009) 1229-1246.

[5]G.Y.Wang,Rough Set Theory and Knowledge Discovery,Xi'an Jiaotong University Press,Xi'an,China,2001.

[6]Y.Y.Yao,S.Greco,R.Słowi′nski,Probabilistic rough sets.Springer Handbook of Computational Intelligence,2015,pp.387-411.

[7]L.A.Zadeh,Inf.Control 8(3)(1965)338-353.

[8]Q.H.Zhang,Research on Hierarchical Granular Computing Theory and its Application,Southwest Jiaotong University,Chengdu,China,2009.

[9]G.Y.Wang,D.Q.Miao,W.Z.Wu,J.Y.Liang,J.Chongqing Univ.Posts Telecommun.(Natural Science Edition)22(5)(2010)541-544.

[10]S.K.M.Wong,W.Ziarko,Fuzzy Sets Syst.21(3)(1987)357-362.

[11]Z.Pawlak,A.Skowron,Rough membership functions.Advances in Dempster-Shaefer Theory of Evidence,John Wiley&Sons,Inc,1994.

[12]L.Polkowski,A.Skowron,Int.J.Approx.Reason.15(4)(1996) 333-365.

[13]D.Liu,T.R.Li,R.Da,Inf.Sci.181(181)(2011)3709-3722.

[14]Z.Pawlak,A.Skowron,Inf.Sci.177(1)(2007)3-27.

[15]Y.Y.Yao,Information granulation and approximation in a decisiontheoretical model of rough sets.Rough-neural Computing,Springer Berlin Heidelberg,2004,pp.491-516.

[16]Y.Y.Yao,Expert Syst.20(5)(2003)287-297.

[17]Y.Y.Yao,S.K.M.Wong,et al.,Int.J.Man-Machine Stud.37(6)(1992) 793-809.

[18]J.D.Katzberg,W.Ziarko,Variable precision rough sets with asymmetric bounds,in:International Workshop on Rough Sets and Knowledge Discovery:Rough Sets,Fuzzy Sets and Knowledge Discovery, Springer-Verlag,1993,pp.167-177.

[19]W.Ziarko,J.Comput.Syst.Sci.46(1)(1993)39-59.

[20]D.Slezak,W.Ziarko,Int.J.Approx.Reason.40(40)(2005)81-91.

[21]S.Greco,B.Matarazzo,R.Słowi′nski,Rough membership and bayesian confirmation measures for parameterized rough sets.Rough Sets,Fuzzy Sets,Data Mining,and Granular Computing,Springer Berlin Heidelberg,2005,pp.285-300.

[22]H.X.Li,X.Z.Zhou,T.R.Li,et al.,Decision-theoretic Rough Sets Theory Sets Theory and its Application,Science Press,Beijing,China, 2011.

[23]H.Yu,G.Y.Wang,Y.Y.Yao,Chin.J.Comput.08(2015)1628-1639.

[24]Y.Y.Yao,B.Zhou,Naive bayesian rough sets,in:Rough Set and Knowledge Technology-International Conference,Rskt 2010,Beijing, China,October 15-17,2010.Proceedings,2010,pp.719-726.

[25]M.Kryszkiewicz,Inf.Sci.112(1-4)(1998)39-49.

[26]W.H.Xu,Q.R.Wang,X.T.Zhang,Soft Comput.Fusion Found. Methodol.Appl.17(7)(2013)1241-1252.

[27]W.H.Xu,Q.R.Wang,S.Q.Luo,J.Intell.Fuzzy Syst.Appl.Eng. Technol.26(3)(2014)1323-1340.

[28]G.P.Lin,J.Y.Liang,Y.H.Qian,Inf.Sci.314(2015)184-199.

[29]W.H.Xu,Y.T.Guo,Knowledge-Based Syst.105(2016)190-205.

[30]W.H.Xu,Q.R.Wang,X.T.Zhang,Int.J.Fuzzy Syst.13(4)(2011) 246-259.

[31]Y.H.Qian,J.Y.Liang,Y.Y.Yao,etal.,Inf.Sci.180(6)(2010)949-970.

[32]Y.H.Qian,J.Y.Liang,C.Y.Dang,Syst.Man Cybern.Part A Syst. Humans IEEE Trans.40(2)(2010)420-431.

[33]Y.H.Qian,J.Y.Liang,et al.,J.Zhejiang Ocean Univ.Nat.Science 29 (5)(2010)440-449.

[34]J.P.Herbert,J.T.Yao,Fundam.Inf.108(3-4)(2011)267-286.

[35]N.Azam,J.T.Yao,Int.J.Approx.Reason.55(1)(2014)142-155.

[36]F.Zhu,C.H.He,Chin.J.Comput.23(3)(2000)330-333.

[37]S.Greco,B.Matarazzo,R.Słowi′nski,Algebraic structures for dominance based rough set approach,in:International Conference on Rough Sets and Knowledge Technology,Springer-Verlag,2008,pp.252-259.

[38]G.Cattaneo,D.Ciucci,Trans.Rough Sets II 3135(2004)208-252.

[39]G.L.Liu,W.Zhu,Inf.Sci.178(21)(2008)4105-4113.

[40]E.F.Lashin,A.M.Kozae,A.A.Abo Khadra,et al.,Int.J.Approx. Reason.40(1)(2005)35-43.

[41]W.Z.Wu,The relationship between topological spaces and rough approximation operators,in:1stPan Pacific International Conference on Topology and Applications,2015.

[42]K.Y.Qin,Z.Pei,Fuzzy Sets Syst.151(3)(2014)601-613.

[43]E.A.Abo-Tabl,Int.J.Mach.Learn.Cybern.4(5)(2013)451-458.

[44]Y.M.Chen,D.Q.Miao,R.Z.Wang,Pattern Recognit.Lett.31(3) (2010)226-233.

[45]W.H.Xu,W.X.Zhang,Fuzzy Syst.Math.20(6)(2006)115-121.

[46]W.X.Zhang,W.Z.Wu,J.Y.Liang,Theory and Method on Rough Set, Science Press,Beijing,China,2001.

[47]P.R.K.Varma,V.V.Kumari,S.S.Kumar,Int.J.Intell.Syst.Technol. Appl.14(3-4)(2015)330-353.

[48]D.P.Acharjya,L.Ezhilarasi,Int.J.Comput.Science Issues 8(2) (2011).

[49]J.Hu,G.Y.Wang,Q.H.Zhang,J.Softw.21(5)(2010)968-977.

[50]D.Liang,D.Liu,W.Pedrycz,et al.,Int.J.Approx.Reason.54(8) (2013)1087-1106.

[51]D.′Sle,W.Ziarko,Int.J.Approx.Reason.40(1)(2005)81-91.

[52]W.Ziarko,Int.J.Approx.Reason.49(2)(2008)272-284.

[53]Y.Y.Yao,B.X.Yao,Inf.Sci.200(1)(2012)91-107.

[54]Y.Y.Yao,Int.J.Approx.Reason.49(2)(2008)255-271.

[55]Y.Y.Yao,Inf.Sci.181(6)(2011)1080-1096.

[56]R.Raghavan,B.K.Tripathy,Adv.Appl.Science Res.2(3)(2011) 536-543.

[57]G.Y.Wang,Q.H.Zhang,et al.,Chin.J.Comput.31(9)(2008) 1588-1598.

[58]Q.H.Zhang,Q.Zhang,G.Y.Wang,Int.J.Approx.Reason.77(2016) 38-54.

[59]Y.H.Qian,H.Zhang,Y.L.Sang,et al.,Int.J.Approx.Reason.55(1) (2014)225-237.

[60]Y.Y.Yao,Y.H.She,Inf.Sci.327(C)(2016)40-56.

[61]M.A.Geetha,D.P.Acharjya,N.Iyengar,Algebraic properties and measures of uncertainty in rough set on two universal sets based on multi-granulation,in:Proceeding of the 6th ACM India Computing Convention.ACM,2013,p.24.

[62]X.P.Kang,D.Q.Miao,Knowledge-Based Syst.102(2016)103-115.

[63]W.Xu,C.Wu,X.B.Yang,Appl.Res.Comput.30(6)(2013) 1712-1715.

[64]Q.H.Zhang,G.Y.Wang,Y.Xiao,J.Softw.23(7)(2012)1745-1759.

[65]Q.H.Zhang,Y.B.Xue,G.Y.Wang,J.Softw.27(2)(2016)295-308.

[66]D.M.A.Saleem,D.P.Acharjya,A.Kannan,et al.,Int.J.Bioinforma. Res.Appl.8(5-6)(2012)417-435.

[67]B.K.Tripathy,D.P.Acharjya,V.Cynthya,Int.J.Artif.Intell.Appl.2(2) (2011).

[68]Z.G.Qin,Z.Y.Mao,Z.Z.Deng,J.South China Univ.Technol.28(4) (2000)30-34.

[69]V.Muralidharan,V.Sugumaran,Measurement 46(9)(2013) 3057-3063.

[70]E.H.T.Francis,L.X.Shen,Eng.Appl.Artif.Intell.16(1)(2003) 39-43.

[71]S.Rawat,A.Patel,J.J.Celestino,etal.,Artif.Intell.Rev.(2016)1-23.

[72]X.Q.Chen,J.M.Liu,Y.W.Huang,etal.,High.Volt.Eng.38(6)(2012) 1403-1409.

[73]A.I.Dimitras,R.Slowinski,R.Susmaga,et al.,Eur.J.Oper.Res.114 (2)(1999)263-280.

[74]L.X.Shen,H.T.Loh,Decis.Support Syst.37(4)(2004)583-597.

[75]A.K.Choudhary,J.A.Harding,M.K.Tiwari,J.Intell.Manuf.20(5) (2009)501-521.

[76]A.E.Hassanien,A.Abraham,J.F.Peters,et al.,IEEE Trans.Inf. Technol.Biomed.Publ.IEEE Eng.Med.Biol.Soc.13(6)(2009) 955-968.

[77]R.W.Swiniarski,A.Skowron,Pattern Recognit.Lett.24(6)(2003) 833-849.

[78]A.E.Hassanien,G.Schaefer,A.Darwish,Computational intelligence in speech and audio processing:recent advances.Soft Computing in Industrial Applications,Springer Berlin Heidelberg,2010,pp.303-311.

[79]S.K.Pal,P.Mitra,IEEE Trans.Geosci.Remote Sens.40(11)(2002) 2495-2501.

[80]P.Roy,S.Goswami,S.Chakraborty,etal.,Int.J.Rough Sets Data Anal. (IJRSDA)1(2)(2014)62-74.

[81]P.Mojon,E.B.Hawbolt,M.I.Macentee,et al.,J.Dent.Res.71(9) (1992)1633-1639.

[82]D.Slezak,Rough Sets and Few-objects-many-attributes Problem:the Case Study of Analysis of Gene Expression Data Sets,IEEE,2007,pp. 497-500.

[83]F.Hu,G.Y.Wang,Chin.J.Comput.30(8)(2007)1429-1435.

[84]A.Zainal,M.A.Maarof,S.M.Shamsuddin,Feature selection using rough set in intrusion detection,in:TENCON 2006.2006 IEEE Region 10 Conference,IEEE,2006,pp.1-4.

[85]Z.Y.Zhou,G.Z.Shen,Inf.Stud.Theory Appl.35(9)(2012)61-65.

[86]M.H.Wang,China Railw.Science 25(4)(2004)103-107.

[87]D.Chen,Y.H.Li,Q.F.Zhang,S.W.Gao,Chin.Railw.07(2009)44-46.

[88]N.P′erez-Díaz,D.Ruano-Ord′as,J.R.M′endez,et al.,Appl.Soft Comput.12(11)(2012)3671-3682.

[89]E.Flores,Int.J.Comput.Science Inf.Technol.XVII(3)(2012) 3942-3947.

[90]A.Azadeh,M.Saberi,R.T.Moghaddam,et al.,Expert Syst.Appl.38 (3)(2011)1364-1373.

[91]J.G.Bazan,H.S.Nguyen,S.H.Nguyen,et al.,Rough setalgorithms in classification problem.Rough Set Methods and Applications:New Developments in Knowledge Discovery in Information Systems,2000, pp.49-88.

[92]L.Floría,Int.J.Prod.Res.48(24)(2010)7371-7393.

[93]A.Skowron,Z.Suraj,J.Intell.Inf.Syst.7(1)(1996)5-28.

[94]Y.T.Xu,C.M.Liu,Neural Comput.Appl.22(6)(2013)1077-1084.

[95]Misinem,A.A.Bakar,A.R.Hamdan,et al.,A Rough set outlier detection based on Particle Swarm Optimization,in:International Conference on Intelligent Systems Design and Applications,Isda 2010, November 29-December 1,2010,Cairo,Egypt,2010,pp.1021-1025.

[96]G.Y.Wang,Z.Zheng,Y.Zhang,RIDAS-a rough set based intelligent data analysis system,in:International Conference on Machine Learning &Cybernetics,2002,pp.646-649.

[97]G.Y.Wang,Y.Wang,Fundam.Inf.90(4)(2009)395-426.

[98]Y.Y.Yao,Rough sets and three-way decisions,in:International Conference on Rough Sets and Knowledge Technology,Springer International Publishing,2015,pp.62-73.

[99]Y.Y.Yao,Interval-set algebra for qualitative knowledge representation, in:International Conference on Computing and Information,1993. Proceedings ICCI'93,Fifth International Conference,IEEE,1993,pp. 370-374.

[100]X.F.Deng,Y.Y.Yao,Inf.Sci.279(2014)702-715.

[101]W.Pedrycz,IEEE Trans.Syst.Man Cybern.Part B Cybern.Publ.IEEE Syst.Man Cybern.Soc.28(1)(1998)103-109.

[102]N.Vernet,C.Dennefeld,C.Rochette-Egly,et al.,Fundam.Inf.108 (3-4)(2011)287-304.

[103]D.Ciucci,Orthopairs in the 1960s:historicalremarks and new ideas,in: International Conference on Rough Sets and Current Trends in Computing,Springer International Publishing,2014,pp.1-12.

[104]D.Ciucci,D.Dubois,J.Lawry,Int.J.Approx.Reason.55(9)(2014) 1866-1889.

[105]D.Ciucci,D.Dubois,H.Prade,Oppositions in rough set theory,in: International Conference on Rough Sets and Knowledge Technology, 2012,pp.504-513.

[106]D.Dubois,H.Prade,Logica Universalis 6(1-2)(2012)149-169.

[107]Y.Y.Yao,Fundam.Inf.127(1-4)(2013)49-64.

[108]Y.Y.Yao,Granular computing and sequential three-way decisions,in: International Conference on Rough Sets and Knowledge Technology, Springer Berlin Heidelberg,2013,pp.16-27.

[109]Q.H.Zhang,Y.Xiao,J.Inf.Comput.Science 8(3)(2011)385-392.

[110]G.Q.Zhang,J.Lu,Y.Gao,Multi-level Decision Making,Models, Methods and Application,Springer,Berlin,2015.

Qinghua Zhangreceived the BS degree from the Sichuan University,Chengdu,China,in 1998,MS degree from Chongqing University of Posts and Telecommunications,Chongqing,China,in 2003,and the PhD degree from the Southwest Jiaotong University,Chengdu,China,in 2010.He was at San Jose State University,USA,as a visiting scholar in 2015. Since 1998,he has been at the Chongqing University of Posts and Telecommunications,where he is currently a professor,and the associate dean of the School of Science.His research interests include rough set,fuzzy set,granular computing and uncertain information processing.

Guoyin Wangreceived the BS,MS,and PhD degrees from Xian Jiaotong University,Xian,China,in 1992, 1994,and 1996,respectively.He was atthe University of North Texas,and the University of Regina,Canada, as a visiting scholar during 1998-1999.Since 1996, he has been at the Chongqing University of Posts and Telecommunications,where he is currently a professor,the director of the Chongqing Key Laboratory of Computational Intelligence,and the dean of the College of Computer Science and Technology.He was appointed as the director of the Institute of Electronic Information Technology,Chongqing Institute of Green and Intelligent Technology,CAS,China,in 2011.He is the author of over 10 books,the editor of dozens of proceedings of internationaland nationalconferences,and has more than 200 reviewed research publications.His research interests include rough set,granular computing,knowledge technology,data mining,neural network, and cognitive computing.He is a senior member of the IEEE.

Qin Xiereceived the BS degree from Chongqing University of Posts and Telecommunications, Chongqing,China,in 2016.She is currently pursuing the MS degree in Chongqing University of Posts and Telecommunications,Chongqing,China.Herresearch interests include analysis and processing of uncertain data,Three-way decisions,and rough sets.

Available online 11 November 2016

*Corresponding author.

E-mail address:wanggy@cqupt.edu.cn(G.Wang).

Peer review under responsibility of Chongqing University of Technology.

http://dx.doi.org/10.1016/j.trit.2016.11.001

2468-2322/Copyright©2016,Chongqing University of Technology.Production and hosting by Elsevier B.V.This is an open access article under the CC BY-NCND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

Copyright©2016,Chongqing University of Technology.Production and hosting by Elsevier B.V.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).