基于测试信号法的HVDC附加次同步阻尼控制器设计

王　杉，张　超，王立德，王渝红，李兴源（. 四川大学电气信息学院，成都 60065；. 湖南省电力公司检修公司，长沙40004）



基于测试信号法的HVDC附加次同步阻尼控制器设计

王杉1，张超2，王立德2，王渝红1，李兴源1
（1. 四川大学电气信息学院，成都 610065；2. 湖南省电力公司检修公司，长沙410004）

[摘要]针对汽轮发电机组的次同步振荡（SSO）问题，从系统电气阻尼角度阐述了附加次同步阻尼控制器（SSDC）抑制次同步振荡的机理，进而提出一种基于测试信号法相位补偿原理的SSDC设计方法。对SSDC的结构、输入信号的选取、相位补偿等方面进行了论述和设计。在PSCAD/EMTDC中构建SSO的测试系统，基于测试信号法计算，该系统电气阻尼系数为负，表明测试系统会引发SSO。采用所设计的SSDC控制后，电气阻尼系数均为正。时域仿真也验证了所设计的SSDC能够有效抑制直流控制引起的SSO。

[关键词]测试信号法；次同步振荡；附加次同步阻尼控制器；电气阻尼系数；相位补偿

0　引言

HVDC输电快速可控，存在着与汽轮发电机组轴系发生次同步扭振相互作用的可能性[1]。随着大区域交直流混合输电大电网的形成，高压直流输电引起的次同步振荡问题越来越突出。确保电力系统安全稳定运行日益重要，因此研究抑制直流控制引起SSO的措施具有重要现实意义。

分析SSO问题的方法主要有频域扫描法，特征值法，时域仿真法和复转矩系数法。复转矩系数法由I.M. Canay提出，在分析交直流系统SSO问题时可以考虑换流器的非线性[2]。文献[3]提出基于广域测量系统的次同步振荡在线监测预警方法。文献[4]提出Prony算法的次同步扭振模态参数辨识。文献[5]提出基于TLS-ESPRIT算法设计SSDC，具有很强的鲁棒性。本文提出一种基于测试信号法相位补偿原理的SSDC设计方法来抑制直流控制引起的SSO。

1　测试信号法原理

测试信号法采用时域仿真的方法实现复转矩系数法。扰动施加在整流侧电流参考环节上，直流闭环控制能直接对扰动作出快速响应。对于一台待研发电机组，发电机电磁转矩的增量可用式（1）来表示[2]：

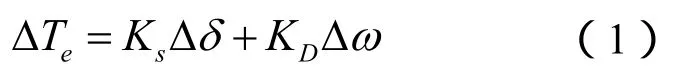
实现测试信号法具体步骤如下[6]：

（1）对确定的稳定运行点，整流侧定电流调节器的电流参考环节上施加小信号振荡电流△I0（包含不同的频率，频率范围为5Hz到45Hz），幅值为0.05p.u.。

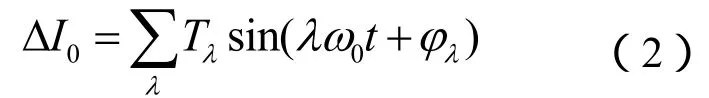
式中：λ<1，Tλ、φλ分别是小信号比例系数和初相位，要求Tλ较小。

（2）仿真到系统进入稳态，截取小值脉动一个公共周期上的发电机电磁转矩△Te和发电机角速度的变化量△ω。

（4）根据式（3），求出电气阻尼系数De：

文献[7]提出系统发生次同步振荡的判据为总阻尼D小于0，如式（4）所示。

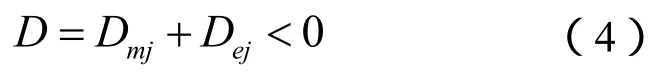
式中，Dmj为机组第j扭振模式的机械阻尼系数；Dej为机组第j扭振模式的电气阻尼系数。

2　SSDC的设计

2.1SSDC的设计原理

同时我们又单独测试了石英基底的荧光光谱，结果表明石英基底并不具有上转换荧光现象，由此可以证明上转换荧光是由基底表面的Ce3+掺杂YAG荧光薄膜材料所产生的。

根据测试信号法，系统的电气阻尼系数De可以用式（3）求得。SSDC提供的附加电磁转矩T△e′作用大小可用图1说明。

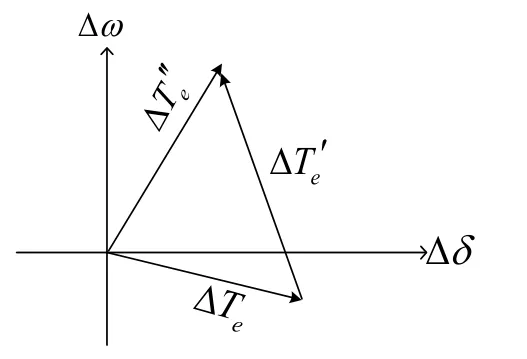
图1　电磁转矩变化量与转速偏差相位图

SSDC的设计原理是根据测试信号法原理，提供一个位于第1象限的具有超前相位的附加电磁转矩△Te′，使得△Te与△Te′的相量之和△Te″在第1象限，从而能够抑制SSO。

2.2SSDC的结构

基于2.1节的SSDC设计原理，从工程实践考虑，附加次同步阻尼控制器的结构如图2虚线框所示。SSDC由测量环节、PLL环节、带通滤波环节、相位补偿环节、增益环节及限幅环节构成。

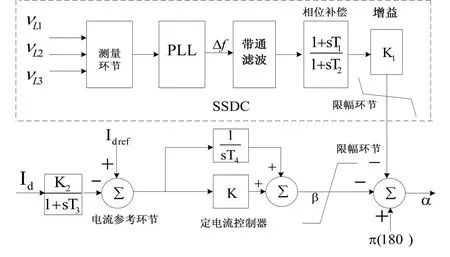
图2　SSDC结构和定电流控制框图

2.3.1输入信号的选择

SSDC采用的输入信号主要有发电机转速偏差△ω和系统频率偏差△f两种。△ω对次同步分量的响应特性较好，但实际工程中HVDC的换流站往往与发电厂有一定的距离。因此，SSDC采用就地频率偏差控制的方法更符合工程实际，通常采用整流侧换流母线电压信号作为测量环节的输入信号。

2.3.2相位补偿环节

相位补偿环节是SSDC设计的关键，参数选择不合适不但不能抑制振荡反而会加剧振荡。

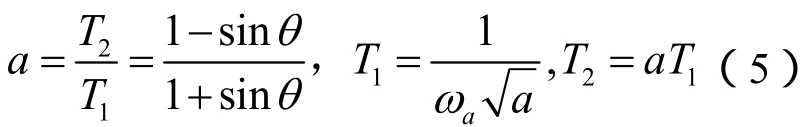
式中，ωa为所选择相位补偿的频率；θ为ωa所对应的需要补偿的超前相角；T1、T2为补偿环节的时间常数。

SSDC能够提供的附加电磁转矩的大小，不但与输入信号△f有关，还与图2中增益K1有关。因此，应根据系统实际的情况确定合理的K1值。

3　仿真分析

3.1测试系统

仿真分析采用的系统模型如图3所示。采用IEEE第一标准测试系统发电机模型G[8]，经变压器T1和换流变压器T2与直流系统连接。送端交流等值系统为SR，ZSR为其等效阻抗。受端系统为S1，ZS1为其等效阻抗，系统短路比为2.5。发电机额定容量为892.4MVA。

直流系统采用CIGRE直流输电标准测试系统[9]，直流额定输送功率为1000MW，额定电压为500 kV。直流系统采用单极12脉动结构，直流线路采用T型模型，整流侧采用定电流控制，逆变侧采用定熄弧角控制。定电流控制器的详细框图如图2所示，定电流控制器输出触发角信号α，其中K=1.0989，T4=0.01092 s；K2=0.5、T3= 0.0012 s。T1两侧电压为26 kV/345 kV，u%=0.14 p.u.，系统基准容量100 MVA，基准电压345kV。

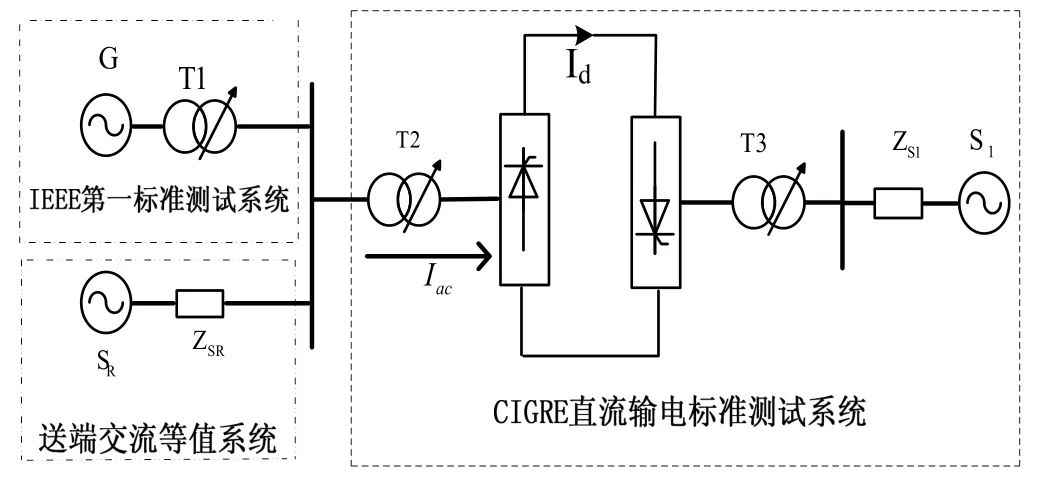
图3　仿真系统模型

3.2待补偿相位及SSDC参数设计

3.2.1待补偿相位

相位补偿环节是SSDC的关键环节。由前述分析可知，待补偿的相位是发电机组电磁转矩△Te到发电机组转速△ω的滞后相位。按第1节测试信号法的步骤，分析结果如图4所示。

图4　△Te与△ω的相频特性

△Te与△ω的相位差决定了系统电气阻尼系数的性质。根据图4可知，在23Hz以下低频段，△Te与△ω的相位差超过了90°；系统的电气阻尼系数De为负，则存在SSO的可能。

3.2.2SSDC参数设计

整流侧定电流控制器输出加入SSDC，如图3所示。控制器参数如下：PLL参数中KPLL_P=50，KPLL_INT=900；2阶带通滤波器带宽设置为5到45Hz。根据图4待补偿相位，为达到理想补偿相位设计2个一阶环节，在5Hz和15Hz分别补偿30°，相位补偿环节参数根据式（5）确定，2组参数中T1/T2分别为0.0559/0.00186和0.0275/0.0092；增益系数K1取值20，限幅环节范围为±0.05p.u.。

3.3阻尼特性分析

对于图3所示的仿真系统，根据测试信号法步骤，计算出无SSDC控制和加入SSDC的电气阻尼系数De。发电机组次同步频率范围内（5Hz到45Hz）的电气阻尼系数De的计算结果如图5。

图5　系统电气阻尼系数De仿真结果

基于测试信号法计算，由图5（a）可以看出，未加入SSDC时，系统30Hz以下电气阻尼均为负值，表明测试系统会引发SSO。由图5（b）可以看出，加入SSDC后系统电气阻尼均为正值，表明SSDC能够为系统提供正阻尼来抑制SSO。

3.4时域仿真结果

为了验证SSDC参数的有效性，利用PSCAD/EMTDC程序对图3所示的系统进行时域仿真。发电机轴系由高压缸HP、中压缸IP、低压缸LP以及发电机GEN和励磁机EXC 5个集中质量块组成。参数同IEEE第一标准测试系统模型，其中30Hz以下振荡模式的频率依次为15.71Hz、20.21Hz和25.55Hz。对应的机械阻尼系数Dmj分别为0.54、12.2和0.775。由图5所示的电气阻尼特性可知，无SSDC时15.71Hz对应的电气阻尼系数为-1，根据式（4）计算，轴系的总阻尼系数为-0.46，因此轴系发生该振荡模式的扭振。

SSDC采用3.2.2节的控制参数，2s时刻在电流参考环节施加小信号振荡电流△I0，扰动持续5个工频周期（0.1 s）。通过时域仿真分析无SSDC及加入SSDC两种情况下系统发生扰动时发电机各段轴系转矩变化，如图6所示。

由图6（a）可以看出，未加入SSDC控制时，系统受扰动后发电机各段轴系的转矩都是发散的，表明SSO模式不稳定。由图6（b）可以看出，加入SSDC后发电机各段轴系上的转矩迅速衰减，说明SSDC有效抑制了轴系的扭振振荡，这与电气阻尼特性分析的结果一致，表明SSDC能有效抑制由于直流系统控制所引起的SSO。

图6　系统发生扰动是发电机各段轴系转矩仿真结果

4　结语

（1）论述了测试信号法计算系统电气阻尼系数的原理。从电气阻尼特性角度阐述SSDC抑制SSO的机理，进而提出基于测试信号法相位补偿原理的SSDC设计方法。

（2）重点阐述了SSDC设计中的控制器结构、输入信号的选取、相位补偿等方面，提出了一种便于工程实现的SSDC设计方案。

（3）在PSCAD/EMTDC中构建了次同步振荡的测试系统。采用文中所设计的SSDC参数，测试系统在加入SSDC后，系统电气阻尼系数由负阻尼调整为正阻尼。时域仿真结果也验证了所设计的SSDC能够有效抑制直流控制引起的SSO。

[参 考 文 献]

[1] 徐衍会. 复杂多机系统次同步振荡的分析与抑制[J]. 电力系统保护与控制, 2011, 39(11): 83-88.

[2] 刘超, 蒋东翔, 谢小荣, 等. 次同步振荡引起的发电机组轴系疲劳损伤[J]. 电力系统自动化, 2010, 34(15): 19-22.

[3] 王茂海, 高洵, 王蓓, 等. 基于广域测量系统的次同步振荡在线监测预警方法[J]. 电力系统自动化, 2011, 35(6): 98-102.

[4] 胡允东, 王西田, 刘石. 基于EMD和Prony算法的次同步扭振模态参数辨识[J]. 华东电力, 2012, 40(5): 0788-0792.

[5] 蒋平, 吴熙, 罗曦. 基于TLS-ESPRIT算法的附加励磁阻尼控制抑制次同步振荡[J]. 电力自动化设备, 2009, 29(10): 25-29.

[6] 张帆, 徐政. 直流输电次同步阻尼控制器的设计[J]. 电网技术, 2008, 32(11): 13-18．

[7] 倪以信, 王艳春, 陈寿孙, 等. 多机系统直流输电引起的次同步振荡的研究[J]. 中国电机工程学报, 1993, 13(2) : 64-71.

[8] IEEE Subsynchronous Resonance Task Force. First Benchmark Model for Computer Simulation of Subsynchronous Resonance. IEEE Trans on PAS, 1977, PAS-96(5): 1565-1572.

[9] 徐政. 交直流电力系统动态行为分析[M]. 北京:机械工业出版社, 2005: 44-47.

王杉(1988-)，主要研究方向：电力系统稳定与控制，高压直流输电，新能源并网，硕士研究生。

审稿人：李桂芬

Design of HVDC Supplementary Subsynchronous Damping Controller Based on Test Signal Method

WANG Shan1, ZHANG Chao2,WANG Lide2, WANG Yuhong1, LI Xingyuan1
(1. School of Electrical Engineering and Information, Sichuan University, Chengdu 610065, China; 2. Maintenance Branch of Sichuan Electric Power Company, Deyang 618500, China)

Abstract:Aiming at subsynchronous oscillation (SSO) problem of turbine-generator unit, the mechanism of inhibiting SSO with supplementary subsynchronous damping controller (SSDC) was described from the view of an electrical damping characteristics in system. Based on the phase compensation principle, a method to design SSDC according to test signal method was proposed. Structure of SSDC, selection of input signal, phase compensation, etc are discussed and designed. The test system was constructed in PSCAD/EMTDC program. System electrical damping coefficient is negative, which shows that can lead to SSO. Then the electrical damping of system with SSDC are positive. Time domain simulation results validate the effectiveness of the designed SSDC.

Key words:test signal method; SSO; SSDC; electrical damping coefficient; phase compensation

[作者简介]

[收稿日期]2015-05-14

基金项目:国家高技术研究发展计划（863计划）项目（2011AA05A119）；国网四川省电力公司检修公司科技项目（SGSCJXOOYJKJ1301058）。

[中图分类号]TM714

[文献标识码]A

[文章编号]1000-3983(2016)01-0006-04