内置扭带管Cu-水纳米流体的流动和传热特性

孙　斌，颜鼎峰，杨　迪

(东北电力大学 能源与动力工程学院，吉林 吉林 132012)



内置扭带管Cu-水纳米流体的流动和传热特性

孙斌，颜鼎峰，杨迪

(东北电力大学 能源与动力工程学院，吉林 吉林 132012)

摘要：为了研究纳米流体在内置扭带管表面传热特性及流动特性，设计并建立一套纳米流体表面传热实验系统，Reynolds数(Re)在2 000-7 000的范围内，分别对质量分数为0.1%，0.3%和0.5%的Cu-水纳米流体在不同扭转比的内置扭带管中的传热特性进行实验研究。结果表明：随着Re增加，Cu-水纳米流体和去离子水的沿程阻力系数均减少；水的沿程阻力系数小于Cu-水纳米流体，内置扭带管的沿程阻力大于光管，且随着扭转比的增大而减少；Nusselt数(Nu)随Re和纳米颗粒质量分数的增大而增大；Cu-水纳米流体的Nu比水高，质量分数为0.5%的Cu-水纳米流体在Y=3.5与Y=5.5的内置扭带管的增强幅度分别为2.29与2.14；内置扭带管的Nu比光管大，且随扭转比增大而减少。

关键词：纳米粒子；传热；流动；内置扭带管

20世纪90年代以来，研究人员开始探索将纳米材料技术应用于强化传热领域，研究新一代高效传热冷却技术。1995年，美国Argonne国家实验室的Choi[1]等人首次提出了一个崭新的概念——“纳米流体”。近些年来，国内外学者对纳米流体技术进行了大量的研究，主要集中在以下几个方面[2-5]：纳米流体体系的选择、纳米流体的制备及稳定性研究、纳米流体热导率影响因素及模型研究、纳米流体强化传热机理研究、纳米流体粘度测量及影响因素研究。纳米流体是在基液中添加金属、非金属或聚合物固体粒子。基液中加入导热系数较大的固体粒子，使其导热系数比基液提高很多，所以，纳米流体在强化传热领域有广泛的应用前景。1873年，Maxwell[6]首次从理论上计算了悬浮液的有效导热系数。1993年，日本Tohoku大学的Masuda等[7]在水中分别添加平均粒径为13 nm的γ-Al2O3和平均粒径为2 7nm的TiO2粒子，制备了不同体积浓度的悬浮液，应用瞬态热线法测试了纳米粒子悬浮液的导热系数，试验结果表明，在液体中添加纳米粒子，显著增加了液体的导热系数。吕伦春等[8]在稳定的低压条件下，对以水-Cu纳米流体为工质的小型平板式毛细泵回路(CPL)的换热特性进行了实验研究，实验证明了水-Cu纳米流体是一种适合在CPL中使用的强化传热工质。王鹏[9]等采用Eulerian-Eulerian模型和Eulerian-Lagrange模型研究了TiO2-水纳米流体在水平管内的湍流流动特性，发现纳米流体流动特性的改变是影响其强化换热的主要因素。管内插入扭转带是一项强化传热的节能技术[10]，它具有制造工艺简单，成本低廉，等优点。管内插入扭带能使流体发生旋转运动，增加了旋转流体的流动路径，增加了贴近壁面流体的流动速度，加强了边界层流体的扰动以及边界层流体和主流流体的混合，从而加强了传热效果。对于扭带管，众多学者进行了较细致而全面的研究，文献[11]从管径、扭带扭曲率、工质普朗特数等不同方面对扭带管性能的影响做了详细的概述。

目前，关于纳米流体稳定性、流动特性、传热特性方面已有很多学者进行了研究[12]，但纳米流体表面传热特性方面还需深入研究，而有关扭带强化传热的研究国内外都有过综合性的报道，其中介绍了一些传热和流动阻力特性的综合关系式，但这些综合关系式是在较高的Reynolds数范围或是在较低Reynolds数范围获得的，应用条件有很明显的局限性。针对这一现状，本文自行设计并建立了一套纳米流体在内置扭带管的表面传热实验系统，在Reynolds数2 000-7 000的范围内，对不同质量分数Cu-水纳米流体，在不同扭转比的内置扭带铜管与光管的对流换热特性进行对比实验研究，以期掌握一些基本传热规律，为纳米流体的实际应用提供技术支持。

1实验设计与数据处理

1.1纳米流体的制备

目前，对于纳米流体的制备有两种方法：“一步法”与“两步法”。两种方法相比较，“一步法”造价昂贵，于是本文采用“两步法”，即取一定量的纳米颗粒和分散剂，加入到去离子水中，进行搅拌，然后用超声波振荡仪进行振荡，得到悬浮的Cu-水纳米流体。

本文所选用的Cu纳米颗粒，平均粒径为50 nm纯度99%，选用的分散剂为十二烷基苯磺酸钠(SDBS)。

1.2纳米流体的稳定性分析

通过选取不同质量分数的分散剂，使用岛津UV-2550紫外可见分光光度计，测量不同质量分数的纳米流体的透射比，从而研究其稳定性，选取最佳质量分数的分散剂，实验结果如图1及图2所示，图1中，纵坐标为透射比，横坐标为分散剂的质量分数，当透射比越小时，稳定性越好，由图可以看出纳米流体的质量分数与分散剂质量分数为1∶1时，稳定性最好；图2为Cu-水纳米流体与SDBS为1∶1时，时间对稳定性的影响，由图可以看出随着存放的时间增加，稳定性变差。

图1 不同质量分数分散剂对稳定性的影响图2 时间对稳定性的影响

1.3实验设计

该实验系统主要包括纳米流体储存部分、测试部分、冷却部分、预热部分和数据采集部分，如图3所示。测试部分为系统的核心，测试部分由加热水箱及不同扭转比的内置扭带管组成。扭转带是用宽度与内管内径相等的铜带沿长度轴向扭曲而成，通常把扭转180°的轴向长度H称为扭转带的节距，并把H与管内径D之比称为扭转比Y=H/D，其结构如图4所示，本实验采用厚度δ=1 mm，宽度D=8 mm，扭转比Y=3.5、4.5、5.5的扭转带，扭转带的尺寸如表1所示。加热水箱提供了热量，水箱尺寸为1000×300×300 mm，在水箱外壁包裹硅酸铝绝缘材料及铝箔胶带提供稳定性和绝缘性。预热部分用于消除入口效应，并增加实验数据的准确性，预热部分长度1 m，由换热管及外壁螺旋缠绕的镍铬合金电阻丝组成，电阻丝直径为1.2 mm，在电阻丝外包裹硅酸铝绝缘材料及铝箔胶带。冷却部分由一弯曲的线圈和一个恒温水箱，以确保工作流体被恢复到初始温度。本实验系统共安装6组Pt100热电阻，其中一组安装在预热段，用于测量预热段入口温度；两组安装在测试部分的入口及出口，用于测量试验段的入口及出口温度；其余的热电阻均匀安装在管壁，用于测量试验段管壁温度。试验段进出口压差由Rosemount 3051S电容式差压变送器测量。进出口压力由WP401A-5G24E2N压力变送器测量。纳米流体由磁循环泵用来提供动力，使纳米流体可以通过流量变送器进入实验系统。该磁循环泵的输入功率为125 W，扬程为30 m。实验中流体的流量通过阀门调节，热量通过改变加热电压调节。每次测试之后，均对整个测试系统反复清洗，以防止残余纳米流体对测试结果的影响。

1-实验段；2-加热水箱；3-热电阻；4-压差计；5-预热部分；6-压力计；7-数据采集系统；8-计算机；9-截止阀；10-储液槽；11-涡轮流量变送器；12-磁力驱动泵；13-水冷器图3　实验系统

图4　扭转带结构示意图

TwistratioY=H/DWidthH,mDiameterD,m3.50.0280.0084.50.0360.0085.50.0440.008

1.4数据处理

由牛顿冷却定律

Q=hA(Tw-Tavg)，

(1)

其中，

A=πDL，

(2)

Tavg=(Tout+Tin)/2，

(3)

(4)

热水箱提供的热流量

Q=I2R ，

(5)

(6)

由能量方程得到沿程阻力系数为

f=2ΔPD/lρu2，

(7)

(8)

(9)

由于纳米粒子的体积难以精确测定，纳米流体中的粒子体积份额可以由粒子的质量百分比计算，由下式表示：

(10)

由于纳米流体中纳米颗粒的体积分数小于5%，故纳米流体的粘度采用Einstein公式[13]计算：

μnf=(1+2.5φ)μbf，

(11)

v=μnf/ρ .

(12)

纳米流体的密度ρ按式(13)[14]计算：

(13)

纳米流体的比热容由式(14)[15]计算：

Cp=ΣC1·φ1.

(14)

1.5不确定度评估

为了得到更准确的实验结果，需要对系统进行误差分析及不确定度评估[16]，使用仪器的参数及不确定度见表2，变量的不确定度见表3。

表2　仪器的参数及不确定度

表3　实验中变量的不确定度

2实验结果与讨论

2.1理论验证

在管内中插入扭带，流体按照螺旋运动的规律流动，文献[17]给出的旋转流体的传热关联式为

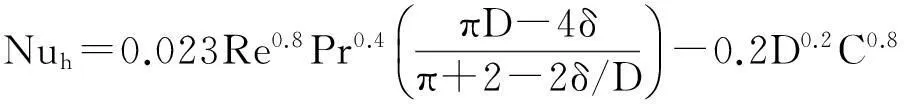
(15)

其中,

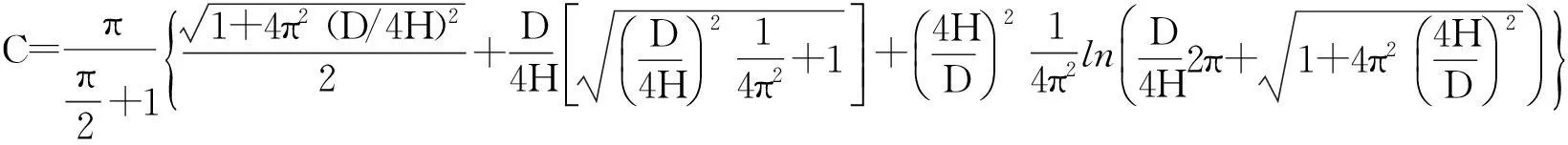
(16)

在实验开始前需对实验系统可靠性进行检验，将去离子水在扭转比Y=3.5的内置扭带管的实验数据与式(14)的计算结果进行比较，结果如图5所示，由图中可知平均误差为4.07%，能够满足实验要求。

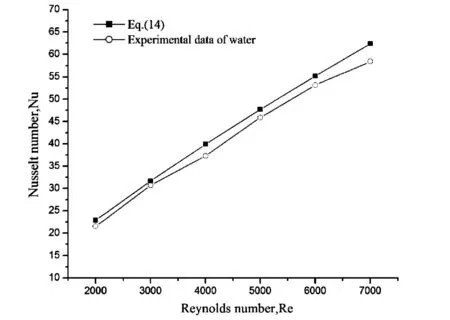
图5　实验数据与式(14)比较

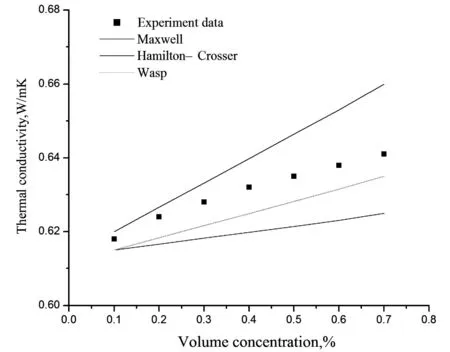
图6　不同模型热导率的比较

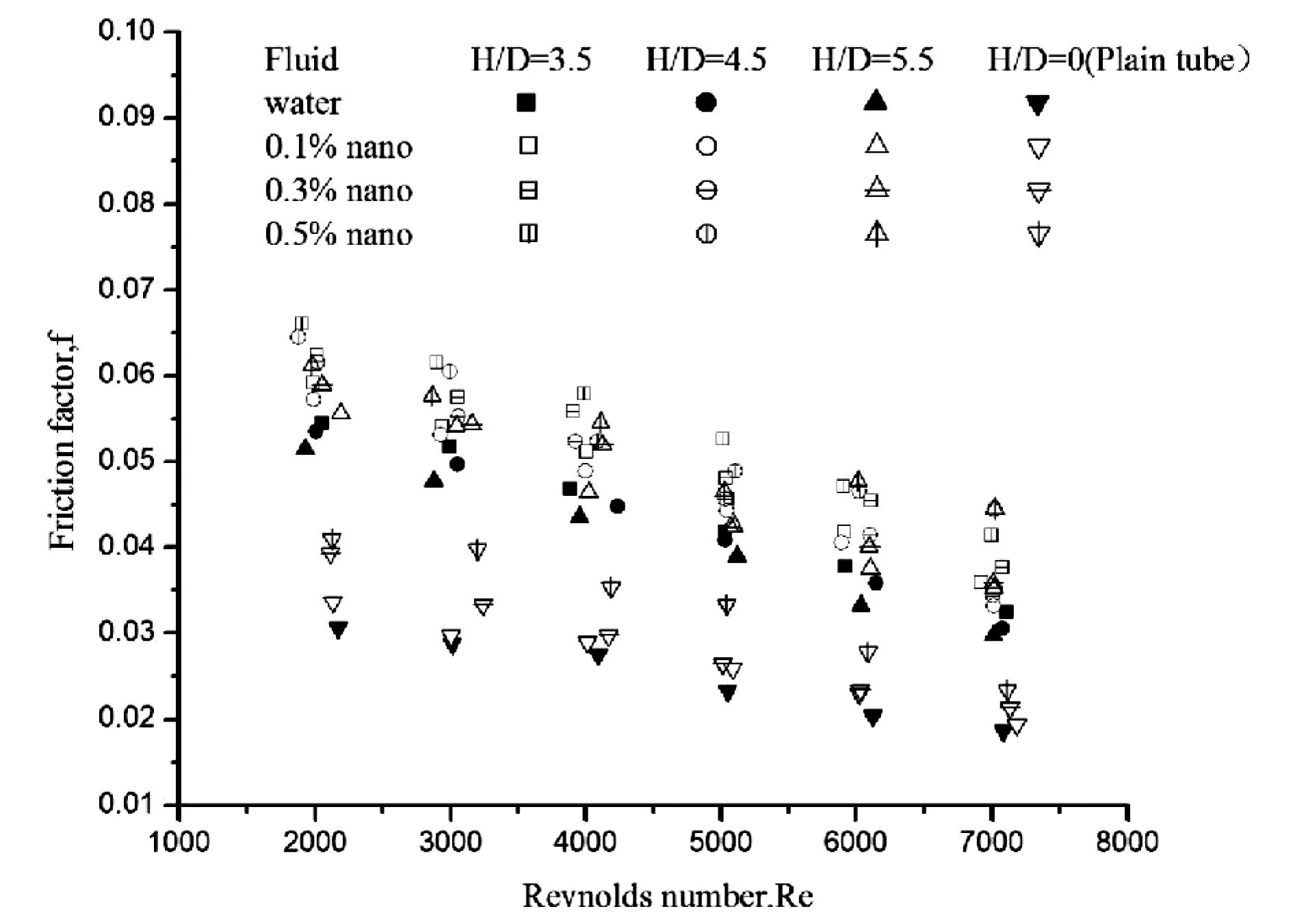
图7　Cu-水纳米流体在不同管中的沿程阻力系数f

2.2纳米流体的热导率

采用瞬态热线法[18]测量纳米流体的热导率，距离线源r处的液体温升ΔT (r，t)[19]为

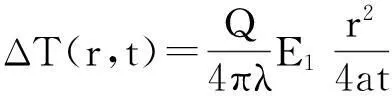
(17)

式中：Q为热流量;W，λ为热导率，W·m-1·K-1；t为时间；s，E1(x)为指数积分。

将式(17)两边微分，得到

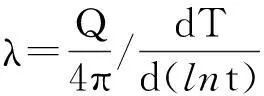
(18)

常用的流体热导率模型有以下几种：

(1)Maxwell模型[20]

(19)

(2)Hamilton-Crosser模型[21]

(20)

(3)Wasp模型[22]

(21)

热导率测量结果与几种模型计算结果的对比如图6所示。由图中可以看出，Maxwell模型的误差最大，其次是Hamilton-Crosser模型，Wasp模型的误差最小。

2.3流动特性

实验中通过调节阀门改变流量，得到不同雷诺数下，去离子水、0.1%、0.3%和0.5%的Cu-水纳米流体在不同扭转比的内置扭带管及光管的进出口压力差，根据式(7)计算得到的沿程阻力系数f如图7所示。由图7可以看出， f随着Re增大而减少；相同Re下，在相同Y的内置扭带管中水的f小于Cu-水纳米流体，沿程阻力系数f随着φ的增大而增加。相同Re下，内置扭带管的f大于光管，这是由于管内插入扭带后，使流体发生螺旋流动增加了流动路径并且产生碰撞，从而增加了沿程阻力。f随着Y增加而减小，这是由于Y增大导致贴壁路径减小，从而使f减少。

2.4传热特性

通过实验研究了去离子水和质量分数为0.1%、0.3%和0.5%的Cu-水纳米流体的传热特性，得到图8所示的结果。由图8中可以看出，Nu随着Re增大而增加；在相同Re下，Cu-水纳米流体的Nu比去离子水有较为显著地提升，主要原因是纳米颗粒的加入提高了流体与内置扭转带和管壁的碰撞和热传递，在近壁区提高了流体的有效旋流，从而提高对流换热；内置扭带管的Nu比光管大，证明了内置扭带换热管有强化传热的作用；0.5%的Cu-水纳米流体的Nu最大，即随着φ的增大而增加。这是由于随着φ的增大，液体与颗粒、颗粒与颗粒、颗粒与管壁间的碰撞加强，从而强化了传热效果；由图9中可以看出，在相同Re下，Nu随Y的增大而减小。这是由于Y越小，贴近壁面的流体速度越大，从而加强了边界层流体的扰动以及边界层流体和主流流体的混合，使传热得以强化。

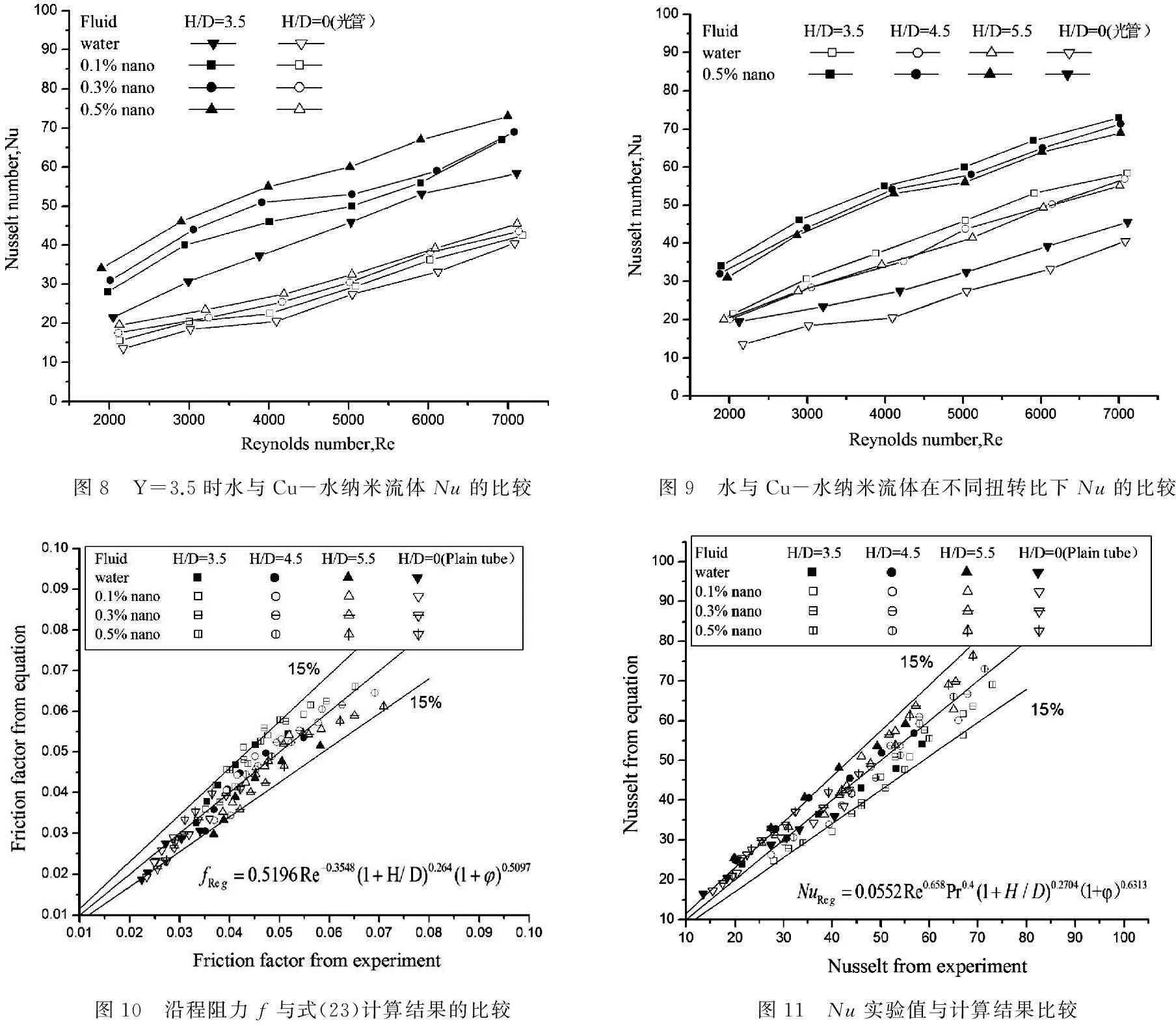
图8 Y=3.5时水与Cu-水纳米流体Nu的比较图9 水与Cu-水纳米流体在不同扭转比下Nu的比较图10 沿程阻力f与式(23)计算结果的比较图11 Nu实验值与计算结果比较

2.5增强幅度

纳米流体的传热强化幅度Nunf/Nuw，Nunf为不同φ的纳米流体在内置扭带管的Nu，Nuw为工质为水在光管的Nu。由文献[23]可知，内置扭带管的强化机理主要由当量直径减小效应，螺旋线流动流速加大效应及二次流流速加大效应组成，得到强化幅度的计算关联式(22)，计算得到不同质量分数纳米流体的平均强化幅度见表4。

表4　内置扭带管的增强幅度

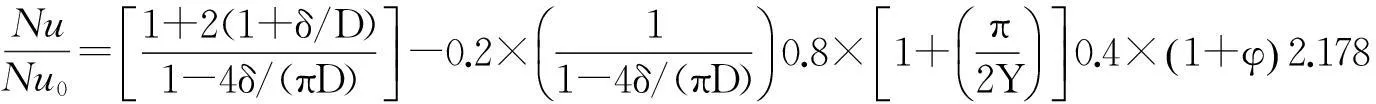
(22)

2.6验证回归方程

利用matlab拟合得到沿程阻力f及Nu的关联式为

fReg=0.519 6Re-0.354 8(1+H/D)0.264(1+φ)0.509 7 ，

(23)

NuReg=0.055 2Re0.658Pr0.4(1+H/D)0.270 41+φ0.631 3，

(24)

式中：0<φ<0.5，3.5

图10为沿程阻力f的实验值与式(23)计算结果的比较，由图可知计算结果与实验数据吻合良好，其平均偏差为7.48%，标准偏差为5.7%，最大偏差为23.9%。

图11为实验数据所得Nu与式(24)计算结果的比较。由图中可知，计算结果与实验数据吻合较好，Nu的平均偏差为8.91%，标准偏差为6.21%，最大偏差为27.13%。

3结论

(1)Cu-水纳米流体的沿程阻力系数f随着Re增大而减小，随质量分数增大而增大；相同Re下，内置扭带管的沿程阻力系数f大于光管，且随扭转比Y的增加而减少。

(2)Cu-水纳米流体的Nu随Re和纳米颗粒质量分数φ的增大而增大。φ=0.5%的Cu-水纳米流体在Y=3.5与Y=5.5的内置扭带管的增强幅度分别为2.29与2.14。相同Re下，内置扭带管的Nu比光管大，且随扭转比Y的增大而减小。

(3)基于实验数据，拟合了Cu-水纳米流体在内置扭带管中的流动及传热关联式。

参考文献

[1]S.U.S.Choi，Enhancing thermal conductivity of fluids with nanoparticles[J].ASME FED，1995，231(66):99-105.

[2]孙斌，刘彤.纳米流体在内置扭带管的传热数值模拟[J].东北电力大学学报，2015，35(2)：10-17.

[3]Y.M.Xuan，Q.Li.Investigation on convective heat transfer and flow features of nanofluids[J].Heat Trans，2003，125(1):151-155.

[4]Lee，S.，Choi，S.U.S.，Li，S.and Eastman，J.A..Measuring thermal conductivity of fluids containing oxide nanoparticles[J].Journal of Heat Transfer，1999，121(2):280-289.

[5]张邵波，骆仲泱，寿春晖，倪明江，岑可法.层流区CuO-水纳米流体流动与对流换热特性[J].中国电机工程学报，2009，29(32)：58-59.

[6]Maxwell J C.A Treatise on electricity and magnetism[M].2nd ed.London:Clarendon Press.1881.

[7]Masuda，H.，Ebata，A.，Teramae，K..Alternation of thermal conductivity and viscosity of liquid by dispersing ultra-fine particles (dispersion of γ-Al2O3，SiO2and TiO2ultra-fine particles)[J].Netsu Bussei (Japan)，1993，4:227-233.

[8]L Lunchun，LIU Zhenhua.Thermal performance of small capillary pumped loop using water-Cu nanofluids[J].CIESC Journal，2008，59(11):2713-2717.

[9]WANG Peng，BAI Minli，Lv Zuji，HU Chengzhi，WANG Yuyan.Turbulent flow characteristics of nanofluids inside circular tube[J].CIESC Journal，2014，65(S1):17-26.

[10] 董承康，陶正文等.扭转带强化传热:实验研究和应用评价[J].工程热物理学报，2002，23(S):77-78.

[11] S.W.Chang，T.L.Yang，J.S.Liou.Heat transfer and pressure drop in tube with broken twisted tape insert[J].Exp Therm and Fluid Sci，2007，32(2):489-501

[12] 张海佳，李惟毅，云海涛.TiO2-蒸馏水纳米流体在内螺纹铜管内表面传热试验研究[J].机械工程学报，2012，48(12):151-152.

[13] C.T.Nguyen，F.Desgranges，N.Galanis，G.Roy，T.Maré，S.Boucher，H.A.Mintsa，Viscosity data for Al2O3-water nanofluid—hysteresis:is heat transfer enhancement using nanofluids reliable[J].Therm Sci，2008，47(2):103-111.

[14] L.S.Sundar，M.T.Naik，K.V.Sharma，M.K.Singh，T.C.S.Reddy，Experimental investigation of forced convection heat transfer and friction factor in a tube with Fe3O4magnetic nanofluid[J].Experimental Thermal and Fluid Science，2012，37(2):65-71.

[15] 彭小飞，俞小莉.低浓度纳米流体比热容实验研究[J].材料科学与工程学报，2007，25(5):719-722.

[16] T.G.Beckwith，R.D.Marangoni，J.H.Lienhard，Mechanical Measurements[M].fifthed.，New York:Addison-Wesley Publishing company，1990:45-112.

[17] 苟峰.管内插入扭带强化传热的试验研究[D].北京:中国原子能科学研究院，2002.

[18] 李强，宣益民.纳米流体的热导率的测量[J].化工学报，2003，54(1):42-46.

[19] H.S.Carslaw，J.C.Jaeger，Conduction of Heat in Solids[M].2nd ed.，London:Oxford University Press，1959:510.

[20] J.C.Maxwell，A.Treatise on Electricity and Magnetism[M].Second ed.，UK:Oxford Clarendon press，1881:435

[21] R.L.Hamilton，O.K.Crosser，Thermal conductivity of heterogeneous two component systems[J].I&ECFundam，1962，1 (3):187-191.

[22] F.J.Wasp，Solid-liquid slurry pipeline transportation[J].Trans Tech，1977.

[23] 张琳，钱红卫，俞秀民，宣益民.内置旋转扭带换热管的传热强化机理[J].机械工程学报，2007，43(1):139-143.

[24] E.J.Wasp,J.P.Kenny,R.L.Gondhi.et,al.Solid-liquid flow:slurry pipeline transportation[J].Ser.bulk Mater.handl,1976,1:4.

Flow and Heat Transfer Characteristics of Cu-water Nanofluids in Twisted-Tape Inserts in Tubes

SUN Bin，YAN Ding-feng，YANG Di

(Energy Resource and Power Engineering College，Northeast Dianli University，Jilin Jilin 132012)

Abstract：In order to study the heat transfer characteristics of nanofluids in twisted-tape inserts in tubes，the heat transfer experimental system are designed and built，in the range of 2000～7000 of the Reynolds number，respectively for the nanofluids Cu-water in the mass fraction of 0.1%，0.3%，0.5% heat transfer characteristics of twisted-tape inserts in tubes.The results of experiments show that the friction factor decreased as the Reynolds number increased.The friction factor of the nanofluids was higher than the friction factor of water.The friction factor of twisted tape insert pipe was higher than the friction factor of plain tube，and the friction factor decreased as the twist ratio increased；The Nusselt number increased with the Reynolds number；The Nusselt number of the nanofluids increased with concentrations of nanoparticles；the Nusselt number of Cu-water nanofluids is higher than the Nusselt number of water.The enhancement with Cu-water nanofluid of 0.5% mass fraction for twist ratio of 3.5 and twist ratio of 5.5 is 2.29 and 2.14 respectively；the Nusselt number of twisted tape insert pipe was higher than the plain tube，and the Nusselt number decreased as the twist ratio increased.

Key words：Nanoparticles；Heat transfer；Flow；Twisted-tape inserts in tubes

中图分类号：TK124

文献标识码：A

文章编号：1005-2992(2016)01-0074-08

作者简介：孙斌(1972-)，男，吉林省永吉县人，东北电力大学能源与动力工程学院教授，博士，主要研究方向：多相流动理论及应用.

收稿日期：2015-12-10