一种协同定位算法在智能照明系统中的应用

傅军栋, 张　胤

(华东交通大学 电气与电子工程学院，南昌　330013)



一种协同定位算法在智能照明系统中的应用

傅军栋, 张胤

(华东交通大学 电气与电子工程学院，南昌330013)

摘要：灯具是智能照明系统的控制对象，而控制灯具的前提是找到灯具的位置；针对灯具的定位问题，提出了一种基于加权质心和泰勒级数展开的协同定位算法；为使定位更加稳定与精确，该算法利用加权质心算法对未知节点进行初始定位，再将其作为泰勒级数展开算法的初值，精确估计未知节点的位置；仿真结果表明，与传统的加权质心算法相比，该协同定位算法收敛性好，定位精度高，最大定位误差小于1.8 m，平均定位误差可以达到0.7 m；这种定位算法应用于智能照明控制系统中，有利于精确地对灯节点进行控制。

关键词：智能照明系统；节点定位；测距；加权质心；泰勒级数展开

0引言

在现有的多数智能照明控制中，需要预先定义好节点的编码，再安装时还需记录节点编码对应的位置信息，设置相对复杂。随着物联网的不断发展，ZigBee技术得到了广泛的推广和应用。采用ZigBee无线传感网络构建的智能照明系统[1]，在照明设备上安装ZigBee就可以将灯节点转换为对无线网络节点的控制，如果能够通过信号的强弱及方位来获取灯的物理位置，将有利于对灯进行可视化设置。本文主要以基于ZigBee的无线传感网构建的智能照明系统[2]为研究内容，实现智能照明系统中灯节点的快速定位。

多年来，对于无线传感网络节点的定位技术国内外专家学者提出了许多算法[3]。根据是否需要测量节点间的距离分为两类：一类是基于测距的定位算法(Range-Based)；另一类是无需测距的定位算法(Range-Free)，基于测距的节点定位算法，文献[4]提出了一种基于TOA的定位算法，该算法利用发出无线信号的节点到接收信号节点的时间计算两节点间的距离，对节点时间的同步性要求高，且耗能大。基于非测距的节点定位算法，文献[5]提出了一种Centroid定位算法，该算法仅利用节点间的网络连通度，将未知节点邻近的信标节点的质心作为未知节点的位置。文献[6]提出了一种DV-HOP定位算法，该算法首先计算网络平均每跳的距离，然后计算未知节点到信标节点的跳数，最后利用平均每跳的距离跟跳数来计算未知节点的位置。

对于无线智能照明系统来说，对灯节点的定位精度要求较高，然而上述的定位算法误差较大、定位精度不高，针对上述问题，本文提出了一种基于加权质心和泰勒级数展开相结合的协同定位算法。该算法首先利用RSSI测距模型计算节点间的距离，然后利用加权质心算法估计未知节点的大概位置，最后用泰勒级数展开精确的定位未知节点的位置。该算法定位精度较高，能够满足无线智能照明系统灯节点的定位要求。

1智能照明系统的组成

由ZigBee[7]无线信号通信的基本原理可知，整个照明系统主要由终端节点(灯节点)、协调器节点、上位机及Android手机组成。本系统的结构如图1所示。在整个ZigBee网络中，终端节点以路由的方式加入，同时具有终端节点采集和控制的功能。协调器在完成自组网的情况下广播发送查询未知节点(不知道具体坐标位置的节点)的命令，未知节点在收到查询命令后，向周围的信标节点(已知坐标位置的节点)发送8次blast信号，信标节点在收到未知节点的blast信号后，记录下与该未知节点的RSSI值，然后对这8个RSSI值取平均，最后所有信标节点通过ZigBee[8]网络把处理得到的RSSI平均值发送给协调器节点，协调器节点在通过串口将数据传给上位机，上位机经过协同定位算法处理后，求出未知节点的坐标。然后把未知节点的坐标显示在监控软件的界面上，以便用户对终端节点进行操作。同时上位机通过WiFi可以把未知节点的坐标发送到手机供手机显示，用户通过手机也可以对终端节点进行操作，开关或者对灯具进行调光等。

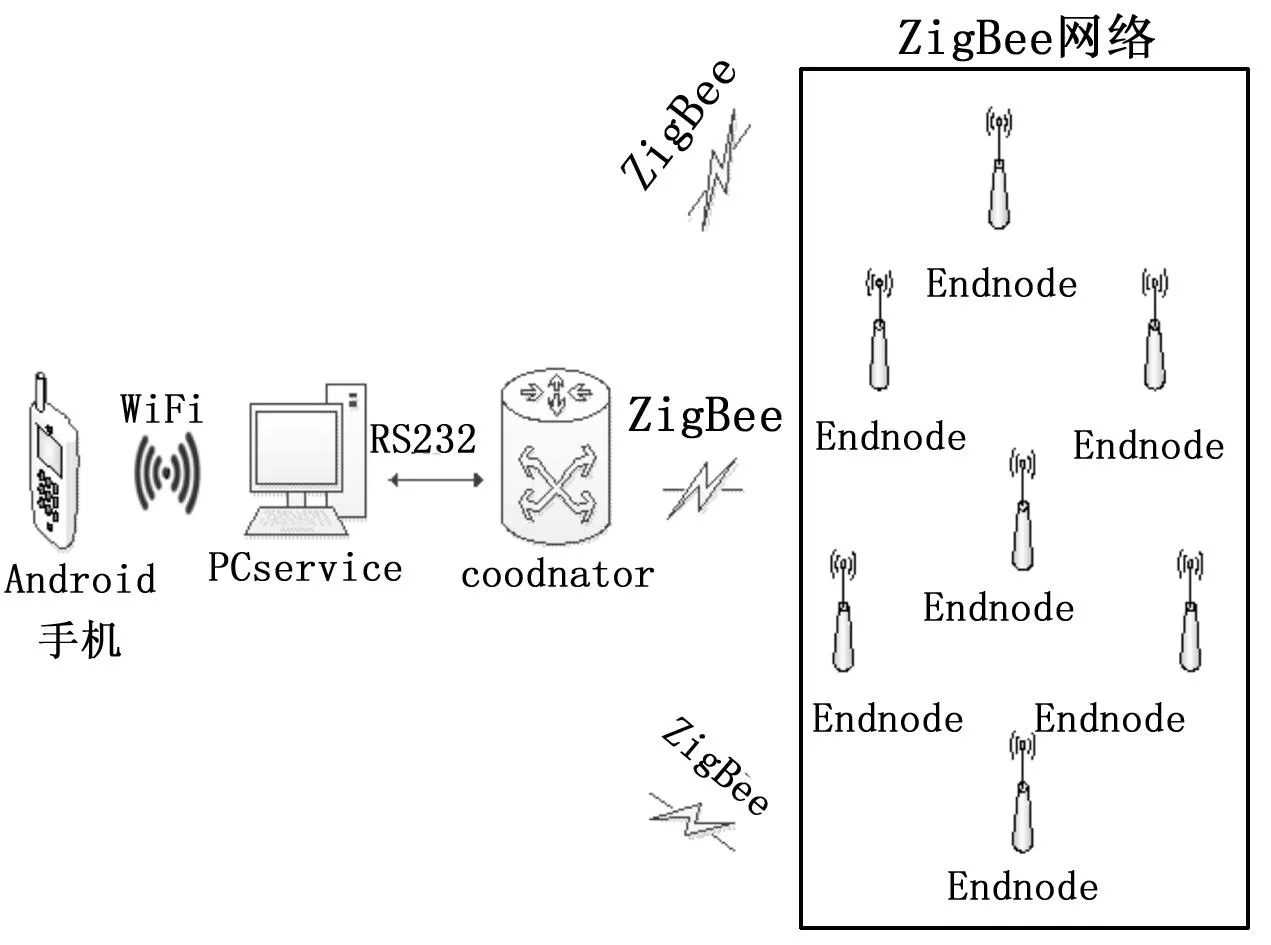
图1　智能照明系统结构图

2定位算法原理

2.1RSSI室内传播模型

由无线信号通信的基本原理可知，无线信号在传播的过程中，信号强度随传播距离的增加而有规律地衰减。因此，可以通过信号强度与距离的关系来求得节点间的距离。目前，比较常见的RSSI[9]—距离传播模型有自由空间传播、shadowing、两径放射、哈它等模型，室内环境由于存在多径反射、非视距、障碍物等的影响，一般采用更具综合性的Shadowing传播模型。Shadowing传播模型如式(1):

(1)

式(1)中，d表示接收端到信号源的距离，PL(d)表示相距为d时，接收端接收到的信号强度，单位为dBm，d0表示参考距离，一般取1 m，PL(d0)表示距离为1 m时的接收信号强度，n表示路径损耗系数，表示信号强度随距离增加时的衰减速率，ε是均值为0，均方差为σ(dB)的高斯白噪声，令PL(d0)=A，PL(d)=RSSI，则式(1)化简为：

(2)

在实际应用中，一般不考虑高斯白噪声，采用简化的Shadowing模型，如式(3)：

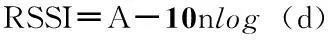
(3)

根据公式(3)求出距离的表达式：

(4)

在一些文献中给出了A和n的取值范围，如表1所示，本实验因为在办公室中进行，A取-50，n取2，利用公式(4)求得节点间的距离。此距离在代入加权质心算法中求得未知节点的初始坐标。

2.2加权质心算法

质心算法仅考虑网络连通度，首先设定一个通信半径，然后记录能与未知节点进行通信的信标节点的坐标。最后把这些信标节点组成的多边形的质心作为未知节点的坐标，显然，质心算法的定位精度不高，只能实现粗略的定位，而且非常依赖于信标节点的数量，但其计算简单，仅仅需要考虑网络的连通度。假设未知节点坐标为(X,Y,Z)，能与其进行通信的k个信标节点坐标为(x1,y1,z1)，(x2,y2,z2)，……(xk,yk,zk)，则未知节点的坐标表达式如下：

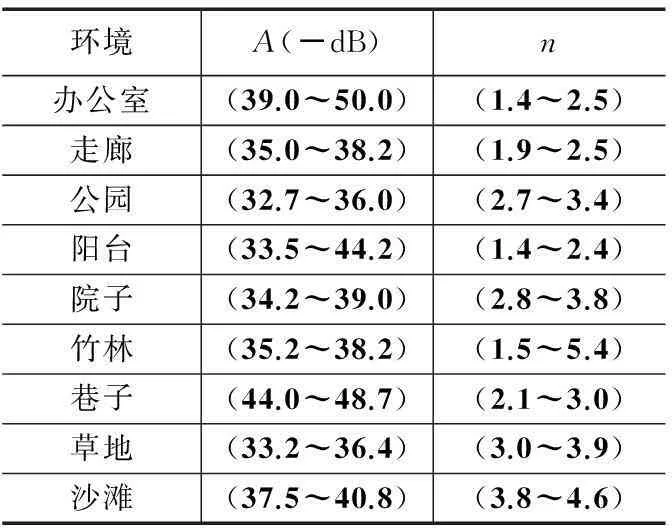
表1　不同情况下A和n值

(5)

也可以简化为式(6)：

(6)

式(6)中，(X,Y,Z)表示未知节点的坐标，(xi,yi,zi)表示信标节点的坐标，k表示能与未知节点进行通信的信标节点个数。

上述质心算法由于并没有考虑信标节点离未知节点的远近程度对未知节点定位的影响，因此定位效果不好，显然信标节点离未知节点越远，对未知节点的影响越小，反之，则对未知节点的影响越大。考虑到这个因素，在质心算法的基础上加一个权值，这个权值与距离成反比，从而可提高定位的精度。加权质心算法[10]的公式如下：

(7)

(8)

式(7)中，(X,Y,Z)表示未知节点的坐标，N表示与未知节点能通信的信标节点的坐标，wi表示信标节点的权重，(xi,yi,zi)表示信标节点的坐标，式(8)中的di表示未知节点与信标节点的距离，也就是公式(4)求得的d，n为权重系数，一般取1~4，这里取1。利用公式(7)求得未知节点的初始坐标，然后再代入泰勒级数展开式中，使节点的定位更加准确。

2.3泰勒级数展开法

泰勒级数Taylor展开法是一种需要初始未知的递归算法，如果初始位置选取不恰当，可能会造成算法不收敛，这里我们选取加权质心算法来定位未知节点的初始位置，然后在利用泰勒级数展开法来更精确地定位未知节点的坐标。由式(7)可知，(X,Y,Z)表示未知节点的坐标，(xi,yi,zi)表示信标节点的坐标，di表示未知节点与信标节点的距离，于是用一个函数fi(X,Y,Z)来表示信标节点与未知节点测量距离和估计距离之间的差值，如式(9)所示：

(9)

假设根据加权质心算法得到未知节点坐标为(X0,Y0,Z0)，把它代入公式(9)的X，Y，Z再将式(9)在(X0,Y0,Z0)点处用泰勒级数展开到一阶导数，忽略后面的高阶项，得到式(10)：

(10)

其中:fi代表fi(X0,Y0,Z0)，当fi(X,Y,Z)足够小时定位的节点就是实际的节点，所以我们令fi(X,Y,Z)=0，式(10)可以写成矩阵的形式，如式(11)：

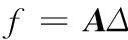
(11)

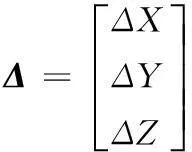
(12)

(13)

(14)

(15)

求解矩阵f=AΔ，其最小二乘解为：

(16)

得到Δ后，修正未知节点的坐标，X=X0+ΔX，Y=Y0+ΔY，Z=Z0+ΔZ重复以上步骤，直到ΔX，ΔY，ΔZ满足预先设定好的值ε，ε=0.001，使得ΔX2+ΔY2+ΔZ2≤ε，记录此时的ΔX，ΔY，ΔZ则未知节点的坐标就为X=X0+ΔX，Y=Y0+ΔY，Z=Z0+ΔZ从而进一步提高了节点的定位精度。

2.4算法流程

加权质心和泰勒级数展开协同定位法是在加权质心算法的基础上更精确定位的一种算法，该算法具有定位精度高，误差小等特点。具体实现步骤如下：

第1步：产生信标节点和未知节点的坐标集。根据实际情况在Matlab中产生信标节点的坐标(xi,yi,zi)与未知节点的坐标(X,Y,Z)。

第2步：确定与未知节点具有通信能力的信标节点坐标。由于在实际环境中RSSI[11]的测量具有不确定性，相同距离的同一个位置所测得RSSI都有很大的区别，所以我们利用公式(2)计算未知节点(X,Y,Z)与信标节点(xi,yi,zi)距离为d时的RSSI，如果RSSI[12]大于所设的限值-90，则认为未知节点在信标节点的通信范围内，记录下此时的信标节点坐标。用于后面的加权质心算法进行计算。

第3步：求出未知节点与能与其通信的信标节点的距离。根据第2步求得的RSSI与公式(4)求得未知节点与信标节点的距离di。

第4步：确定未知节点的初始坐标。把第2步求得的信标节点坐标与第3步求得的未知节点与信标节点的距离di代入公式(7)、(8)求出未知节点的初始坐标。

第5步：确定未知节点的坐标。根据第4步求出的初始坐标代入公式(16)求出修正量ΔX，ΔY，ΔZ的值。在判断是否满足ΔX2+ΔY2+ΔZ2≤ε，如果满足则记录下此时ΔX，ΔY，ΔZ的值，代入公式X=X0+ΔX，Y=Y0+ΔY，Z=Z0+ΔZ得到未知节点的最终坐标，具体流程如图2所示。

图2　定位流程图

3算法仿真与分析

以某办公楼一、二楼为实验场景，办公楼的长为52 m，宽为18 m，层高3 m，二楼的平面如图3所示，●代表信标节点灯的位置，总共15个，＊代表未知灯节点的位置，总共55个，一楼的情况类似。建立直角坐标系，二楼信标节点灯的坐标如下：(1.6，2.3，6)，(14.3，2.3，6)，(26.6，2.3，6)，(38.5，2.3，6)，(47.5，2.3，6)，(1.4，8.5，6)，(13.4，8.5，6)，(25.4，8.5，6)，(31.4，8.5，6)，(46.4，8.5，6)，(1.6，14.3，6)，(14.3，14.3，6)，(26.6，14.3，6)，(38.5，14.3，6)，(47.5，14.3，6)。

图3　二楼平面示意图

为了比较不同定位算法的定位性能，在Matlab环境下进行仿真实验。●代表信标节点的位置，＊代表未知节点的实际位置，ο表示未知节点定位的位置，实际位置与定位位置之间的线段表示定位的误差。加权质心算法和协同定位算法的定位结果分别如图4，图5所示，从图中可以看出加权质心算法定位误差较大，而协同定位算法定位误差较小，完全符合智能照明系统中灯具节点定位精度高的要求。图6为两种算法的定位误差对比图，加权质心算法的最大误差为5.7，平均误差为3.4，协同定位算法的最大定位误差为1.8 m，平均误差为0.7，对比上述结果可以发现协同定位算法的最大定位误差都比加权质心算法的平均定位误差要小，可见，协同定位算法明显提高了定位的精确度，证明了算法的优越性。

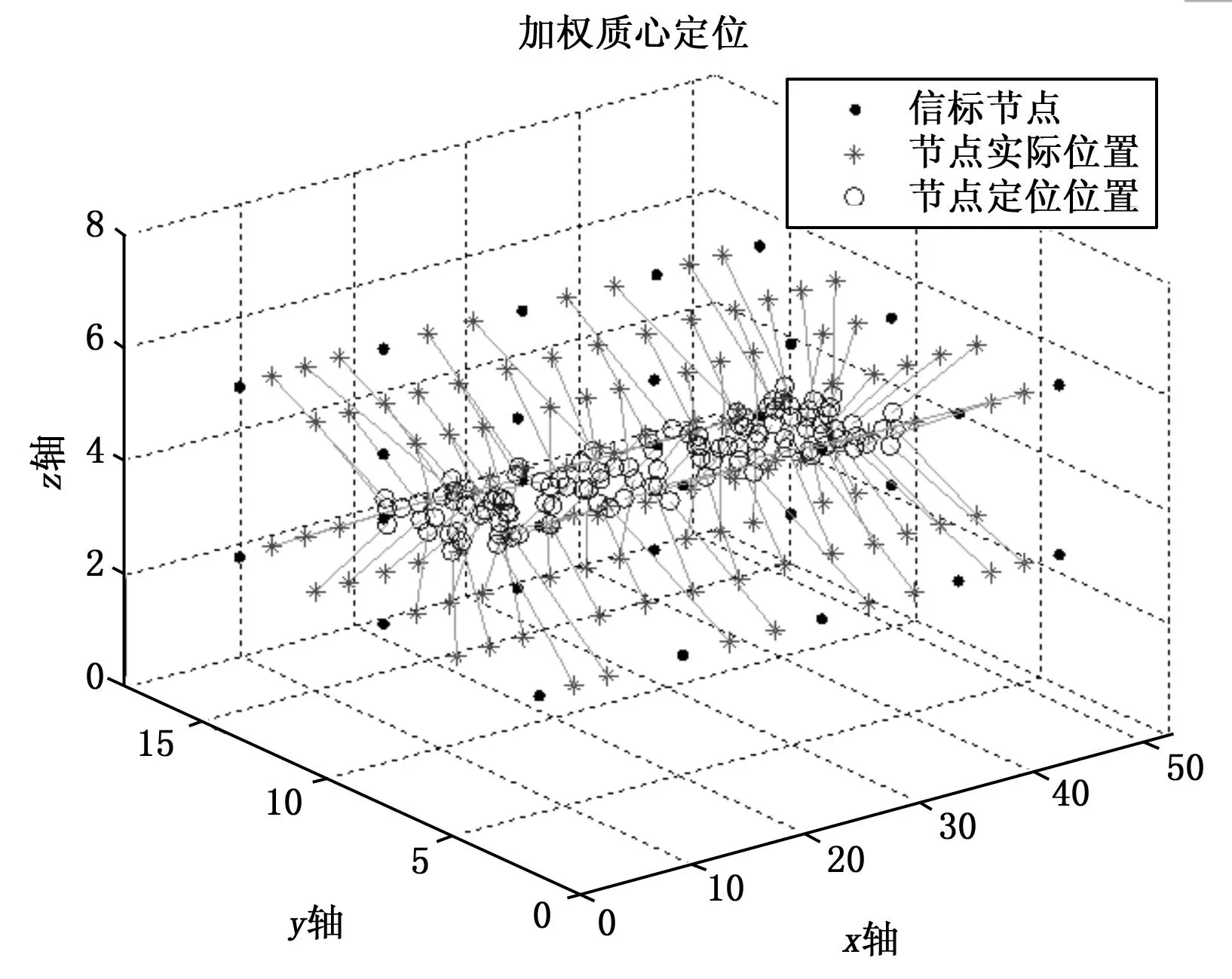
图4　加权质心定位示意图

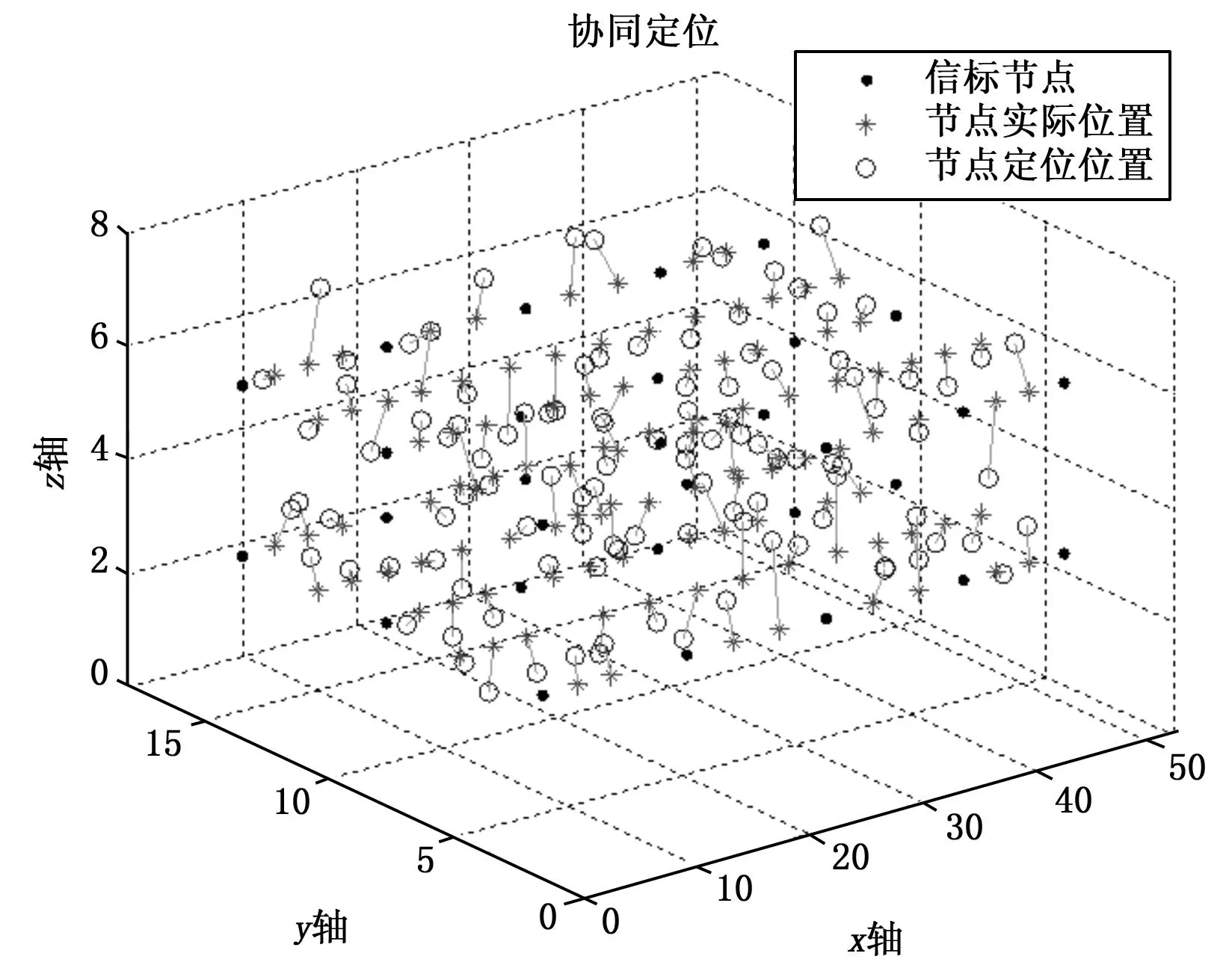
图5　协同定位示意图

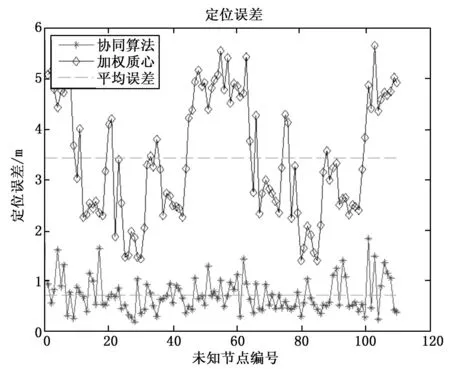
图6　定位误差对比图

4总结

针对无线智能照明系统中灯具的定位问题，提出了一种基于加权质心和泰勒级数展开协同定位的算法。一方面有效改善了泰勒级数算法在初始值偏离真实值较大的情况下算法不收敛的问题；另一方面有效提高了定位的精度。最后通过仿真实验比较了协同定位算法和加权质心算法的定位效果，仿真结果表明：协同定位算法的定位误差明显小于加权质心算法，提高了定位的精度，对于无线智能照明控制系统的定位具有一定的借鉴意义。

参考文献：

[1] 徐勇,栾晓明,王丹.基于ZigBee技术的智能照明系统设计[J].国外电子测量技术,2010,29(1):42-45.

[2] 殷骏,王巍.基于Zigbee的LED智能照明系统设计[J].照明工程学报,2011,22(4):75-78.

[3] 王小平,罗军,沈昌祥.无线传感器网络定位理论和算法[J].计算机研究与发展,2011,48(3):353-363.

[4] 王沁,何杰,张前雄,等.测距误差分级的室内TOA定位算法[J].仪器仪表学报,2011,32(12):2851-2856.

[5] 宫娜娜,王缓缓.无线传感器网络质心算法的最佳通信半径[J].计算机仿真,2013,30(5):203-207.

[6] 王景珲. 一种基于DV-Hop的无线传感器网络节点定位算法[J]. 计算机工程,2015,41(1):82-86.

[7] 戴国华,易灵芝,王根平. 一种新的基于ZigBee技术定位算法[J]. 计算机测量与控制,2012,04:1105-1107.

[8] 朱斌,谭勇,黄江波. 基于ZigBee无线定位技术的安全监测系统设计[J]. 计算机测量与控制,2010，18(6):1247-1249，1252.

[9] 刘玉军,蔡猛,高立恒,等. 基于RSSI测距的传感器节点质心定位修正算法[J]. 计算机测量与控制,2014,22(9):2860-2862.

[10] 王洪元,蒋燕蓉,焦筱悛,等.一种改进的加权质心自定位算法[J].计算机与应用化学,2014,31(3):263-267.

[11] RSSI-Based Indoor Localization and Tracking Using Sigma-Point Kalman Smoothers[J].IEEE Journal of Selected Topics in Signal Processing,2009,3(5):860.

[12] Yaghoubi F, Abbasfar A, Maham B， et al.Energy-Efficient RSSI-Based Localization for Wireless Sensor Networks[J].IEEE communications letters: A publication of the IEEE Communications Society,2014,18(6):973-976.

Application of A Cooperative Localization Algorithm in Intelligent Lighting System

Fu Jundong, Zhang Yin

(School of Electrical and Electronic Engineering，East China Jiaotong University, Nanchang330013,China)

Abstract:Lamps are the controlled object of the intelligent lighting system. However, The premise of controlling the lamps is to find the position. In view of the lamp localization problem, this paper puts forward a kind of cooperative localization algorithm based on weighted centroid and Taylor series expansion, In order to effectively improve the stability and accuracy of localization, in this paper, the weighted centroid algorithm is used to get initial location result which acts as the initial value in Taylor series expansion algorithm to get accuracy results. The Simulation results show that The cooperative localization algorithm is not only good convergence and high precision, compared with the traditional weighted centroid algorithm, maximum position error is less than 1.8 m, the average position error can reach 0.7 m. The localization algorithm is applied to intelligent lighting control system and is advantageous to the accurate control of lamp nodes.

Keywords:intelligent lighting system; node localization; distance measurement; weight centroid; Taylor series expansion

文章编号：1671-4598(2016)02-0279-04

DOI：10.16526/j.cnki.11-4762/tp.2016.02.077

中图分类号：TP312

文献标识码：A

作者简介：傅军栋(1972-)，男，陕西汉中人，硕士，副教授，主要从事无线通信，电力系统，建筑电气及智能化方向的研究。

收稿日期：2015-09-06；修回日期：2015-10-09。