基于摆扫反射镜的大视场成像像移模型

苗　壮，何　斌

(1.中国科学院 长春光学精密机械与物理研究所，长春　130033; 2.中国科学院大学，北京　100049)



基于摆扫反射镜的大视场成像像移模型

苗壮1，2，何斌1

(1.中国科学院 长春光学精密机械与物理研究所，长春130033; 2.中国科学院大学，北京100049)

摘要：为实现大视场技术指标，建立了一种基于摆镜转动的摆扫成像模型;通过对摆扫成像与推扫成像模式的比较，分析得出当横滚角等于摆镜转角的2倍时，摆扫成像能够实现与推扫成像小姿态时相同的视场；经过实验验证，在横滚角为2°、4°、6°、8°、10°时，文章的方法与推扫成像模型像移相对误差在1%以内，偏流角大小相对误差在0.001%以内，两种方法保持了较好的一致性，保证了模型的合理性与正确性;此外，该模型还可以通过实时地控制摆镜的转动来实现穿航方向上的对地的扫描成像，进而实现大视场、宽幅盖对地成像，减小回访周期，提高空间相机对地成像的工作效率。

关键词：大视场;摆扫成像;推扫成像

0引言

随着空间相机的发展，其对地成像的需求不断增加，大视场空间相机已成为遥感领域研究的重点和热点。增大视场可以获得高质量宽幅盖的地面图像，减小相机的回访周期，大大提高空间相机的工作效率[1],而增大视场通常会使遥感器质量和体积的增加，导致成本的巨额增长。如何在获得大视场指标的同时兼有轻小型化结构是当下空间相机设计权衡的指标[2-3]。国内方面，有人提出侧摆成像[4]以实现对地扫描的大视场成像，但现有的技术表明，在轨运行的空间相机还只能进行小角度的侧摆和俯仰，达不到所谓的大视场成像的技术指标。同时高分辨率空间相机与姿态角的配合度也很低，大大降低了相机成像灵敏度，而且相机的机动成像过程控制起来比较困难。因此，本文提出一种基于摆镜转动的摆扫成像方式来代替推扫成像，以实现对地成像过程的大视场成像。

空间相机对地成像过程中，卫星平台的轨道运动、姿态变化、摆扫反射镜的摆动以及地球自转运动，形成相机像面的像移速度矢量。为了保持空间相机像面与地物相对静止，需要进行像移匹配。早在2000年，王家骐等人就对像移相关问题进行了研究，基于坐标变换理论建立了星下点像移速度矢量模型，并成为国内像移速度模型经典解法[5]；2009年仲惟超等人针对卫星姿态建立了基于矢量的像移模型，该模型不但适用于星下点成像，还可用于侧摆和俯仰同时存在时的像移分析，但是只适用于侧摆和俯仰在小角度变化时的情况[6]；2013年，张媛等人基于45°反射镜建立的侧摆成像像移速度模型，实现对卫星当前轨道所在地面投影区域的某一侧进行推扫，增大了视场的探测角度，但是并未实现对地投影过程中将星下点与投影区域的两侧同时扫描成像，增加了相机的回访周期[4]；2014年杨飞等人提出了一种光线追迹摆扫成像像移模型，但该模型适用于通过整机的滚动来实现对地摆扫成像，相比于摆镜转动成像，其控制过程更加的困难与复杂[7]。本文在坐标变换的基础上用矩阵分析方法，结合摆镜旋转矩阵建立摆扫成像像移匹配模型，该模型能够实现在相机沿着轨道飞行的过程中，通过摆镜的实时转动，实现大视场、宽幅盖对地成像。

1空间TDICCD相机摆扫成像模式

空间相机对地摆扫成像[8]模式如图1所示，光轴经过摆镜反射后指向地面景物点，通过摆镜的转动，光轴对地指向发生变化，以此实现对地成像过程中的大视场扫描成像。

由光学反射定律知，入射光线不变，反射镜转动ξ，则出射光线转过2ξ。

如图1，当摆镜转过ωxt，光轴对地指向改变2ωxt；推扫成像[9]过程中，通过改变卫星的姿态角，实现对星下点的某侧进行扫描成像。当相机绕着横滚轴转动φ时，光轴由原先指向星下点的位置转动了φ，实现侧摆成像。从图1和图2比较可知，当相机的横滚角φ等于摆镜的转角2倍，即2ωxt时，光轴的改变的角度相等，即可以通过改变摆镜转动的角度来实现和相机的机动成像的等同视场效果。

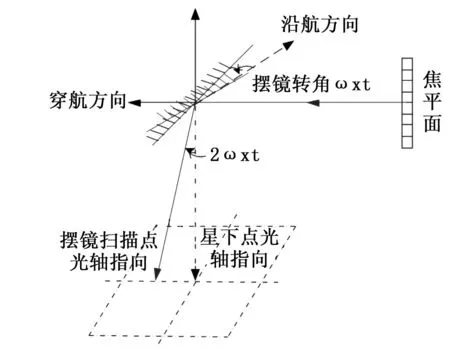
图1　摆扫成像示意图

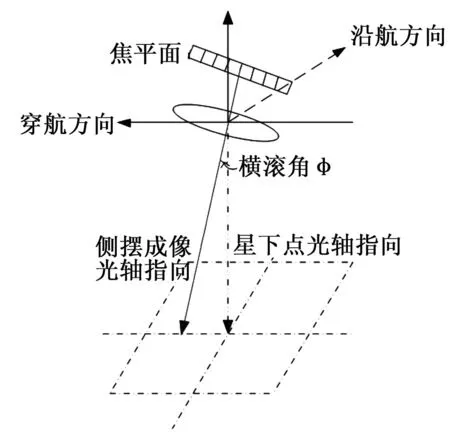
图2　推扫成像示意图

2摆扫成像像移速度矢量推导

根据摆扫成像的工作方式，利用齐次坐标变换[5]计算地面景物到相面的坐标变换。如图3所示，其中的各坐标系定义如下(均采用右手坐标系)：

图3　坐标变换示意图

景物地理坐标系G(G1,G2,G3)：G系原点为光轴指向的地面景物点，G3轴的指向为光轴指向相机方向，G1轴与卫星轨道前进方向相同；

光轴景物地心坐标系K(K1,K2,K3)：其原点与地心重合，K3轴指向相机光轴指向的景物点，K1轴与过K3轴垂直于轨道面的平面相垂直，指向卫星轨道前进方向。将G系绕着G1轴旋转摆镜转角以及地心角后，再沿着G3平移-R，得到光轴景物坐标系；

地心惯性坐标系I(I1,I2,I3)：原点与地心重合，I2轴指向地球北极，I3轴指向卫星的轨道平面与赤道的降交点；

地球坐标系E(E1,E2,E3)：坐标系固连于地球，原点与I系的原点重合，E2指向北极，地球坐标系在I系内逆时针方向以角速度ω绕E2轴转动；

卫星轨道坐标系B(B1,B2,B3)：原点在轨道上，B1轴指向轨道切向，B3轴指向天顶，B2与轨道面垂直，B系在I系内，沿着飞行轨道以角速度Ω进行轨道运动；

卫星坐标系S(S1,S2,S3)：该坐标系原点与轨道坐标系原点重合，卫星无姿态时两个坐标系重合，卫星的三轴姿态φ,θ,ψ是指S系在B系中的三轴姿态，欧拉姿态角转序为123；

摆镜坐标系M(M1,M2,M3)：初始时刻，卫星坐标系绕着S1旋转45°(为便于计算，将初始时刻设为45°)，即为摆镜初始坐标系。摆镜扫描时，摆镜坐标系绕着M1以角速度ωx进行摆动；

相机坐标系C(C1,C2,C3)：相机物镜的主点为该坐标系的原点，当相机在卫星内无安装误差或者很小时，相机与卫星坐标系可以认为是重合的，比例尺缩小f/L倍；

像面坐标系P(P1,P2,P3)：坐标系原点在像面中心，C系沿C2轴平移f，P1,P3与C1,C3反向后即得到P系，P1,P3组成像面。

由坐标系的定义知，地面景物坐标系到像面坐标的变换关系如下：

图4　坐标变换过程示意图

(其中：X→Y的坐标系变换过程中,Ri[ε]表示绕着Xi旋转ε,Ti[ρ]表示沿着Xi平移ρ，Si[δ] 表示缩放δ)。由此可得目标点坐标到像点坐标的变换关系如式(1)所示：

(1)

其中:

γ2=arcsin(L0sin(-2ωxt)/R)

K为地坐标系到地心惯性坐标系的变换矩阵：

M为摆镜扫描矩阵。摆扫成像过程：景物首先经过光学系统，然后经过扫描变换矩阵进入扫描镜动坐标系，由反射镜矩阵进行反射，再由扫描变换矩阵的逆矩阵转换到静坐标系中，获得出射矢量，由光学反射矢量[10]以及摆镜坐标系的定义知，摆镜初始时刻法线矢量为：

反射镜矩阵为：

所以摆镜旋转矩阵为：

像面位置方程

(2)

将式(1)两边对时间t微分后，求出t=0的值，即可得到像面上各点的像移速度方程：

式中,VP1,VP3分别为相机像面的前向像移速度和横向像移速度，其合速度(像移速度矢量模值)为：

(3)

偏流角(像移速度方向)为：

(4)

3实验结果与分析

由式(1)知，当横滚角度φ=2ωxt=0°时，该模型即为星下点成像像移模型，只是由于摆扫反射镜的存在，横向像移由P2变为P3，前向像移仍为P1。为进一步验证本文建立的摆扫成像模型的合理性与可靠性，参考XX型号空间相机成像参数，将其带入到该模型中进行仿真并与推扫成像模型(小姿态侧摆成像)所得试验结果进行对比。

设定相机在轨参数如下：轨道倾角i0=100.5°，相机焦距2m，轨道高度1 200km，卫星下行，摆镜转角分别为1°、2°、3°、4°、5°，即侧摆成像[11]时横滚角度为2°、4°、6°、8°、10°时，计算出焦平面的像移位置以及偏流角。当摆扫成像时，摆镜转角改变，但此时的横滚角度设置为0°。通过实验可得表1、图6和图7，其中表1为不同摆动摆镜转角下的像面位置以及偏流角，图6和图7分别为不同摆镜转角下的摆扫成像模型与推扫成像模型的像面位置以及偏流角大小的比较。

由表1可知，摆镜的转角只对穿航方向的像移产生影响，随着转角的增加，穿航方向的分量增大，而沿航方向无变化，这与侧摆成像过程中的变化一致，即摆镜转角/横滚角只对穿航方向的像移产生影响而对沿航方向的像移没有影响。

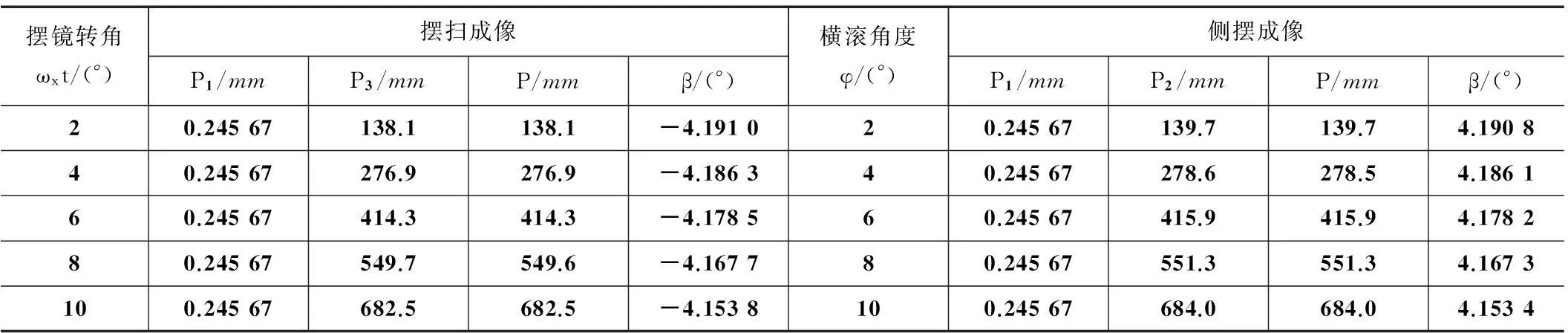
表1　不同摆动摆镜转角/横滚角下的像面位置以及偏流角

图5　不同摆镜转角下的像面位置

图6　不同摆镜转角下的偏流角

由图5、图6可知，当横滚角度为小姿态角(2°~10°)时，本文的方法与侧摆成像模型的像移和偏流角基本相等，由表1计算知，像移相对误差在1%以内，偏流角大小相对误差在0.001%以内，两种方法保持了较好的一致性，完全满足像移补偿的要求，证明了该模型在小姿态下的合理性与正确性。相比于卫星平台的姿态控制，摆镜的转动控制较为简单与容易，该模型能够通过改变摆镜的转角，实现与小姿态成像的等同效果。

此外，该模型还可以通过对摆镜角速度的实时控制，实现穿航方向上的扫描成像。当摆镜角速度为3°/s时，光轴的转动速度为6°/s(目前的姿态角速度仅为1°/s),在轨高度为1 200km时，光轴扫过的地面景物的速度

V3=(6*3.14/180)*1 200 km/s=125.6 km/s

飞行器对应的星下点速度

由于地球自转产生的地面像移速度在沿航方向的分量

V2∥=ω·R·cos(180°-100.5°)=0.085 km/s

穿航方向上的分量V2⊥=ω·R·sin(180°-100.5°)=0.46km/s所以沿航方向的合速度

Vx=V1+V2∥=6.185 km/s

穿航方向像移速度

Vy=V3+V2⊥=126.06 km/s

由图7可知，由卫星运动，地球自转，摆镜转动导致地面景物移动速度在穿航方向上式沿航方向上的21倍，即当卫星沿着轨道飞行1m时，可以通过摆镜转动实现穿航方向上幅宽21m的扫描成像，通过对CCD进行合理拼接，可以保证相邻扫描线之间在星下点不漏扫，不大部分重叠。

图7摆扫成像地面景物移动速度

为保证星下点不漏扫，不大部分重叠，可以采用单向摆动或者转动扫描，图8为单向摆动式对地扫描成像的地面图形，从图中可知，相邻两次扫描成像之间条带方向一致，保证了一定的重叠率，确保了对地成像过程中星下点不漏扫，不大部分重叠。

图8摆扫成像扫描地面图形(单向摆动)

4结论

在坐标变换的基础上用矩阵分析方法，结合摆镜旋转矩阵建立摆扫成像像移匹配模型。该模型在小姿态角度(横滚角度≤10°)，即横滚角φ分别等于2°、4°、6°、8°，10°条件下，与推扫成像模型相比像移相对误差在1%以内，偏流角大小相对误差小于0.001%，两种方法保持了较好的一致性，完全满足像移补偿的要求，同时还能够实现与大姿态角度成像的相同视场，证明了该模型的正确性。此外通过对摆镜转动进行实时控制，实现了对地成像过程中的大视场、宽幅盖成像，减少回访周期，提高空间相机对地成像的工作效率。作为大视场空间相机成像像移补偿的一种计算方法，对工程应用具有一定的指导意义。

参考文献：

[1] 薛庆生，黄煜，林冠宇.大视场高分辨力星载成像光谱仪光学系统设计[J].光学学报，2011,31(8)1-6.

[2] 杨秉新.TDICCD相机的相对孔径与器件像元尺寸关系的研究[J].航天返回与遥感，2001,22(2):9-12.

[3] 芮涛.大口径长焦距扫描成像光学系统像质研究[D]. 哈尔滨：哈尔滨工业大学，2012.

[4] 张媛.星载TDICCD相机侧摆成像像移速度建模与分析[D]. 哈尔滨：哈尔滨工业大学，2013.

[5] 王家骐,于平，颜昌翔.航天光学遥感器像移速度矢计算数学模型[J]. 光学学报，2004,24(12)：1585-1589.

[6] 仲惟超.航天器轨道姿态和姿态参数对光学成像的影响[D]. 哈尔滨：哈尔滨工业大学，2009.

[7] 杨飞，金光，曲宏松.航天时间延迟积分CCD相机摆扫成像快速几何校正设计与分析[J].光学学报，2014,34(1)：0111001-1-0111001-7.

[8]https://en.wikipedia.org/wiki/Whisk_broom_scanner.

[9]https://en.wikipedia.org/wiki/Push_broom_scanner.

[10] 陈世平.空间相机设计与实验[M].北京：中国宇航出版社，2009.

[11] 程少园，张丽，高卫军，等.大视场空间相机侧摆成像时几何参数模型[J].红外与激光工程，2015,44(6)：1872-1877.

Image Motion Model of Large Field of View Imaging Based on Swing Mirror

Miao Zhuang1,2,He Bin1

(1.Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, Changchun130033, China；2.University of Chinese Academy of Sciences, Beijing100049, China)

Abstract:To achieve the large field of view, it establishes the whiskbroom imaging model based on the rotating mirror.Comparing the whiskbroom and pushbroom models, it finds that when the roll angle is two times of the angle of the swing mirror, the pushbroom and whiskbroom has the same field of view. Through the experimental verification, at the small angle attitude 2°、4°、6°、8°、10°，the relative error of this model is within 1% and relative error of drift angle is within 0.001% of the pushbroom imaging model. Two ways have good consistency, ensuring the rationality and accuracy of the model. Besides, the model can scan imaging across the navigation direction by controlling the rotation of the swing mirror in real time to realize large field of view, wide swath of imaging, reducing the return period and improving the working efficiency of the space camera.

Keywords:large field of view；whiskbroom imaging；pushbroom imaging

文章编号：1671-4598(2016)02-0242-05

DOI：10.16526/j.cnki.11-4762/tp.2016.02.067

中图分类号：TP701

文献标识码：A

作者简介：苗壮(1990-)，男，吉林桦甸人，硕士研究生，主要从事遥感成像方向的研究。

基金项目：国家863高技术研究发展计划资助项目(863-2-5-1-13B)。

收稿日期：2015-08-24；修回日期：2015-09-16。

何斌(1961-)男，吉林长春市人，研究员，博士生导师，主要从事光学遥感相机CCD成像驱动电路设计方向的研究。